Обыкновенные дифференциальные уравнения. Документ Microsoft Word. 1 Определение ряда Фурье 2Ппериодических функций. Вывод коэффициентов Фурье
 Скачать 45.8 Kb. Скачать 45.8 Kb.
|
|
1) Определение ряда Фурье 2П-периодических функций. Вывод коэффициентов Фурье. Тригонометрическим рядом, называется функциональный ряд вида 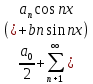 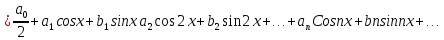 Где действительные числа 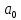 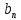 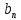 (n=1,2,…) называется коэффициентами (n=1,2,…) называется коэффициентамиПусть 2п-периодическая функция f(x) такова что представляется тригонометрическим рядом сзодится если в данной функции [-п;п], т.е. является суммой ряда :  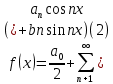 Чтобы найти равенство 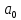 проинтегрируем равенство (2) на отрезке [-п;п] проинтегрируем равенство (2) на отрезке [-п;п]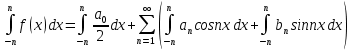 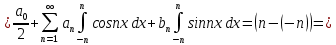 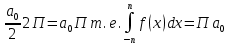 Откуда 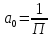 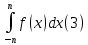 Чтобы найти коэффициент 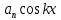 (к (к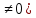 [-п;п] [-п;п]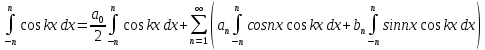 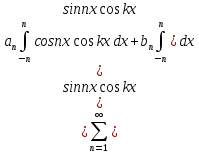 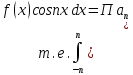 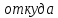 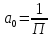 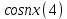 Чтобы найти коэффициент умножаем левые и правые части (2) на sinkx на sin=0и интегрируем по [-п;п] ………………………. 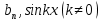 [-п;п] [-п;п]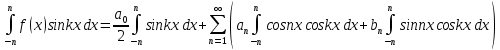 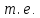 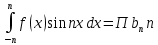 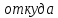 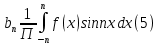 О. Рядом Фурье для 2п периодической функции у=f(x) называется выражение вида: 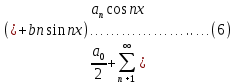 где 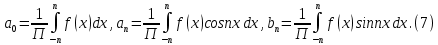 (7)-коэффициент ряда Фурье для функции y=f(x) 2. Теорема Дирихле. Теорема (Дирехле): Пусть 2п периодическая функция f(x) [-п;п] удовлетворяет двум условиям -f(x) кусочно-монотонна на [-п;п], т.е монотонна на вс 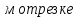 или отрезок можно разбить на конечное число интервалов так, что на каждом из них функция монотонная или отрезок можно разбить на конечное число интервалов так, что на каждом из них функция монотонная -f(x) кусочно-непрерывна, т.е. непрерывна или имеет конечное число первого рода Тогда ряд Фурье функции f(x) сходится к функции f(x) на этом отрезке и при этом: 1. Сумма полученного ряда S(x) равна значению функции f(x)в точках непрерывности функции т.е. S(x)= f(x) 2. В каждой x=x0 разрыва функции f(x) сумма ряда равна 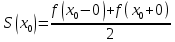 3.В точках х=-П и х=П сумма ряда равна S(-п)=S(п)= 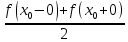 3. Разложение в ряд Фурье четных и нечетных 2П-периодических функций. Если функция f(x) = является 2п-периодической функцией и удовлетворяет условиям торимы Дирехле то для нее можно построить ряд Фурье f(x) 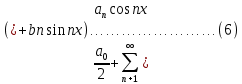 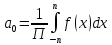 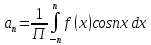 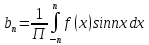 Если f(x) нечетная функция то 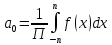 интервал от нечетной функции по сем. отрицат. интервал от нечетной функции по сем. отрицат.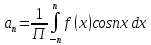 (7) (7)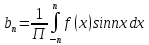 = =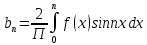 .(8) .(8)Тогда для ряда Фурье нечетной функции будет следующим 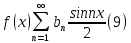 Где коэффициент 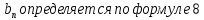 (9)- разложение ряда Фурье по sin Если f(x) нечетная 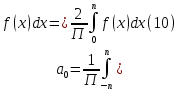 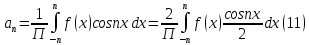 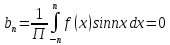 Ряд Фурье для четной функции имеет вид 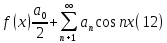 Где 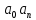 определяется по формуле 10 и 11, где 12 разложение функции по cosx определяется по формуле 10 и 11, где 12 разложение функции по cosx4. Разложение в ряд Фурье функций произвольного периода. Пусть функция f(x) периодическая с произвольным периодом 2l Найдем разложение в ряд Фурье для этой функции. Сделаем замену: 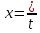 Тогда 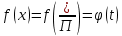 Если х=-l То t= 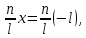 То 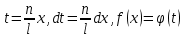 Таким образом при данной замене [-l;l] переходит в [-п;п] Т.о. нововведённая функция 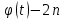 периодическая след. Для нее сложно разложить Ряд Фурье периодическая след. Для нее сложно разложить Ряд Фурье 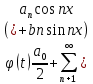 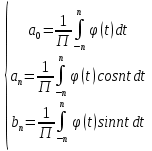 Возвратимся к переменной х Если х= 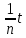 подставим в ряд Фурье и форм. Коэф. подставим в ряд Фурье и форм. Коэф.То t= 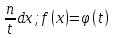  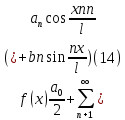 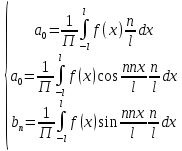 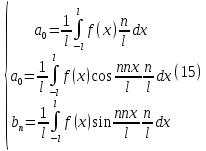 Рядом Фурье для 2l-периодической функции имеет вид (14) коэффициент определяются по формуле (15) 5. Разложение в ряд Фурье четных и нечетных функций произвольного периода. Если f(x) четное, то ряд Фурье будет иметь вид: 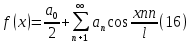 Где коэффициенты вычисляются п формуле 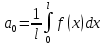 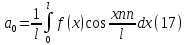 Если f(x) –нечетная функция 2l-периодичская функция то ряд Фурье имеет следующий вид 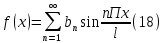 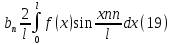 1. Определения дифференциального уравнения 1-го порядка. Начальные условия. Общее и частное решения дифференциального уравнения 1-го порядка. Задача Коши. Дифференциальным уравнениям 1-го порядка называется уравнения связывающего Называющую переменную x искомую функцию y и ее производную у' 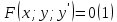 1- Дифференциальные уравнения 1-го порядка в неявном виде О. Если дифференциальное уравнение 1 выразить производную y' то получем дифференциальное уравнение 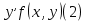 2 - дифференциальное уравнение разрешенная относительно производной О. Условия состоящее в том, что значение x = x0 нулевое соответствует значение y=y0 называется начальным условием Об. y(x0)= y0 (3) Общим решением дифференциального уравнения (1) называется функция φ(x;c) C=const Удовлетворяющее условием а) При подстановке в дифференциальное уравнение превращает его в тождество б) Каково бы не было начальное условия (3) можно найти такое значение константы С=С*, что функция φ=φ(x; С*) является решение уравнения (1) О.Частным решением дифференциального уравнения 1 называется функция φ=φ(x; С*) получаемая из общего решение этого дифференциального уравнения φ=φ(x; С) при конкретном значении const C=C* О. Задач Каши для дифференциального уравнения (1) называется задача нахождения частного решения этого дифференциального уравнения при заданном начальном условии (3): 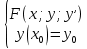 Теорема (Существования и единственность решения задачи Коши) Если в дифференциальном уравнение y'=f(x;y) функция f(x;y) и ее частная производная. 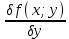 непрерывно в любой области D принадлежащий плоскости Оху то для любой точки непрерывно в любой области D принадлежащий плоскости Оху то для любой точки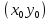 существует единственное решение задачи Каши удовлетворяющее начальному условию существует единственное решение задачи Каши удовлетворяющее начальному условию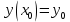 Решение дифференциального уравнения 1 записаны виде 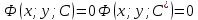 называется общим и частным интегралами соответственно называется общим и частным интегралами соответственноУравнение в дифференциалах Рассмотрим дифференциальные уравнения 1-го порядка разрешен относительно производной 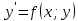 Как известно Как известно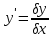 Подставляем в данное уравнение, получаем. Подставляем в данное уравнение, получаем.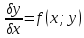 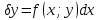 (4)- Частным случаем дифференциального уравнения 1-го порядка в дифференциалах 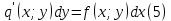 (5)- Уравнение в дифференциалах в общем видите 2. Определение и решение дифференциального уравнения 1-го порядка с разделяющимися переменными. Дифференциальные уравнения 1-го порядка вида 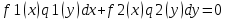 Называется уравнение с разделяющимися переменными Чтобы найти решение данного уравнения надо разделить переменные(около дифференциала dx собрать функцию от x около dy Собрать функцию от y) q делим на произ-е 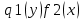 получаем получаем 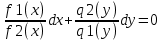 - уравнение с разделяющими переменными 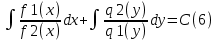 (6) общий интеграл решения дифференциального уравнения с разделяющими переменными 3. Определение однородной функций к-го измерения, 0-го измерения. Функция f(x;y) называется однородной функцией k-го измерения относительно переменных (х;у) если для любого t выполняется равенство 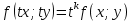 4. Определение и решение однородного дифференциального уравнения 1-го порядка. О. ДУ 1-го порядка 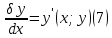 Называется однородным относительно переменных х и у если функция f(x;y) является однородной нулевого измерения относительно x и y Решение однородного ДУ Пусть функция f(x;y) является однородным измерением, то есть по определению выполняется равенство 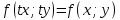 Заменено t=1/x 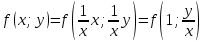 Т.е получили функцию зависящую от отношения 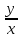 таким образом однородное ДУ можно записать в виде таким образом однородное ДУ можно записать в виде 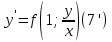 Делаем замену u= 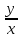 Следовательно y=u*x, y’=u+u’y Подставим в (7’) u+u’y=f(1;u)-u 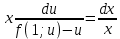 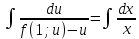 Возвращаемся к переменным ху по формуле, т.е. вместо u везде подставляем 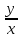 5. Определение линейного дифференциального уравнения 1-го порядка. Решение его методом Бернулли. Линейным ДУ 1-го порядка называется ДУ вида 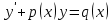 Решение ЛДУ 1-го порядка методом Бернули Пусть дано 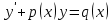 В основе метода Бернули лежит замена искомой функции у произведе. u на v т.е. y=uv, где функция u=u(x) и v=v(x) Найдем y’ 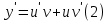 Подставим в ЛДУ 1-го прядка 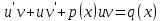 Группируем 2 и 3 слагаемое 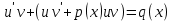 Выносим общий множитель u за скобку 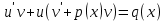 Функции u и v будем искать из системы 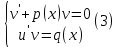 Найдем функцию v 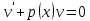 -уравнение разделяющими переменными -уравнение разделяющими переменными 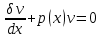 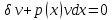 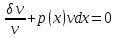 6. Решение линейного дифференциального уравнения 1-го порядка методом Лагранжа. Пусть дано 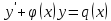 Если 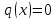 то получаем то получаем 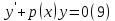 (9)- линейное однородное диф.уравнение 1-го порядка Найдем решение уравнения (9) 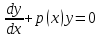 с разделяющими переменными с разделяющими переменными 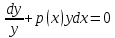 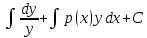 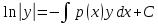 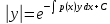 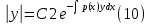 Об. Решением ЛДУ методом Лагранжа будем искать значение конст-у функцией С2=С2(x) Отсюда общее решение из (10) будет иметь вид 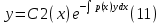 Найдем y’ 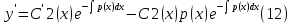 Подставим формулу 11 12 в ЛДУ 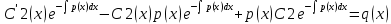 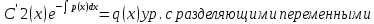 С2(x)- искомая функция 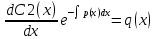 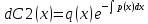 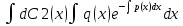 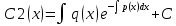 Подставим в формулу 11 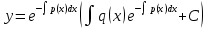 7. Определение и решение уравнения Бернулли. Уравнение Бернули называется дифференциальное уравнение вида 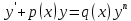 n ∈R n 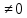 n n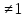 тк 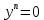 то делим уравнение на то делим уравнение на 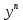 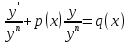 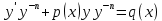 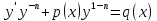 Метод замены z= 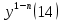 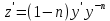 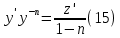 Используя 14 и 15 можно записать диф-ое уравнение с функц. 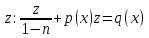 Умнож. 1-n 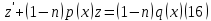 (16)-ЛДУ 1-го порядка можно решить методом Бернули или методом Лагранжа После нахождения функции z необходимо вернуться к функции y по формуле 14 + 8. Определение и решение уравнения в полных дифференциалах. Уравнение в полных дифференциалах P(x;y)dx+Q(x;y)dy=0 называется Уравнение в полных дифференциалах Если левая часть уравнения является полным дифференциалом u(x;y), т.е. 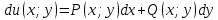 Теорема необходимости и достаточности Условия полного дифференциала функции для того чтобы выражение  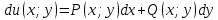 Было дифференциалом некоторой функции необходимо и достаточно чтобы выполнялось равенство 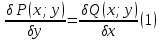 Причем функция P(x;y); Q(x;y) и произв. 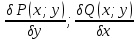 Непрерывна в области D на Оху Доказательство Н: Пусть функция 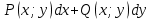 является полным дифференциалом некоторой функции u(x;y) т.е. является полным дифференциалом некоторой функции u(x;y) т.е.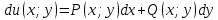 по определению по определению 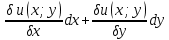 При оформлении получается 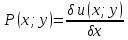 ; ; 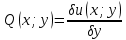 (2) (2)Первую формулу (2) дифференцируем по переменной y; 2-ую формулу дифференцируем по х получаем: 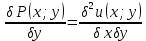 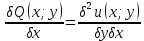 По теореме Шварца смешанные произведения 2-го порядка непрерывной функции равны, т.е. 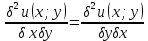 Если равны правые части, то равны и левые 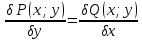 Докажем что существует функция u(x;y) такая что 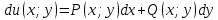 Имеет место формулы (2) 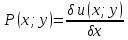 ; ; 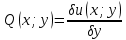 Из первого равенства U(x;y)= 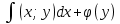 (3) (3)Найдем функцию φ(y) 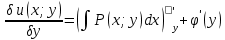 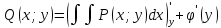 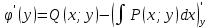 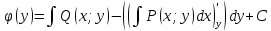 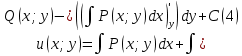 (4)-искомая функция Проверим что полный дифференциал равен выражению 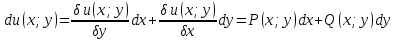 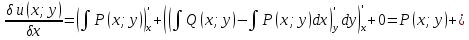 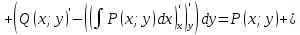 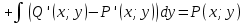 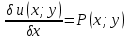 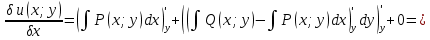 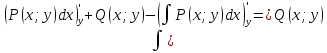 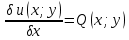 Т.е. полный дифференциал 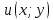 равен выражению равен выражению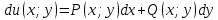 ЧТД Уравнение в полных дифференциалах имеет вид 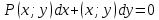 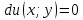 U(x;y)=C (6) C=const (6)-общий интеграл уравнения в полных дифференциалах 9. Интегрирующие множители. Интегшрирующий множитешль Если уравнение P(x,y)dx+Q(x,y)dy=0 не является уравнением в полных дифференциалах то не выполняется равенство 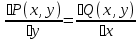 Можно найти множитель функции t(x,y) которая называется интегрирующим множителем при котором уравнение t(x, y)P(x, y)dx + t(x, y)Q(x, y) dy = 0 (7) уравнение будет выполнятся в полных дифференциалах при этом будет выполнятся равенство 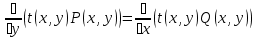 найдем множитель t(xy) воспользуемся формулой производная от произведения получим 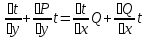 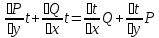 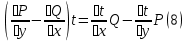 Уравнение 8 является уравнением в частных производных трудноразрешима поэтому сделаем допущение при которых t найти легче: Пусть t=t(x) есть функция от х тогда уравнение 8 будет иметь вид 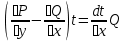 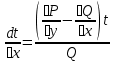 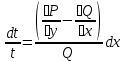 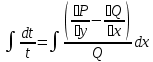 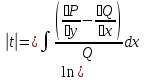 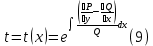 (9)- формула нахождения интегрирующего множителя, зависящего от х, где 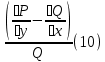 где (10) должна зависеть от х, (условия существования интегрирующего множителя) Пусть интегрирующий множитель t=t(y) Из формулы 8 получаем 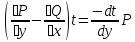 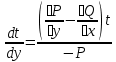 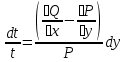 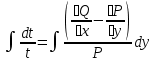 Интегрируем 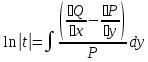 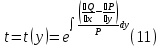 11- формула нахождения интегрирующего множителя, зависящего от y, где 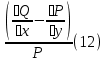 (12) должна зависеть от y Если интегрирующий множитель найден, данное уравнение умножается на него, проверяется условие уравнение в полных дифференциалах, если условие выполняется, то решаем методом, указанным ранее, если условии не выполняется, то ищем ошибку 10. Определение и решение уравнения Лагранжа. Особым решением дифференциального уравнения называется такое решение, во всех точках которого условие единственности не выполняется, т.е. любой окрестности каждой точки с координатами х, у особого решения существуют по крайней мере две интегральные прямые проходящие через эту точку (интегральные кривые –это графики решения ДУ) Особые решения не получаются из общего ДУ не при каких значениях производной константа С ( в том числе С= +-∞) Особым решением является огибающая семейства интегральных кривых, т.е. линия которая в каждой своей точке касается по меньшей мере одной интегральной прямой Уравнение вида 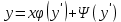 Где φ и Ψ известная функция о производной 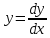 ? Называется уравнение Лагранжа ? Называется уравнение Лагранжа Чтобы решить уравнение Лагранжа вводят параметр p=y’ подставляем в уравнение Лагранжа получаем: 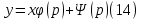 Дифференцируем уравнение (14) по переменной х: 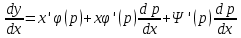 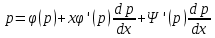 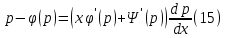 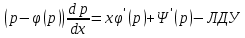 Относительно функции x=x(p) Решаем это ЛДУ методом Бернули или Лагранжа , получаем решение 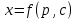 пусть получили общее решение в таком виде пусть получили общее решение в таком виде Общее решение уравнения Лагранжа в параметрическом виде будет следующим 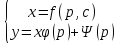 Или 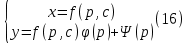 В некоторых примерах общее решение можно записать в явном или не явном виде Когда мы поделили на 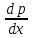 могут быть потеряны корни могут быть потеряны корни 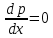 Из уравнения (15) это корни уравнения p-f(p)=0 Пусть P0 корень уравнения полученного из (15) формулы Подставляем корень в (14) получам: 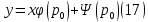 (17)- Особое решение уравнения Лагранжа 11. Определение и решение уравнения Клеро. Уравнение Клеро является частным случаем уравнения Лагранжа, когда 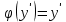 ДУ вида 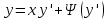 , где , где 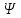 -известная функция от проиводной y’ называется уравнение Клеро -известная функция от проиводной y’ называется уравнение Клеро Чтобы решить уравнение Клеро делаем замену y’=p подставляем в уравнение Клеро получаем: 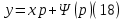 Дифференц. Уравнение (18) 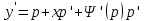 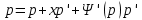 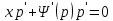 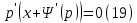 (19) – произведение двух функций ( 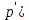 и и 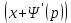 ( произведение =0 если хотябы одни из множителей =0) ( произведение =0 если хотябы одни из множителей =0)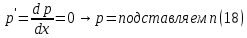 Из (18) 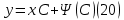 (20)- общее решение уравнение Клеро Приравниваем второй множитель из уравнения (19) к нулю: 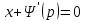 Получаем решение ДУ в параметрическом виде: 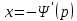 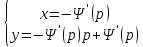 (21)- особое решение уравнение Клеро в параметрической форме |
