Метод стрельбы. НКЗ м. 1. Построение разностной схемы для краевой задачи для линейного оду второго порядка
 Скачать 252 Kb.
|
|
1. Построение разностной схемы для краевой задачи для линейного оду второго порядка Краевую задачу записывают в символическом виде  ,где  - заданный дифференциальный оператор,  - заданная правая часть (см. Годунов С.К., Рябенький В.С. Разностные схемы, с. 82).Разностную схему по аналогии записывают в символическом виде:  ,где  - разностный оператор (см. там же, с. 88).Оператор включает в себя краевые условия и уравнения. Порядок аппроксимации для задачи определяется как минимальный для всех. Рассмотрим краевую задачу для обыкновенного дифференциального уравнения второго порядка (линейного) из упражнения а), с. 89-90 [В.Л. Котов Задания и упражнения по численным методам]:  ,  ,  ,  Запишем дифференциальный оператор и правую часть задачи: 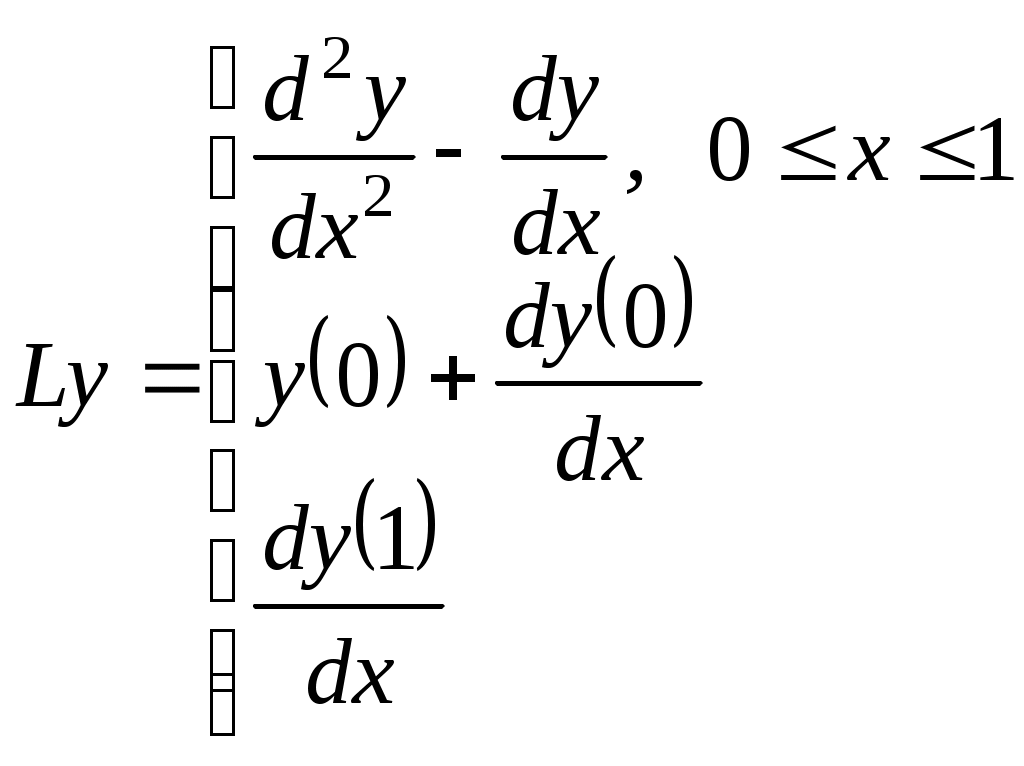  Запишем для полученной разностной схемы разностный оператор и правую часть: 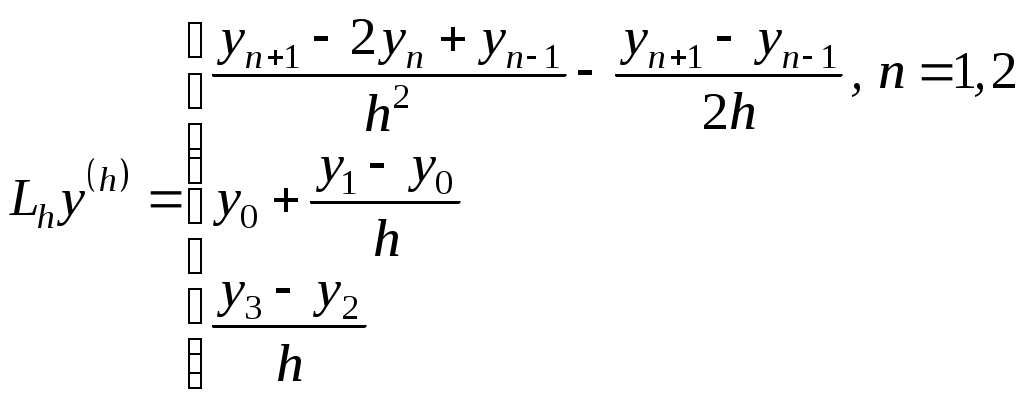 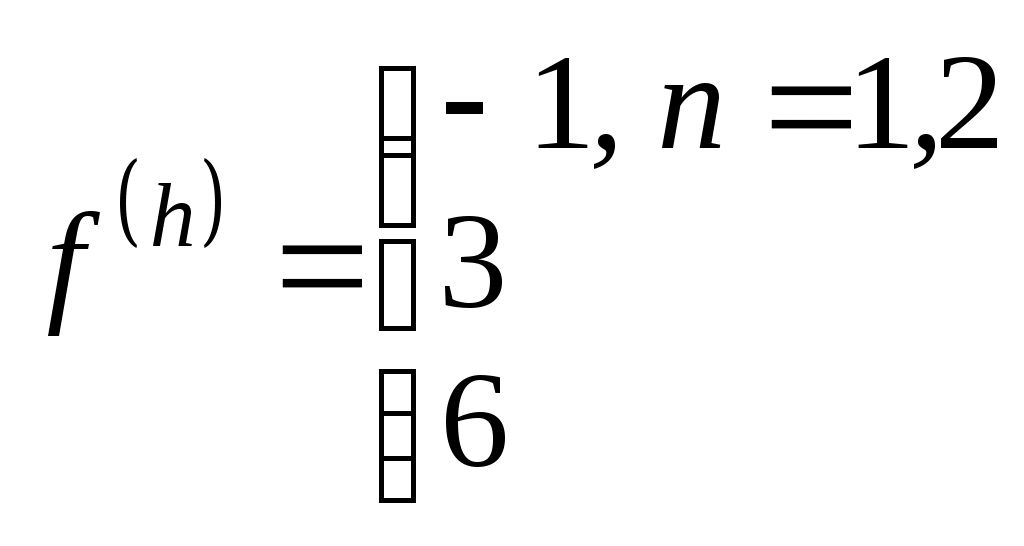 Аппроксимация дифференциального уравнения выполнена со вторым порядком точности. Аппроксимация краевых условий выполнена с первым порядком точности, т.к. для производной использовался шаблон с первым порядком аппроксимации. Следовательно, разностная схема имеет первый порядок аппроксимации. Ответ: построена разностная схема первого порядка аппроксимации. Получена система линейных алгебраических уравнений с трехдиагональной матрицей, для решения которой не применим метод прогонки. Рассмотрим краевую задачу для обыкновенного дифференциального уравнения второго порядка (линейного) из упражнения б), с. 90-91 [В.Л. Котов Задания и упражнения по численным методам]:  ,  ,  ,  Запишем дифференциальный оператор и правую часть задачи: 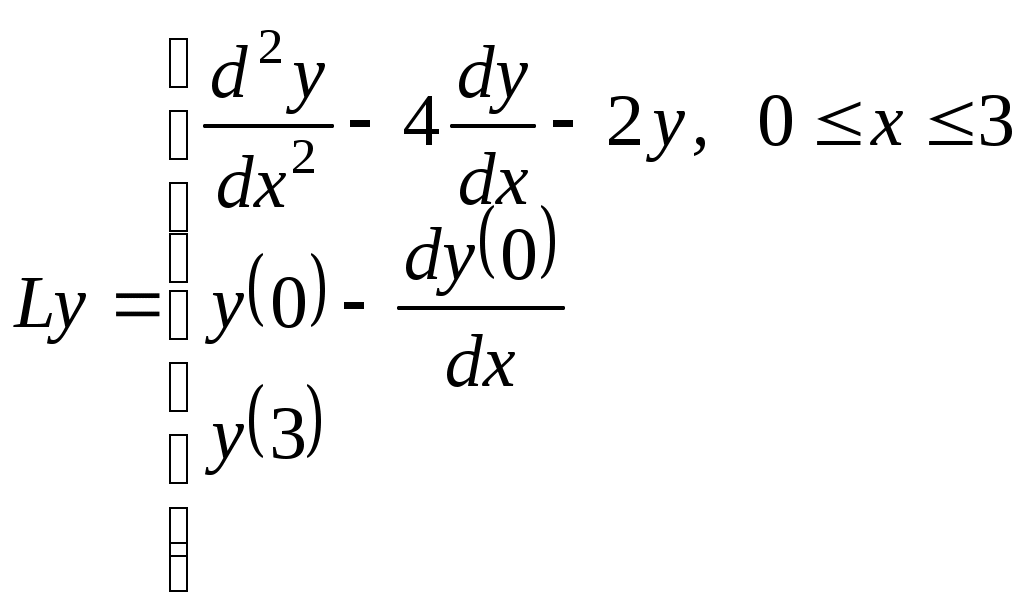  Запишем для полученной разностной схемы разностный оператор: 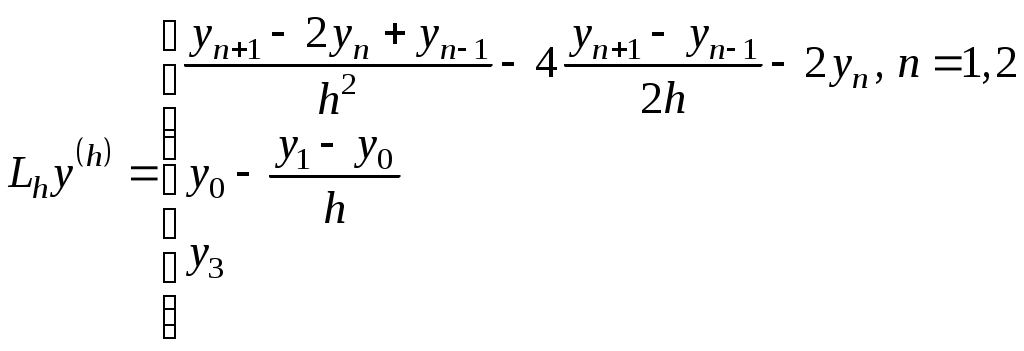 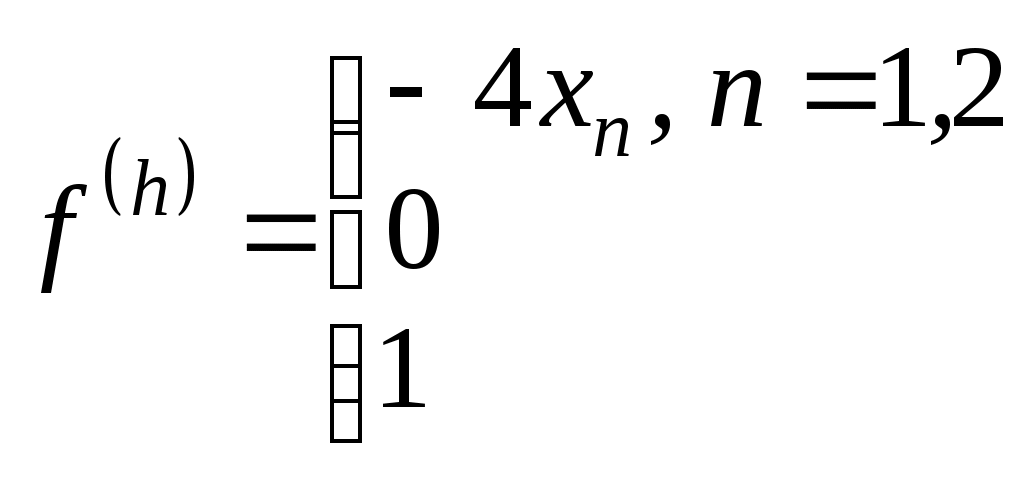 Аппроксимация дифференциального уравнения выполнена со вторым порядком точности. Аппроксимация краевого условия на левой границе  выполнена с первым порядком точности, т.к. для производной использовался шаблон с первым порядком аппроксимации. Краевое условие на правой границе  выполняется точно. Следовательно, разностная схема имеет первый порядок аппроксимации.Ответ: построена разностная схема первого порядка аппроксимации. Получена система линейных алгебраических уравнений с трехдиагональной матрицей, для решения которой применим метод прогонки. Задания для самостоятельного решения. Дана краевая задача для обыкновенного дифференциального уравнения второго порядка. Записать для нее дифференциальный оператор и правую часть задачи. Составить разностную схему, используя центральные разности второго порядка аппроксимации. Записать для нее разностный оператор и правые части. Определить порядок аппроксимации полученной разностной схемы. Получить систему уравнений с трехдиагональной матрицей. Проверить выполнение условия применимости метода прогонки. Для численного решения задачи методом конечных разностей область изменения переменной разбить на три отрезка с шагом h = 1/3 , полагая xn= x0 + nh , n =1,2,3, x0 = 0, значения искомой функции в узлах сетки обозначить y0, y1, y2, y3.1. y′′ +3 y′ - 5y= 2x, y(0) + 2y′(0) = 0 y(1) - y′(1) = 1 2. y′′ - 5 y′ - 7y= 3x, y(0) = 1 y(1) = 3 2. Метод стрельбы Теория для общего случая – см. Годунов, Рябенький, с. 166. Рассмотрим краевую задачу для обыкновенного дифференциального уравнения второго порядка (линейного):  ,   ,  Рассмотрим теперь две задачи Коши , (1) ,  и  , (2) ,  Обозначим через  решение задачи Коши (1),  - решение задачи Коши (2). В силу линейности дифференциального уравнения функция  является его решением, причем  . Из условия  выразим  (вывести формулу самостоятельно). Таким образом, решение краевой задачи с линейным дифференциальным уравнением свелось к решению двух задач Коши. В случае нелинейного дифференциального уравнения организуется итерационный процесс.Для численного решения задач Коши методом конечных разностей область изменения переменной разобьем на N отрезков с шагом h = 1/N , полагая xn= x0 + nh , n =1,2,…N, x0 = a, значения искомой функции в узлах сетки обозначим y0, y1, … yN.Составим разностную схему для уравнения в узлах сетки x2, …xN , используя центральные разности второго порядка аппроксимации. Для аппроксимации производной во втором начальном условии используем правую разность. Обозначим через  численное решение задачи Коши (1),  - численное решение задачи Коши (2). В силу линейности разностного уравнения функция  является его решением, причем  . Из условия  выразим (вывести формулу самостоятельно).Упражнение 1. Рассмотрим краевую задачу для обыкновенного дифференциального уравнения второго порядка (линейного): ,  ,  , .Вместо этой краевой задачи будем решать две задачи Коши с начальными условиями: ,  и ,  .Для численного решения задач Коши методом конечных разностей область изменения переменной разобьем на N=10 отрезков с шагом h = 1/N , полагая xn= x0 + nh , n =1,2,…N, x0 = 0, значения искомой функции в узлах сетки обозначим y0, y1, … yN.Составим разностную схему для уравнения в узлах сетки x1, xN , используя центральные разности второго порядка аппроксимации.  .Приведем подобные слагаемые:  Для второго начального условия:  или  Разностная схема первой задачи Коши: 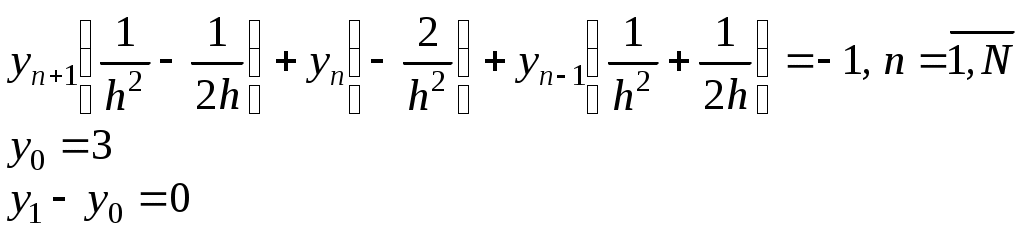 Разностная схема второй задачи Коши:  Решаем обе задачи Коши по полученным рекуррентным соотношениям.  . Точное решение краевой задачи  . В таблице приведены результаты расчетов с пятью знаками после запятой и абсолютная погрешность. На рисунке приведены графики полученных решений.
 Ответ: получено приближенное решение краевой задачи методом стрельбы. Задание для самостоятельной работы. 1. Повторить решение рассмотренной задачи в Excel. 2. Решить краевую задачу для обыкновенного дифференциального уравнения второго порядка (линейного) методом стрельбы. Для расчетов использовать Excel. Привести таблицу значений и построить графики. y′′ - 5 y′ - 7y= 3x, y(0) = 1 y(1) = 3 |