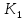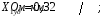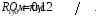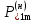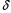1. Задание
 Скачать 0.55 Mb. Скачать 0.55 Mb.
|
1. ЗаданиеВариант №5.
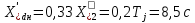
 Рис. 1 – Расчетная схема. 2. Составление схемы замещения для расчета токов короткого замыкания.Токи короткого замыкания могут быть найдены в именованных или относительных единицах. Заданную электрическую сеть можно считать сложной, поэтому решение выполним в относительных единицах. Произвольно принимаем значение базисной мощности 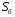 и базисного напряжения и базисного напряжения 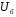 . В качестве базисного напряжения принимаем напряжение линии 110 кВ, в конце которой находиться точка к.з. . В качестве базисного напряжения принимаем напряжение линии 110 кВ, в конце которой находиться точка к.з.Uб1= 330 кВ Sб = 200 МВА. Базисное напряжение той ступени, где находится генератор равно:   Для расчетов токов короткого замыкания по заданной расчетной схеме (Рис. 1) составим схему замещения (Рис. 2). 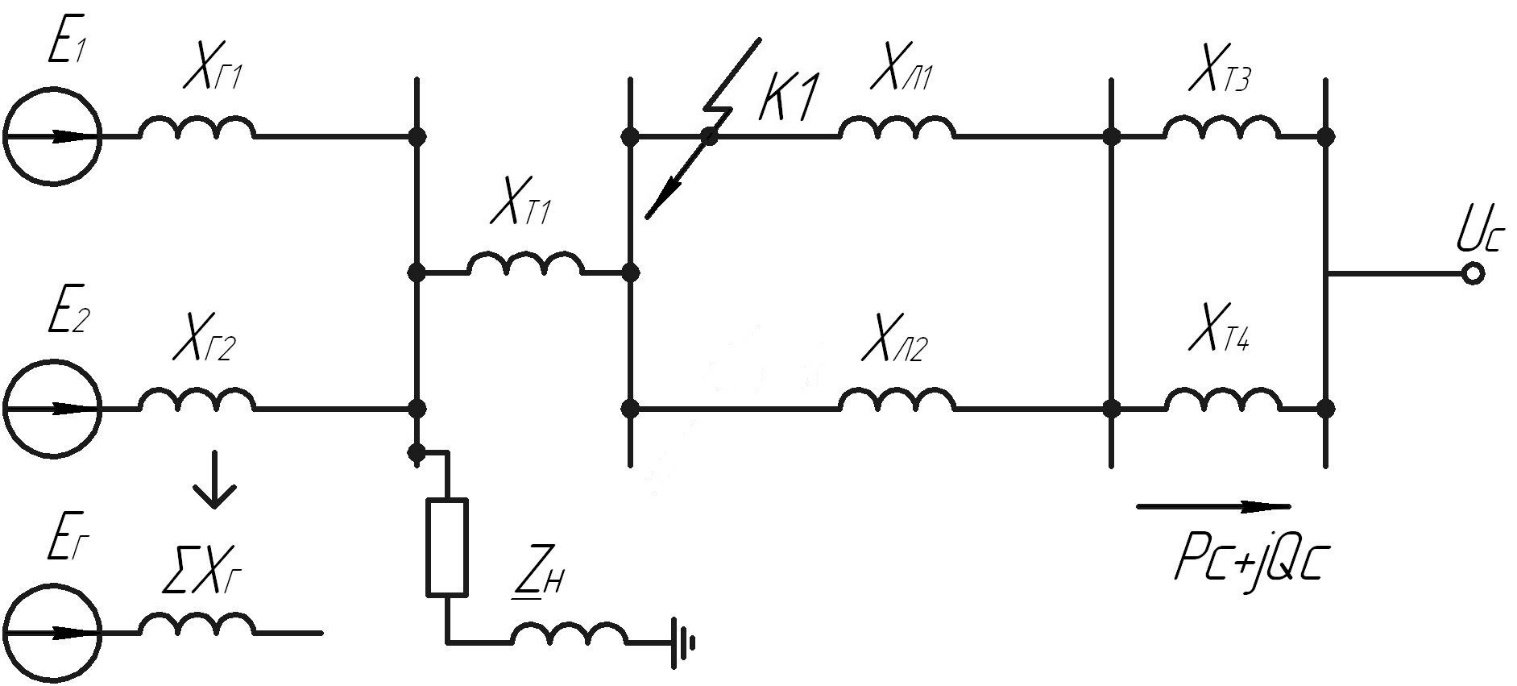 Рис. 2 – Схема замещения. Следовательно, сверхпереходное сопротивление генератора в относительных единицах при Sб = 10 МВА, будет равно 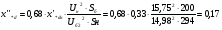 . .Переходное сопротивление генератора при выбранных базисных условиях равно  . .Сопротивление обратной последовательности: 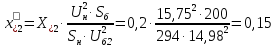 Электромеханическая постоянная генератора 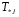 в относительных единицах равна: в относительных единицах равна: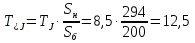 Сопротивления трансформаторов в относительных единицах равны: 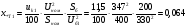 , , . .При расчете сопротивлений трансформаторов удобно принимать номинальные напряжения ступеней ближайших к базисной ступени трансформации. Индуктивное сопротивление линии электропередачи равно 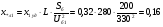 . .Напряжение и номинальная мощность на шинах электроэнергетической системы в относительных единицах 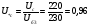 . .Мощность, передаваемая в систему: 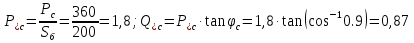 Мощность, передаваемая на нагрузку: 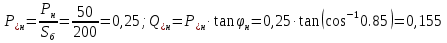 3. Определение ЭДС генератора в переходном и сверхпереходном режимах. Определим ЭДС генератора 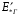 в переходном режиме. Для этого сначала определим напряжение на шинах генератора при условии, что напряжение системы остается неизменным. в переходном режиме. Для этого сначала определим напряжение на шинах генератора при условии, что напряжение системы остается неизменным.  где 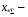 суммарное эквивалентное реактивное сопротивление электрической сети до генератора в относительных единицах. суммарное эквивалентное реактивное сопротивление электрической сети до генератора в относительных единицах.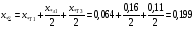    Сопротивление нагрузки: 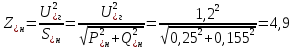  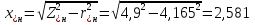 Потери реактивной мощности в сети (до генератора): 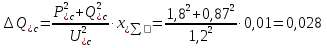 Полная мощность, отдаваемая генераторами: 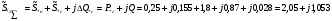 Мощность, отдаваемая каждым генератором:  Определим ЭДС генератора в переходном режиме: 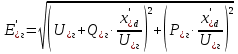 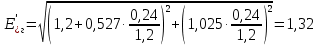   Угол между 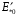 и и 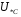 равен равен  ЭДС генератора в сверхпереходном режиме: 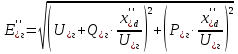 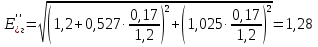  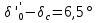 Угол между 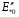 и и 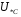 равен равен  4. Определение периодической составляющей тока трехфазного короткого замыкания.Определим токи трехфазного короткого замыкания в точке k. Объединив параллельные ветви 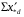 и и 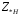 , а также , а также  и и 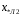 , получим схему на рисунке 3. , получим схему на рисунке 3.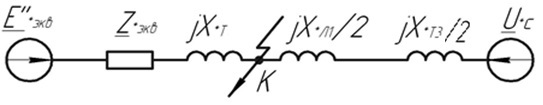 Рис. 3 – Упрощенная схема замещения 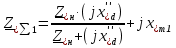 . . 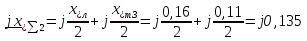 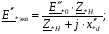 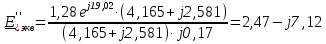 Периодическая составляющая тока трехфазного короткого замыкания в генераторной ветви: 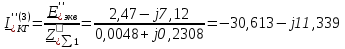 Периодическая составляющая тока трехфазного короткого замыкания в ветви от электрической системы: 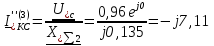 Суммарный ток трехфазного короткого замыкания в точке k: 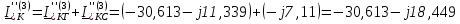 В именованных единицах: 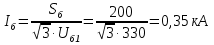 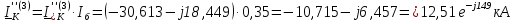 5. Составление схем замещения для токов прямой, обратной и нулевой последовательностей.При составлении схемы замещения для токов прямой последовательности воспользуемся упрощенной схемой замещения, к которой добавим источник напряжения прямой последовательности. 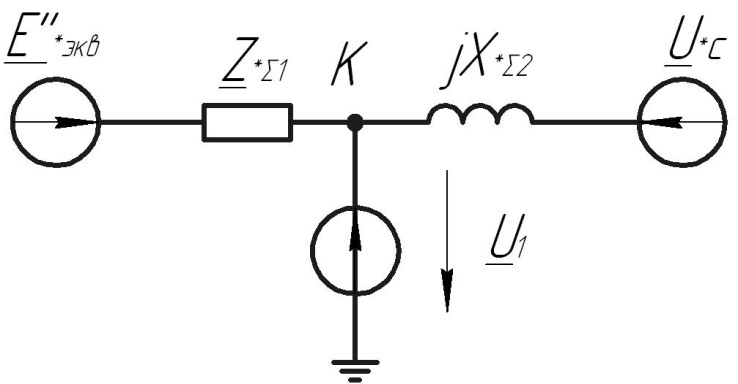 Рис. 4 – Схема замещения для токов прямой последовательности. Сворачивая схему относительно точки короткого замыкания, получим эквивалентную схему замещения для токов прямой последовательности. 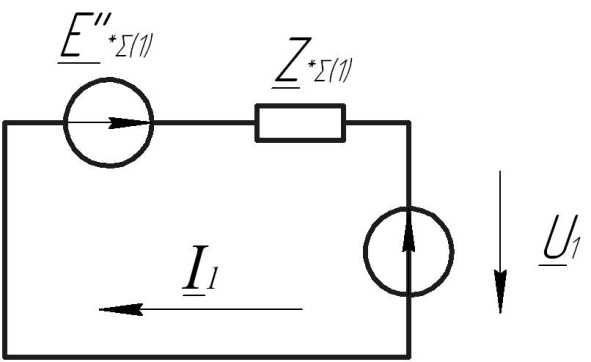 Рис. 5 – Схема замещения для токов прямой последовательности. 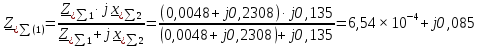   Этой схеме соответствует уравнение: 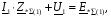 (1). (1).Для токов обратной последовательности 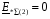 , вместо , вместо  будет будет 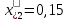 . .После преобразований, аналогичных предыдущим, получаем схему для токов обратной последовательности и уравнение: 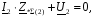 (2). (2).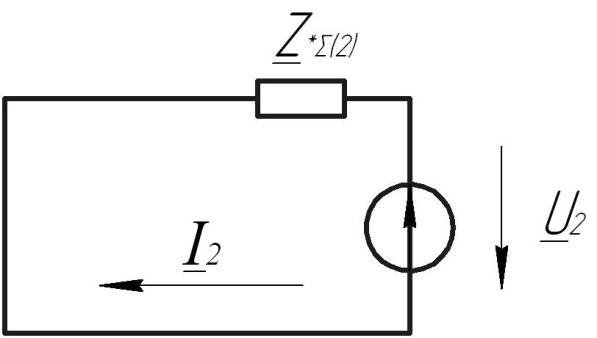 Рис. 6 – Схема замещения для токов обратной последовательности 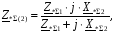 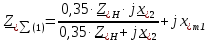 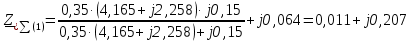 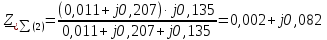 Для токов нулевой последовательности схема отличается от двух предыдущих схем. Так как нейтрали трансформаторов заземлены, то получаем схем, представленную на рис. 7. 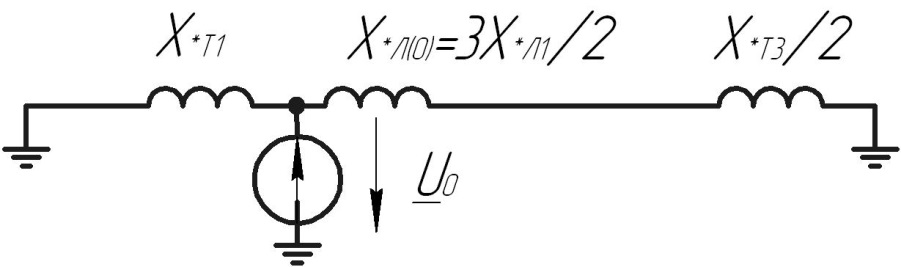 Рис. 7 – Схема замещения для токов нулевой последовательности Объединив параллельные ветви, получим окончательную схему для токов нулевой последовательности (рис. 8) и уравнение:  (3). (3).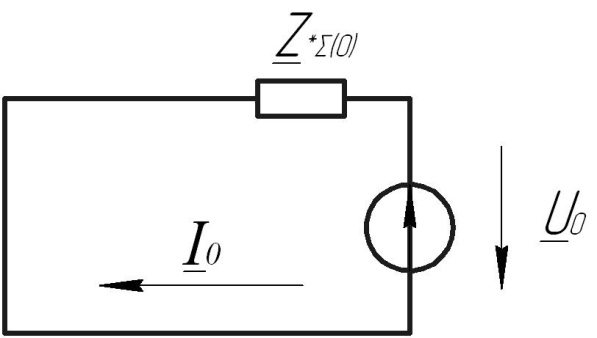 Рис. 8 – Схема замещения для токов нулевой последовательности 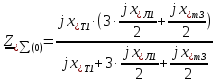 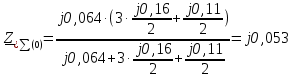 6. Расчет токов однофазного, двухфазного и двухфазного на землю коротких замыканий.Основная система уравнений имеет вид:  6.1. Расчет токов однофазного короткого замыкания.Граничными условиями при замыкании фазы А будут являться: равенство нулю токов в фазах В и С, а также напряжения в месте короткого замыкания: 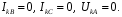 Тогда, раскладывая напряжения и токи на симметричные составляющие и используя граничные условия, решение основной системы уравнений для тока в поврежденной фазе будет иметь вид: 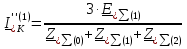  В именованных единицах:  6.2. Расчет токов двухфазного короткого замыкания.Граничными условиями при замыкании фаз В и С будут являться: равенство нулю тока в фазе А, напряжений фаз В и С вместе короткого замыкания, а также равенство нулю суммы токов в фазах В и С.  Тогда токи в поврежденных фазах будут равны:  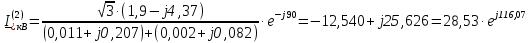  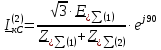 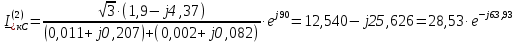 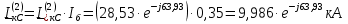 6.3. Расчет токов двухфазного короткого замыкания на землю.Граничными условиями при замыкании фаз В и С на землю будут являться: 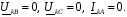 Тогда ток прямой последовательности рассчитывается как:  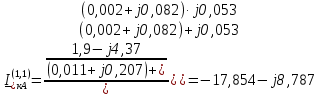 Соответственно токи в поврежденных фазах равны: 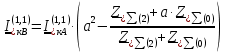 где  фазовый множитель. фазовый множитель. 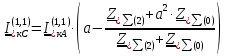 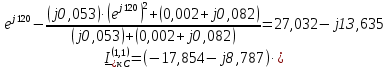  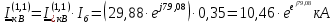 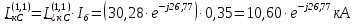 7. Расчет динамической устойчивости электрической системы при аварийном режиме.7.1 Расчет угловых характеристик активной мощности генератора.Расчет угловых характеристик мощности ведется при условии, что генератор снабжен системой АРВ ( 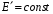 ). В этом случае зависимость активной мощности от относительного положения ротора синхронного генератора имеет следующий вид: ). В этом случае зависимость активной мощности от относительного положения ротора синхронного генератора имеет следующий вид: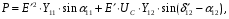 где  – переходная ЭДС генератора; – переходная ЭДС генератора;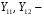 - входная и взаимная проводимости цепи. - входная и взаимная проводимости цепи.Для расчета этих проводимостей используется метод преобразования схемы, при котором исходная схема преобразуется к виду, показанному на рисунке 9. 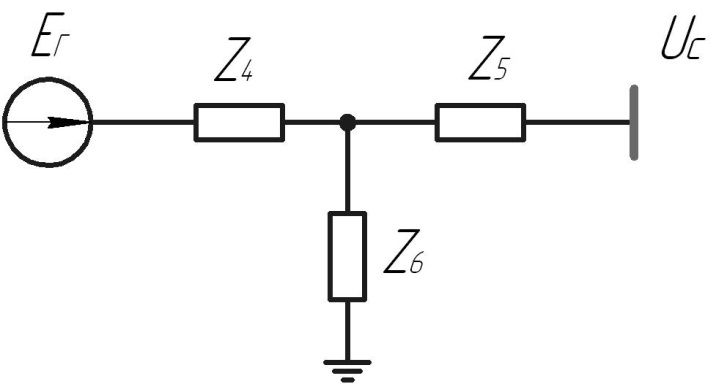 Рис. 9 – Преобразованная схема замещения. Для этой схемы:  1. Нормальный режим. 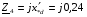 , ,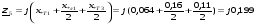 , ,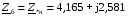 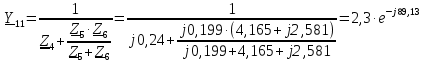 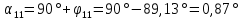 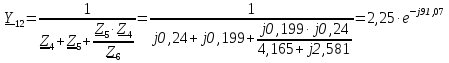 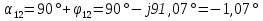 2. Аварийный режим. Аварийным режимом будем считать двухфазное КЗ на землю. При расчете проводимостей введем в исходную схему замещения «аварийный шунт» 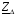 . .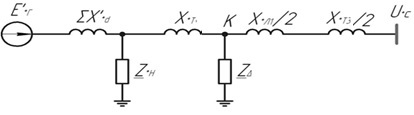 Рис. 10 – Схема для расчета аварийного режима. Сопротивление «аварийного шунта» при двухфазном КЗ на землю равно: 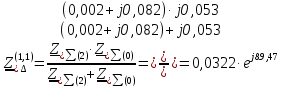 Для того чтобы получить схему на рисунке 9, необходимо преобразовать треугольник сопротивлений 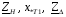 в эквивалентную звезду. в эквивалентную звезду. 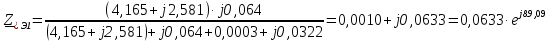 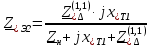 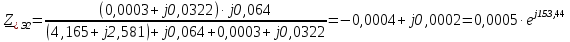  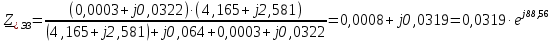 Тогда для этого случая: 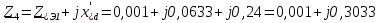 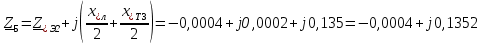 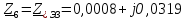 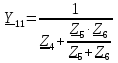 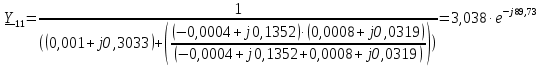    3. Послеаварийный режим. Если линия двухцепная, то послеаварийным режимом будем считать отключение поврежденной цепи. В этом случае расчет производится также как для нормального режима, но учитывают только одну воздушную линию. Тогда получим: 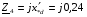 , , , ,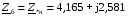 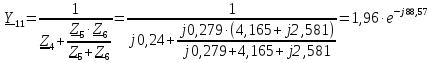  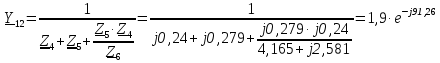 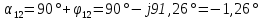 Определим электромагнитную мощность, отдаваемую генератором, для каждого режима. 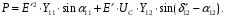
 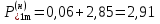
 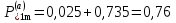
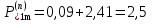 Построим зависимости  для нормального, аварийного и послеаварийного режимов. для нормального, аварийного и послеаварийного режимов. Таблица 1 – Данные для построения зависимостей 
Рисунок 11 – Угловые характеристики мощности для нормального (н), аварийного (а) и послеаварийного (п) режимов Прямая 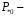 мощность турбины. До короткого замыкания режим работы соответствовал точке 1. В момент короткого замыкания рабочая точка перемещается вниз (точка 2), где мощность турбины. До короткого замыкания режим работы соответствовал точке 1. В момент короткого замыкания рабочая точка перемещается вниз (точка 2), где 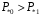 , и начинается ускорение ротора генератора, угол , и начинается ускорение ротора генератора, угол 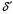 увеличивается. Если он станет больше критического увеличивается. Если он станет больше критического  , то генератор выйдет из синхронизма. Определим этот угол (точка 5). , то генератор выйдет из синхронизма. Определим этот угол (точка 5). 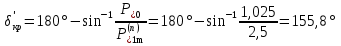 где 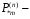 амплитуда активной мощности в послеаварийном режиме. амплитуда активной мощности в послеаварийном режиме.Для того чтобы угол 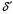 не достиг критического значения, аварийный режим должен быть отключен значительно раньше, так как и после его отключения увеличение угла прекращается не сразу из-за инерции процесса. Предельный угол отключения можно определить из выражения: не достиг критического значения, аварийный режим должен быть отключен значительно раньше, так как и после его отключения увеличение угла прекращается не сразу из-за инерции процесса. Предельный угол отключения можно определить из выражения: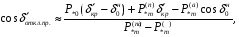  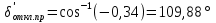 7.2 Расчет предельного времени отключения короткого замыкания. Предельное время отключения определяется путем решения дифференциального уравнения движения ротора генератора, применяя метод последовательных интервалов. При расчете выбираем интервал времени Δt=0,05 с. Активная мощность аварийного режима в начальный момент времени:  Если выразить время и электромеханическую постоянную генератора в секундах, а угол – в градусах, то приращение угла в первый интервал будет равно: 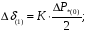    Угол к концу первого интервала: 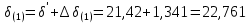 Приращение угла во втором и последующие интервалы рассчитывается как:  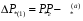 (при угле (при угле 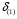 ) и так далее. ) и так далее.Результаты расчетов занесены в таблицу 1. Таблица 2 – Данные расчета уравнения движения ротора
По результатам расчетов строим график (рис. 12) По графику определяем предельное время отключения, tпр= с Рисунок 12 – График зависимости угла движения ротора от времени |

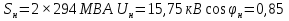

 :
: 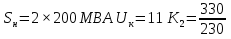
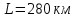

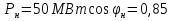
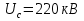 .
.