математика вопрос 10. 10. Понятие формулы алгебры высказываний. Логическое значение составного высказывания. Составление таблиц истинности для формул
 Скачать 93.54 Kb.
|
|
10. Понятие формулы алгебры высказываний. Логическое значение составного высказывания. Составление таблиц истинности для формул. Формула алгебры высказываний – это выражение, составленное из переменных высказываний с помощью логических операций, и обращающееся в конкретное высказывание при подстановке вместо переменных высказываний, конкретных высказываний. Формула, составленная в алфавите логики высказываний,удовлетворяет следующим требованиям: Любая высказывательная переменная является формулой. Если  и  –формулы,то,  – тоже формулы.Только те выражения являются формулами, для которых выполняются пункты 1 и 2. ПРИМЕР ФОРМУЛ   Логическое значение составного высказывания  Если в формулу алгебры высказываний  вместо пропозициональных переменных  подставитьконкретные высказываниясоответственно, то получится некоторое новое составное высказывание  . Оно называется конкретизацией формулы на выборе высказываний .ТЕОРЕМА. Логическое значение составноговысказывания равно значениюформулы на наборе  логических значений составляющих высказываний , т.е. Составление таблиц истинности для формул Правило.На основании теоремы можно для данной формулы  алгебры высказываний найти логические значения всех тех высказываний, в которые формула превращается при подстановке вместо всех ее пропозициональных переменных различных конкретных высказываний. При этом говорят о логическом значении самой формулы и о логических значениях ее пропозициональных переменных. При нахождении логических значений формулы, соответствующих всевозможным наборам значений ее пропозициональных переменных, удобной формой записи является табличная форма. Пример. Составим таблицу истинности для формулы 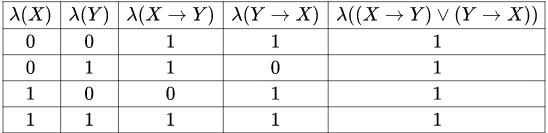 . В первых двух столбцах таблицы выпишем всевозможные пары логических значений, которые могут принимать пропозициональные переменные  и  (точнее, те высказывания, которые могут быть подставлены в формулу вместо пропозициональных переменных и ). В последующих столбцах выписываем логические значения формул  и , образующих так называемую порождающую последовательность для данной формулы. Руководствуемся при этом определениями логических операций импликации и дизъюнкции. В результате получаем таблицу: Первые два столбца и последний столбец составленной таблицы задают соответствия между логическими значениями исходных высказываний и логическим значением составного высказывания, получаемого по данной формуле. Эти три столбца и образуют таблицу истинности данной формулы. Остальные два столбца (для логических значений  и  носят вспомогательный, промежуточный характер. |