Топтыгин. топтыгин. 156. Проводящий шар радиуса R1 находится в однородном диэлектрике с проницаемостью 1
 Скачать 169.09 Kb. Скачать 169.09 Kb.
|
|
156. Проводящий шар радиуса R1 находится в однородном диэлектрике с проницаемостью ε1. Внутри шара имеется сферическая полость радиуса R2 заполненная однородным диэлектриком с проницаемостью ε2. В полости на расстоянии а от ее центра (a < R2) расположен точечный заряд q. Найти поле φ во всем пространстве.  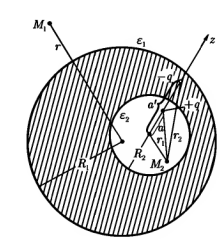 Вне шара потенциал поля совпадает с полем заряда q, помещенного в центр шара: 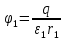 Внутри шара в материале проводника: 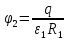 Найдем потенциал в полости шара: 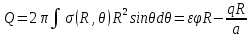 отсюда 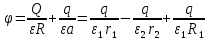  отсюда  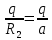 – из равенства потенциалов => – из равенства потенциалов => 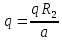 217. Поверхность проводника образована двумя сферами с радиусами R1 и R2, пересекающимися по окружности радиуса a. Найти емкость С этого проводника, исходя из результата решения задачи 206 о проводящем клине в поле точечного заряда и применяя метод инверсии. УКАЗАНИЕ. Поверхность рассматриваемого проводника описывается в тороидальных координатах уравнениями ξ = ξ1 = const ξ = ξ2= const (sin ξ1 = ± a/R1 , sin ξ2 = ± a/R2) Найдем угол пересечения сферических поверхностей  (отсчет ведем вне проводника): (отсчет ведем вне проводника): Из указаний, будем использовать метод инверсии. Для этого выберем центр инверсии O на линии пересечения сфер. Зададим радиус инверсии равным 2а. 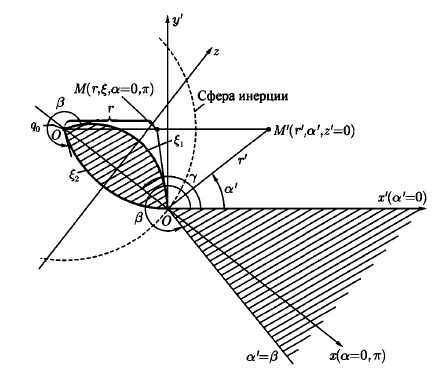 В результате получаем клин с двугранным углом В результате получаем клин с двугранным углом  и ребром из оси z’, перпендикулярным плоскости симметрии (α = 0,π). и ребром из оси z’, перпендикулярным плоскости симметрии (α = 0,π).В результате инверсии, в точке О появился заряд 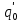 равный равный 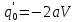 Согласно рисунку 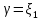 при условии отсчета при условии отсчета  от грани клина, в которую переходит сферическая поверхность от грани клина, в которую переходит сферическая поверхность 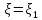 . В результате инверсии поверхности ξ = ξ1 = constпереходят в плоскости α’ = const: . В результате инверсии поверхности ξ = ξ1 = constпереходят в плоскости α’ = const: Выразим расстояния r и r’ через координаты ρ, ξ точки наблюдения М. Координата ρсвязана с декартовыми: 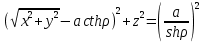 ξ связана с декартовыми координатами следующим образом: 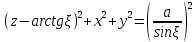 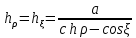  Из данных выражение и подобия треугольников ОО’M’ и OO’M получаем:   Потенциал поля точечного заряда в клиновидной области можно найти по формуле:  Потенциал V пропорционален находящемуся на проводнике заряду q:  Откуда следует:  Выразим q из  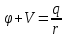  При r →∞ получаем:  Используя соотношение для  и ξ, получим: и ξ, получим: После вычисления получим:  или 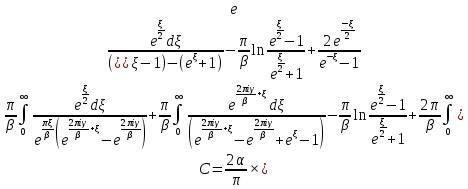 320. Пусть в плазме, описанной в предыдущей задаче, существует постоянное электрическое поле E. Получить в линейном по H0 приближении связь между плотностью тока j и электрическим полем Е. Найти тензор электропроводности. УКАЗАНИЕ. Уравнение движения электрона решать методом последовательных приближений. Из условия задачи известно, что рассматривается плазма, описываемая уравнением движения электронов в постоянном электрическом поле: 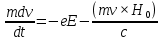 где m - масса электрона,  – скорость электрона, e – заряд электрона, E – электрическое поле, – скорость электрона, e – заряд электрона, E – электрическое поле,  – магнитное поле, c – скорость света. – магнитное поле, c – скорость света.Для решения задачи необходимо получить связь между плотностью тока j и электрическим полем Е в линейном по  приближении, а также найти тензор электропроводности. приближении, а также найти тензор электропроводности.Решение задачи начинается с выражения плотности тока через скорость электронов: j = -eNv где N - концентрация электронов. Следующим шагом в решении является выражение скорости электронов через электрическое поле и магнитное поле, используя метод последовательных приближений:  где 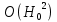 - означает члены, содержащие квадраты магнитного поля и выше, которые пренебрегаются при линейном приближении. - означает члены, содержащие квадраты магнитного поля и выше, которые пренебрегаются при линейном приближении.Подставляя это выражение для скорости в формулу для плотности тока, получаем:  Или 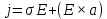 где 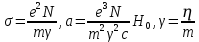 В этом выражении первое слагаемое соответствует дрейфовому току, вызванному электрическим полем, а второе слагаемое - току Холла, вызванному магнитным полем. Далее, с помощью линейной алгебры можно выразить электрическое поле через плотность тока, учитывая также вклад тока Холла. Результатом является следующее выражение: 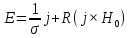 R - постоянная Холла, определяемая как: 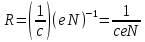 Представим Е как  где  - тензор сопротивления; 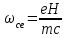 - электронная циклотронная частота; - электронная циклотронная частота;  - подвижность. - подвижность. Поскольку  то для получения компонентов тензора проводимости необходимо найти матрицу, обратную (4). В результате получаем:  И наконец, тензор электропроводности определяется как: 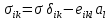 где σ - электропроводность без учета магнитного поля,  - символ Кронекера (равен 1 при i = k и 0 при i ≠ k), - символ Кронекера (равен 1 при i = k и 0 при i ≠ k),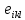 - символ Леви-Чивиты (равен 1 при циклической перестановке индексов i, k, l и -1 при обратной перестановке), - символ Леви-Чивиты (равен 1 при циклической перестановке индексов i, k, l и -1 при обратной перестановке), 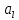 - компоненты тензора магнитной восприимчивости в линейном приближении по - компоненты тензора магнитной восприимчивости в линейном приближении по  . .Тензор электропроводности связывает плотность тока и электрическое поле в плазме. Он имеет диагональные компоненты, которые соответствуют направлениям осей координат, и недиагональные компоненты, которые характеризуют взаимодействие между различными направлениями. Тензор электропроводности может быть использован для описания электропроводности в различных условиях и материалах, в том числе в плазме. 400. Рассмотреть в предыдущей задаче зависимость поляризации от сдвига фаз χ для случая a = b. 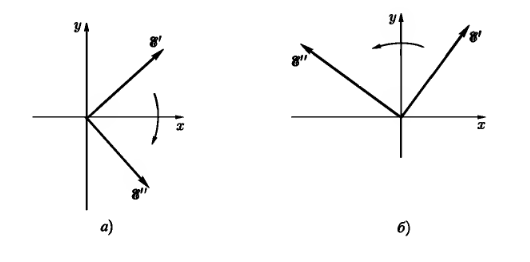 Рассмотрим поляризацию при разных значениях  : :а)  . Поляризация линейная и плоскость поляризации проходит через биссектрису угла между осями . Поляризация линейная и плоскость поляризации проходит через биссектрису угла между осями 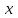 и и 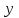 (рисунок а). (рисунок а).б) 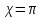 . Поляризация тоже линейная и плоскость поляризации проходит через биссектрису угла между осями . Поляризация тоже линейная и плоскость поляризации проходит через биссектрису угла между осями 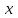 и и  (рисунок б). (рисунок б).в) 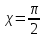 . Поляризация круговая правая, (рисунок а). . Поляризация круговая правая, (рисунок а).г)  . Поляризация круговая левая, (рисунок б). . Поляризация круговая левая, (рисунок б).д) 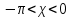 . Поляризация эллиптическая правая, . Поляризация эллиптическая правая, 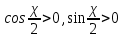 , (рисунок а). , (рисунок а).е)  . Поляризация эллиптическая левая, (рисунок б). . Поляризация эллиптическая левая, (рисунок б).434. Решить предыдущую задачу для случая, когда оптическая ось кристалла параллельна его поверхности и составляет угол α с плоскостью падения. Обыкновенный луч подчиняется закону преломления, поэтому  где  - угол между обыкновенным лучом и нормалью к поверхности - угол между обыкновенным лучом и нормалью к поверхности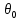 – угол падения – угол падения – диэлектрическая проницаемость – диэлектрическая проницаемость – магнитная проницаемость среды – магнитная проницаемость средыИз (1) следует: 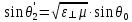 Cледовательно, обыкновенный луч лежит в плоскости падения и составляет с нормалью к поверхности угол  . .Рассмотрим необыкновенную волну. Волновой вектор 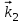 необыкновенной волны также лежит в плоскости падения и составляет с нормалью угол необыкновенной волны также лежит в плоскости падения и составляет с нормалью угол 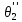 : : Cледовательно, необыкновенный луч не лежит в плоскости падения. Необыкновенный луч расположен в плоскости с волновым вектором 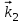 оптической осью, с которой составляет угол оптической осью, с которой составляет угол  : : 463. Найти дифференциальное и полное сечения рассеяния плоской волны длиной 𝛌 на идеально проводящем цилиндре высотой 2h и радиуса a <<, h << 𝛌. Исследовать различные случаи поляризации падающей волны. Цилиндр аппроксимировать вытянутым эллипсоидом вращения с полуосями a и h. С  делаем рисунок. Выберем систему координат. Вектор kпервичной волны лежит в плоскостиxz. По условию необходимо цилиндр аппроксимировать вытянутым эллипсоидом вращения с полуосями a и h. делаем рисунок. Выберем систему координат. Вектор kпервичной волны лежит в плоскостиxz. По условию необходимо цилиндр аппроксимировать вытянутым эллипсоидом вращения с полуосями a и h. . Продольная и поперечная поляризуемость эллипсоида в . Продольная и поперечная поляризуемость эллипсоида в  больше его электрической и магнитной поляризуемостей. Следовательно, сечение рассеяния будет сильно зависеть от того, имеется ли продольная составляющая электрического поля в падающей волне. И, если данная составляющая достаточно велика, то вторичное излучение обусловлено больше его электрической и магнитной поляризуемостей. Следовательно, сечение рассеяния будет сильно зависеть от того, имеется ли продольная составляющая электрического поля в падающей волне. И, если данная составляющая достаточно велика, то вторичное излучение обусловлено  - компонентой электрического дипольного момента. Пренебрегая остальными компонентами электрического момента и магнитным моментом и выбирая - компонентой электрического дипольного момента. Пренебрегая остальными компонентами электрического момента и магнитным моментом и выбирая  в плоскости в плоскости  , получаем: , получаем: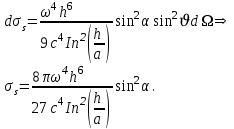 В случае, если  , то рассеяние обусловлено поперечной компонентой электрического момента и магнитным моментом, которые имеют одинаковый порядок величин. Тогда, , то рассеяние обусловлено поперечной компонентой электрического момента и магнитным моментом, которые имеют одинаковый порядок величин. Тогда,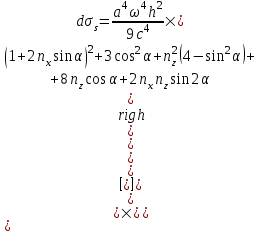 где 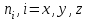 - компоненты единичного вектора, указывающие направление рассеяние. - компоненты единичного вектора, указывающие направление рассеяние. Для неполяризованной волны сечение рассеяния будет 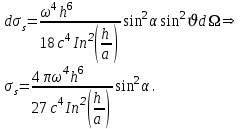 |
