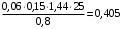2 Расчет балочного сборного перекрытия 2
 Скачать 0.57 Mb. Скачать 0.57 Mb.
|
 Содержание2 Расчет балочного сборного перекрытия 2 2.1 Компоновка конструктивной схемы балочного сборного перекрытия 2 2.2 Расчет полки ребристой плиты перекрытия 3 2.3 Расчет поперечных ребер плиты 5 2.4 Расчет продольного ребра 8 2.6 Потери предварительного напряжения арматуры 14 2.7 Проверка образования трещин 16 2.8 Расчет по раскрытию трещин. 17 2.9 Расчет прогиба плиты 21 2 Расчет балочного сборного перекрытия2.1 Компоновка конструктивной схемы балочного сборного перекрытия Рисунок 7– Конструктивная схема балочного сборного перекрытия Неразрезные ригели располагаются в продольном направлении здания. Ребристые плиты располагаются в поперечном направлении. По результатам компоновки приняты плиты номинальной шириной 1600 мм. В крайних пролетах монолитные участки шириной 800 мм. Геометрические размеры плиты 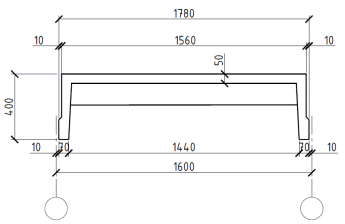 Рисунок 8 – Поперечное сечение плиты 2.2 Расчет полки ребристой плиты перекрытияВысота поперечного сечения ригеля 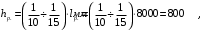 Ширина поперечного сечения ригеля 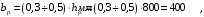 Высота сечения плиты 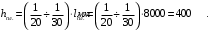 Задаемся шагом поперечных ребер, при условии 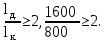 Назначаем шаг поперечных ребер плиты равный 800мм. Для расчета полки плиты перекрытия выделяем полосу шириной 1 м. Полка будет работать как неразрезная балка, опорами которой служат поперечные ребра жесткости. Нагрузка на 1 м полки будет равна нагрузке на 1 м2 перекрытия. Таблица 7 – Нагрузки на 1 м2 полки ребристой плиты
Коэффициент надежности по назначению для II класса ответственности зданий и сооружений γn = 0,95. С учетом коэффициента надежности по классу ответственности здания: 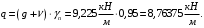 По СНиП 2.03.01-84* «Бетонные и железобетонные конструкции» определяем прочностные и деформативные характеристики бетона и арматуры заданного класса с учетом влажности окружающей среды. Бетон тяжелый, тепловая обработка, класса В20 γb2 = 0,9 ; Rb = 11,5∙0,9 МПа= 10,35МПа; Еb = 27000 МПа; h0 = h – a = 50-12=38мм. Принимаю для сетки арматуру Вр-I ⌀4 мм с Rs=365 МПа. Выполняем подбор сечения арматуры сеток Определяю величину изгибающих моментов в пролетах и на опорах полки: в первом пролёте и на первой промежуточной опоре 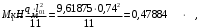 где q – расчетная распределенная нагрузка; l01 – расчетный пролет крайней плиты в коротком направлении. в средних пролетах и на средних опорах 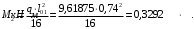 Подбор арматурной сетки по наибольшему моменту ( 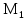 ) )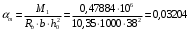 по приложению 4/2/нахожу η=0,984. 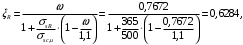 где 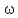 – характеристика сжатой зоны бетона, определяемая по формуле – характеристика сжатой зоны бетона, определяемая по формуле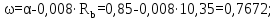 α − коэффициент, принимаемый для тяжелого бетона 0,85; σsR − напряжение в арматуре, принимаемое для класса A-III равным расчетному сопротивлению арматуры; σsс,u − предельное напряжение в арматуре сжатой зоны, принимаемое для 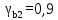 равным 500 МПа. равным 500 МПа.по /2/ определяем ξ=0,0325<ξR=0,6284; 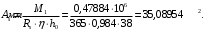 Принимаю 6 стержней ⌀3 мм Вр-I с шагом s=200мм, As = 42,4мм2. 2.3 Расчет поперечных ребер плиты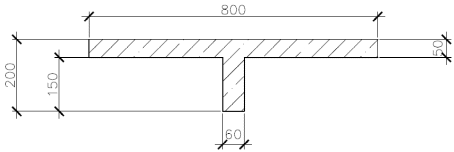 Рисунок 9 – Поперечное сечение поперечного ребра Таблица 8– Нагрузки на 1 м поперечного ребра ребристой плиты
Коэффициент надежности по назначению для II класса ответственности зданий и сооружений γn = 0,95. С учетом коэффициента надежности по классу ответственности здания: 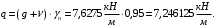 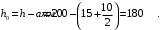 Расчетный пролет поперечного ребра принимаю равным расстоянию между осями продольных ребер, тогда расчетная схема будет иметь вид: 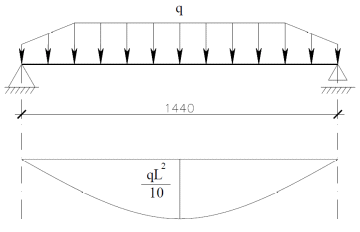 Рисунок 10 – Расчетная схема поперечного ребра Определяем изгибающий момент 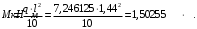 Определяем поперечную силу 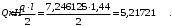 Определяем положение нейтральной оси 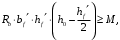 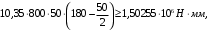 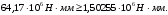 Условие выполняется, граница сжатой зоны проходит в полке, то расчет производится как для прямоугольного сечения шириной b = bf = 800 мм. Определяем коэффициент статического момента αm 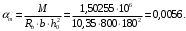 по приложению 4/2/нахожу η=0,995. Класс арматуры А-III, Rs=355МПа для Ø 6-8 мм. 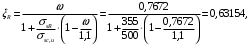 где 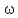 – характеристика сжатой зоны бетона, определяемая по формуле – характеристика сжатой зоны бетона, определяемая по формуле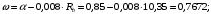 α − коэффициент, принимаемый для тяжелого бетона 0,85; σsR − напряжение в арматуре, принимаемое для класса A-III равным расчетному сопротивлению арматуры; σsс,u − предельное напряжение в арматуре сжатой зоны, принимаемое для 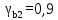 равным 500 МПа. равным 500 МПа.по /2/ определяем ξ=0,00561<ξR=0,63154; 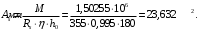 Из сортамента стержневой и проволочной арматуры принимаю 1 стержень Ø 6 мм, арматура А-III, с площадью рабочей арматуры As=28,3 мм2. Расчет поперечного ребра плиты на действие поперечной силы По /2/ из условия свариваемости принимаем поперечные стержни диаметром 3 мм класса Вр-I с числом каркасов – 1с шагом поперечных стержней s=100мм согласно требованиям /1/ п. 5.27. Аsw = 7,1 мм2; Rsw = 270 МПа; Rbt = 0,9∙0,9=0,81 МПа; Еs = 170000МПа; Еb = 27000МПа. Проверяем условие 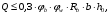 где φw1 – коэффициент учитывающий влияние хомутов, нормальных к продольной оси элемента; 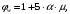 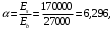 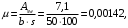 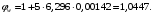 Коэффициент φb1 вычисляется по формуле 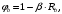 Коэффициент β = 0,01, для тяжелого бетона 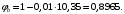 Тогда 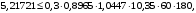 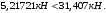 Условие выполняется. Прочность по наклонной полосе между трещинами обеспечена. Проверяем условие 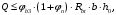 где 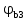 – коэффициент для тяжелого бетона принимаю равным 0,6 по /1/ п 3.3; – коэффициент для тяжелого бетона принимаю равным 0,6 по /1/ п 3.3;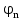 – коэффициент, учитывающий влияние продольных сил равен 0. – коэффициент, учитывающий влияние продольных сил равен 0.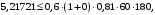 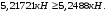 Условие выполняется, следовательно, поперечное армирование не требуется. 2.4 Расчет продольного ребра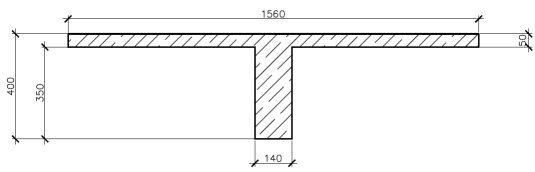 Рисунок 11 – Поперечное сечение продольного ребра Таблица 9 – Нагрузки на 1 м ребристой плиты
С учетом коэффициента надежности по классу ответственности здания: 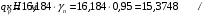 ; ;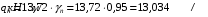 ; ;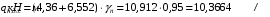 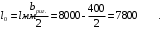 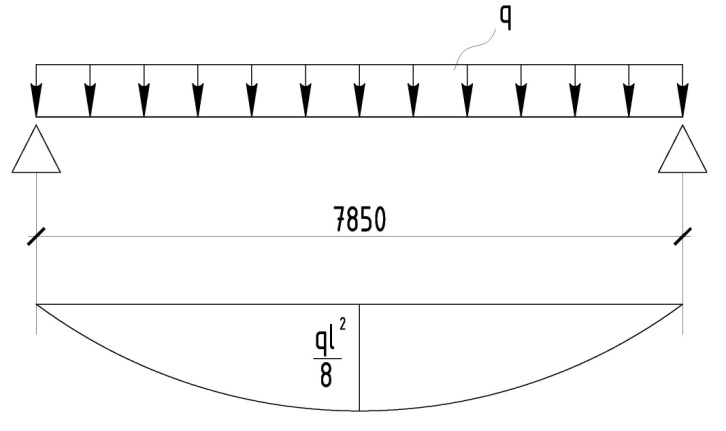 Рисунок 12 – Расчетная схема продольного ребра h0=400-30=370мм. Класс предварительно напрягаемой арматуры А-IV Rs=510 МПа Rs ser=590 МПа Расчетные усилия: Для расчетов по I группе предельных состояний: 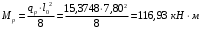 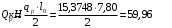 Для расчетов по II группе предельных состояний: 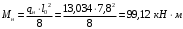 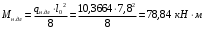 Назначаем эффективную максимальную величину предварительного напряжения арматуры: 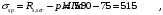 где p – (при электротермическом способе натяжения арматуры) определяется по формуле 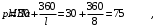 Проверяю условие (1) п. 1,23 /1/ 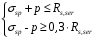 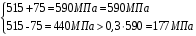 Определяем положение нейтральной оси 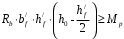 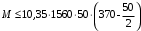 116,93·106 Н·мм < 278,52·106 Н·мм Так как условие выполняется, то граница сжатой зоны проходит в полке, и расчет производим как для прямоугольного сечения шириной 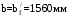 . .Определяем коэффициент статического момента αm 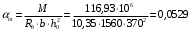 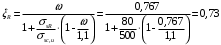 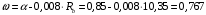 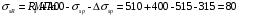 Проверяем условие ξ=0,0544<ξR=0,73; ζ=0,9728.Условие выполняется. 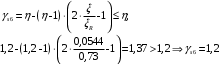 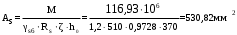 Принимаем арматуру - 2 стержня Ø20 А-IV, Аs= 628 мм2 Расчет прочности сечений, наклонных к продольной оси. Из условия свариваемости принимаем поперечные стержни диаметром 5 мм класса Вр-I с числом каркасов – 2 с шагом поперечных стержней s=150 мм согласно требованиям /1/ п. 5.27. Аsw = 19,6∙2=39,2 мм2 Rsw = 260 МПа Rbt = 0,9∙0,9=0,81 МПа Еs=170000 МПа Еb=27000 МПа Проверяем условие 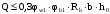 где φw1 – коэффициент учитывающий влияние хомутов, нормальных к продольной оси элемента 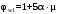 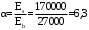 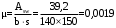 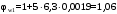 Коэффициент φb1 вычисляется по формуле 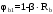 Коэффициент β = 0,01, для тяжелого бетона 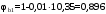 тогда: 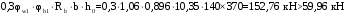 Условие выполняется, прочность по наклонной полосе между трещинами обеспечена. Проверяем условие: 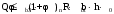 ; ;где, коэффициент φb3 согласно пункту 3.31 /1/ для тяжелого бетона принимаем равным 0,6. Коэффициент φn, учитывающий влияние продольных сил равен 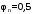 Коэффициент φb3 по /1/ п 3.31 для тяжелого бетона принимаем равным 0,6. тогда: 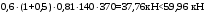 Условие не выполняется необходимо поперечное армирование. Определяю длину проекции наиболее опасного наклонного сечения на продольную ось элемента: 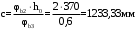 Коэффициент φb2, учитывающий влияние вида бетона, принимаем для тяжелого бетона равным 2,0. Коэффициент, φf, учитывающий влияние сжатых полок в тавровых и двутавровых элементах равен: 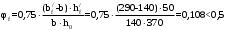 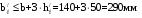 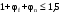 Поперечное усилие, воспринимаемое бетоном: 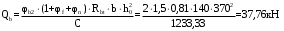 Усилие в хомутах на единицу длины элемента равняется: 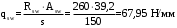 . .Определяем длину проекции наиболее опасной наклонной трещины на продольную ось элемента: 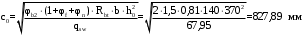 ; ;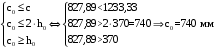 Проверяем условие: 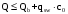 ; ;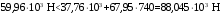 . .Условие выполняется, следовательно, прочность наклонного сечения обеспечена. 2.5 Расчет ребристой плиты по предельным состояниям II группы Согласно табл. 2 /1/ ребристая плита, эксплуатируемая в закрытом помещении и армированная напрягаемой арматурой класса A-IV должна удовлетворять 3-й категории требований по трещиностойкости, т.е. допускается непродолжительное раскрытие трещин шириной 0,4 мм и продолжительное – 0,3 мм. Прогиб плиты от действия постоянных и длительных нагрузок не должен превышать предельного значения – 2,5 см по табл.4 /1/. Определение геометрических характеристик приведенного сечения плиты 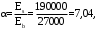 площадь приведенного сечения определяется по формуле 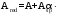 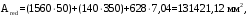 статический момент площади приведенного сечения относительно нижней грани определяется по формуле 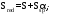 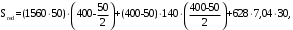 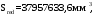 расстояние от нижней грани до центра тяжести приведенного сечения определяется по формуле 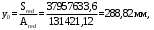 момент инерции приведенного сечения определяется по формуле 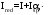 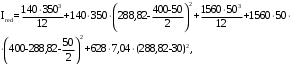 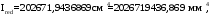 момент сопротивления приведенного сечения по нижней зоне определяется по формуле 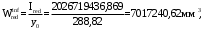 момент сопротивления приведенного сечения по верхней зоне определяется по формуле 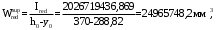 упругопластичный момент сопротивления по растянутой зоне определяется по формуле 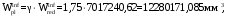 где γ = 1,75 – для таврового сечения с полкой в сжатой зоне упруго пластичный момент сопротивления по растянутой зоне в стадии изготовления и обжатия элемента определяется по формуле 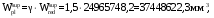 где γ = 1,5 – для таврового сечения с полкой в растянутой зоне при 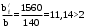 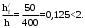 2.6 Потери предварительного напряжения арматурыОпределяем первые потери предварительного напряжения арматуры по позициям 1-6 таблицы 5 /1/. Арматура стержневая A-IV, способ натяжения электротермический. потери от релаксации напряжений в арматуре: 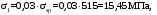 потери от температурного перепада: 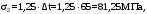 потери от деформации анкеров: 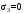 потери от трения арматуры: 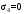 потери от деформации стальной формы: σ5=0 Таким образом, усилие обжатия PI с учетом потерь 1-5 равно: 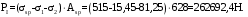 Точка приложения усилия PI совпадает с центром тяжести сечения напрягаемой арматуры, поэтому еор = у0 – а = 288,82–30 = 258,82 мм. Для определения потерь от быстронатекающей ползучести бетона вычисляем напряжение в бетоне в середине пролета от действия силы PI и изгибающего момента Mw от собственной массы плиты: 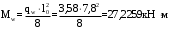 напряжение на уровне растянутой арматуры (т. е. при у = е0 = 288,82 мм) 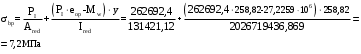 напряжение на уровне крайнего сжатого волокна (т. е. при у = h – y0 =400-288,82 = 111,18 мм) 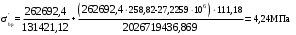 Назначаем передаточную прочность бетона Rbp = 15 МПа (Rpb,ser = 15МПа, Rpbt,ser = 1,4 МПа). потери от быстронатекающей ползучести бетона на уровне растянутой арматуры 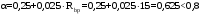 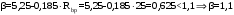 т.к 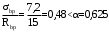 ,то ,то 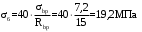 на уровне крайнего сжатого волокна 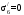 Первые потери составляют: 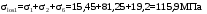 Усилие обжатия равно: 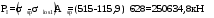 Максимальное сжимающее напряжение в бетоне от действия силы PI без учета собственной массы, принимая у = у0 = 288,82 мм 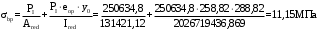 Поскольку 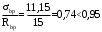 , требование п. 1.29 /1/ удовлетворяется, определяем вторые потери предварительного напряжения арматуры: , требование п. 1.29 /1/ удовлетворяется, определяем вторые потери предварительного напряжения арматуры:потери от усадки бетона 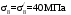 потери от ползучести бетона вычисляем напряжения в бетоне от усилия PI на уровне растянутой арматуры 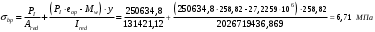 на уровне крайнего сжатого волокна 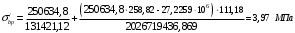 т. к. 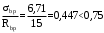 , то , то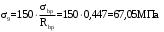 на уровне крайнего сжатого волокна: 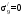 Вторые потери составляют 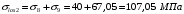 Суммарные потери составляют 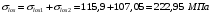 Усилие обжатия с учетом суммарных потерь составит 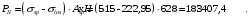 2.7 Проверка образования трещинПри действии внешней нагрузки в стадии эксплуатации максимальное напряжение в сжатом бетоне равно: 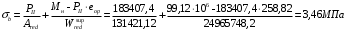 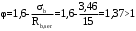 , принимаем φ = 1(п.п 4.5 /1/) , принимаем φ = 1(п.п 4.5 /1/)Расстояние от центра тяжести приведенного сечения до ядровой точки, наиболее удаленной от растянутой зоны определяется: 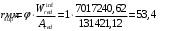 При действии усилия обжатия PI в стадии изготовления максимальное напряжение в сжатом бетоне равно: 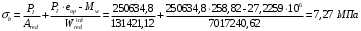 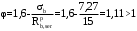 принимаем φ = 1(п.п 4.5 /1/) принимаем φ = 1(п.п 4.5 /1/)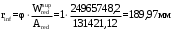 Проверяем образование верхних начальных трещин согласно п. 4.5 /3/ 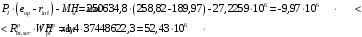 Условие выполняется – верхние трещины не образуются 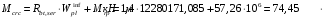 где 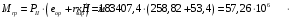 Так как Mcrc = 74,45 кНм < Mн = 99,12 кНм трещины в растянутой зоне образуются необходим расчет по раскрытию трещин. 2.8 Расчет по раскрытию трещин.Плечо внутренней пары сил при непродолжительном действии полной нагрузки вычисляется по формуле: 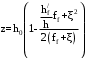 при: 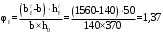 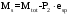 , так как усилие обжатия приложено в центре тяжести напрягаемой арматуры esp=0, тогда , так как усилие обжатия приложено в центре тяжести напрягаемой арматуры esp=0, тогда 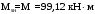 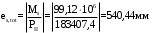 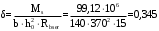 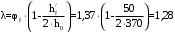 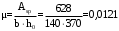 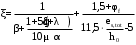 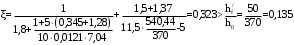 Плечо внутренней пары сил равно: 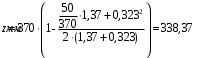 Плечо внутренней пары сил при непродолжительном действии постоянной и длительной нагрузок 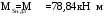 : :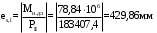 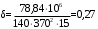 λ = 1,28; μ = 0,0121 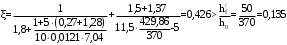 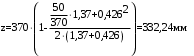 Расчет по раскрытию трещин, нормальных к продольной оси плиты Приращение напряжений в растянутой арматуре от непродолжительного действия полной нагрузки определяем по формуле 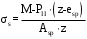 где M = Mн = 99,12 кНм; z – расстояние от центра тяжести площади сечения арматуры до точки приложения равнодействующей усилий в сжатой зоне сечения над трещиной; esp = 0, т. к. усилие обжатия приложено в центре тяжести напрягаемой арматуры 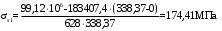 Приращение напряжений в растянутой арматуре от непродолжительного действия постоянной и длительной нагрузки M = Mн.дл = 78,84 кНм 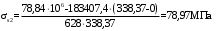 Приращение напряжений в растянутой арматуре от продолжительного действия постоянной и длительной нагрузки 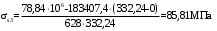 Ширину раскрытия трещин от непродолжительного действия полной нагрузки определяем по формуле 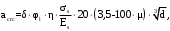 где δ – коэффициент, принимаемый для изгибаемых элементов равным 1; φl – коэффициент, принимаемый равным 1; η – коэффициент, принимаемый при стержневой арматуре периодического профиля равным 1; σ – напряжение в стержнях крайнего ряда арматуры или приращение напряжений от действия внешней нагрузки; μ – коэффициент армирования сечения; d – диаметр арматуры. 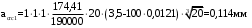 Ширина раскрытия трещин от непродолжительного действия постоянной и длительной нагрузки 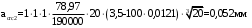 Ширина раскрытия трещин от продолжительного действия постоянной и длительной нагрузки 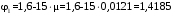 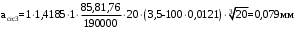 Ширина непродолжительного раскрытия трещин: 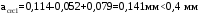 Ширина продолжительного раскрытия трещин: 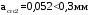 Требования к плите по трещиностойкости удовлетворяются. 2.9 Расчет прогиба плитыРасчет выполняется с учетом раскрытия трещин согласно п. 4.27 /1/ от действия постоянной и длительной нагрузок. M = Mн = 99,12 кН∙м; Nн = PII = 183,407 кН На участках, где в растянутой зоне образуются нормальные к продольной оси элемента трещины, кривизна изгибаемых элементов определяется по формуле 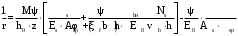 где M – момент относительно оси, нормальной к плоскости действия момента и проходящий через центр тяжести площади сечения арматуры, от всех внешних сил, расположенных по одну сторону от рассматриваемого сечения, и от усилия предварительного обжатия; z – расстояние от центра тяжести площади сечения арматуры до точки приложения равнодействующих усилий в сжатой зоне сечения над трещиной; ψs – коэффициент, учитывающий работу растянутого бетона на участке с трещинами; ψb – коэффициент, учитывающий неравномерность распределения деформаций крайнего сжатого волокна бетона по длине участка с трещинами; φf – 1,37; ξ – относительная высота сжатой зоны бетона; ν – коэффициент, характеризующий упругопластическое состояние бетона сжатой зоны; Nн – равнодействующая продольной силы и усилия предварительного обжатия. Полная кривизна для участка с трещинами в растянутой зоне определяется по формуле 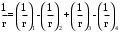 где: где: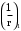 – кривизна от непродолжительного действия всей нагрузки; – кривизна от непродолжительного действия всей нагрузки;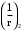 – кривизна от непродолжительного действия постоянных и длительных нагрузок; – кривизна от непродолжительного действия постоянных и длительных нагрузок; 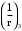 – кривизна от продолжительного действия постоянных и длительных нагрузок; – кривизна от продолжительного действия постоянных и длительных нагрузок; 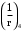 – кривизна, обусловленная выгибом элемента вследствие усадки и ползучести бетона от усилия предварительного обжатия – кривизна, обусловленная выгибом элемента вследствие усадки и ползучести бетона от усилия предварительного обжатияКривизна от непродолжительного действия всей нагрузки: 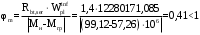 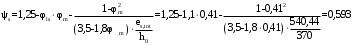 при 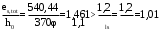 принимаем 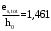 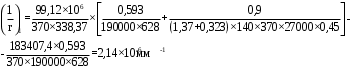 Кривизна от непродолжительного действия постоянных и длительных нагрузок: 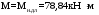 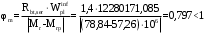 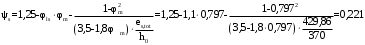 при при 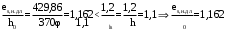 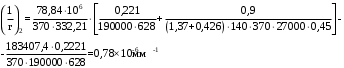 Кривизна от продолжительного действия постоянных и длительных нагрузок: 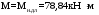 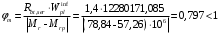 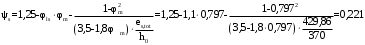 при при 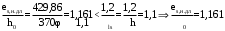 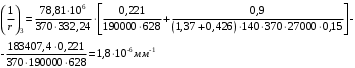 Кривизна, обусловленная выгибом элемента вследствие усадки и ползучести бетона от усилия предварительного обжатия: Определяем относительные деформации бетона, вызванные его усадкой и ползучестью от усилия предварительного обжатия: 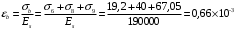 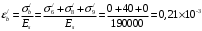 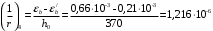 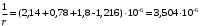 Вычисляем прогиб по формуле 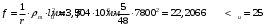 Вычисленное значение прогиба удовлетворяет требованиям. |