2 расчет и разработка технологического процесса монтажа 1 Расчет системы

• Название: 2 расчет и разработка технологического процесса монтажа 1 Расчет системы
• Дата: 16.06.2022
• Размер: 67.53 Kb.
• Имя файла: Dokument_Microsoft_Word (1).docx
• Тип: Документы; #598023

2 РАСЧЕТ И РАЗРАБОТКА ТЕХНОЛОГИЧЕСКОГО ПРОЦЕССА МОНТАЖА

2.1 Расчет системы

Основным видом течения жидкости в трубопроводах судовых систем является турбулентное. Ламинарный режим течения наблюдается в трубопроводах, транспортирующих жидкости, обладающие значительной вязкостью (мазут, масло, нефть и др.). Как известно, ламинарный режим течения наблюдается при числе Рейнольдса Re <2300, тогда как турбулентный режим при Re> 2300.

2.1.1 Определение расчетных участков трубопровода системы

Расчетная схема участка системы охлаждения показана на рисунке 2.1.

Исходные данные для расчета являются.

Скорость движения жидкости на всех участках системы охлаждения принимается v=1,85 м/с.

Материал трубопроводов системы охлаждения выполнен из углеродистой стали 20 ГОСТ 10704-91, типоразмер труб на всех участках составляет 140х4 (ДУ 125).

На рисунке 2.1 расположено три расчетных участка:

- участок 1–2 от крана запорного проходного до фильтра забортной воды включительно;

- участок 2–3 от фильтра забортной воды до электронасоса БЭН-242 включительно;

- участок 3–4 от электронасоса БЭН-242 до конденсатора включительно.



Рисунок 2.1 – Расчетная схема участка системы охлаждения

2.1.2 Определение коэффициентов сопротивления на участках системы

Рассмотрим участок 1–2 (от крана запорного проходного до фильтра забортной воды включительно).

На участке 1–2 имеются местные сопротивления. Патрубок резинокордный напорный (3 шт.) у него коэффициент сопротивления = 1,5; электронасос БЭН-240 (1 шт.) у него коэффициент сопротивления =7,5; клапан запорный (2 шт.) у него коэффициент сопротивления =2,5; колено под 90° (1 шт.) у него коэффициент сопротивления =0,2; фильтр забортной воды (1 шт.) у него коэффициент сопротивления 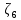=5,5.

Определим суммарные потери на участке 1–2:

;

= 22,7.

Рассмотрим участок 2–3 (от фильтра забортной воды до электронасоса БЭН-242 включительно).
На участке 2–3 имеются местные сопротивления. Патрубок резинокордный напорный (2 шт.) у него коэффициент сопротивления = 1,5; электронасос БЭН-242 (1 шт.) у него коэффициент сопротивления =7,5; клапан запорный (2 шт.) у него коэффициент сопротивления =2,5; колено под 90° (1 шт.) у него коэффициент сопротивления =0,2.

Определим суммарные потери на участке 2–3:

;

= 15,7.

Рассмотрим участок 3–4 (от электронасоса БЭН-242 до конденсатора включительно).

На участке 3–4 имеются местные сопротивления. Патрубок резинокордный напорный (1 шт.) у него коэффициент сопротивления = 1,5; клапан запорный (1 шт.) у него коэффициент сопротивления =2,5; колено под 90° (1 шт.) у него коэффициент сопротивления =0,2.

Определим суммарные потери на участке 3–4: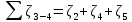

;

= 4,2.

2.1.3 Определение потерь напора на участках системы

Гидравлические потери напора по длине (путевые потери) при течении жидкости в прямой трубе обусловлены трением слоем жидкости друг о друга и о стенке канала и определяются по формуле Дарси-Вейсбоха:



(2.1)

где ∆h_mp– величина потерянного напора на прямом участке трубопровода длиной l; d – диаметр трубы, м; w – средняя скорость потока, м/с; λ – коэффициент сопротивления по длине (коэффициент сопротивления).

Как показывают опыты, коэффициент сопротивления по длине зависит от численного значения критерия Рейнольдса и относительной шероховатости стенки трубы, т.е.: λ = f(Re,ε). Здесь ε = ∆/d , где ∆ - абсолютная шероховатость, т.е. средняя высота неровностей на стенке трубы. Значение коэффициента λ определяется по эмпирическим формулам, полученным для различных областей сопротивления по кривой Никурадзе.

1. 
   Д ля ламинарного режима течения, т.е. при Re < 2320, коэффициент λ для всех труб независимо от их шероховатости определяется из точного решения задачи о ламинарном течении жидкости в прямой круглой трубе по формуле Пуазейля:
   

(4.2)

2. 
   В узкой области 2320 < Re < 3000 наблюдается скачкообразный рост коэффициента сопротивления. Эта область перехода от ламинарного режима к турбулентному характеризуется неустойчивым характером течения. Здесь наиболее вероятен на практике турбулентный режим и правильнее всего пользоваться формулами для области 3. Можно также применять эмпирическую формулу
   

λ=0,029+0,775(Re-2320)10^-5 ( 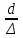2.2)

3. В области гидравлических труб при 3000 < Re < 15 толщина ламинарного слоя

у стенки δ больше абсолютной шероховатости стенок ∆, влияние выступов шероховатости, омываемых безотрывным потоком, практически не сказывается, и коэффициент сопротивления вычисляется здесь на основании обобщения опытных данных по эмпирическим соотношениям, например по формуле Блаузиуса:

(2.3)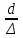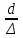



4 . В диапазоне чисел Рейнольдса 15 < R e<300 наблюдается переходная область от гидравлически гладких труб к шероховатым. В этой области (частично шероховатых труб), когда δ<∆, т.е. выступы шероховатости с высотой, меньшей средней величины ∆, продолжают оставаться в пределах ламинарного слоя, а выступы с высотой, большей средней, оказываются в турбулентной области потока, проявляется тормозящее действие шероховатости. Коэффициент λ в этом случае подсчитывается также из эмпирических соотношений, например по формуле Альтшуля:

(2.4)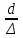



5 . При Re > 300 толщина ламинарного слоя у стенки δ достигает своего минимального значения, т.е. δ=δ_min << ∆ и не меняется с дальнейшим ростом числа Re. Поэтому λ не зависит от числа Re, а зависит лишь от ε. В этой области (шероховатых труб или области квадратичного сопротивления) для нахождения коэффициента λ может быть рекомендована, например, формула Шифринсона:

(2.5)

Принадлежности:

Прямая водопроводная труба (диаметр d = 54мм, длина l=4м) с абсолютной шероховатостью стенок ∆ (Δ=0,25 мм), смонтированная на специальной установке; дифференциальный манометр сильфонный, показывающий ДСП-780н, крыльчатый водомер типа ВВ-50; секундомер, ртутный термометр.

Описание установки.

Установка состоит из центробежного насоса 14, бака 1, трубопровода, включающего прямую горизонтальную круглую стальную трубу 2, регулировочных задвижек 11 и 13.

Потери напора в трубе измеряются дифференциальным манометром 3, присоединенным к начальному и конечному сечениям исследуемого участка трубы с помощью пьезометрических колец и импульсных трубок.

Расход, протекающий через трубопровод воды, регулируется задвижкой 11 и определяется с помощью крыльчатого водомера 4 и секундомера.

Порядок проведения опытов.

П олученные опытные значения потери давления по длине Δр_тр переводятся в напор Δh⁰_тр:

где ρ – плотность воды.

С екундный расход воды находится по формуле

где V – объем воды, протекающей за время τ.

Средняя скорость движения воды определяется из уравнения расхода: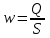







где - живое сечение потока.
Численное значение критерия Рейнольдса находится по формуле:


Значение кинематического коэффициента вязкости воды в зависимости от температуры даны в табл. 2.1.

Таблица 2.1

t, 0C	8	10	12	14	16	18	20	22	24	26	28	30
v* 104, м2/с	0,0139	0,0134	0,0124	0,0117	0,0111	0,0106	0,0101	0,0096	0,0092	0,0088	0,0084	0,0080

По найденным значениям критерия Re и шероховатости ∆ выбирается область сопротивления и по соответствующим эмпирическим формулам (2.2)-(2.5) определяется коэффициент путевых потерь λ.

Расчетное значение потерь напора по длине ∆h_тр находится по формуле Дарси-Вейсбаха (4.1).

Полученные расчетные значения путевых потерь ∆h_тр сравниваются с опытными величинами ∆р_тр.

Результаты измерений и расчетов сводятся в табл. 4.2:

Рассчитываем секундный расход воды по формуле

Q_K1 = 0, 6/80 = 0, 0075 м³/с

Q_K2 = 0, 5/74 = 0, 0068 м³/с

Q_K3 = 0, 4/62 = 0, 0065 м³/с

Q_K4 = 0, 3/60 = 0, 0050 м³/с

Q_K5 = 0, 2/51 = 0, 0039 м³/с

Q_K6 = 0, 1/34 = 0, 0029 м³/с

Рассчитываем среднюю скорость движения воды из уравнения расхода:



w₁ = 4*0, 0075/3, 14*0, 054² = 0,327 м/с

w₂ = 4*0, 0068/3, 14*0, 054² = 0,297 м/с

w₃ = 4*0, 0065/3, 14*0, 054² = 0,283 м/с

w₄ = 4*0, 0050/3, 14*0, 054² = 0,218 м/с

w₅ = 4*0, 0039/3, 14*0, 054² = 0,170 м/с

w₆ = 4*0, 0029/3, 14*0, 054² = 0,126 м/с

Рассчитываем значение числа Рейнольдса по формуле:



Re₁ = 327, 6*0, 054/0, 0111*10^-4 = 15937

Re₂ = 297, 1*0, 054/0, 0111*10^-4 = 14453

Re₃ = 283, 9*0, 054/0, 0111*10^-4 = 13811

Re₄ = 218, 4*0, 054/0, 0111*10^-4 = 10624

Re₅ = 170, 4*0, 054/0, 0111*10^-4 = 8289

Re₆ = 126, 7*0, 054/0, 0111*10^-4 = 6163

Полученные значения потери давления переводятся в напор по формуле:



∆h_тр1=9200/1000*9,8=0,938

∆h_тр2=8400/1000*9,8=0,857

∆h_тр3=6600/1000*9,8=0,673
∆h_тр4=4400/1000*9,8=0,449

∆h_тр5=2800/1000*9,8=0,286

∆h_тр6=1600/1000*9,8=0,163

Таблица 2.2

№ п/п	Δртр, Па	Δh0тр, м. вод. ст.	V, дм3	τ, с	Q*103, м3/с	w, м/с	Re	λ	∆hтр, м. вод. ст
1	9200	0,938	600	80	7,5	0,327	15937	0,0337	0,013
2	8400	0,857	500	74	6,8	0,297	14453	0,0342	0,011
3	6600	0,673	400	62	6,5	0,283	13811	0,0344	0,010
4	4400	0,449	300	60	5,0	0,218	10624	0,0356	0,006
5	2800	0,286	200	51	3,9	0,170	8289	0,0369	0,004
6	1600	0,163	100	34	2,9	0,126	6163	0,0387	0,002

Вывод:

Гидравлические потери напора по длине (путевые потери) при течении жидкости в прямой трубе обусловлены трением слоем жидкости друг о друга и о стенке канала. Как показывают опыты, коэффициент сопротивления по длине зависит от численного значения критерия Рейнольдса и относительной шероховатости стенки трубы.