МАТ_ЛОГИК. 29. Реализация конечных автоматов схемами
 Скачать 206.91 Kb. Скачать 206.91 Kb.
|
|
29.Реализация конечных автоматов схемами. Если автомат задан канонической системой булевых функций, то его можно реализовать в виде схемы из функциональных элементов и элементов задержки. Система функций реализуемых функциональными элементами предполагается полной. Эти схемы называются логическими сетями (ЛС) или синхронными логическими сетями (СЛС) или комбинационными схемами. Они строятся по тем же правилам, что и схемы из функциональных элементов, но добавляется правило введения обратной связи которое состоит в том, что в каждом контуре содержится хотя бы один элемент задержки. Опр. Состояние комбинационной схемы в момент времени t – это совокупность состояний эл. задержек. Утверждение: Произвольный конечный автомат может быть реализован в виде СЛС, причем количество элементов задержки равно наименьшему целому числу, которое превосходит log2|Q| Чтобы построить комбинационную схему из элементов данного базиса с задержками описываемую системой канонических уравнений (*), обозначим qi(t) через qi , qi(t-1) через qi * , xj(t) через xj zk(t) через zk Получим систему (**) qi = gi(x1,…,xe, q’1,…,q’r) zk = fk(x1,…,xe, q’1,…,q’r) i = 1,…r k = 1,…s Функции в правых частях системы (**) надо представить формулами над данным базисом. Строим функциональную схему из элементов данного базиса реализующую функции gi и fk (i = 1…r; k = 1…s) и имеющую входами переменные x1,…,xe , q’1,…,q’2. Затем каждому выходу qj через свой элемент задержки (зi) подаём на соответствующий вход q’j. Получим искомую комбинационную схему с задержками (или синхронную логическую схему) реализующую исходный автомат. 30.Автоматы Мура. Пусть M = {A, Q, B, G, F} – автомат Мура, т.е. у него функции выхода в канонической схеме зависят только от состояний z(t)=F(q(t-1)) и не зависит от входящего символа в данный момент времени. В случае авт. Мура в диаграмме Мура все стрелки, выходящие из состояния q помечена буквой a, той же выходной буквой, поэтому принято для этих автоматов выходную букву писать над состоянием, а не над стрелкой. Выходные буквы наз. Метками состояний. В автоматной таблице также удобнее выходные буквы располагать в отдельной строке, так как в каждом столбце, не зависимо от входного символа, выходной символ один и тот же. Простейшим автоматом Мура является задержка. Все то, что делает автомат Мили, может делать и автомат Мура. Утверждение: (теорема) Для любого автомата Мили существует, покрывающий его автомат Мура. (Т.е. существует автомат Мура, который может производить все автоматные отображения, которые производит исходный автомат. Доказательство: Допустим у исходного автомата мн. Q={q1,…,qn} A={a1,…,an}. Надо построить автомат Мура, который делает все тоже самое, что и исходный. Построим автомат Мура. M’ = { A, Q’, B, C’, F’}, у которого Q’ = {q10…qr0, q11…qr1, …, q1n...qnr} |Q’| = r + rn Функции определим следующим образом F’’(qi0) = - F’(qij) = F(aj, qi) G’(ak, qi0) = qik G’(ak, qij) = qlk, где l определяется из следующего условия: ql = G(aj, qi) Если исходный автомат находится в состоянии qi и на вход подается символ aj, то исходный автомат переходит в состояние ql = G(aj, qi). Построенный автомат Мура М’ покрывает исходный автомат М. Для всякого состояния qi автомата М, покрывающим для него состоянием является qi0 ∈Q Пусть α = ai1, ai2…ai9 ∈ A* любое входное слово F(qi, α) = ωk1, ωk2…ωk9 – выходное слово. Рассмотрим соответствующее выходное слово автомата М’, если он находится в каждый момент времени в состоянии qi0 и покажем, что эти два слова совпадают, если прочерк не учитывать. Рассмотрим работу этих автоматов. Новый автомат выдает те же самые выходные символы, что и исходный, но с задержкой на один такт. 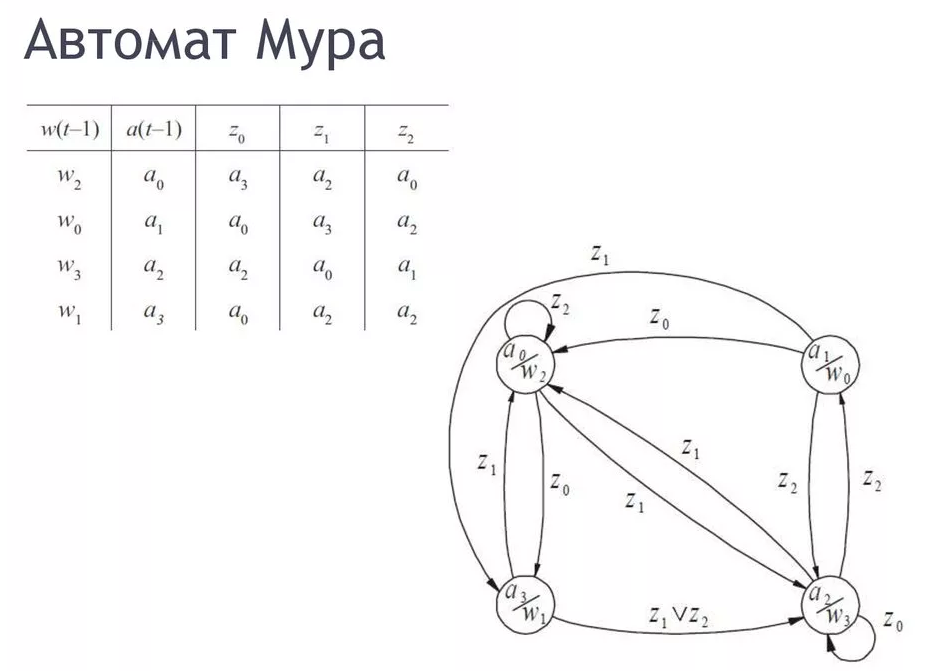 31.Основные соединения автоматов. Тривиальные параллельные соединения автоматов — это совокупность 2х автоматов с независимыми входами и выходами. Если M1 = { A1, Q1, B1, C1, F1, G1 } M2 = { A2, Q2, B2, C2, F2, G2 } то у автомата М входной алфавит А = А1×А2, B = B1×B2, Q = Q1×Q2 Параллельное соединение автоматов, когда M1 = {A, Q1, B1, C1, F1, G1} M2 = {A, Q2, B2, C2, F2, G2} у М : B = B1×B2, Q = Q1×Q2 Последовательные соединения. A=A1; B=B2; Q=Q1×Q2 Соединения с обратной связью. Имеется некоторый автомат М1 и автомат Мура М2. Некоторый вход у автомата М1 является выходом автомата Мура М2 и наоборот. Замечание. Возможны модификации, при которых происходит более мелкое разбиение алфавитов. Синхронной сетью автоматов ССА называется схема, использующая указанные соединения, причем в каждом контуре этой схемы должен быть хотя бы один автомат Мура. Он играет роль линии задержки. В частности, СЛС является примером ССА. Триггеры: Автомат Мура называется полным (или совершенным), если возможны переходы из любого его состояния в любое другое с помощью подходящей входной буквы, и разные состояния дают различные выходы. Полный автомат Мура с двумя состояниями называется триггером. F(q) ≡ q 1.D-триггер (линия задержки) . RS -_триггер. JK- триггер. D-триггер
RS -_триггер Таблица 1
JK- триггер Таблица 2
Так как разные состояния полного автомата Мура дают различные выходы, то можно считать, что между алфавитом состояний Q и выходным алфавитом B имеются взаимооднозначные соответствия. Поэтому можно считать, что алфавит Q и B совпадают . Отождествив соответствующие буквы алфавитов. Тогда F(q)=q, то есть функция выходов будет тождественной и в определении полного автомата Мура может не указываться. |
