3 дарис пахт 22. 3 Дріс. Гидродинамика. Аын сипаттамалары Сйыты аыныны трлері Гидродинамика
 Скачать 176.84 Kb. Скачать 176.84 Kb.
|
|
3 Дәріс. Гидродинамика. Ағын сипаттамалары Сұйықтық ағынының түрлері Гидродинамика (гидро... және динамика) -гидроаэромеханиканың сығылмайтын сұйықтықтың қозғалысын және оның өзімен шекаралас орналасқан қатты денемен әсерлесуін зерттейтін бөлімі. Гидродинамика-сұйықтық пен газ механикасының ертеден келе жатқан әрі жақсы дамыған саласы. Гидродинамика көмегімен сұйықтықтың жалпы қасиеттеріне механиканың негізгі заңдары мен тәсілдерін қолдана отырып, сұйықтық алып жатқан тұтас ортаның кез келген нүктесінің жылдамдығы, қысымы тәрізді өлшемдер анықталады. Гидродинамиканың негізгі тәсілдері дыбыс жылдамдығынан (шамамен 330 м/сx1200 км/сағ) жылдамдығы төмен газ қасиеттерін зерттеу үшін де пайдаланылады. Гидродинамика теория гидродинамика және эксперименттік гидродинамика болып екіге бөлінеді. Теориялық гидродинамикада сұйықтықтың жеке бөлшектері сұйық орналасқан тұтас ортаның материалдық нүктелері ретінде қарастырылады немесе сұйықтық алып жатқан кеңістіктегі жылдамдықтар өрісі зерттеледі. Гидродинамика тұрғысынан алғанда сұйықтықтың ең басты қасиеті – аққыштық пен тұтастық. Сұйықтықтың газ тәріздес ортадан негізгі айырмашылығы – оның сығылмайтындығы. Мұндай сұйықтықтар үшін үзіліссіздік теңдеуі мен Навье-Стокс теңдеуі қолданылады. Тұтқыр сұйықтық қозғалысы қарастырылғанда, ағыс сипаттамасы болып табылатын өлшемсіз шама -Рейнольдс саны қолданылады. Эксперименттік гидродинамика тәсілдерінің қатарына сұйықтық қозғалысы мен оған шекаралас орналасқан қатты дене маңындағы ағысты кішірейтілген масштабта қайта жасап алуға негізделген модельдеу тәсілдері жатады. Гидродинамиканың көптеген есептерін шешуге ұқсастық теориясы мен ұқсастық өлшеміне негізделген гидродинамикалық тәжірибелер де қолданылады. Гидродинамика әдістері гидравлика, гидрология және гидротех. есептерін шығаруды, гидротурбинаны, сорғыларды, құбырларды, т.б. есептеуді табысты шешуге мүмкіндік береді. Гидродинамика дегеніміз -сұйық қозғалысының заңдылығын және сұйықтық қатты денемен ағу кезіндегі байланысын, сұйық ішіндегі қысымды зерттейтін гидравликаның негізгі бір бөлімі. Осыған байланысты сұйық механикасының ішкі және сыртқы есептері деген ұғым енгізіледі. Ішкі есептеріне құбырдағы, ашық арықтағы сұйық қозғалыстары, т.б. жатады. Сыртқы есептеулеріне сұйықтың қатты денені айналып ағу түрлері жатады. Гидравлика саласы -сұйық кинематиканы динамикамен бірге қарастырады да, оның айырмашылығын, түрлерін зерттеумен қатар сұйық кинематикалық сипаттамаларына түскен күштерді есептемегендегі сұйық қозғалысын, ал сұйық динамикасы сұйық қозғалысына түсетін күштердің байланыстылық заңдылығын зерттейді. Гидравликалық сұйықты үздіксіз орта ретінде қарайды да, оның барлық кеңістіктігінде толық толтырады. Көбінесе гидродинамикалық есептерді шешкен кезде сұйықтың қозғалуы, оған түсетін сыртқы күштермен қатар салмақ күші, сыртқы күштермен қатар салмақ күші, сыртқы қысым, т.б. күштер белгілі болады. Сұйық қозғалысын түсіндіретін белгісіз факторларға ішкі гидродинамикалық қысым және кейбір кеңістіктегі әрбір нүктедегі сұйық жылдамдығының ағуы жатады. Гидравликалық қысым әр нүктеде оның координатының функциясы болып табылады, сонымен қатар уақыт аралығында өзгеруінен, ол уақыт функциясы t болады. Сұйық қозғалысының заңдылығын зерттеудің қиындығы, оның табиғатында және ең қиыны ондағы жанама кернеу күшті есептеу, ол бөлек сұйық, яғни үйкеліс күшін ескермей, сонан кейін жасалған теңдеуге өзгеріс енгізу арқылы, нақтылы сұйықтың үйкеліс күшінің әсерін еске алу ( 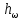 ). ).Гидродинамиканың негізгі түсініктері: Гидродинамиканы үйренуде негізгі объектілердің бірі сұйық ағыны, яғни шекттеулі беттіктері арасында сұйық массасының қозғалысы болып табылады. Сұйық әр түрлі күштер әсерінен қозғалады: ауырлық күшінің; ішкі қысым; инерциялы күш және т.б. Сұйықтың қозғалыс заңдарын оқып үйренуде екі түрлі есеппен түйісу керек болады: 1)сыртқы есеп, сұйық ағынының гидродинамикалық сипаттамалары көрсетілген, сұйықты айнала ағатын денеге салынған күшті табу керек. 2)ішкі есеп, сұйыққа әсерін тигізетін күштер берілген, ағынның гидродинамикалық сипаттамаларын табу керек. Ағынның гидродинамикалық сипаттамалары болып: -гидродинамикалық қысым; -сұйық қозғалысының жылдамдығы. Гидродинамикалық қысым -сұйықтың қозғалысы кезінде дамитын ішкі қысым. Берілген нүктеде сұйық қозғалысының жылдамдығы -берілген нүктеде орналасқан, сұйық бөлшектерінің кеңістікте ауысу жылдамдығы. Жылдамдық бірлік уақыт ішінде сұйық бөлшегінің жүріп өткен жолының ұзындығымен анықталады. 2. Сұйықтық қозғалысының режімдері мен түрлерінің классификациясы: Сұйықтық ағысының екі режимі бар: ламинарлы, өтпелі және турбелентті. Ламинарлы ағыс (қабаттық, реттелген) -сұйықтықтың жеке қабаттары бір-біріне қатысты араласпай жылжығандағы қозғалыс. Тұтқыр сұйықтықтар  (майлар) көбінесе реттеліп қозғалады. (майлар) көбінесе реттеліп қозғалады.    Турбуленттік ағыс (реттелмеген) – сұйықтық бөлшектерінің әрдайым траекториясы өзгеріп тұратын және қарқынды араласу жүретін күрделі қозғалыс. Көбінесе тұтқырлығы аз сұйықтықтар (су, ауа) ретсіз қозғалады. Құбырдағы сұйықтық ағынының күйі (режимі) тұтқырлық күшін сипаттайтын Рейнольдс саны келесі формуламен анықталады: мұндағы Дөңгелек ағысты құбырлар үшін Дөңгелек ағысты құбырлар үшін Рейнольдс саны келесі формуламен анықталады: Барлық басқа көлденең ағыстар үшін (сонымен қатар ашық арналар үшін) Рейнольдс саны келесі формуламен анықталады: мұндағы Сұйықтық қозғалысының бірнеше түрін атауға болады: орныққан және орнықпаған; бірқалыпты және бірқалыпсыз; арынды және арынсыз. Орныққан қозғалыс -уақыт өтуіне байланысты кез келген нүктедегі ағын жылдамдығы мен гидродинамикалық қысым өзгермей, ал тек қана сұйықтық ағынындағы қарастырылып отырған нүкте орнына тәуелді, яғни оның координаталарының функциясы болып табылатын сұйықтық қозғалысы. Мысалы, тұрақты арындағы резервуар саңылауынан сұйықтықтың ағуы, каналдағы өзгермейтін көлденең қималы және тұрақты тереңдіктегі су ағыны. Орнықпаған қозғалыс -уақыт өтуіне байланысты әр нүктедегі ағын жылдамдығы мен қысымы өзгеретін сұйықтық қозғалысы. Мысалы, айнымалы арын кезінде резервуар саңылауынан сұйықтық ағуы. Бірқалыпты қозғалыс -ұзындығы бойынша нақты ағыстар мен ағын жылдамдығы өзгермейтін сұйықтықтың орныққан қозғалысы. Мысалы, өзгермейтін қималы және тұрақты тереңдіктегі құбыр немесе каналдағы сұйықтық қозғалысы. Бірқалыпсыз қозғалыс -ұзындығы бойынша нақты ағыстар мен ағын жылдамдығы өзгеретін сұйықтықтың орныққан қозғалысы. Мысалы, конустық құбырда және табиғи арнадағы сұйықтықтың қозғалысы. Арынды қозғалыс -құбыр өткізгіштің барлық көлденең қимасы атмосфералықтан жоғары қысыммен толтырылатын сұйықтық қозғалысы: сұйықтық қозғалысы қысым күштері арқасында жүзеге асады, яғни қосымша энергия шығынын тудырытын арын арқасында. Арынсыз қозғалыс -атмосфералық қысымның астында орналасқан бос беті бар ағындағы сұйықтық қозғалысы. Сұйық қозғалысын зерттеудің екі әдісі бар, олар: Ж. Лагранж бен Л. Эйлер әдістері. Ж. Лагранж әдісі -сұйықтың әрбір бөлшектерінің қозғалысын зерттеу, яғни оның қозғалысының траекториясы. Бұл тәсілдің өте қиындығы – көп тарамағандығы, соның кесірінен практикада көп қолданылмайды. Л. Эйлер әдісінің ерекшелігі -белгілі уақыттағы барлық сұйық қозғалысының кеңістіктегі, әр түрлі нүктедегі жағдайын зерттеу. Ал артықшылығы -кеңістіктегі қай нүктеде де болсын, қай уақытта да сұйық қозғалысының жылдамдығын табуға болады, яғни жылдамдық белдеуін тұрғызу бейнеленеді де, сұйық қозғалысының жылдамдығын табуға болады, яғни жылдамдық полясын тұрғызу бейнеленеді де, сұйық қозғалысын зерттеген кезде бұл тәсіл кеңінен қолданылады. Эйлер тәсілінің кемшілігі -жылдамдық ауқымын қарастырған кезде әрбір сұйық бөлшектерінің траекториясын тексермейді. Сұйық қозғалысының түрлері Сұйықтың ағынын зерттеу үшін қажетті кинематикалық үлгіні таңдап алу керек. Мұндағы сұйық ағынының табиғи заңдылығын зерттеудің қиындығын, оның ағу табиғатында және ондағы бөлшек арасындағы үйкеліс кедергісінің әсерінен жанама кернеу күшті есептеудің қиындығында. Бұл мәселені шешу үшін Л. Эйлер әдісін пайдаланамыз. Ол үшін, сұйық бөлшектерінің үйкеліс күшін ескермей (идеалды сұйық) теңдеу құру, арқылы есептеп, содан кейін осы теңдеуді тұтқырлық реалды сұйыққа ыңғайлап, ондағы үйкеліс кедергісінің әсерін еске алады. Сұйық қозғалысын зерттеу үшін Эйлер әдісімен танысамыз. Қимылсыз координата жүйесін таңдап алып, оны сұйық қозғалысының жылдамдығына жатқызамыз. Ағын ішіндегі нүктедегі жылдам (мгновенный) шама құратын жылдамдық координата осіндегі нүктенің орналасуына байланысты болады (3.14-сурет), яғни нүктенің орналасу координаты x, y, z және уақыт ішіндегі (t) жағдайына байланысты. Қаралып отырған М нүктесіндегі сұйық ағынның жергілікті жылдамдығын құраушы 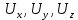 . . 3.14-сурет. Координата жүйесіндегі жергілікті жылдамдық. Бұлардың функционалды жылдамдығын былай жазамыз: 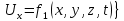 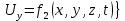 (3.59) (3.59) Осы функциялардың нақтылы жағдайдағы ағын шамасын білсек, онда кез келген уақыттағы сұйық ағынның бөлініп таралуын білуге болады. Лагранж әдісін пайдалансақ онда,белгіленген нүктенің сұйықпен бірге жылжу кезіндегі координатасын x, y, z белгілеп, оның кинематикасын зерттейміз. Ол үшін, ағын ішіндегі нүктені қимылсыз координата жүйесімен белгілеп, олардың координатасын  деп, уақыт кезеңінен деп, уақыт кезеңінен  . Сонда, сұйық ішіндегі белгіленіп алынған нүктенің траекториядағы қимыл – қозғалысы бір–бірінен айырмашылығы бастапқы координаталарының тұрған шамасына байланысты. Әрбір қаралып отырған нүктенің координатасы үшін олардың функционалды тәуелділігі бар: . Сонда, сұйық ішіндегі белгіленіп алынған нүктенің траекториядағы қимыл – қозғалысы бір–бірінен айырмашылығы бастапқы координаталарының тұрған шамасына байланысты. Әрбір қаралып отырған нүктенің координатасы үшін олардың функционалды тәуелділігі бар:   (3.60) (3.60)Осы нүктелердің жылжу жылдамдығы ағынның жергілікті жылдамдығымен сәйкес келеді: 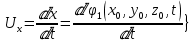 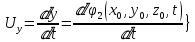  (3.61) (3.61)Лагранж әдісі бойынша сұйықтың және нүктелердің t уақыт ішіндегі кеңістіктегі өз траекториясымен ағып өтуін сипаттайды да, сұйықтағы нүктенің осыдан t уақыт бұрын қай жерде болғанын және t уақыттан кейін қай жерде болатынын да анықтауға болады. Сұйық ішіндегі барлық нүктелердің траекторияларын анықтайтын теңдеулерді жазу өте қиын болғандықтан, Лагранж әдісін гидродинамикада тіптен пайдаланбайды. Көбінесе, Эйлер әдісін қолданады. Сұйық қозғалысының түрлерін қарастырамыз, олар сұйық ағынының қалыптасқан (тұрақты) және қалыптаспаған (тұрақсыз) болып бөлінеді. Қалыптасқан қозғалыс деп ағынның қай нүктесіндегі болсын, сұйықтың тереңдігі, жылдамдығы және қысым уақыт аралығындағы өзгермеуін айтады, яғни 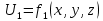 және және 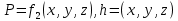 уақытқа байланысты болмайды. уақытқа байланысты болмайды.Мысалы, тұрақты қозғалысқа бензин багінен аққан жанармайды жатқызуға болады, егер оның деңгейі өзгермей аққан кездегі күйі, сонымен қатар тоғандағы су қозғалысы, сондықтан оның геометриялық көрсеткіштері көлденең қимасы мен тереңдігі тұрақты болуы керек. Қалыптаспаған сұйық ағыны деп ағынның кеңістіктегі қай нүктесінде болсадағы сұйықтың жылдамдығы мен қысым уақыт аралығында өзгеріп отыратын қозғалысын айтады. Кейбір, жалпы жағдайда қалыптасқан ағынның тереңдігі қысым және жылдамдығының координатасы уақытына байланысты болады. Қалыптаспаған қозғалыста ағыс сызығы уақыт ішінде өзгеріп отырады. Ағынның барлық нүктелерінде бір сәтте жүргізілген жылдамдық векторлары орталық сызыққа жанама болып бағытталуын қисық сызықты ағыс сызығы деп атайды (3.15-сурет).  3.15-сурет. Ағын нүктелерінде бір сәтте жүргізілген жанама вектор жылдамдығы. Егер ағын қозғалысы белгіленген нүктелердегі ағынның жылдамдығы бағыты уақыт аралығында өзгереді. Ағыс ішіндегі нүктенің x, y, z координатасының құраушы жергілікті жылдамдығы координата осінің бойымен 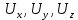 болады. Ағыс сызығы бойымен ауысқандағы арақашықтығын ds деп, нүктелерінің координатасын x+dx, y+dy және z+dz болса: болады. Ағыс сызығы бойымен ауысқандағы арақашықтығын ds деп, нүктелерінің координатасын x+dx, y+dy және z+dz болса: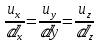 бұл теңдеу ағыс сызығының теңдеуідеп аталады. Қозғалыстағы сұйық ағыны тұйық контур жүргізін, ондағы шексіз элементарлы кішкене алаңшаның жазықтықпен шектелген жеріндегі нүктелеріне ток сызығын жүргізсек, түтікті көрінбейтін жазықтық ток түтігі деп атайды. Ток түтігі мен шектелген сұйық бөлшектерінің массасын элементарлы сұйық ағыншасы деп атайды. Барлық элементарлы сұйық ағыншаларының әр түрлі жылдамдықта болып ағуын сұйық тасқыны (ағыны) дейді. Сұйық ағыншасы үшке бөлінеді: а) еркін ағыс деп үш жағынан ағын арнасына тірелген, ашық бетті су қозғалысын айтады. Мұндағы ағын тек салмақ күштерінің жанама (τ) әсерінен қозғалады; ә) тегеурінді ағын деп жан-жағынан арнаға тірелген ағысты қысымды айтады. Ағынның қозғалысы қысым күшінің әсерінен болады (құбырдағы ағын); б) арнасыз ағын деп жан-жағы газбен немесе сұйықпен қоршалған ортада ағуын айтады. Кейде оны гидравликалыұ ағынша деп те атайды. Сұйық тасқынының гидравликалық элементтері: Сұйық шығыны және орташа жылдамдығы. Сұйық қозғалысының гидравликалық көрсеткіштеріне траектория туралы ұғымнан басқа ток сызықтары, элементарлы ағыншалар, тасқын, ағынның көлденең қимасы, тоғанның ылғалданған периметрі, гидравликалық радиус, сұйықтың шығыны мен орташа жылдамдығы жатады. Көлденең қимасы (ω) деп ағын бағыты мен барлығ ток сызықтарында перпендикуляры көлденең қима ауданын айтады. Мысалы, дөңгелек құбырдың диаметрі d суға толы барлық қимасының дөңгелек ауданында тең болады, яғни  Ағын қимасының ауданы мен жылдамдығының көбейтіндісін сұйықтың немесе газдың элементарлы шығыны деп атайды.  (3.62), (3.62),мұндағы, U – сұйықтың жергілікті жылдамдығы, м  с; с;  -элементарлы көлем. -элементарлы көлем.Белгілі уақыт ішінде сұйық қимасынан ағып өтетін сұйық массасын: 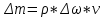 (3.63) (3.63)формуласымен есептейді. Ал қима ауданы ω ағыншалардың қимасының жиынтығына тең болады: 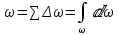 (3.64) (3.64)Сұйықтың шығыны ( 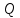 ) деп барлық элементарлы ағыншалардың жиынтығын айтады: ) деп барлық элементарлы ағыншалардың жиынтығын айтады: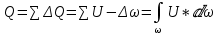 (3.65) (3.65)Сұйықтың массалық шығыны(m) -олардың әрбір элеменарлы ағыншалардың массалық шығынының жиынтығына тең болады: 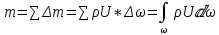 (3.66) (3.66)Ылғалданған периметр (  ) – сұйықтың көлденең қимасының периметрінің қатты қабырғамен жұғысқан жері. Мысалы, дөңгелек құбырдың толық қимасымен сұйықтың аққан кездегі ылғалданған периметрі құбырдың шеңберінің ұзындығына тең, яғни ) – сұйықтың көлденең қимасының периметрінің қатты қабырғамен жұғысқан жері. Мысалы, дөңгелек құбырдың толық қимасымен сұйықтың аққан кездегі ылғалданған периметрі құбырдың шеңберінің ұзындығына тең, яғни  . .Гидравликалық радиус (R) – құбырдың көлденең қимасының ауданының, ылғалданған периметрінің қатынасына тең:  (3.67) (3.67)Мысалы, құбырдағы сұйықтың толық қимасымен аққандағы гидравликалық радиус, оның диаметрінің төрттен біріне тең:   Сұйық ағынның ортша жылдамдығы сұйық шығыны қима ауданының қатынасына тең болады: 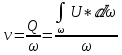 , ,бұдан 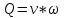 (3.671) (3.671)Сұйықтың үздіксіздік-дифференциалды теңдеуі: Үздіксіз ағындар деп ағысы үзілмей, арна кеңістігін толық толтырып ағатын ағындарды айтады. Бұл жағдайда козғалыстағы сығылмайтын сұйық шамасының сандық (не үлкейтіп, не кішірейтпейді) уақыт аралығында өзгермейді. Элементарлы параллелепипедтің қырынан (жанына) ағып өтетін сұйық массасын қарастырамыз. (3.16-сурет).  3.16-сурет. Сұйықтың үздіксіздік-дифференциалды теңдеуін дәлелдеу. Параллелепипедтің сол жақ қырынан ағып кіретін сұйықтың жылдамдығын 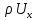 , ал оң жақ қырынан ағып шығатын жылдамдығын , ал оң жақ қырынан ағып шығатын жылдамдығын деп белгілейді. Ағын ішінен x, y, z координатты нүктені таңдап алып, O’ нүктесіндегі сұйық ағынның жылдамдығын құраушы 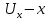 осі бойымен, осі бойымен, 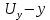 осі бойымен және осі бойымен және  осі бойымен өтеді. Параллелепипедтің осі бойымен өтеді. Параллелепипедтің  элементарлы ауданшасының O1 нүктесіндегі уақыт аралығын (dt) белгілейді. Сонымен параллелепипедтің ішіне элементарлы ауданшасының O1 нүктесіндегі уақыт аралығын (dt) белгілейді. Сонымен параллелепипедтің ішіне  сұйық массасы ағып кіреді. Параллелепипедтің сол жақ қырынан O’ нүктесінен dt уақыт аралығында сұйық массасы ағып кіреді. Параллелепипедтің сол жақ қырынан O’ нүктесінен dt уақыт аралығында  көлемінен O” нүктесіне жетеді де көлемінен O” нүктесіне жетеді де  координатасында болады, ал ағып шыққан сұйық массасының көлемін былай табады: координатасында болады, ал ағып шыққан сұйық массасының көлемін былай табады: (3.68) (3.68)Демек, сұйық аққан кезде құраушы жылдамдығы  нүктесіндегі параллелепипедтің сұйық массасы нүктесіндегі параллелепипедтің сұйық массасы  , ал оның ауданы , ал оның ауданы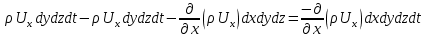 шамасына өзгереді. Параллелепипедтің басқа қырынан 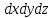 көлемді. Сұйық осыған ұқсас өзгереді, оны былай табады: көлемді. Сұйық осыған ұқсас өзгереді, оны былай табады: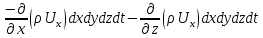 (3.69) (3.69)Сұйық массасының өзгеруін жиынтығын (суммасы) белгіленген 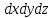 ауданын ауданын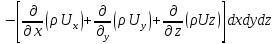 арқылы табады. Сұйық ауданының тығыздығы 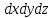 ауданымен шектелген ауданымен шектелген 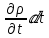 өзгеруі мүмкін, ол оның масса осы ауданда өзгеруі мүмкін, ол оның масса осы ауданда 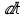 уақыт аралығында уақыт аралығында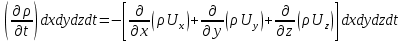 болады. 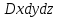 шамасы теңдеудің екі жағында да бар, оны есептемесек, белгілі нүктедегі ағынның тоқтаусыз ағу шарты бойынша: шамасы теңдеудің екі жағында да бар, оны есептемесек, белгілі нүктедегі ағынның тоқтаусыз ағу шарты бойынша: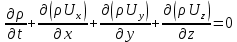 (3.70) (3.70)болады. Бұл теңдеуді гидромеханикада сұйықтың үздіксіз ағу теңдеуі деп атайды. Егер ағын қалыптасқан қозғалыс түрінде болса  онда теңдеу (1.70), былай жазылады: онда теңдеу (1.70), былай жазылады: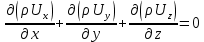 (3.701) (3.701)Егер сұйық сығылмайтын болса, яғни 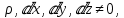 онда онда (3.702) (3.702)(3.70) теңдеуді сұйықтың үзілмеушілігінің дифференциалды формадағы сығылмайтын, өз бетімен аққан суға арналған тендеуі деп атайды (JI.Эйлер теңдеуі). Сығылмайтын сұйықтың потенциалды қозғалысы үшін, функция  – потенциалды жылдамдығы дейді, жеке туындылардың (производный) координатадағы осі тең болады, олардың сәйкестелген жылдамдық проекциясына – потенциалды жылдамдығы дейді, жеке туындылардың (производный) координатадағы осі тең болады, олардың сәйкестелген жылдамдық проекциясына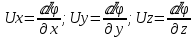 келеді. Осыған қарағанда үздіксіз ағу теңдеуін (3.70) былай жазады:  (3.71) (3.71)Бұл теңдеуді (3.71) Лаплас теңдеуі дейді. Сұйық ағынындағы көлденең қималар 1-1, 2-2, 3-3 (3.18-сурет) бұлардың әрқайсына мына теңдеу сәйкес келеді. Барлық ағын қималарындағы Q = const; онда 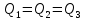 және және 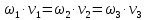 (3.72) (3.72)Бұл теңдеу сығылмайтын сұйықтағы үздіксіз ағу теңдеуіне жатады. Бақылау сұрақтары: 1) Гидродинамиканың зерттеу объектісі және оның негізгі мақсаты. 2) Сұйықтың бірқалыпты және бірқалыпсыз қозғалысы анықтамасы. 3) Қимыл, қима дегенді қалай түсінесіз және оның үш көрсеткіштерін (ауданына, ылғалданған периметріне және гидравликалық радиусына) түсіндіріп жазыңыз. 4) Гидравликалық радиус деген не? 5) Су өтіміне және ағынның орташа жылдамдығына анықтама беріңіз, өлшем бірлігін атаңыз. 6) Үздіксіз ағындар дегеніміз не? ГЛОССАРИЙ 1) Кинематика -механиканың, дене қозғалысының геометриялық қасиеттерін, олардың массасы мен әсер етуші күштерді ескермей зерттейтін бөлімі. Классикалық механиканың бөлімі. Кинематика -механика, движение тела без геометрических отдел. Кафедра классической механики. 2) Динамика -механиканың түсірілген күш әсерінен материалдық денелердің қозғалысын зерттейтін бөлімі. Динамиканың негізі -механиканың Ньютон заңдары. Динамика -представляет собой раздел механики, который исследует движение материальных тел под действием силы. Основа динамика -закон Ньютона. 3) Траектория -материялық нүктенің өз қозғалысы кезінде сызатын біртұтас сызығы. Траектория -материальной точки его движения в гильзе одной линии. 4) Дифференциал -айналдырушы иінді күшті жетектегі екі білік арасында берілген қатынаста бөліп, олардың әртүрлі бұрыштық жылдамдықпен айналып қозғалуын қамтамасыз ететін күштік берілістің механизмі. Дифференциал -преобразование коленчатого сильной связь между этими двумя на ведущем валу, выделяя их различную угловую скорость, которая обеспечивает вращательное движение механизма передачи мощности. 5) Потенциал -физикалық күш өрістерінің кең көлемді тобын және физикалық шамалардың вектормен көрсетілген өрістерін сипаттайтын ұғым. Потенциал -это концепция, которая описывает большую группу полей физической силы и полей, обозначенных вектором. |
