3. Гидродинамические расчеты отборов жидкости и забойных давлени. 3. Гидродинамические расчеты отборов жидкости из залежи и забойных давлений при жестком водонапорном режиме
 Скачать 351.1 Kb. Скачать 351.1 Kb.
|
|
3. Гидродинамические расчеты отборов жидкости из залежи и забойных давлений при жестком водонапорном режиме 3.1. Полосовая залежь Расчёт дебитов рядов скважин, суммарных отборов жидкости из пласта, а также определение давлений на забоях скважин при одновременной работе нескольких рядов связаны со значительными математическими трудностями. В связи с этим при решении задач по определению дебитов скважин, отборов отдельных блоков и суммарной добычи жидкости из залежи пользуются методом электродинамических аналогий. Рассмотрим приток жидкости к прямолинейной цепочке скважин, расположенных на расстоянии 2Ϭ друг от друга и на расстоянии L от контура питания. Пусть на контуре питания задан постоянный потенциал Фк, на забоях скважин – потенциалы Фс. 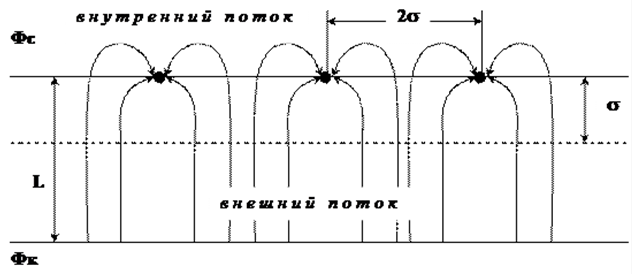 Результаты решения показывают, что на расстоянии от контура питания до половины расстояния между скважинами движение жидкости практически прямолинейное, и падение потенциала (давления) на этом участке происходит по закону прямолинейной фильтрации. Вблизи каждой скважины характер движения близок к плоскорадиальному. Пусть залежь эксплуатируется одним рядом скважин на жёстком водонапорном режиме (рис. 3.1), то есть соблюдается равенство отобранных и закачанных объемов жидкости. 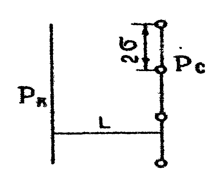 Рис. 3.1. Схема эксплуатации одного ряда скважин На контуре питания, расположенном параллельно ряду, поддерживается давление РК. Забойное давление в добывающих скважинах РС, расстояние между скважинами одинаково и равно 2, расстояние между контуром питания и рядом скважин L, длина ряда В. Метод эквивалентных фильтрационных сопротивлений ЭГДА предложен Ю.П. Борисовым и основан на аналогии движения жидкости в пористой среде с течением электрического тока в проводниках. Закон Ома: U=I∙R. Закон фильтрации жидкости: ∆P=Q∙Rг. Аналогия между гидродинамическими и электрическими процессами проявляется в следующем: 1) изменение напряжения U между узлами электрической сетки аналогично распределению давления в пласте ∆P: 2) электрическое сопротивление участка электрической сетки R пропорционально (аналогично) гидродинамическому сопротивлению участка моделируемого пласта Rг: 3) сила тока, протекающего между узлами сетки I, пропорциональна (аналогична) количеству жидкости Q, протекающей через участок моделируемого пласта: При этом справедлив 1 закон Кирхгофа, согласно которому алгебраическая сумма токов ветвей, сходящихся в каждом узле цепи, равна нулю. I1 - I2 - I3=0. 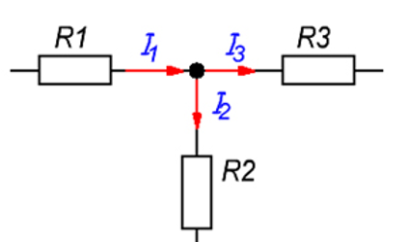 Сумма всех токов, втекающих в узел, равна сумме всех токов, вытекающих из узла. При суммировании токов принято брать положительный знак, если ток идёт по направлению к узлу, и отрицательный знак, если ток идёт в противоположную от узла сторону. С помощью метода эквивалентных фильтрационных сопротивлений ЭГДАЮ.П. Борисова легко составить уравнения для расчета дебитов и давлений на забоях скважин, расположенных в виде прямолинейных цепочек или кольцевых батарей. Дебит одной скважины, работающей в единственном бесконечном ряде в полосовой залежи при равных вязкостях воды и нефти, можно определить по формуле 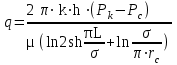 (3.1) (3.1)где k – коэффициент проницаемости пласта; h – толщина пласта; РК – давление на контуре питания залежи; РС– забойное давление в скважине; – динамическая вязкость жидкости; L – расстояние между контуром питания и рядом; 2 – расстояние между скважинами; r – радиус гидродинамически совершенной скважины, sh- гиперболический синус. Если 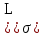 , что практически всегда имеет место, то формула (3.1) существенно упрощается, так как можно принять , что практически всегда имеет место, то формула (3.1) существенно упрощается, так как можно принять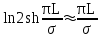 . .Подставив это значение в формулу (3.1) и умножив числитель и знаменатель на /, получим  . (3.2) . (3.2)Поделив формулу (3.2) на расстояние между скважинами 2, получим удельный дебит скважины, приходящийся на единицу расстояния между скважинами: 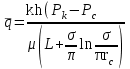 (3.3) (3.3)Суммарный дебит всех скважин, работающих в ряду Q, будет равен произведению 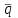 на ширину галереиB (ряда), то есть на ширину галереиB (ряда), то есть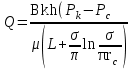 . (3.4) . (3.4)Решив уравнение (3.4) относительно разности давлений между пластом и скважиной, получим  . (3.5) . (3.5)Комплекс параметров 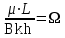 принято называть внешним сопротивлением ряда, принято называть внешним сопротивлением ряда, 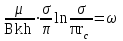 – внутренним сопротивлением призабойной зоны скважины. – внутренним сопротивлением призабойной зоны скважины.Внешнее сопротивление Ω – это сопротивление между рядами Внутреннее сопротивление ω – это сопротивление между скважинами в рядах. С учётом принятых обозначений формула (3.5) запишется в виде 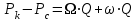 (3.6) (3.6)По аналогии с законом Ома ∆U=I ∙ R, ∆P=Q (Ω+ω) Использование формулы (3.6) для определения дебитов рядов скважин и забойных давлений существенно сократит трудоёмкость расчётов. Пусть залежь эксплуатируется одним рядом скважин на жестком водонапорном режиме, т.е. из пласта отбирается столько же жидкости, сколько поступает через контур питания (рис. 3.2). На контуре питания, расположенном параллельно ряду, поддерживается давление Pк. Забойное давление в добывающих скважинах Pс, расстояние между скважинами одинаково и равно 2Ϭ, между контуром питания и рядом скважин равно L, длина ряда B. 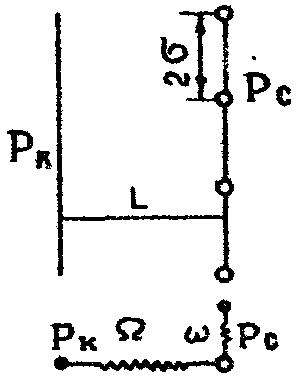 Рис. 3.2. Схема эксплуатации одного ряда скважин Суммарный дебит всех скважин ряда определяется по формуле 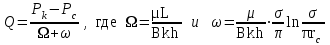 (3.7) (3.7)(по аналогии с законом Ома I=U/R). Дебит одной скважины находим путём деления дебита ряда на количество скважин: 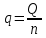 По аналогии с электрической схемой, легко написать систему уравнений для двух рядов добывающих скважин (рис. 3.3): 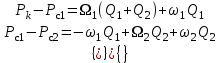 (3.8) (3.8)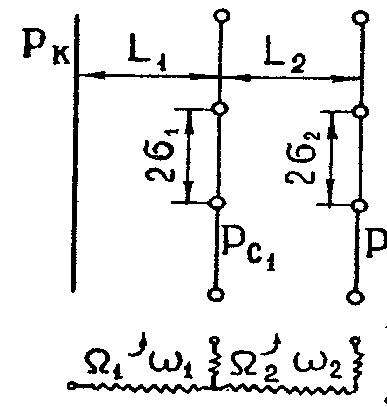 Рис.3.3. Схема эксплуатации двух рядов скважин Используется 2-й закон Кирхгофа – сумма ЭДС в замкнутом контуре равна сумме падения напряжения на всех сопротивлениях. Падение напряжения на резисторе положительно, если направление тока в нем совпадает с направлением обхода. Это правило используем для потока жидкости. В системе уравнений (3.8) четыре неизвестных: РС1, РС2, Q1 и Q2. Поэтому при расчётах задаются значениями забойных давлений или дебитами рядов. Наиболее часто, исходя из технико-экономических соображений, обосновывают оптимальные значения забойных давлений в скважинах, т.к. значения забойных давлений ограничены давлением насыщения нефти газом. В наиболее общем виде формула интерференции рядов одновременно работающих скважин имеет следующий вид: 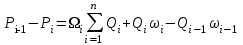 , (3.9) , (3.9)причём i = 1,2,3…n. Подставляя в это уравнение последовательно все значения i от 1 до n, получим систему алгебраических уравнений n-го ранга, из которой можно определить n неизвестных. Нумерация рядов при этом принята от внешних к внутренним рядам. Формулы (3.7) и (3.9) выведены при следующих упрощающих решение предпосылках. 1. Залежь считается однородной, но если она не однородна, то известен закон распределения неоднородных величин. 2.Вязкость нефти и воды считается постоянной как по залежи, так и по времен. 3. В одном и том же ряду одинаковые: расстояния между скважинами, дебиты скважин, забойные давления и радиусы скважин. 4. Расстояние от контура питания до первого ряда скважин больше половины расстояния между скважинами в ряду L>2Ϭ 5. Полосовая залежь предполагается неограниченной по длине или же принимают, что ее границы перпендикулярны рядам скважин. 3.1.1. Пример решения типовой задачи Задача 3.1. В полосообразной залежи совместно работают три ряда по 10 добывающих скважин в ряду. Определить суммарный дебит скважин каждого ряда, соотношение дебитов рядов и дебит, приходящийся на каждую скважину. (рис. 3.4). 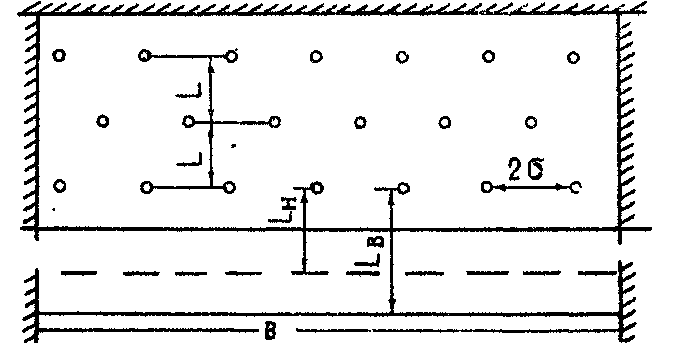 Рис. 3.4. Схема эксплуатации трех рядов скважин полосообразной залежи Ширина залежи B = 4км, расстояние между скважинами в ряду 2 = 400 м; радиус скважин rC = 0,1 м; расстояние между рядами L = 500 м; расстояние от внешнего контура нефтеносности до первого ряда LВ = 1000 м; расстояние от внутреннего контура нефтеносности до первого ряда Lн = 600 м; толщина пласта h = 10 м; коэффициент проницаемости пласта К = 0,5 мкм2; динамическая вязкость нефти Н = 3,0 мПа.с; динамическая вязкость воды В = 1,5 мПа.с; давление на контуре питания РК = 15 МПа; забойное давление в скважинах всех рядов одинаково и равно Рс = 9 МПа. Решение. Для определения суммарных дебитов рядов и скважин используют приведенный контур питания – условный контур (в общем случае не совпадающий с реальным контуром питания), где пластовое давление принимается равным давлению на реальном контуре питания. 1. Определяем приведённый контур питания: 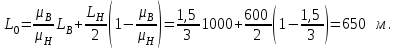 2. Для составления системы уравнений построим эквивалентную схему фильтрационных сопротивлений (рис. 3.5). 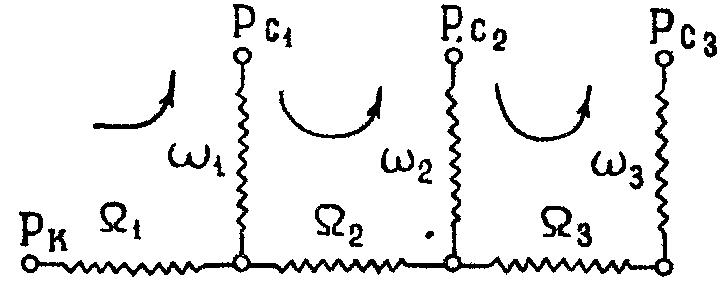 Рис. 3.5. Эквивалентная схема эксплуатации трех рядов скважин 3. Так как для написания уравнений используется второй закон Кирхгофа, выбираем направления обхода контуров, как это показано на рис. 3.5 Если направление потока жидкости совпадает с направлением обхода, то в уравнении ставим +, если не совпадает, то -. 4. Составляем систему из трёх уравнений:  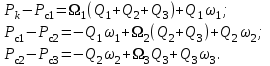 (3.10) (3.10)Ввиду равенства забойных давлений РС1 = РС2 = РС3 = РС система уравнений (3.10) несколько упрощается и записывается в виде  (3.11) (3.11)5. Рассчитываем внешние и внутренние сопротивления рядов скважин: 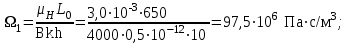  По условию задачи расстояния между рядами равны, поэтому Ω3= Ω2= 75.0 ∙ 106 Па ∙ с/м3 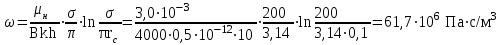 Подставляя численные значения гидродинамических сопротивлений в уравнения (3.11) и сократив в левой и правой части 106, получим 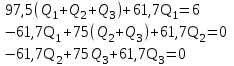 6. Полученную систему уравнений решаем методом последовательного исключения неизвестных снизу-вверх. Из третьего уравнения получим Q2 Q2=2,2Q3 Подставив его во второе уравнение, получим Q1 Q1=6,1Q3 Из первого уравнения рассчитаем Q3 Q3 =402,3 м3/сут. Рассчитаем Q2 и Q1 Q2=891,4 м3/сут Q1=2464,2 м3/сут Суммарный дебит трёх рядов составит: Qсум = Q1+Q2+Q3 = 3757,8 м3/сут. Соотношение дебитов рядов Q1 / Q2 = 2,8 Q2 / Q3 = 2,2 Q1 / Q3 = 6,1 Дебит одной скважины по рядам, м3/сут: 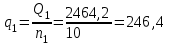 q2=89,1 q3=40,2 Вывод. Как видим из полученных результатов расчётов, при равенстве забойных давлений отборы жидкости по рядам скважин распределяются крайне неравномерно. При необходимости выравнивания отборов жидкости по рядам скважин можно изменить соотношения гидродинамических сопротивлений путём выбора расстояний между скважинами и рядами, а также увеличением забойных давлений в скважинах первых рядов. Задача для самостоятельного решения по вариантам Полосообразная залежь разрабатывается на жестководонапорном режиме. Контур питания представляет собой ряд водонагнетательных скважин. Три добывающих ряда по 10 скважин в ряду. Определить суммарный дебит скважин каждого ряда, соотношение дебитов рядов и дебит, приходящийся на каждую скважину. Для всех вариантов принять Pк=15 МПа, rс=0,1 м, h=10 м.
3.2. Круговая залежь. Гидродинамические расчеты по определению дебитов рядов скважин в случае круговой залежи проводятся по формулам, полученным также исходя из принципов электроаналогии. Дебит одной скважины, работающей в круговой батарее (рис. 3.16), определяется по формуле [9] 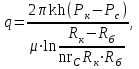 (3.16) (3.16)где k – коэффициент проницаемости пласта; h – толщина пласта, м; РК и РС – соответственно давление на контуре кругового пласта и в скважинах; - вязкость жидкости; RK и Rб – соответственно радиус контура питания и радиус батареи скважин; n – число скважин в батарее; rС – радиус скважин , причём  , где - половина расстояния между скважинами. (т.к. 2Ϭ=2πRб/n) , где - половина расстояния между скважинами. (т.к. 2Ϭ=2πRб/n)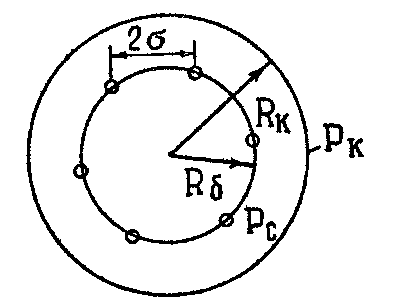 Рис. 3.6. Схема круговой залежи Формула (3.16) справедлива в случае фильтрации однородной жидкости в однородном пласте постоянной толщины. Давление во всех скважинах одинаково и расстояния между скважинами в круговой батарее равны. Принимая, что RK>>Rб, из (3.16) можно получить 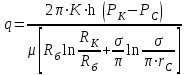 . (3.17) . (3.17)По аналогии с предыдущим случаем 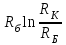 обозначают через RC, а обозначают через RC, а  - через Ri. - через Ri.Таким образом, RC является внешним, а Ri – внутренним сопротивлением скважины. Проведя некоторые преобразования, получим формулу для суммарного дебита всех скважин Q, работающих в круговой батарее, т.е. дебита ряда: 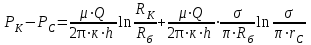 . (3.18) . (3.18)Внешние и внутренние сопротивления рядов скважин в этом случае рассчитываются по формулам 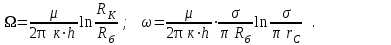 (3.19) (3.19)Общая схема составления системы уравнений (3.10) остается справедливой и для случая круговой залежи. Следует лишь помнить о том, что в случае круговой залежи внешние и внутренние сопротивления рядов изменяются. Залежь заливообразной формы можно схематизировать сектором, тогда в формулы Ω и ω вместо 2π надо подставлять угол сектора в радианах. 3.2.1. Пример решения типовой задачи по расчету дебитов рядов скважин в круговой залежи Задача 3.2. Определить суммарный отбор жидкости, дебиты скважин и забойные давления в круговой залежи при постоянстве дебитов скважин (рис. 3.6). Радиусы рядов, м: 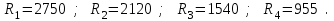 Радиус внешнего контура нефтеносности 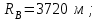 внутреннего внутреннего 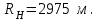 Количество скважин в рядах: n1=35 скв., n2=27 скв, n3=20 скв, n4=6 скв Расстояния между скважинами в рядах 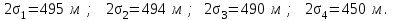 Средняя толщина пласта h = 12,4 м. Давление насыщения нефти газом Pнас=9,5 Мпа. Среднее значение коэффициента проницаемости пласта: к = 0,412 мкм2, вязкость нефти н = 3,0 мПа.с; вязкость воды в = 1,5 мПа.с; давление на контуре питания Рк = 17,5 МПа; радиус скважин rс = 0,15 м Все линейные размеры расчетной модели пласта определены при схематизации условий разработки залежи. 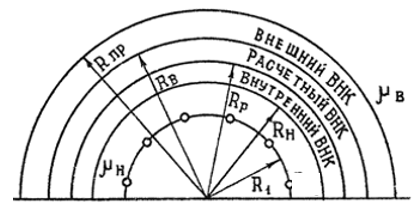 Рис.3.6. Схема расположения контуров нефтеносности в круговой залежи. Составляем эквивалентную электрическую схему (рис. 3.7). 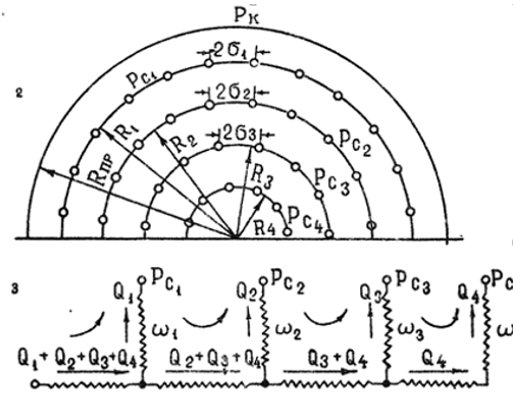 Рис. 3.7. Расчетная схема круговой залежи. 2. Рассчитываем приведенный контур питания по формуле [1] 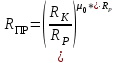 ( 3.20) ( 3.20)За Rк принимаем радиус внешнего контура нефтеносности Rв, 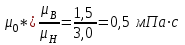 (3.21) (3.21)Rн - внутренний ВНК, Rв - внешний ВНК      Находим расчетный контур питания Rр 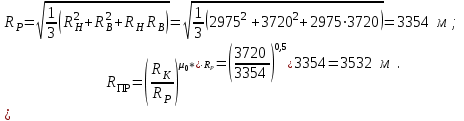 3. По эквивалентной электрической схеме, используя второй закон Кирхгофа, составляем систему уравнений, с учетом того, что дебит ряда Q=nq (3.22) 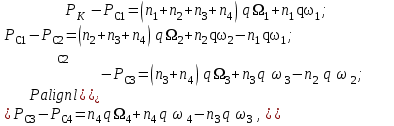 При равенстве дебитов скважин максимальное давление будет в скважинах первого ряда. По мере удаления рядов от контура залежи давление уменьшается и скважины внутреннего ряда работают при минимальном забойном давлении. Поэтому необходимо обосновать минимальное допустимое значение забойного давления из геолого-технических условий разработки месторождения. Часто минимальное значение давления в скважинах принимают равным давлению насыщения нефти газом. Принимаем давление в скважинах четвертого ряда равным давлению насыщения:  4. Рассчитываем внешние и внутренние сопротивления рядов скважин: 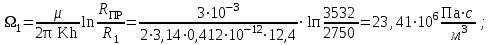 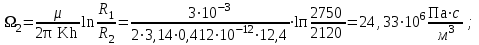 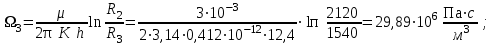 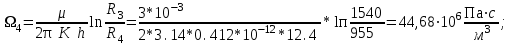 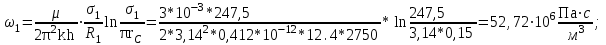 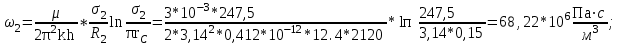 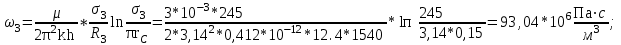 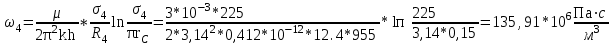 Перепишем уравнение (3.22) с учетом числовых значений давлений, количества скважин и сопротивлений: (3.23) Перепишем уравнение (3.22) с учетом числовых значений давлений, количества скважин и сопротивлений: (3.23)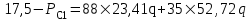 ; ;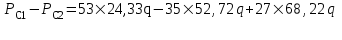 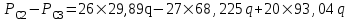 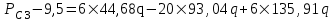 или:  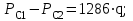 (3.24) (3.24)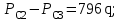 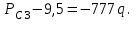 (Pc4 = 9.5 Мпа - давление насыщения) Последовательно исключая неизвестные забойные давления снизу-вверх, получим дебит одной скважины q=1,72∙10-3 м3/с=148,5 м3/сут Дебиты рядов скважин: м3/сут  Q1=n1∙q=5197,3 ∙ Q2=4009,4 Q3=2969,9 ∙ Q4=891,0 Суммарный суточный отбор жидкости из залежи составит: Qсум сут=13067,5 м3/сут Годовой отбор жидкости из залежи: 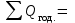 365 ∙ Qсум сут=365∙ 13067,5 = 4,77 млн.м3/год 365 ∙ Qсум сут=365∙ 13067,5 = 4,77 млн.м3/годПо формулам (3.24) можно определить значения давлений в скважинах в добывающих рядах: Pc1=12,9 Мпа Pc2=10,7 Мпа Pс3=9,4 МПа Таким образом, при равенстве дебитов скважин максимальное давление устанавливается в скважинах первого ряда. По мере нарастания номера ряда забойные давления уменьшаются. 3.3. Задача для самостоятельного решения 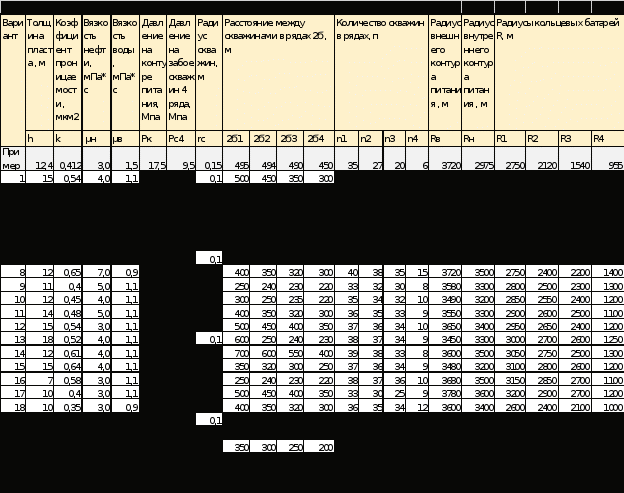 |
