кенренре. Романюк_Г_Д_ЭЭТбд-2201а(3). 3 по учебному курсу Высшая математика

• Название: 3 по учебному курсу Высшая математика
• Анкор: кенренре
• Дата: 30.04.2023
• Размер: 0.98 Mb.
• Имя файла: Романюк_Г_Д_ЭЭТбд-2201а(3).doc
• Тип: Документы; #1098913

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное бюджетное образовательное учреждение высшего образования

«Тольяттинский государственный университет»
СДО Росдистант

(наименование института полностью)

Тольяттинский государственый университет

(Наименование учебного структурного подразделения)

13.03.02 Электроэнергетика и электротехника

(код и наименование направления подготовки / специальности)

Электроснабжение

(направленность (профиль) / специализация)

Практическое задание №3
по учебному курсу «Высшая математика. Элементы высшей алгебры и геометрии»

^{(наименование учебного курса)}
Вариант 5

Обучающегося	Романюк Глеб Дмитриевич
	(И.О. Фамилия)
Группа	ЭЭТбд-2201а
Преподаватель	Крылова Светлана Александровна
	(И.О. Фамилия)

Тольятти 2023

Раздел № 3. Аналитическая геометрия

Задача 1.5.

Даны координаты вершин треугольника АВС. Составить уравнения сторон треугольника. Составить уравнения медианы, высоты и биссектрисы угла А, найти их длины. Составить уравнения прямых, проходящих через вершины треугольника и параллельных его сторонам.

A(0; 4), B(-5; -1), C(2; 2).

Решение.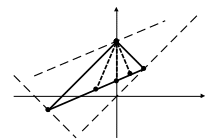

у

А

С

М D Н

х

В


АН – высота, АМ – медиана, АD – биссектриса.

1) Уравнения сторон треугольника.

Уравнение стороны АВ:

;

;

;

;

.

Уравнение стороны АС:

;

;



;

.

Уравнение стороны ВС:

;

;

;

;

.
2) Уравнение медианы угла А и длина медианы.

Координаты точки М, являющейся серединой стороны ВС:

;

.

Уравнение медианы АМ:

;

;

;

;

;

.

Длина медианы АМ:

ед.
3) Уравнение высоты угла А и длина высоты.

Угловой коэффициент стороны ВС:

.

Высота АН перпендикулярна стороне ВС. Найдём угловой коэффициент высоты АН из условия перпендикулярности прямых:

;

.

Уравнение высоты угла А:

;

;

.

Векторы , и :

;

;

.

Площадь треугольника АВС:

ед .

Длина стороны ВС:

ед.

Площадь треугольника равна половине произведения стороны на высоту, проведённую к этой стороне:

.

Тогда длина высоты АН равна:

ед.
4) Уравнение биссектрисы угла А и длина биссектрисы.

Длина сторон АВ и АС:

;

.

Точка D биссектрисы АD лежит на стороне ВС. Из равенства углов ВАD и САD следует:

;

;

;

;

;

;

;

.

Точка D лежит на стороне ВС, то есть её координаты удовлетворяют уравнению стороны ВС:

;

.

Точка D имеет координаты .

Уравнение биссектрисы АD:

;

;

;

;

.

Длина биссектрисы АD:

ед.
5) Уравнения прямых, проходящих через вершины треугольника и параллельных его сторонам.

Для прямой, проходящей через вершину А параллельно стороне ВС, направляющим является вектор . Уравнение прямой:

;

;

;

.

Для прямой, проходящей через вершину В параллельно стороне АС, направляющим является вектор . Уравнение прямой:

;

;

;

.

Для прямой, проходящей через вершину С параллельно стороне АВ, направляющим является вектор . Уравнение прямой:

;

;

;

.