Автокорреляция. Автокорреляция_26.04.2022. Автокорреляция Наблюдаемые значения случайного члена коррелированны друг с другом. (Нарушение одного из условий гауса маркова) Автокорреляция первого порядка
 Скачать 153.83 Kb. Скачать 153.83 Kb.
|
|
Автокорреляция - Наблюдаемые значения случайного члена коррелированны друг с другом. (Нарушение одного из условий гауса маркова) 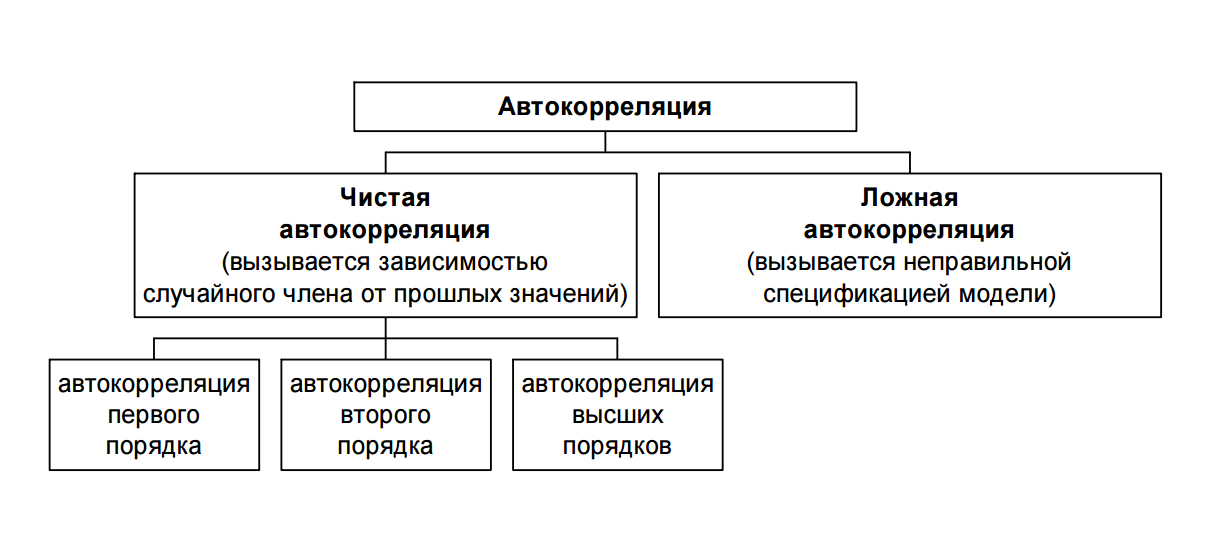 Автокорреляция первого порядка εt = ρε −1 +ut −1< ρ < 1 В более высоких порядках протяженность зависимости во времени больше 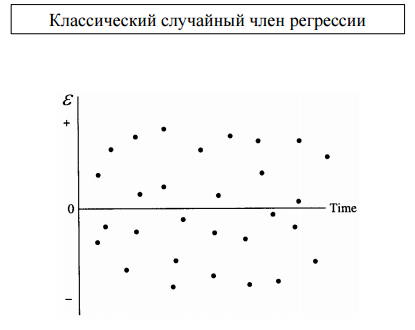  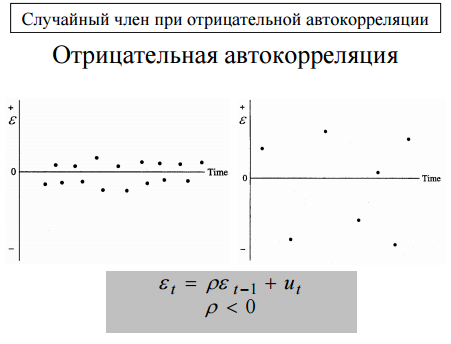 Последствия автокорреляции 1. Истинная автокорреляция не приводит к смещению оценок коэффициентов регрессии. 2. Положительная автокорреляция (наиболее важный для экономики случай) приводит к увеличению дисперсии оценки коэффициентов. (более сложные случаи, в том числе лаговые переменные, рассматриваются далее). 3. Автокорреляция вызывает занижение оценок стандартных ошибок коэффициентов. Обнаружение автокорреляции. Тест Дарбина-Уотсона Статистика Дарбина-Уотсона предназначена для обнаружения автокорреляции первого порядка. Она основана на изучении остатков уравнения регрессии. 1.Статистика Дарбина-Уотсона не предназначена для обнаружение других видов автокорреляции (второго порядка, сезонной автокорреляции) и не обнаруживает ее. 2. В модели регрессии должно быть использовано уравнение с постоянным членом. Для регрессии без постоянного члена применение статистики Дарбина- Уотсона некорректно. 3. Лаговая зависимая переменная не используется в качестве независимой. 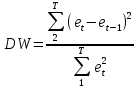 По хорошему надо использовать критические значения статистики, причем в данном случае два критических значения нижнее и верхнее. Практическое использование теста Дарбина-Уотсона. H 0 : ρˆ = 0 (нулевая гипотеза отсутствия положительной автокорреляции) H A : ρˆ > 0 (альтернативная гипотеза наличия положительной автокорреляции). Решающее правило: Если d < d L , то гипотеза H 0 отвергается. Если d > dU , то гипотеза H 0 не отвергается. Если d L ≤ d ≤ dU , то ситуация остается неопределенной («темная зона») H0 : ρˆ = 0 (нулевая гипотеза отсутствия отрицательной автокорреляции) : ρ ˆ < 0 HA (альтернативная гипотеза наличия отрицательной автокорреляции). Решающее правило: Если L d > 4 − d , то гипотеза H0 отвергается. Если U d < 4 − d , то гипотеза H0 не отвергается. Если U L 4 − d ≤ d ≤ 4 − d , то ситуация остается неопределенной («темная зона») «Правило большого пальца» для DW коэффицента DW = 0 положительная АК 1ого порядка DW = 4 отрицательная АК 1ого порядка DW = 2 Борьба: использование устойчивых оценок стд.ош. в форме Ньюи-Веста |
