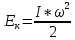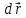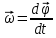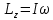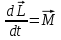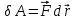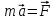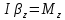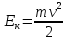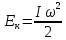Билет 22. Билет 22 Кинетическая энергия твёрдого тела, вращающегося вокруг неподвижной оси
 Скачать 34.87 Kb.
|
|
Билет 22 Кинетическая энергия твёрдого тела, вращающегося вокруг неподвижной оси Р 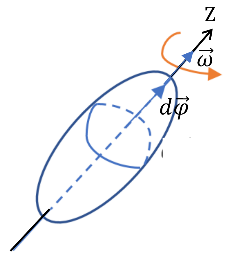 ассмотрим ААТ (абсолютно твердое тело), вращающееся с угловой скоростью 𝜔⃗ вокруг неподвижной оси, совпадающей с осью 𝑍.Пусть за время 𝑑𝑡 тело поворачивается на угол 𝑑𝜑⃗: 𝑑𝜑⃗ = 𝑑𝜑 ∙ 𝑘⃗, 𝑘⃗ − единичный вектор оси Z. Сосчитаем работу, совершённую силами, действующими на АТТ:  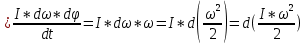 По теореме о кинетической энергии работа всех сил, действующих на тело, равна приращению его кинетической энергии:
 Получаем формулу кинетической энергии твердого тела, вращающегося вокруг неподвижной оси. Это выражение напоминает выражение для кинетической энергии МТ (материальной точки), только вместо массы фигурирует момент инерции, а вместо линейной скорости – угловая: 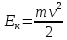 .Аналогии между движением МТ и вращением АТТ вокруг неподвижной оси
Динамика плоского движения АТТ При плоском движение АТТ его центр масс (𝐶) движется в определённой плоскости, неподвижной в системе отсчёта, а вектор его угловой скорости 𝜔⃗ всё время остаётся перпендикулярным этой плоскости. Т.е. в системе центра масс АТТ тело просто вращается относительно неподвижной оси, проходящей через точку 𝐶 и перпендикулярной плоскости движения. 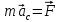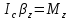Из этого следует, что плоское движение АТТ можно описывать двумя уравнениями:  - уравнение движения центра масс системы (поступательное движение АТТ как целого) - уравнение динамики АТТ, вращающегося вокруг неподвижной оси (вращение АТТ), где 𝑀𝑧 суммарный момент всех внешних сил относительно оси, проходящей через центр масс (𝐶).Кинетическая энергия АТТ при плоском движении тоже складывается из энергии движения центра масс (поступательного движения) и энергии вращения вокруг неподвижной оси, проходящей через точку 𝐶:  |
