Биопотенциалы. Тема_4_2_семестр_Биопотенциалы. Биофизика тема 4 Биоэлектрические потенциалы
 Скачать 116.51 Kb. Скачать 116.51 Kb.
|
|
БИОФИЗИКА Тема_4 Биоэлектрические потенциалы. В живых организмах происходят разнообразные электрические процессы. Функционирование живых тканей сопровождается электрическими явлениями. Генерация и распространение электрических потенциалов - важнейшее физическое явление в живых клетках и тканях. Биоэлектрический потенциал - разность потенциалов между двумя точками живой ткани, определяющая ее биоэлектрическую активность. Биопотенциал имеет мембранную природу. Ионные потоки в мембране Сквозь мембрану проходят потоки ионов, для которых справедливо уравнение Нернста-Планка: Эйнштейн показал, что подвижность ионов Um выражается через коэффициент диффузии D и абсолютную температуру Т: Um = D/(RT), тогда уравнение Нернста-Планка принимает вид: В первом приближении можно считать, что поле внутри мембраны однородно. В этом случае dp/dx = φм/l, где L - толщина мембраны, а φм - разность потенциалов между стенками мембраны. Теперь уравнение Нернста-Планка будет иметь вид:  Для упрощения записи введем величину ψ, которую называют безразмерным потенциалом:  Тогда уравнение Нернста - Планка будет иметь вид:  Решив это уравнение методом разделения переменных, получим выражение для потока ионов через мембрану:  Это уравнение устанавливает количественную связь между плотностью потока какого-либо иона и следующими величинами, характеризующими мембрану: безразмерный потенциал ψ, проницаемость мембраны для данного иона Р, концентрация иона в водной среде по обе стороны мембраны (сi и с0). Проанализировав частные случаи полученного уравнения, можно сделать вывод, что: 1. Пусть ψ=0, что означает либо Z=0, (нейтральные частицы в поле есть, но переносить нечего), либо отсутствие электрического поля в мембране (φм=0, и даже при наличии ионов ничего переносится не будет), или и то и другое тогда уравнение будет иметь вид:  При этом вся диффузия будет обусловлена нейтральными молекулами. 2) Если сi = с0=с - одинаковая концентрация ионов по разные стороны от мембраны при наличии электрического поля, то Это соответствует электропроводности в электролите. 3. Р=0, Мембрана непроницаема для частиц, плотность потока равна нулю. Потенциал покоя. В нормально функционирующей клетке поддерживается наиболее благоприятный состав ионов. Концентрация каких- либо определенных ионов различна по разные стороны мембраны. Это приводит к появлению разности потенциалов в нормально функционирующей клетке Потенциал покоя - разность потенциалов между цитоплазмой и окружающей средой в нормально функционирующей клетке. Получим уравнение, позволяющее вычислить потенциал покоя. 0 Через мембрану проходят потоки разных ионов. Основной вклад в суммарный поток, а, следовательно, в создание и поддержание потенциала покоя вносят ионы Na+, К+, Сl-. Суммарная плотность потока этих ионов с учетом их знаков равна^ 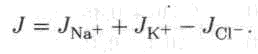 В стационарном состоянии (когда параметры системы не изменяются) суммарная плотность потока равна нулю, то есть число различных ионов, проходящих в единицу времени через мембрану внутрь клетки, равно числу ионов, выходящих из клетки через мембрану: J= 0. Для потока различных ионов электрический мембранный потенциал равен: 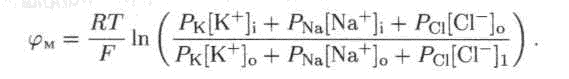 Здесь квадратными скобками [ ]i, и [ ]o обозначены концентрации ионов, соответственно, внутри и вне клетки. Полученное выражение называется уравнением Гольдмана-Ходжкина-Катца, оно отражает состояние системы в том случае, когда через мембрану непрерывно идут встречные потоки ионов. Мембранный потенциал (потенциал покоя) зависит от различия концентрации ионов и от проницаемости. В качестве примера использования уравнения Гольдмана-Ходжкина-Катца рассчитаем потенциал покоя для гигантского аксона кальмара. Значения концентраций приведены ниже.  В состоянии покоя при физиологических условиях соотношение коэффициентов проницаемости равно: PK:PNa:PCl=1:0,04:0,045 Проницаемость мембраны для ионов калия самая высокая. Диффузия калия и хлора идет в обе стороны. Натрий идет через мембрану за счет простой диффузии лишь в одну сторону -- снаружи вовнутрь. Однако АТФаза интенсивно выводит ионы натрия из клетки, а калий -- в клетку. Следовательно, основной вклад в потенциал покоя вносят только ионы К+ и Сl-. Из уравненияГольдмана-Ходжкина-Катца можно получить уравнение для равновесного состояния. При этом следует пренебречь проницаемостями всех ионов, кроме ионов одного вида. Тогда имеем уравнение Нернста: Эту разность потенциалов называют равновесным мембранным потенциалом. |
