Доклад на тему
 Скачать 283.49 Kb.
|
|
МБОУ Первомайская СОШ Доклад на тему: «Использование развивающих заданий на уроках естественно – математического цикла и во внеурочное время, как важнейшее направление работы с одаренными детьми» » Учитель математики Кириченко Е.С. 2021 «Использование развивающих заданий на уроках естественно – математического цикла и во внеурочное время, как важнейшее направление работы с одаренными детьми» Перспективным и важным направлением в работе с детьми, имеющие склонности к математике, является развитие у них логического мышления, которое подразумевает формирование приёмов мыслительной деятельности, а также понимать и прослеживать причинно-следственные связи явлений, выстраивать простейшие умозаключения. Обязательным условием развития логического мышления у интеллектуально одарённых детей, на мой взгляд, является формирование приёмов умственных действий: сравнения, обобщения, анализа, синтеза, аналогии, систематизация, абстрагирования Работа с одарёнными детьми проводится мною по следующим основным направлениям: Использование логических заданий на уроках математики. Подготовка и проведение олимпиад разного уровня. Проведение математических соревнований. Исследовательская работа. Кружковая работа. Проведение математических соревнований. В процессе изучения математики немаловажным является принцип соревнования. Интерес учащихся к изучению предмета прекрасно «подогревается» различного рода конкурсами, викторинами, математическими боями. Здесь стараюсь и рассмотреть вопросы, на которые не остается места в рамках обычной школьной программы. Акцент делаю на задачах занимательного характера и необычного содержания. Ниже приводится список задач, которые можно предложить для учащихся 5-7 классов. Выразите числа 5, 26, 30 и 55, используя четыре цифры 5, знаки арифметических действий и скобки. Существуют ли 4 различных натуральных числа таких, что сумма любых трех из них – простое число? После семи стирок длина, ширина и высота куска мыла уменьшились вдвое. На сколько стирок хватит оставшегося куска? Малыш и Карлсон пилили дрова. Они сделали 22 распила и получили 32 полена. Сколько бревен было у Малыша и Карлсона? После того, как Катя съела половину персиков из банки, уровень компота понизился на одну треть. На какую часть (от установившегося нового уровня) понизится уровень компота, если съесть половину оставшихся персиков? В ряд выписаны пять чисел, имеющих положительную сумму. Может ли быть так, что сумма любых трех идущих подряд чисел отрицательна. На доску выписаны 6 чисел: 1,2,3,4,5,6. Разрешается к любым двум прибавить по 1. Можно ли, проделав эту операцию несколько раз, сделать эти числа равными. Учитель отметил на прямой несколько точек. Затем Вова между каждыми двумя соседними точками поставил еще по одной точке. Затем то же самое сделали Катя и Маша. После этого Петя посчитал все отмеченные точки и сказал, что их 122. Учитель, не глядя на доску, заявил, что Петя ошибается. Почему он так решил? Три красных и три белых шара выложены в ряд. Доказать, что можно поменять местами два шара так, чтобы шары одного цвета лежали рядом. Сколькими способами из пяти квадратов можно сложить прямоугольник? Квадраты при этом можно брать каких угодно размеров. Та же задача для шести квадратов. Математические олимпиады . Математические олимпиады являются важной составной частью математического образования. Они позволяют выявить и развить такие качества учащегося, которые не всегда проявляются в повседневном учебном процессе. Не секрет, что очень часто отлично усваивающие школьный материал учащиеся теряются при решении олимпиадных задач и не добиваются в олимпиадах высоких результатов. Это связано с тем, что успешное выступление в олимпиадах требует специфических качеств и особых способностей, которые, естественно, тоже следует развивать. С этой целью помимо основного цикла олимпиад я способствую участию детей в олимпиадах различного рода и уровня. Среди них, в частности, Международная олимпиада «Эрудит», Международная олимпиада математическая олимпиада «Кенгуру», Всероссийский дистанционный конкурс по математике «Олимпис», Всероссийский математический конкурс «Ребус». Дети с огромным желанием участвуют в олимпиадах! Исследовательские задачи. На мой взгляд, задачи такого сорта имеют две характерные черты. Во-первых, эти задачи многовариантны. Они как бы состоят из большого количеств различных по сложности задач – от совсем простых частных случаев, до трудноразрешимых (а, возможно, и неразрешимых) проблем. Причем в процессе решения одних задач часто возникают другие, порой гораздо более интересные. Во-вторых, в своей формулировке исследовательская задача не предполагает известным ответ на поставленный в ней вопрос. Более того, по ходу решения такой задачи часто удается ответить вовсе не на тот вопрос, который в этой задаче первоначально ставился. То есть задача видоизменяется в процессе ее решения. Вообще-то любая хорошая задача содержит какие-то элементы исследовательской. П  оговорим теперь о задаче 10. Эту задачу с увлечением решали как пятиклассники, так и десятиклассники. Попробуйте и вы ее решить. Но сначала попытайтесь угадать, сколькими все-таки способами можно из пяти квадратов сложить прямоугольник. С первого взгляда кажется, что таких способов совсем немного. Однако потом выясняется, что среди различных конструкций встречаются весьма забавные. Например, такая, как на этом рисунке. Короче, всего у нас получилось 15 или 16 вариантов. Но вначале мы исследовали данную задачу для 3 квадратов (там всего два варианта) и для четырех квадратов. До шести квадратов так никто и не добрался.При решении задачи о пяти квадратах мы не ограничивались чисто описательной работой. Была установлена связь этой задачи с теорией графов. А именно, каждой конструкции сопоставлялся некий граф, получаемый так: вершины графа – квадраты. Если квадраты имеют общий участок границы, то соответствующие вершины соединяются ребрами. Например, для приведенной выше конструкции граф выглядит так. 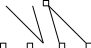 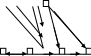 Выяснилось, что разным способам могут соответствовать одинаковые графы. Таким образом, глядя на граф, мы не сможем понять, какая конструкция породила этот граф. Однако на этом месте возникают разные любопытные вопросы, и не только для случая пяти квадратов. Например, верно ли, что каждый связный граф описывает некоторый способ построения прямоугольника из квадратов? Много ли различных способов порождают один и тот же граф? Как изменится ситуация, если вместо обычного рассмотреть ориентированный граф, в котором стрелочка направлена от большего квадрата к меньшему?При исследовании задачи о пяти квадратах изучался еще один вопрос: можно ли один и тот же прямоугольник различными способами сложить из пяти, шести или большего количества квадратов. Ответ на этот вопрос утвердительный, если разрешить перестановки внутри одной и той же конструкции, как это показано на рисунке: О  днако вопрос интересно поставить немного по-другому: можно ли из двух разных наборов квадратов сложить одинаковые прямоугольники? И если да, то при каком минимальном числе квадратов в таких наборах это можно сделать? Можно также потребовать, чтобы все квадраты в наборе были различными по размерам. В этом случае мы попадаем в ситуацию, описанную в известной книге И. М. Яглома «Как разрезать квадрат?» Решение некоторых задач из общего списка. 4. . Число бревен + число распилов = число поленьев 6. Да. Например, 2, 2, –5, 2, 2. 7. Сумма написанных чисел нечетна. После прибавления двух единиц она останется нечетной, а потому все шесть чисел нельзя сделать равными. 8. Если учитель поставил четное число точек, то Вова поставил их нечетное число, а все остальные дети – четное. Если же учитель поставил нечетное число точек, то все дети поставили их четное число. В любом случае сумма нечетна и не может равняться 122. 9. При решении этой задачи важно не упустить ни одного варианта взаимного расположения шаров. Первый (самый левый) шар можно считать белым. Тогда возможны 4 варианта расположения трех первых шаров: 1) БББ; 2) ББК; 3) БКБ; 4) БКК. В первом случае можно ничего не менять (или поменять местами два шара одного цвета). Во втором случае шар №3 меняем местами с третьим белым шаром. В третьем случае то же самое делаем с шаром №2, а в четвертом аналогично поступаем с шаром №1. За время работы на уроках учителя стараются применять различные педагогические технологии, но, проработав в школе некоторое время, стала замечать, что развивающие цели практически не меняются( развивать память, внимание, мышление.), а после многолетних наблюдений за учениками, я стала больше убеждаться, что обучение ребенка без его развития не может быть успешным. И зачастую слыша от детей фразы: « Включи логику!», « Думай логически!» пришла к выводу, что необходимо включать в уроки, а так же и во внеурочную деятельность развивающие задания. Эти задания помогают удерживать интерес к математике, что очень необходимо в современных условиях школьного обучения, а также важно направить одарённого ребёнка не на получение определённого объёма знаний, а на творческую его переработку, воспитать способность мыслить. Следует признать нецелесообразным в условиях школы выделение таких учащихся в особые группы для обучения по всем предметам. Одаренные дети должны обучаться в классах вместе с другими детьми. Это позволит создать условия для дальнейшей социальной адаптации одаренных детей и одновременно для выявления скрытой до определенного времени одаренности, для максимально возможного развития всех учащихся, для выполнения ими различного рода творческих заданий. Рассмотрим простейшую задачу, предлагаемую для решения детям 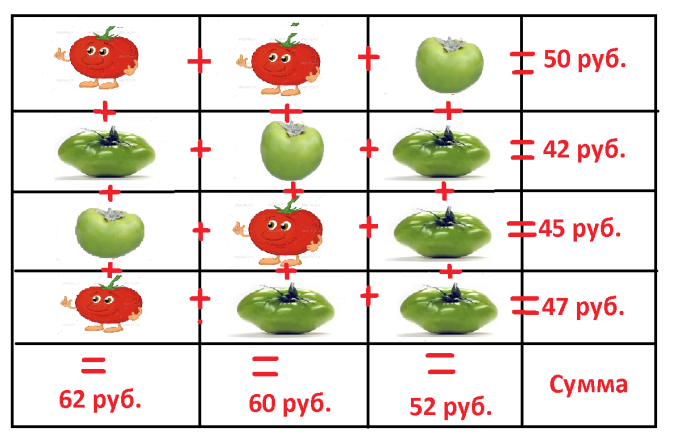 На рисунке показаны цены томатов. Какие томаты дороже: красные или зелёные? На сколько? Эту задачу я предлагала для решения в 5 и 9 классах. Оба класса справились с решением. Но сравнивая время, за которые оба класса справились с заданием я испытала недоумение: на решение этой задачи 9 классу понадобилось в среднем 25 минут, а вот 5 классу всего 10 минут. В чем же дело? Оказалось, что 9 класс решал задачу с помощью составления системы уравнений. А 5 класс рассуждал логически. Сравнив 1 и 3 строчку, они нашли разницу и определили, что красный томат на 5 рублей дороже зелёного. Стоит отметить, что это олимпиадная задача для начальной школы. Что это значит рассуждать логически? Это тема интересовала мир давно. Давайте вспомним, что такое универсальные учебные действия? Универсальные учебные действия (УУД)-это умение человека учиться, т.е. способность к самосовершенствованию через усвоение нового социального опыта. И еще раз вернемся к научному определению логики. Логика в переводе с древне-греческого – это «наука о правильном мышлении», « искусство рассуждать». И именно в развивающих задачах требуется применение этого качества. Развивающее обучение начинается еще в детском саду. Здесь очень важна преемственность. Сериация — построение упорядоченных возрастающих или убывающих рядов. Классический пример сериации: матрешки, пирамидки, вкладные мисочки и т. д. Сериации можно организовать по размеру: по длине, по высоте, по ширине — если предметы одного типа (куклы, палочки, ленты, камешки и т. д.) и просто «по величине» (с указанием того, что считать «величиной») — если предметы разного типа (рассадить игрушки по росту). Сериации могут быть организованы по цвету: по степени интенсивности окраски.    Самое простое задание с которым дети сталкиваются еще в детском саду и отработка, которого продолжается уже в школе –это восстановление недостающих элементов по картинкам. Далее задание усложняем. Эти задания встречаются и в информатике. Найдите следующее число: 1, 4, 9, 16, 25 .... В задании следует, найдя закономерность, учащимся предлагается выстроить логическую цепочку. Следующим шагом предлагается задание, в котором вариантов решения может быть несколько. Выявите закономерность и укажите следующие два числа. 9, 3, 12, 6, 15, 9, ..., ... Казалось бы эти упражнения абсолютно не найдут применения в старших классах. Но не тут то было. В 9 классе по алгебре есть тема арифметическая и геометрическая прогрессия, при решении которой данные навыки будут абсолютно не лишними. Подобные задания мы можем увидеть и ОГЭ. Дана арифметическая прогрессия: 33; 25; 17; … Найдите первый отрицательный член этой прогрессии. Следующим этапом в развитии универсальных учебных действий логического типа является анализ и синтез. Два действия, которые существуют неразрывно друг от друга.
У Маши есть 15 конфет, вместе у Маши и Лены 20 конфет. Сколько конфет у Лены? 1) 20 - 15 = 5 ( решение, основанное на синтезе); 2) x + 15 = 20 ( решение, основанное на анализе). В вариантах ОГЭ часто встречаются задачи такого плана. Акции предприятия распределены между государством и частными лицами в отношении 3:5. Общая прибыль предприятия после уплаты налогов за год составила 32 млн. р. Какая сумма из этой прибыли должна пойти на выплату частным акционерам? Это задача, которую можно решать двумя способами. Наши дети привыкли к решению, основанному на анализе. Поэтому часто можно услышать возмущение, что сложная задача находится в первой части. Наряду с отработкой навыка анализа и синтеза идет работа над умением классифицировать. На раздаточном материале написаны слова: Круг, треугольник, квадрат, пирамида, куб, арбуз, мяч. Учитель просит распределить учащихся данные предметы на две группы( вариантов классификации может быть несколько). Виды упражнений на классификацию. Расположите в порядке убывания числа 1,4302; 1,43; 1,437. Из каких чисел можно составить верную пропорцию? А. 3, 4, 8, 10; Б. 8, 10, 12, 15; В. 2, 3, 4, 5; Г. 3, 6, 9, 21. 4)Укажите НЕВЕРНОЕ утверждение: А. В любом треугольнике либо все углы острые; либо два угла острые, а третий угол - тупой или прямой; Б. Внешний угол треугольника равен сумме двух углов, не смежных с ним; В. В тупоугольном треугольнике сумма углов больше 180 градусов; Г. Сумма углов треугольника равна 180 градусам. 5) Соберите в левой части уравнения -4х+3,6 = 3х - 2,1 все слагаемые, содержащие неизвестное, а в правой - не содержащие неизвестное. Поскольку конечны результатом нашей работы является экзамен. То вся работа направлена на его успешную сдачу. Задания из ОГЭ. На рисунке изображены графики функций вида y = ax2 + bx + c. Для каждого графика укажите соответствующее ему значения коэффициента a и с. 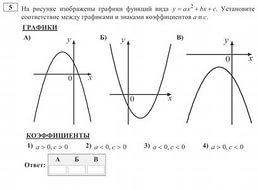 И наконец, как наивысшая способность классифицировать – это умение составлять опорные схемы или конспекты. Зздесь нужно анализировать, классифицировать по определенным признакам и синтезировать в конечный результат. Но выполняя любое задание, учащиеся прилагают определенные усилия и, как мы иногда говорим, пропускают знания через себя, свои эмоции и чувства. Стоит вспомнить о том, что в 10 классе геометрия переходит из плоскости в пространство. У многих это вызывает определенные затруднения при решении задач. Но это можно предотвратить, если начать работу по данной теме еще в 5 классе. Салфетки и пространственное воображение. Вы последовательно кладете 8 одинаковых салфеток квадратной формы на стол, одну на другую. Одна салфетка, помеченная буквой А, находится на самом верху. Другие видны только частично, и некоторая часть их скрыта. В каком порядке салфетки были положены на стол? 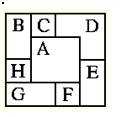 Если выписать порядок укладки салфеток (начиная с первой - самой нижней), то какая по счету будет салфетка В? (a) 1; (b) 2; (c) 3; (d) 4; (e) 5; (f) 6; (j) 7; 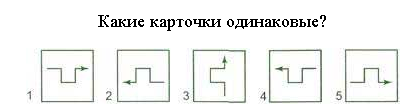 Среди этих пяти карточек есть три одинаковых. Какие? 1)Возьмите 12 спичек. Составьте из них квадраты. У кого получилось больше всех квадратов? (3) 2)Квадраты можно составлять так, чтобы одна и та же спичка была стороной двух смежных квадратов. (5) 3)А какие две спички нужно убрать , чтобы получилось два неравных квадрата? 4) А теперь в полученной фигуре переложить три спички так, чтобы образовалось три равных квадрата? 5) Из двенадцати спичек составить 8 равных квадратов. (куб) Обязательно необходимо применять материал олимпиадных заданий, заданий игры- конкурса « Кенгуру», заданий на смекалку в работе и во внеурочное время. Проводить предметные недели, конференции, интеллектуальные конкурсы, марафоны различного уровня, элективные курсы. Одним из видов развивающего обучения считаю написания сочинения на заданную тему. Во время выполнения этой работы учащиеся учатся анализировать, синтезировать, видеть реальное применение математики. Предлагаю вашему вниманию отрывок из сочинения ученицы 9 класса на тему « Что такое математика». Сказочный город Сейчас я расскажу историю, которая произошла в городе с названием Математика. Математика – это большой и красивый город. В этом городе живут разные математические предметы, знаки, фигуры, числа и многие другие жители. Делится он на два района : Алгебра и Геометрия. Вот однажды, в Алгебре случилось несчастье, в Математике очень редко такое случается, так как все жители очень пунктуальны и постоянны. Самая интеллигентная дама – Система Координат потеряла своего друга Начало Координат, а по-простому, она называла его Нулем. Подойдя к Линейке, она спросила о Нуле, но Линейка ничего не знала о нем. Решила она сама искать своего пропавшего друга Начало Координат. Часто мы с детьми пишем сказки. Выбирается раздел, из которого предлагается выбрать самое важное и написать творческую работу. Главная задача учителя - помочь одаренному ребенку вовремя проявить и развить свой талант. Психологические особенности одаренных детей: Есть одаренные ребята, в которых удачно сочетаются высокий интеллект, творчество и скромность, доброта, чуткость, внимательное отношение к людям. У одаренных ребят есть еще один стимул - побеждать. Хотя цена этих побед - долгая и трудная работа над собой. И здесь незаменима помощь учителей. «Технические достижения не стоят ровным счетом ничего, если педагоги не в состоянии их использовать. Чудеса творят не компьютеры, а учителя!» - отмечает КрейгБарретт, и с этим невозможно не согласиться. Обучение талантливого ребенка и выработка у него умения самостоятельно усваивать сложный материал – это тот первый шаг, который должен проделать педагог со своим подопечным, чтобы привить ребенку вкус к серьезной, включающей в себя элементы творческого подхода работе, которая будет сопутствовать данному ребенку в жизни. Кроме того, вводя талантливого ребенка в предмет исследования, приобщая его к науке, необходимо ставить конкретную задачу, а именно, развитие самостоятельности в принятии решений по научным вопросам и проблемам, а также придумывание ребенком своим, качественно новых идей. Немаловажную роль в этом играет реакция взрослых, умение учителя создать максимально благоприятные условия для всестороннего развития ребёнка, стимулировать творческую деятельность одарённых детей, что, как показывает опыт, возможно сделать на уроках. Задача учителя состоит в том, чтобы создать условия практического овладения языком доступным для каждого учащегося, выбрать такие методы обучения, которые позволили бы каждому ученику проявить свою активность и творчество. В заключение хотелось бы отметить, что работа педагога с одаренными детьми — это сложный и никогда не прекращающийся процесс. Он требует от учителя личностного роста, хороших, постоянно обновляемых знаний в области психологии одаренных и их обучения, а также тесного сотрудничества с психологами, другими учителями, администрацией и обязательно с родителями. Он требует постоянного роста мастерства педагогической гибкости, умения отказаться оттого, что еще сегодня казалось творческой находкой и сильной стороной. Об этом очень точно высказался Сократ: «Учитель, подготовь себе ученика, у которого сам сможешь учиться». Список литературы: 1. Андреев В.И., «Диалектика воспитания и самовоспитания творческой личности. Основы педагогики творчества», Казань, 2007. 2. Лейтес Н.С. Возрастная одаренность и индивидуальные различия: избранные труды. – М.: Издательство Московского психолого-социального института; Воронеж: Издательство НПО «МОДЭК», 2003. 3. Опыт работы с одаренными детьми в современной России. Сборник материалов Всероссийской научно-практической конференции / Науч. ред. Н.Ю. Синягина, Н.В. Зайцева. – М.: Арманов-центр, 2010. 4. Опыт работы с одаренными детьми в современной России: материалы Всероссийской научно-практической конференции. Москва, 6-8 февраля 2003 года/ Научный редактор Л.П. Дуганова |