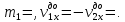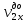Закон сохранения энергии. Лаболаторная работа 2. Эксперимент Абсолютно упругий удар
 Скачать 23.15 Kb. Скачать 23.15 Kb.
|
|
Эксперимент 1. Абсолютно упругий удар Проведем измерения  для абсолютно упругого удара тележек и запишем данные в таблицу 2. для абсолютно упругого удара тележек и запишем данные в таблицу 2.Таблица 2 Результаты измерений и расчетов для абсолютно упругого удара
Рассчитаем кинетические энергии системы до и после соударения по формулам  Полученные значения занесем в таблицу 2. Вывод: Кинетическая энергия до и после соударения остается примерно одинаковой, с разницей не более 0,4. Эксперимент 2. Абсолютно неупругий удар ( 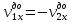 ) )Вывод формулы для относительной величины тепловой энергии δ при  Вывод формулы для δ при β=-1 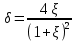 Проведем измерения  и расчет ξ, и расчет ξ,  и и 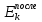 для абсолютно неупругого удара тележек при для абсолютно неупругого удара тележек при 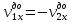 и запишем данные в таблицу 3. и запишем данные в таблицу 3.Таблица 3 Результаты измерений и расчетов для абсолютно неупругого удара
Рассчитаем  по формуле по формуле Рассчитаем  по выведенной формуле и внесем значения в таблицу 3. по выведенной формуле и внесем значения в таблицу 3.Построим график зависимости δ(ξ). 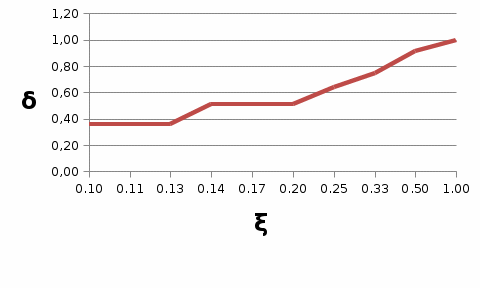 Вывод. Значение относительной величины тепловой энергии пропорционально значению ξ Эксперимент 3. Абсолютно неупругий удар при m1 = m2. Вывод формулы для относительной величины тепловой энергии δ при m1 = m2 Вывод формулы для δ при ξ=1  Проведем измерения  и расчет β, и расчет β,  и и 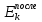 для абсолютно неупругого удара тележек при m1 = m2 и запишем данные в таблицу 4. для абсолютно неупругого удара тележек при m1 = m2 и запишем данные в таблицу 4.Таблица 4 Результаты измерений и расчетов для абсолютно неупругого удара
Рассчитаем  по формуле по формуле Рассчитаем  по выведенной формуле и внесем значения в таблицу 3. по выведенной формуле и внесем значения в таблицу 3.Построим график зависимости δ(β). 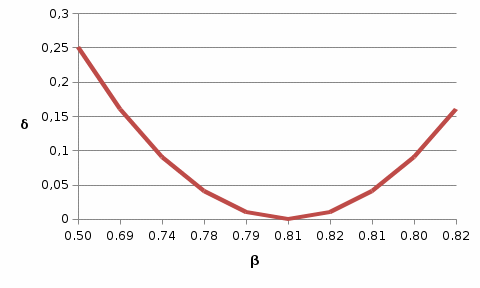 Вывод. Зависимость гиперболическая. Сначала убывает, потом возрастает | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

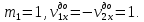

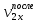 , м/с
, м/с