раздел 1. Электромагнетизм 1 Магнитное поле

• Название: Электромагнетизм 1 Магнитное поле
• Дата: 05.11.2021
• Размер: 1.08 Mb.
• Имя файла: раздел 1.doc
• Тип: Документы; #263619

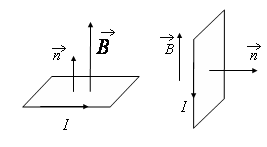
Раздел 6. ЭЛЕКТРОМАГНЕТИЗМ
6.1 Магнитное поле
Магнитное поле – силовое поле, посредством которого осуществляются магнитные взаимодействия. Источниками магнитного поля являются магниты и движущиеся электрические заряды (электрические токи). Магнитное поле проявляется в действии на магниты, движущиеся электрические заряды, проводники или рамки с электрическим током.

Магнитная индукция – векторная величина, характеризующая магнитное поле и определяющая силу, действующую на движущуюся заряженную частицу со стороны магнитного поля. Единица измерения магнитной индукции – тесла: В = Тл. Графически магнитное поле изображается при помощи силовых линий.
Магнитные силовые линии (линии магнитной индукции) – это кривые, касательная к которым в каждой точке совпадает с направлением вектора магнитной индукции в этой точке. Силовые линии магнитного поля всегда замкнуты, что означает отсутствие в природе магнитных зарядов. Если силовая линия перпендикулярна плоскости чертежа, то используются такие обозначения:

- вектор магнитной индукции направлен от нас;

- вектор магнитной индукции направлен к нам.

Однородное магнитное поле – это поле, в каждой точке которого вектор магнитной индукции постоянен как по величине, так и по направлению.

Если в магнитное поле поместить вещество, то магнитная индукция при этом изменится. Вещества, в которых происходит увеличение магнитной индукции , называются ферромагнетиками (железо, кобальт, никель).
Магнитная проницаемость ферромагнетика  – это величина, показывающая во сколько раз увеличивается индукция магнитного поля в присутствии этого вещества:

B = B₀;  >> 1, (1)

где B₀ – магнитная индукция в отсутствие ферромагнетика. Для вакуума (воздуха)  = 1.
6.2 Магнитные силы
Сила Лоренца – векторная величина, представляющая собой силу, которая действует на заряженную частицу, движущуюся со скоростью в магнитном поле. Модуль этой силы

F_Л = q Bsin , (2)
где q – заряд частицы;  - ее скорость; В - индукция магнитного поля; - угол между направлением скорости и вектором магнитной индукции (силовой линией). Направление силы Лоренца, действующей на положительно заряженную частицу, определяется по правилу левой руки.
Правило левой руки: если расположить левую руку так, чтобы линии индукции магнитного поля входили в ладонь, а вытянутые пальцы указывали направление скорости движения положительного заряда, то отогнутый на 90⁰ большой палец укажет направление силы Лоренца. Поскольку ее направление всегда перпендикулярно плоскости, в которой лежат вектор скорости и вектор магнитной индукции, сила Лоренца не совершает работы, а только искривляет траекторию движения заряженных частиц.
Сила Ампера – это сила, с которой однородное магнитное поле действует на проводник с электрическим током. Модуль этой силы
F_A = I Bsin , (3)
где I – сила тока в проводнике;  - его длина; - угол между направлением тока (вектором длины проводника) и вектором магнитной индукции. Вектор силы Ампера всегда перпендикулярен плоскости, в которой находятся проводник и вектор индукции магнитного поля; направление этой силы соответствует правилу левой руки.
На плоский замкнутый контур с током, помещенный в однородное магнитное поле, действует механический момент сил, оказывающий на рамку ориентирующее действие. Модуль вращающего момента

M = ISBsin , (4)
где I – сила тока в контуре; S - площадь, охватываемая контуром; - индукция магнитного поля; - нормаль к плоскости контура (вектор единичной длины, перпендикулярный этой плоскости); - угол между нормалью и вектором магнитной индукции.

Контур с током в магнитном поле а) б) Рис.1.

Когда векторы и параллельны (рис.1.а), вращающий момент сил равен нулю, и виток находится в положении устойчивого равновесия. Если векторы и взаимно перпендикулярны (рис. 1.б), то на контур с током действует максимальный момент сил: Мmax = I SB.

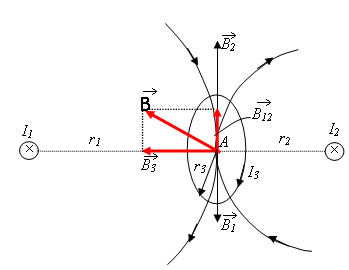
6.3. Электромагнитная индукция
Магнитный поток Ф (поток магнитной индукции) однородного магнитного поля с индукцией В через плоскую поверхность площадью S определяется выражением:

Ф = BScos (5)

Единица измерения магнитного потока – вебер: Ф = Вб.

Магнитный поток (потосцепление) через поперечное сечение одинаковых плотно сжатых витков (катушка) находится следующим образом:

, (6)

где N – число витков в катушке; Ф - магнитный поток через один из ее витков.

Явление электромагнитной индукции состоит в том, что при изменении магнитного потока, пронизывающего контур, в нем возникает сторонняя электродвижущая сила (ЭДС) индукции, вызывающая появление индукционного тока. ЭДС индукции _i и сила индукционного тока I_i - алгебраические величины: их знак определяется относительно заранее выбранного положительного направления обхода контура.

Закон электромагнитной индукции (закон Фарадея): ЭДС индукции, возникающая в контуре, пропорциональна скорости изменения магнитного потока, пронизывающего этот контур, т.е.

_i =  (7)

Здесь Ф = Ф₂ Ф₁ обозначает приращение магнитного потока за время t, где Ф₂ и Ф₁ есть, соответственно, конечное и начальное значения магнитного потока. Знак минус в законе (7) обусловлен соглашением о том, что положительное направление обхода контура и направление нормали к плоскости контура связаны между собой по правилу правого винта.

Согласно правилу Ленца индукционный ток имеет такое направление, при котором создаваемое им магнитное поле препятствует любому изменению магнитного потока, вызывающего индукционный ток.

Если за время t магнитный поток изменился от значения Ф₁ до значения Ф₂ и закон его изменения неизвестен, то по формуле (7) можно вычислить лишь среднее значение ЭДС индукции. В случае равномерного изменения магнитного потока выражение (7) дает точное (неизменное во времени) значение ЭДС индукции.

Согласно выражению (5), простейшими причинами, вызывающими изменение магнитного потока, являются следующие:

1) изменение магнитной индукции В по величине;

2) изменение угла между вектором магнитной индукции и нормалью к плоскости контура (вращение витка);

3) изменение площади S, охватываемой контуром.

Если в неизменяющемся магнитном поле движется прямолинейный проводник, то возникающую в нем ЭДС индукции также можно рассчитать по формуле (7), где под Ф нужно теперь понимать магнитный поток через площадь, «заметенную» (пересекаемую) за время t проводником при его движении. Так для проводника длиной , движущегося со скоростью  перпендикулярно линиям индукции однородного магнитного поля из выражения (7) следует

 _i = B (8)

Электрический ток, протекая по замкнутому контуру, создает магнитное поле, силовые линии которого пронизывают площадь, охватываемую этим контуром. Магнитный поток Ф сквозь этот виток пропорционален силе текущего по нему тока I:

Ф = LI, (9)

где L – коэффициент пропорциональности, называемый индуктивностью контура. Единица измерения индуктивности – генри: L =Гн. Индуктивность контура (проводника) зависит от его размеров, формы, и магнитных свойств среды, в которой он находится.

Индуктивность катушки (соленоида):

L =

где N – общее число витков в катушке;

S – площадь поперечного сечения катушки;

 - длина катушки;

– относительная магнитная проницаемость среды;

₀ = 12,5610^7 - магнитная постоянная.

Явление самоиндукции – это явление возникновения ЭДС самоиндукции в контуре при изменении силы электрического тока, текущего по этому контуру. Если индуктивность проводника неизменна (L = const), то ЭДС самоиндукции пропорциональна скорости изменения силы электрического тока:

 _i =  (10)

Здесь I = I₂  I₁ обозначает приращение силы тока за время t, где I₂ и I₁ есть, соответственно, конечное и начальное значения силы тока в проводнике.

В пространстве, где существует магнитное поле, распределена энергия. Энергия магнитного поля, создаваемого проводником с индуктивностью L, по которому течет ток силой I, находится по формулам:

W_м = , (11)

где Ф – магнитный поток сквозь замкнутый контур с током.

Объёмная плотность энергии магнитного поля _м – это энергия единицы объёма магнитного поля:

_м = = = ,

где V =   S– объём катушки;

H – напряжённость магнитного поля в катушке, H =

Примеры решения задач
МАГНЕТИЗМ
Задача 1.

По двум бесконечно длинным прямолинейным проводникам, находящимся на расстоянии 50 см друг от друга, в одном направлении текут токи I₁ и I₂ силой по 5 А. Между проводниками на расстоянии 30 см от первого расположен кольцевой проводник с током I₃ силой 5 А (рис. 3). Радиус кольца 20 см. Определить индукцию и напряженность магнитного поля, создаваемого токами в центре кольцевого проводника.

Дано: I1 = I2 = I3 = I = 5 А r1 = 0,3 м r3 = 0,2 м	Решение: В соответствии с принципом суперпозиции индукция результирующего магнитного поля в точке А равна: , (1) где и – индукции полей, создаваемых соответст-
В - ? , Н - ?
венно токами I1 и I2, направленными за плоскость рисунка; - индукция поля, создаваемая кольцевым током.
Как видно из рис. 3 векторы и направлены по одной прямой в противоположные стороны, поэтому их сумма В1 + В2 = В12равна по модулю В12 = В2 – В1 (2) Индукция поля, создаваемого бесконечно длинным проводником с током, ; , (3) где 0 – магнитная постоянная;  - магнитная проницаемость среды (для воздуха  = 1); r1, r2 - расстояния от проводников центра кольца. Подставив уравнение (3) в урав-нение (2), получим:

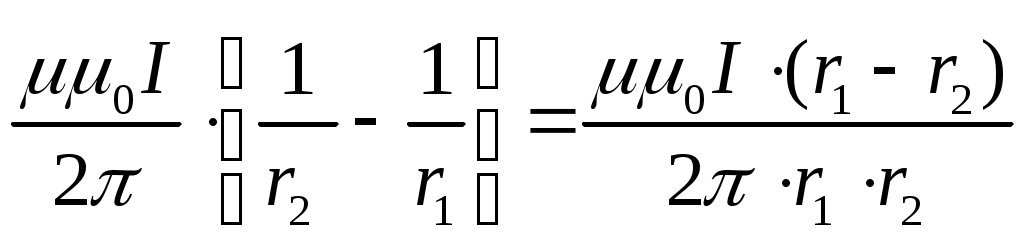В₁₂ = (4)

Индукция поля, создаваемого кольцевым проводником с током, равна:

В₃ = , (5)

где r₃ – радиус кольца.

Как видно из рис.3 векторы и 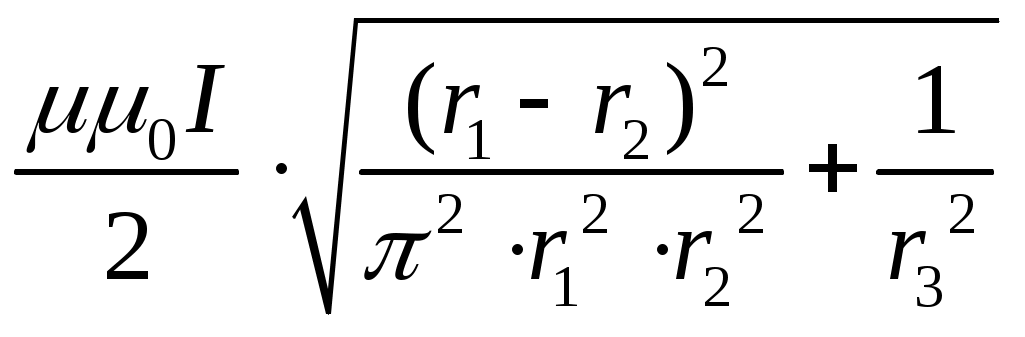взаимно перпендикулярны, поэтому или, учитывая выражения (4) и (5), имеем:

B =

B = 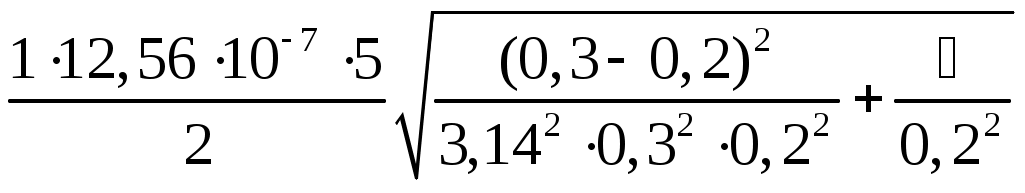= 15,710⁶ Тл = 15,7 мкТл

Напряженность магнитного поля Н = ; Н = = 12,5 А/м.

Ответ: В = 15,7 мкТл; Н = 12,5 А/м

Задача 2.
Электрон, пройдя ускоряющую разность потенциалов 88 кВ, влетает в однородное магнитное поле с индукцией 0,01Тл перпендикулярно силовым линиям. Определить радиус траектории электрона.

Дано: U = 88 кВ В = 0,01 Тл Е = 1,61019 Кл	Решение: В магнитном поле с индукцией на электрон, движущийся со скоростью перпендикулярно , действует сила Лоренца F = eB, (1) которая обусловливает центростремительное ускорение электрона при его движении по окружности:
r - ?

eB = , (2)

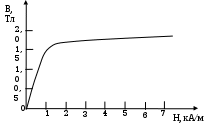
где m – масса электрона; е - его заряд; r - радиус траектории его движения.
Пройдя ускоряющую разность потенциалов U, электрон приобретает кинетическую энергию , равную работе А сил электрического поля = еU. Отсюда находим скорость электрона:

 =

Из уравнения (2) с учетом уравнения (3) найдем радиус траектории:

r =

r = 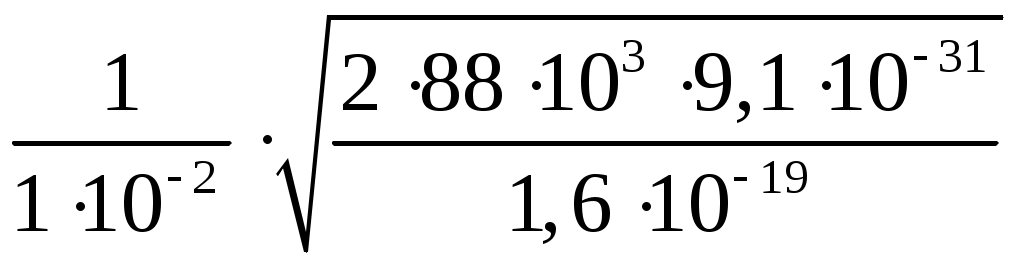= 0,1 м

Ответ: r = 0,1 м

Задача 3.
Соленоид длиной 20 см и диаметром 4 см имеет плотную трехслойную обмотку из провода диаметром 0,1 мм. По обмотке соленоида течет ток силой 0,1 А. Зависимость для материала сердечника приведена на рис.4. Определить напряженность и индукцию поля в соленоиде, магнитную проницаемость сердечника, индуктивность соленоида, энергию и объемную плотность энергии поля соленоида.

Дано:  = 0,2 м D = 0,04 м N = 3 d = 1104 м I = 0,1 A	Решение: Поле внутри соленоида можно считать однородным. В этом случае напряженность поля равна: H = In, (1) где I – сила тока в обмотке. n = (2) n число витков, приходящихся на единицу длины соленоида; N - число слоев обмотки; d  диаметр провода.
H, B, , L, W,  ?

Тогда

H =

H = = 3000 А/м.

По графику B = f (H) находим, что напряженности 3000 А/м соответствует индукция 1,7 Тл. Используя связь между индукцией и напряженностью: B = 0 H (3) определим магнитную прони-цаемость:  =  = = 450

Рис. 4

Индуктивность соленоида:

L = ₀ n²S, (4)

где  – длина; S = – площадь поперечного сечения соленоида.

Учитывая уравнение (2), получим:

L = ₀  (5)

L = = 128 Гн

Объемная плотность энергии магнитного поля  =

 = = 2250 Дж/м³

Энергия магнитного поля соленоида: W = S, (6)

или W = (7)

Проверка размерности:
Подставив числовые значения, получим:

W = 12810^2  0,5 = 0,64 Дж
Ответ: H = 3000 А/м; B = 1,7 Тл;  = 450; L = 128 Гн; = 2,55кДж/м³; W = 0,64 Дж

Задача 4.
На соленоид (см. условие и решение задачи 3) надето изолированное кольцо того же диаметра. Определить электродвижущую силу индукции в кольце и электродвижущую силу самоиндукции в соленоиде, если за 0,01 с ток в его обмотке равномерно снижается до нуля.

Дано: B = 1,7 Тл D = 0,04 м I1 = 0,1 А I2 = 0 L = 128 Гн t = 102 c  i ,  s  ?	Решение: По условию за время t = 0,01 c сила тока в обмотке соленоида равномерно уменьшается от 0,1 А до нуля, поэтому магнитный поток, пронизывающий площадь кольца S = , уменьшается от Ф1 = BS до Ф2 = 0. Электродвижущая сила индукции, возникающая в кольце равна: i = 

_i = = 0,2 В

Электродвижущая сила самоиндукции _s, возникающая в соленоиде при выключении в нем тока равна: _s =  L .
Так как при выключении сила тока уменьшается до нуля равномерно, то



Тогда _s =

_s = = 1280 В

Ответ: _i = 0,2 В; _s = 1280 В.
Задача 5.
Виток радиусом 5 см с током 1 А помещен в однородное магнитное поле напряженностью 5000 А/м так, что нормаль к витку составляет угол 60 с направлением поля. Какую работу совершат силы поля при повороте витка в устойчивое положение?

Дано: r = 0,05 м I = 1 А H = 5000 А/м  = 60	Решение: Работа А при повороте витка с током I в магнитном поле равна: А = I Ф (1) гдеФ = Ф2 – Ф1 – изменение магнитного потока сквозь площадь витка S = r 2 ; Ф1 = В Scos - магнитный поток, пронизывающий виток в начальном положении, где  – угол между векторами и .
А = ?

Устойчивым положением витка в магнитном поле является такое, при котором направление нормали к нему совпадает с вектором индукции, т.е. cos = 1. Следовательно, Ф₂ = ВS. Таким образом, Ф = Вr ²(1  cos). Учитывая, что B = ₀H, имеем:
Ф = ₀ H r²(1  cos) (2)

Подставляя уравнение (2) в уравнение (1), получим:

А = I₀Hr² (1  cos)

А = 112,5610^7  510³  3,142510^4  (1 – 0,5) = 2,46 10^5 Дж
Ответ: А = 2,4610^5 Дж.

Задачи для самостоятельного решения.

1. Ток силой I = 50 А течет по проводнику, согнутому под прямым углом. Найти напряженность Н магнитного поля в точке, лежащей на биссектрисе этого угла и отстоящей от вершины угла на расстояние b = 20 см. Считать, что оба конца проводника находятся очень далеко от вершины угла.

2. По контуру в виде равностороннего треугольника течет ток силой I = 50 А. Сторона треугольника а = 20 см. Определить магнитную индукцию В в точке пересечения высот.

3. Очень короткая катушка содержит N = 1000 витков тонкого провода. Катушка имеет квадратное сечение со стороной длиной а = 10 см. Найти магнитный момент p_m катушки при силе тока I = 1 А.

4. Электрон движется в однородном магнитном поле перпендикулярно линиям индукции. Определить силу F, действующую на электрон со стороны поля, если индукция поля B = 0,2 Тл, а радиус кривизны траектории R = 0,2 см.

5. Протон и -частица, ускоренные одинаковой разностью потенциалов, влетают в однородное магнитное поле. Во сколько раз радиус R₁ кривизны траектории протона больше радиуса R₂ кривизны траектории -частицы?

6. Сколько ампер-витков потребуется для создания магнитного потока 0,42 Вб в соленоиде с железным сердечником длиной 120 см и площадью поперечного сечения 3 см².

7. Круговой контур помещен в однородное магнитное поле так, что плоскость контура перпендикулярна к направлению магнитного поля. Напряженность магнитного поля 150 кА/м. По контуру течет ток 2 А. Радиус контура 2 см. Какую работу надо совершить, чтобы повернуть контур на угол  = 90⁰ вокруг оси, совпадающей с диаметром контура.

8. Тонкий медный провод массой m = 5 г согнут в виде квадрата и концы его замкнуты. Квадрат помещен в однородное магнитное поле (B = 0,2 Тл) так, что его плоскость перпендикулярна линиям поля. Определить заряд q, который потечет по проводнику, если квадрат, потянув за противоположные вершины, вытянуть в линию.

9. С помощью реостата равномерно увеличивают силу тока в катушке на I = 0,1 А в 1 с. Индуктивность L катушки равна 0,01 Гн. Найти среднее значение э.д.с. самоиндукции _S .

10. По проводнику, изогнутому в виде кольца радиусом R = 20 см, содержащему N = 500 витков, течет ток силой I = 1 А. Определить объемную плотность  энергии магнитного поля в центре кольца.