Фазовые равновесия
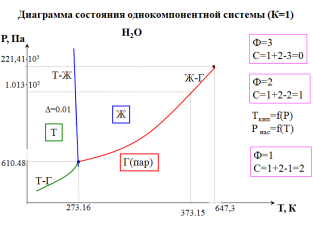
Правило фаз Гиббса: число степеней свободы гетерог многокомп сис-мы, на кот f +из внеш факторов, оказ влияние только Т и Р = число компон минус число фаз плюс два. С=k-f+2. В общем случае C = k – f +n. С=1моновариантная сис-ма; С=2бивариант; С=0 нонвариантрная
Однокомпонентые сис-мы: нужно знать T,P,V. Любые 2 пар-ра – независимые, 3й – их функция.
Принцип соответствия: каждому фазовому сост сис-мы на диагр отвечает опред геом образ: точка, кривая, часть пл-сти.
Ф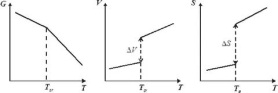 азовые переходы 1 рода: обыч превр агрегат состояний. Характ скачкообраз измен плотности(молярного объёма, S, G) Изобарный потенциал 1 кол-ва вва в 2х фазах одинаков азовые переходы 1 рода: обыч превр агрегат состояний. Характ скачкообраз измен плотности(молярного объёма, S, G) Изобарный потенциал 1 кол-ва вва в 2х фазах одинаков 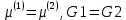 . . 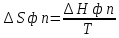 . Ур-е Клаузиуса-Клайперона – завис Т от Р: . Ур-е Клаузиуса-Клайперона – завис Т от Р: 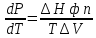 . .
1. Плавление: 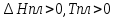 . Знак . Знак 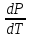 завис от знака V. завис от знака V.
2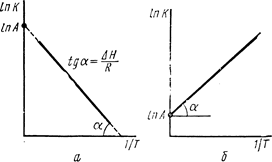 . Испарение: . Испарение: 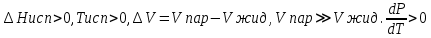 . Темп испар повыш с ростом давления. Примен – перегонка жид с высоким Р. Если счит пар идеаль газом: . Темп испар повыш с ростом давления. Примен – перегонка жид с высоким Р. Если счит пар идеаль газом: 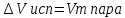 . . 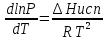 . Проинтегрир ур-е в небольш интерв темп-р, так что S можно счит пост: . Проинтегрир ур-е в небольш интерв темп-р, так что S можно счит пост: 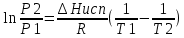
3. Возгонка: 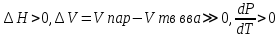 . . 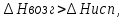 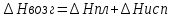 . Правило Трутона: мольная энтальпия испар в норм т кипения (1атм) приблизит постоянна, . Правило Трутона: мольная энтальпия испар в норм т кипения (1атм) приблизит постоянна, 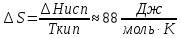 . .
|
Сис-мы необраз хим соединений и тв рров: смеси металлов Cd-Bi; Ac-Si, тв солей KCl – AgCl.
1- Начало крист-и. 2- конец. СЕВ – показ завис Т нач крист от состава – ликвидус. АЕД – завис Т конца крист от состава – солидус. тF: С=2-2+1=1. По мере крист Cd в распл станов всё меньше, состав жид фазы измен по кривой FE. т.E – крист обоих комп (С(Е)=2-3+1=0). Ниже ТЕ сис-ма просто остывает. Е – эвтектика. Рассм жидкую эвтектику 61% Bi. Если 2 комп взаимно не раств в др друге, то присутств второго комп пониж Т нач крист др комп-та(соотв и Тпл). Линия соед составы равновес фаз точки отвеч равнов фазам назыв нода – коннода FP.
Правило Рычага: массы кол-ва равновесных фаз обратно пропорц-ны длинам отрезков, на кот фигур точка делит ноду. 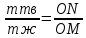 ; ; 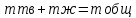
Диаграмма для сис-м с неогранич взаим растворим компон(с образов тв рров) Cu-Ni; Ag-Au; Au-Pd; Co-Ni; Fe-Ni; PbCl2 – SnCl2.
1- Нач крист. 2- конец; АМВ – ликвидус; AFB – coлидус. Между AMB и AFB двухфазное равновесие. Т. m – С = 2-1+1=2; т. М – С=2-2+1. Первые кристаллы обогащены золотом, поэтому при охл в расплаве его будет всё меньше. При достиж TF – т. О: 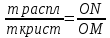 прав Рычага. Используют для разделен комп-тов – зонная плавка. При зонной плавке разделённая смесь помещь в трубку, нагр на узком участке до плавления. Печь передвиг вдоль трубки. Т.о расплавл зона постеп перемещ-ся. По мере её передвиж измен состав слитка: в конеч итоге на одном его конце собир чистый препарат, на др удал примеси. прав Рычага. Используют для разделен комп-тов – зонная плавка. При зонной плавке разделённая смесь помещь в трубку, нагр на узком участке до плавления. Печь передвиг вдоль трубки. Т.о расплавл зона постеп перемещ-ся. По мере её передвиж измен состав слитка: в конеч итоге на одном его конце собир чистый препарат, на др удал примеси. 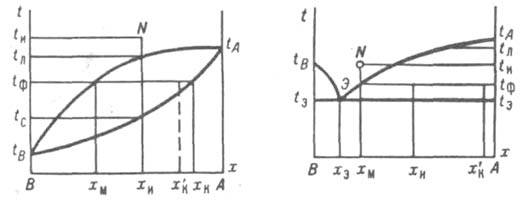
|
Двухкомп сис-мы, образ хим соед, плавящиеся конгруэнтно(без разложения): МЕ1СЕ2Р – ликвидус; FG, G2O – cолидус, Е1 – эвтектика Mg + PbMg2. E2- эвтектика Pb + PbMg2.
Cис-мы с огранич растворимостью в твёрд состоянии: т. 1 – С=2; т.2 – С=2-2+1=1. По мере крист тв рров, обогащ Pb, его содерж в жид фазе уменьш, состав расплава при этом измен по кривой 2Е; состав тв рра измен по 2N; при достиж TE крист рр Bi в Pb и рр Pb в Bi. тЕ – С=2-3+1=0 .
Сис-мы, образ соед, плавящиеся инконгруэнтно(с разложение): LECK – ликвидус, MNFP – солидус. тС отвеч двум тв фазам: KClтв и тв 2KCl*CuCl, обе фазы обогащены KCl – перетектическая точка, F’ – недостижимая точка.
Дальтониды и бертоллиды: ФХ анализ показыв, что тв рры часто образованы не на основе чистых комп-ов, а на основе их соед-й, плавящихся конгруэнтно или инконгруэнтно. Дальтониды: хим соед опред состава и образ тв рры (имеется максимум, отвеч действит хим соед-ю). Бертоллиды: соед переменн состава, максимум плавный и не отвеч к-либо простому стехиометрич составу; образ непрочные соед, явл промежут между нетипичными хим соед и тв ррами.
|
Диаграммы растворим в 2х-компон сисмах:
АКВ – бинодаль. тО- расслоение – 2рра. т2: С=2-1+1=2, тО: С=2-2+0. Справедливо пр Рычага.
3х-комп сис-мы: Правило фаз С = 3-f+2 = 5 – f. T,P, N1, N2. Cостав 3х комп сис-мы изобр точкой в треугольнике. Тр Гиббса (тр Розебома)
Диаграмма растворимости:
Диаграмма плавкости в 3х комп сисмах:
|
 Скачать 71.51 Kb.
Скачать 71.51 Kb.