Анализ данных. Экстремумы. финан финансовый университет при правительстве российской федерации
 Скачать 1.04 Mb. Скачать 1.04 Mb.
|
 Федеральное государственное образовательное бюджетное учреждение высшего образования «ФИНАН «ФИНАНСОВЫЙ УНИВЕРСИТЕТ ПРИ ПРАВИТЕЛЬСТВЕ РОССИЙСКОЙ ФЕДЕРАЦИИ» Департамент анализа данных, принятия решений и финансовых технологий О.А.Баюк, С.Я.Криволапов, Т.Л. Мелехина Монотонность и поиск локальных экстремумов функций (Excel) Учебно-методические рекомендации для проведения семинара №8 по компьютерному практикуму Для бакалавров направления 38.03.01 «Экономика» Электронное издание Москва 2017 Монотонность и поиск локальных экстремумов функций (Excel) Введение Возрастающие, невозрастающие, убывающие и неубывающие функции на множестве D называются монотонными на этом множестве, а возрастающие и убывающие – строго монотонными. Интервалы, в которых функция монотонна, называются интервалами монотонности. Необходимые условия возрастания (убывания) функции. Если дифференцируемая на интервале  функция функция  возрастает (убывает), то возрастает (убывает), то  для любого для любого  . .Достаточные условия возрастания (убывания) функции. Если функция  дифференцируема на интервале дифференцируема на интервале  и и  для любого для любого  , то эта функция возрастает (убывает) на интервале , то эта функция возрастает (убывает) на интервале  . .Пример. Исследовать функцию 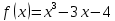 на монотонность. на монотонность.Решение. Функция определена на всей действительной оси:  . Найдем производную функции: . Найдем производную функции: 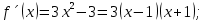 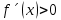 при при  и и  при при  . .Ответ: функция возрастает на интервалах  и убывает на интервале и убывает на интервале 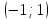 . .Точка  из области определения функции из области определения функции  называется точкой минимума (максимума) этой функции, если найдется такая δ-окрестность называется точкой минимума (максимума) этой функции, если найдется такая δ-окрестность 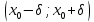 точки точки  , что для всех , что для всех  из этой окрестности выполняется неравенство из этой окрестности выполняется неравенство   . .Точки минимума и максимума называются точками экстремума, а значения функции в этих точках называются экстремумами функции. Понятие экстремума всегда связано с определенной окрестностью точки из области определения функции. Поэтому функция может иметь экстремум лишь во внутренних точках области определения. Если у функции несколько экстремумов, то их называют локальными. Необходимое условие экстремума. Если дифференцируемая функция  имеет экстремум в точке имеет экстремум в точке  , то её производная в этой точке равна нулю: , то её производная в этой точке равна нулю:  . .Геометрически равенство  означает, что в точке экстремума дифференцируемой функции означает, что в точке экстремума дифференцируемой функции  касательная к её графику параллельна оси Ox. касательная к её графику параллельна оси Ox.Однако, обратное неверно, то есть если  , то это не значит, что , то это не значит, что  – точка экстремума. Например, для функции – точка экстремума. Например, для функции  её производная: её производная: 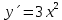 равна нулю при равна нулю при  , но , но  не точка экстремума (в этом можно убедиться по графику функции). не точка экстремума (в этом можно убедиться по графику функции). Существуют функции, которые в точках экстремума не имеют производной. Например, непрерывная функция  в точке в точке  производной не имеет, но точка производной не имеет, но точка  – точка минимума (также можно убедиться по графику функции). – точка минимума (также можно убедиться по графику функции).Таким образом, непрерывная функция может иметь экстремум лишь в точках, где производная функции равна нулю или не существует. Такие точки называются критическими. Достаточное условие экстремума. Если непрерывная функция  дифференцируема в некоторой δ-окрестности критической точки дифференцируема в некоторой δ-окрестности критической точки  и при переходе через неё (слева направо) производная и при переходе через неё (слева направо) производная  меняет знак с плюса на минус, то меняет знак с плюса на минус, то  есть точка максимума; с минуса на плюс, то есть точка максимума; с минуса на плюс, то  – точка минимума. – точка минимума. Исследовать функцию на экстремум означает найти все её экстремумы. Правило исследования функции на экстремум: Найти критические точки функции  ; ;Выбрать из них лишь те, которые являются внутренними точками области определения функции; Исследовать знак производной  слева и справа от каждой из выбранных критических точек; слева и справа от каждой из выбранных критических точек;В соответствии с достаточным условием экстремума выписать точки экстремума (если они есть) и вычислить значения функции в них. Пример. Найти экстремум функции  . .Решение. Очевидно,  . .Находим производную функции  Производная не существует при  и равна нулю при и равна нулю при  . Эти точки разбивают всю область определения на три интервала . Эти точки разбивают всю область определения на три интервала  . Отметим знаки производной слева и справа от каждой из критических точек: . Отметим знаки производной слева и справа от каждой из критических точек:   + ̶ + + ̶ +   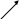 0 8 x 0 8 x Следовательно,  – точка максимума, – точка максимума,  и и  – точка минимума, – точка минимума,  Иногда бывает удобным использовать другой достаточный признак существования экстремума, основанный на определении знака второй производной. Второе достаточное условие экстремума. Если в точке  первая производная функции первая производная функции  равна нулю ( равна нулю ( ), а вторая производная в точке ), а вторая производная в точке  существует и отлична от нуля существует и отлична от нуля 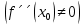 , то при , то при  в точке в точке  функция имеет максимум и минимум – при функция имеет максимум и минимум – при  . .Одним из более эффективных способов нахождения приближённого значения корня является метод касательных. Рассмотрим применение этого метода на примере: С помощью графического метода найти промежуток  , на котором находится действительный корень , на котором находится действительный корень 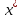 уравнения уравнения 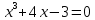 . Пользуясь методом Ньютона, получить приближенное значение корня с точностью до 0,001. . Пользуясь методом Ньютона, получить приближенное значение корня с точностью до 0,001.Краткая геометрическая суть метода состоит в следующем: сначала с помощью специального критерия выбирается один из концов отрезка. Этот конец называют начальнымприближением корня, в нашем примере:  . Теперь проводим касательную к графику функции . Теперь проводим касательную к графику функции  в точке с абсциссой в точке с абсциссой  (синяя точка и фиолетовая касательная): (синяя точка и фиолетовая касательная): Данная касательная пересекла ось абсцисс в жёлтой точке, и обратите внимание, что на первом шаге мы уже почти «попали в корень»! Это будет первое приближение корня  . Далее опускаем жёлтый перпендикуляр к графику функции и «попадаем» в оранжевую точку. Через оранжевую точку снова проводим касательную, которая пересечёт ось ещё ближе к корню! И так далее. Нетрудно понять, что, используя метод касательных, мы довольно быстро приближаемся к цели, и для достижения точности . Далее опускаем жёлтый перпендикуляр к графику функции и «попадаем» в оранжевую точку. Через оранжевую точку снова проводим касательную, которая пересечёт ось ещё ближе к корню! И так далее. Нетрудно понять, что, используя метод касательных, мы довольно быстро приближаемся к цели, и для достижения точности  потребуется буквально несколько итераций. потребуется буквально несколько итераций.Решение. На первом шаге следует отделить корень графически. Это можно сделать путём построения графика  . . Итак, искомый корень принадлежит отрезку  и примерно равен 0,65-0,7. и примерно равен 0,65-0,7.На втором шаге нужно выбрать начальное приближение  корня. Обычно это один из концов отрезка. Начальное приближение должно удовлетворять следующему условию: корня. Обычно это один из концов отрезка. Начальное приближение должно удовлетворять следующему условию: 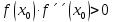 . .Найдём первую и вторую производные функции  : :  В качестве начального приближения выбираем В качестве начального приближения выбираем  . .На третьем шаге нас ожидает дорога к корню. Каждое последующее приближение корня  рассчитывается на основании предшествующих данных с помощью следующей рекуррентной формулы: рассчитывается на основании предшествующих данных с помощью следующей рекуррентной формулы: Процесс завершается при выполнении условия Процесс завершается при выполнении условия  , где , где  – заранее заданная точность вычислений. В результате за приближённое значение корня принимается «энное» приближение: – заранее заданная точность вычислений. В результате за приближённое значение корня принимается «энное» приближение: . .На практике результаты вычислений удобно заносить в таблицу, при этом, чтобы несколько сократить запись, дробь часто обозначают через  : : Сами же вычисления проводим в Excel– это намного удобнее и быстрее. Выполнение работы. Определение областей возрастания и убывания функции. Исследование функции на локальный экстремум. Критические точки. 1.1. Задача. Найти точки локальных экстремумов и области возрастания и убывания функции   Решение: Производная функции:   Построим на листе Excel график функции и ее производной.  Рис. 1.1.1. Построение графика функции. Из графика видно, что  – точка максимума. Т. к., данная функция – нечетная, то – точка максимума. Т. к., данная функция – нечетная, то 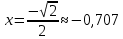 – точка минимума. – точка минимума.Следовательно, интервал возрастания функции (  , ,  ), интервалы убывания функции ), интервалы убывания функции  Ниже рассмотрим два способа более точного определения значений точек экстремума. 1-й способ. Из приведенного выше рисунка 1.1.1 видно, что точка максимума расположена между 0.7 и 0.8. Отметим диапазон B10:D19 и сдвинем его вниз на 10 строк, теперь на освободившемся пространстве в столбце B зададим значения  с шагом 0.01 и вычислим в столбцах С и D значения функции и ее производной. Поступая так же еще необходимое число раз, определим значений точки экстремума с требуемой точностью. с шагом 0.01 и вычислим в столбцах С и D значения функции и ее производной. Поступая так же еще необходимое число раз, определим значений точки экстремума с требуемой точностью. Рис. 1.1.2. Определение точек экстремума. 2-й способ. Использование метода Ньютона (метода касательных) решения уравнений позволяет решить такую задачу.  Рис. 1.1.3. Метод касательных для определения корня производной. Требуется найти корень производной данной функции  , , – начальное приближение, тогда в результате итерационного процесса находятся последующие приближения по формуле – начальное приближение, тогда в результате итерационного процесса находятся последующие приближения по формуле Условие окончания процесса  с компьютерной точностью. В ячейке J34 располагается начальное приближение  , в ячейке K34 - вычисленное значение , в ячейке K34 - вычисленное значение  в ячейке L34 – значение в ячейке L34 – значение  в ячейке M34 – значение в ячейке M34 – значение  , в ячейке N34 – значение , в ячейке N34 – значение  , в ячейку J35 копируется значение , в ячейку J35 копируется значение  для выполнения следующей итерации. Процесс завершается по условию: значение в ячейке N34 равно 0. В данной задаче для выполнения следующей итерации. Процесс завершается по условию: значение в ячейке N34 равно 0. В данной задаче  0.707106781. 0.707106781.3-й способ. Эту задачу можно решить, используя средство Excel «Подбор параметра». Для этого следует выполнить следующие действия. 1. Расположить в первой ячейке начальное приближенное значение x=x0. 2. Во второй ячейке поместить формулу, вычисляющую значение  . .3. Набрать: ДАННЫЕ →Анализ «Что если» → Подбор параметра 4. Задать значения аргументов Установить в ячейке: Адрес второй ячейки Значение: 0 Изменяя значение ячейки: Адрес первой ячейки. Рассмотрим использование указанного средства на примере данной задачи. Требуется найти корень уравнения  при условии, что начальное приближение  . .В ячейку B31 помещаем значение 0,7, в ячейке B32 вычисляем соответствующее значение  . Затем обращаемся к процедуре «Подбор параметра», как показано выше. . Затем обращаемся к процедуре «Подбор параметра», как показано выше.  Рис. 1.1.4. Метод «Подбор параметров» для определения корня производной. Указываем аргументы согласно следующему кадру:  Результат будет представлен в указанных ячейках как представлено на рисунке 1.1.5.  Рис. 1.1.5. Результат метода «Подбор параметров». Следует отметить, что процедура «Подбор параметра» позволяет вычислить подбираемое значение с точностью порядка 0,001. Поэтому, если необходимо получить значение с более высокой точностью, следует использовать метод Ньютона. 1.2. Задача. Найти точки локальных экстремумов и области возрастания и убывания функции  . .Решение: Для функции  областью определения являются областью определения являются  . Вычислим таблицу значений при . Вычислим таблицу значений при  , где , где  , ,  . . 1. Вводим в диапазон ячеек A2:A34 рабочего листа Excel числа  . В ячейку В2 вводим число 0,01. В ячейку В3 вводим формулу В2+0,05. Копируем формулу до ячейки В34. . В ячейку В2 вводим число 0,01. В ячейку В3 вводим формулу В2+0,05. Копируем формулу до ячейки В34. 2. В ячейку С2 вводим формулу =B2*LN(B2). Копируем формулу до ячейки С34. 3. Выделяем диапазон ячеек В2:С34. Задаем команду ВСТАВКА/ДИАГРАММЫ и выбираем тип диаграммы Точечная, как показано на рисунке. Построим на листе Excel график функции и ее производной.  Рис. 1.2.1. Построение графика функции и её производной. Следовательно, интервал возрастания функции (  , ,  ), интервал убывания функции (0; ), интервал убывания функции (0;  ). ). Точка минимума функции  0.367879441 0.3678794411.3. Задача. Найти точки локальных экстремумов и области возрастания и убывания функции  Построим на листе Excel график функции и ее производной.  Рис. 1.3.1. Построение графика функции и её производной. 1.4. Задача. Исследование функции  на локальный экстремум. на локальный экстремум.Найти точки локальных экстремумов и области возрастания и убывания функции  . .Решение: Данная функция четная и периодическая с периодом равным  . Следовательно, ее достаточно исследовать на отрезке длиной, равной половине периода. . Следовательно, ее достаточно исследовать на отрезке длиной, равной половине периода.Используя определение модуля, можно получить другое представление функции:  Следовательно, производная этой функции определяется следующим образом  или  Из последней формулы следует, что производная  обращается в 0 в точках обращается в 0 в точках  Причем в каждой из указанных точек производная меняет знак с плюса на минус, значит указанные точки являются точками максимума, в которых функция достигает значений равных 1. Причем в каждой из указанных точек производная меняет знак с плюса на минус, значит указанные точки являются точками максимума, в которых функция достигает значений равных 1.Кроме того, в точках  производная имеет точки разрыва 1-го рода, в которых ее значение меняется с -1 до 1 (скачки производной), таким образом, в указанных точках функция достигает минимумов, равных 0. Эти точки являются угловыми точками. производная имеет точки разрыва 1-го рода, в которых ее значение меняется с -1 до 1 (скачки производной), таким образом, в указанных точках функция достигает минимумов, равных 0. Эти точки являются угловыми точками.Используя Excel, эту задачу можно решить следующим образом. На листе Excel зададим таблицу значений функции и ее производной на отрезке [-1.8; 3.20], содержащем период этой функции. Пусть при этом значения аргумента x возрастают с шагом  . При этом в диапазоне B9:B259 располагаем указанные значения аргумента, в диапазоне С9:С259 вычисляем соответствующие значения функции с помощью формулы ABS(COS(B9)) с последующим продолжением на остальные ячейки диапазона, в диапазоне D9:B259 - соответствующие значения функции . При этом в диапазоне B9:B259 располагаем указанные значения аргумента, в диапазоне С9:С259 вычисляем соответствующие значения функции с помощью формулы ABS(COS(B9)) с последующим продолжением на остальные ячейки диапазона, в диапазоне D9:B259 - соответствующие значения функции  , в диапазоне E9:E259 - соответствующие значения функции , в диапазоне E9:E259 - соответствующие значения функции  , в диапазоне F9:F259 вычисляем соответствующие значения производной функции с помощью формулы ЕСЛИ(COS(B9)<0, SIN(B9), - SIN(B9)) последующим продолжением на остальные ячейки диапазона. После этого строим графики функции и ее производной (см. Рис. 1.4.1.). , в диапазоне F9:F259 вычисляем соответствующие значения производной функции с помощью формулы ЕСЛИ(COS(B9)<0, SIN(B9), - SIN(B9)) последующим продолжением на остальные ячейки диапазона. После этого строим графики функции и ее производной (см. Рис. 1.4.1.). Рис. 1.4.1. Построение графиков функции и ее производной. На рис. 1.4.2. и 1.4.3 изображены графики функции и ее производной. Из графиков видно, что функция непрерывна, но ее производная имеет точки разрыва 1-го рода.  Рис. 1.4.2. График функции   Рис. 1.4.3. График производной  . .Анализируя графики и учитывая периодичность функции, делаем вывод о том, что в точках  , функция достигает свои максимальные значения, равные 1, а в точках , функция достигает свои максимальные значения, равные 1, а в точках  свои минимальные значения, равные 0. Причем, точки свои минимальные значения, равные 0. Причем, точки  являются угловыми точками графика функции, так как в этих точках производная функции терпит разрыв. Следует обратить внимание на то, что при переходе через все указанные точки производная меняет знак. являются угловыми точками графика функции, так как в этих точках производная функции терпит разрыв. Следует обратить внимание на то, что при переходе через все указанные точки производная меняет знак.Задания для самостоятельной работы. Задача 1. Найти точки локальных экстремумов и области возрастания и убывания функции  Задача 2. Найти точки локальных экстремумов и области возрастания и убывания функции  Задача 3. Найти точки локальных экстремумов и области возрастания и убывания функции  |
