5 Функция_Аналих графических зависимостей. Функция. Анализ графических зависимостей
 Скачать 359.72 Kb. Скачать 359.72 Kb.
|
|
Функция. Анализ графических зависимостей Зависимость переменной y от переменной x называется функцией, если каждому значению х соответствует единственное значение y. Такая зависимость обозначается как y = f(x). При этом х называется независимой переменной (аргументом), y – зависимой переменной (функцией). Графиком функции f(x) называется множество точек (x, y) на плоскости, для которых y = f(x). Область определения функции D(f) – это все значения, которые принимает независимая переменная. Чтобы найти область определения функции, заданной графически, надо спроектировать все точки графика на ось ОХ. Полученный промежуток и будет областью определения функции. Область значения функции Е(f) – это все значения, которые принимает зависимая переменная. Чтобы найти область значения функции, заданной графически, надо спроектировать все точки графика на ось ОY. Полученный промежуток и будет областью значения функции. Нули функции – это значения аргумента х, при которых f(x) = 0. Для функции, заданной графически – это абсциссы точек, в которых график функции пересекает ось абсцисс или касается её. Промежутки знакопостоянства функции – это числовые промежутки, на которых функция сохраняет свой знак, т.е. f(x) > 0, или f(x) < 0. Наибольшим (наименьшим) значением функции на некотором промежутке называется такое значение, которое больше (меньше) всех других значений, принимаемых функцией на данном промежутке. Если функция задана графически, то спроектировав все точки графика на заданном промежутке на ось ОY, получим на этой оси промежуток (a; b), где a – наименьшее, b – наибольшее значение функции. Функция называется возрастающей на некотором промежутке, если большему значению аргумента соответствует большее значение функции, т.е. 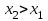 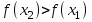 , и называется убывающей, если большему значению аргумента соответствует меньшее значение функции, т.е. , и называется убывающей, если большему значению аргумента соответствует меньшее значение функции, т.е. 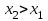 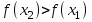 . .Возрастающие и убывающие функции называются монотонными. Числовые промежутки, на которых функция возрастает (убывает) называются промежутками возрастания (убывания). Четность и нечетность. Если для всех xD(f) выполняется: • f(-x) = f(x), то f(x) называется четной; • f(-x) = -f(x), то f(x) называется нечетной. График четной функции симметричен относительно оси ординат, а нечетной функции – относительно начала координат. Ограниченность. Функция f(x) называется ограниченной на некотором промежутке, если существует такое число М > 0, что для всех х из этого промежутка выполняется неравенство |f(x) | M. Периодичность. Функция f(x) называется периодической с периодом Т > 0, если для всех х из области определения функции f(x+ Т) = f(x). Упр. Функция задана графически 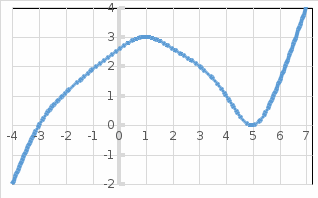 Укажите: а) область определения функции; б) область значения функции; в) промежутки, на которых функция принимает только положительные значения; г) нули функции; д) промежутки возрастания функции; е) найти наибольшее и наименьшее значение функции в области ее определения. ▼ а) Чтобы найти область определения функции, заданной графически, надо спроектировать все точки графика но ось ОХ. Полученный промежуток и будет областью определения функции D(у) = (-4; 7); б) Чтобы найти область значения функции, заданной графически, надо спроектировать все точки графика но ось ОУ. Полученный промежуток и будет областью определения функции Е(у) = (-2; 4); в) Надо найти те промежутки оси ОХ, на которых график функции расположен выше оси ОХ. Положительные значения функция принимает на промежутке (-3; 5) и (5; 7). г) Надо найти те точки, в которых график функции пересекает ось ОХ или касается ее. Нулями функции будут 5 и -3; д) Для определения промежутков возрастания функции можно воспользоваться определением, но для того, чтобы прочитать график, достаточно знать графическую интерпретацию возрастания функции на промежутке: график функции «поднимается вверх». Получаем, что функция возрастает на промежутке (-4; 1] и [5; 7). е) Спроектируем все точки графика на заданном промежутке на ось ОY, получим на этой оси промежуток (-2; 4), где -2 – наименьшее, 4 – наибольшее значение функции. Линейная функция и ее график Линейной функцией называется функция вида y = kx + b, где k, b – числа. Графиком линейной функции является прямая, коэффициент k называется угловым коэффициентом прямой. При k> 0 функция возрастает; при k< 0 – убывает на всей числовой оси. Для построения прямой линии достаточно указать две точки, отсекаемой прямой на координатных осях. Упр. Построить графики функций 1) y = 2x - 4 x = 0 y = -4, (0;-4) y = 0 x = 2, (2; 0)  2) 2x + 3y = 6 x = 0 y = 2, (0; 2) y = 0 x = 3, (3; 0) 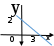 3) y = 2 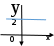 4) x = -1 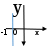 Квадратичная функция и ее график Квадратичной функцией называется функция вида y = ax2 + bx + c, где а, b, c – некоторые числа, a ≠ 0. Графиком квадратичной функции является парабола. График параболы строят по характерным точкам: 1) Расположение ветвей параболы: а > 0 – ветви вверх; а < 0 – ветви вниз. 2) Корни параболы ax2 + bx + c= 0, при этом D > 0 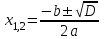 D = 0 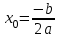 D < 0 действительных корней нет. 3) Координаты вершины параболы (x0, y0): 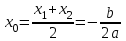 , , 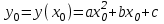 4) Точка пересечения с осью ОУ: у(0) = с 5) Ось симметрии: вертикальная прямая х = х0 Упр. Построить график функции 1) y = x2 - 2x – 3 а = 1 > 0 – ветви вверх Корни: x2 - 2x – 3 = 0 х = -1; 3 Координаты вершины параболы (x0, y0): 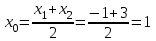 , , 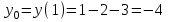 (1, -4) – вершина Ось симметрии: х = 1 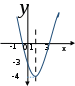 Упр. 1) Прямая y = kx + b пересекает ось ОХ в точке (3; 0), ось ОУ в точке (0; 9). Запишите уравнение этой прямой. Проходит ли эта прямая через точку (-1; 11). ▼ Прямая проходит через две точки, поэтому их координаты (3; 0), (0; 9) удовлетворяют уравнению прямой: 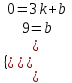 b = 9, k = -3; y = -3x + 9 – уравнение прямой b = 9, k = -3; y = -3x + 9 – уравнение прямой Прямая y = -3x + 9 не проходит через точку (-1; 11), поскольку ее координаты не удовлетворяют уравнению прямой: 11 ≠ -3(-1) + 9 ▲ 2) Парабола y = ax2 + bx + c с вершиной (-1; 2) проходит через точку с координатами (1; 8). Запишите уравнение этой параболы. В каких точках парабола пересекает ось абсцисс. ▼ Уравнению параболы удовлетворяют координаты двух точек (-1; 2), (1; 8). Это значит 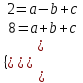 . Кроме того, точка (-1; 2) является вершиной параболы. Это значит: . Кроме того, точка (-1; 2) является вершиной параболы. Это значит: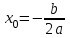 , , 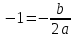 , b = 2a. Итак: , b = 2a. Итак: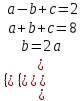 ; ; 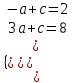 а = 1,5; b= 3; с = 3,5. а = 1,5; b= 3; с = 3,5.Уравнение искомой параболы y = 1,5x2 + 3x + 3,5 Для определения точек пересечения параболы с осью абсцисс решим уравнение 1,5x2 + 3x + 3,5 = 0, D = 9 – 27 < 0 – корней нет, следовательно, парабола не пересекает ось абсцисс▲ 3) При каких значениях k парабола y = 4x2 + 12x + k касается оси абсцисс. ▼ По условию, парабола с осью абсцисс имеет только одну общую точку. Это значит, что уравнение 4x2 + 12x + k= 0 имеет один корень. Это возможно, если D = 144 – 16k = 0, k = 9▲ 4) Прямая х = 2 – ось симметрии параболы y = ax2 + (a2 + 4)x – 4, ветви которой направлены вниз. Найти координаты вершины параболы. ▼ Поскольку х = 2 – ось симметрии параболы, координаты вершины (x0, y0) есть: x0 = 2, y0 = у(2) = 4a + 2(a2 + 4) – 4 = 2a2 + 4a + 4 = 2(a2 + 2a+ 2), где значение а находим по формуле: 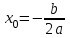 , , 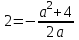 , 4а = -a2 – 4, a2 + 4а + 4 = 0, (а + 2)2 = 0, а = -2 , 4а = -a2 – 4, a2 + 4а + 4 = 0, (а + 2)2 = 0, а = -2Координаты вершины параболы: x0 = 2, y0 = 2(4 – 4 + 2) = 4, т.е. (x0, y0) = (2; 4)▲ 5) Прямая, параллельная прямой у = -4х, касается параболы y = x2 – 2. Найти координаты точки касания. ▼ Из условия параллельности прямой у = -4х и касательной к параболе y = kx + b, получаем уравнение касательной y = -4x + b, где b -? Касательная y = -4x + b и парабола y = x2 – 2 имеют одну общую точку. Это значит, что система уравнений 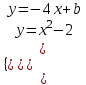 имеют единственное решение. имеют единственное решение.x2 – 2 = -4x + b, x2 + 4x– (b + 2) = 0. Уравнение имеет единственное решение, если D = 0. D = 16 + 4(b + 2) = 24 + 4b = 0, b = -6. Уравнение касательной к параболе y = -4x–6 Координаты точки касания находим из системы: 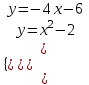 ; x2 – 2 = -4x– 6, x2 + 4x+ 4 = 0, (x+ 2)2 = 0, x= -2; ; x2 – 2 = -4x– 6, x2 + 4x+ 4 = 0, (x+ 2)2 = 0, x= -2;y = 2; (x, y) = (-2, 2) ▲ 6) Построить график функции 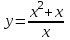 , укажите ее область значений. , укажите ее область значений.▼ 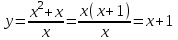 , х ≠ 0 , х ≠ 0E(y) = (-∞; 1)(1; ∞)  7) Построить график функции 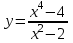 . При каких значениях аргумента функция принимает положительные значения. . При каких значениях аргумента функция принимает положительные значения.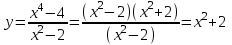 , х ≠ ± , х ≠ ±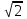 у > 0 при хϵ(-∞; ∞), х ≠ ± 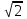 . . 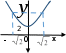 ▲ 8) Построить график функции 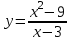 . При каких значениях аргумента выполняется неравенство y > 3. . При каких значениях аргумента выполняется неравенство y > 3.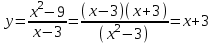 , х ≠ 3 , х ≠ 3у > 3, если х > 0, х ≠ 3.  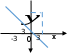 ▲ 9) Построить график функции 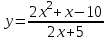 . Найти область значений. . Найти область значений.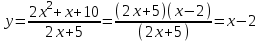 , х ≠ -2,5 , х ≠ -2,5E(y) = (-∞; ∞), у ≠ -4,5.  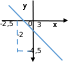 ▲ 10) Постройте график функции ▼Разложим числитель дроби на множители: При её график — парабола c выколотыми точками 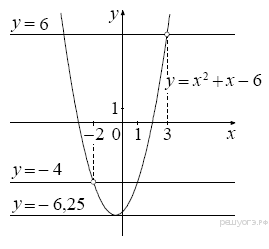 Прямая Поэтому 11) При каком значении ▼ График функции изображён на рисунке. 2. Задание 23 № 127 При каком значении ▼ График функции изображён на рисунке. 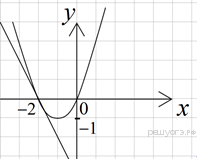 Запишем условие общей точки: Прямая Ответ: p = −4, координата точки: (−2;0).▲ 12) Известно, что парабола проходит через точку ▼Уравнения параболы, вершина которой находится в начале координат: Ответ: 13) Парабола проходит через точки K(0; –5), L(3; 10), M( –3; –2). Найдите координаты её вершины. ▼Одна из возможных форм записи уравнения параболы в общем виде выглядит так: 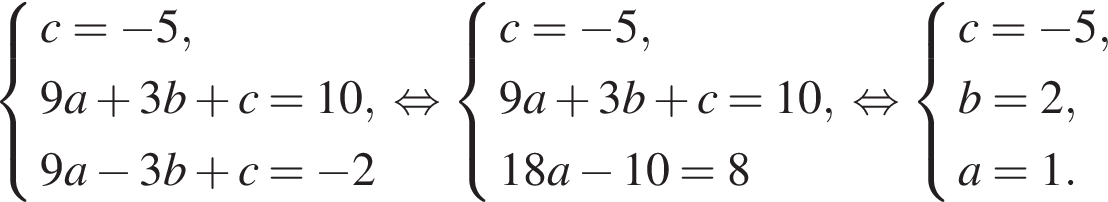 Найдём координаты вершины: Ответ: (−1; −6).▲ 14) При каких значениях ▼Координата Заметим, что первый множитель всегда больше нуля, поэтому на него можно разделить. 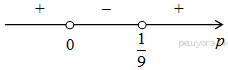 Произведение двух сомножителей будет больше нуля, если сомножители имеют одинаковый знак (см. рисунок). Таким образом, получаем ответ: 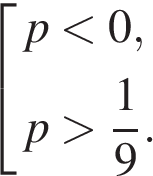 Ответ: 15) При каких значениях p вершины парабол расположены по разные стороны от оси x? ▼ Абсцисса вершины параболы определяется по формуле Ордината Вершины парабол находятся по разные стороны от оси абсцисс, если ординаты их вершин имеют разные знаки. Два множителя имеют разные знаки тогда и только тогда, когда их произведение отрицательно. Тем самым, требуется решить неравенство 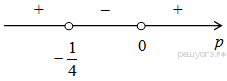 Произведение двух сомножителей больше нуля, если они имеют один и тот же знак (см. рис.). Таким образом, получаем ответ: 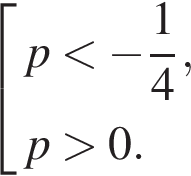 Ответ: 16) Найти все значения а, при которых неравенство x2 + (2a + 4)x + 8a + 1 0 не имеет решения. ▼График функции у = x2 + (2a + 4)x + 8a + 1 – парабола, ветви которой направлены вверх. Данное неравенство не имеет решение, если парабола целиком расположена в верхней полуплоскости, т.е. D < 0, D = (a + 2)2 – (8a + 1) = a2 – 4a + 3 < 0 1 < a < 3 ▲ |
