Шпаргалка. Теория физика лаба 2-1. Где n единичный вектор нормали
 Скачать 115.63 Kb.
|
|
Как известно, электростатическое поле в каждой точке характеризуется двумя физическими величинами: напряженностью  (отношение силы, действующей на помещенный в данную точку поля точечный заряд, к этому заряду) и потенциалом  (отношение потенциальной энергии заряда в поле к этому заряду). Между этими характеристиками существует связь , где (1) (2)Градиент функции  (x,y,z) есть вектор, направленный в сторону максимального возрастания этой функции, а его длинна, равна производной функции  в том же направлении. Поскольку функция  возрастает наиболее быстро в направлении нормали к эквипотенциальной поверхности то формулу (2) можно записать: (3)Где n – единичный вектор нормали. Таким образом, формула (1) показывает, что вектор напряженности электростатического поля в каждой его точке численно равен быстроте изменения потенциала вдоль силовой линии и направлен в сторону убывания потенциала (знак минус). Графически электростатическое поле можно представить либо с помощью силовых линий, либо с помощью эквипотенциальных поверхностей. Силовые линии и эквипотенциальные поверхности взаимно перпендикулярны. (Эквипотенциальная поверхность — геометрическое место точек электростатического поля, имеющих одинаковый потенциал. Свойства эквипотенциальных поверхностей: 1) в каждой точке эквипотенциальной поверхности вектор напряженности электрического поля перпендикулярен к ней и направлен в сторону убывания потенциала; 2) работа по перемещению электрического заряда по эквипотенциальной поверхности равна нулю. Примером эквипотенциальной поверхности является поверхность заряженного проводника.) И 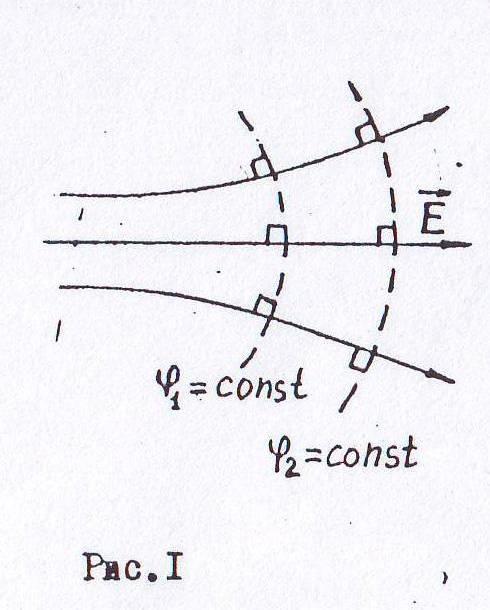 зучить электростатическое поле – это значит определить в каждой точке поля значение вектора  или скаляра  . Формула (1) позволяет определить  в любой точке, если выражение для потенциала задается аналитически. Однако теоретический расчет  и  возможен лишь в случае полей, создаваемых электродами простых конфигураций. Сложные электростатические поля, которые имеют место в электронных приборах, как правило, исследуется экспериментально. Для этого достаточно определить положение эквипотенциальных поверхностей в поле. Если  и  - потенциалы двух близких эквипотенциальных поверхностей, а  - расстояние, отсчитанное по нормали к эквипотенциальным поверхностям (рис. 1), то среднее значение напряженности  на участке  определиться по формуле: (4)В случае полей, обладающих центральной или осевой симметрией:  (5) (6)Для измерения потенциалов используют метод зонда. Электрический зонд представляет собой небольшой остроконечный проводник. Который помещается в ту точку поля, где нужно измерить потенциал. Изучение электростатического поля методом зонда трудно осуществимо. Поэтому для измерений широко используют метод электролитической ванны. Сущность метода заключается в следующем: если потенциалы электродов поддерживать постоянным, а пространство между ними заполнить слабопроводящей жидкостью, то распределение потенциалов в электрическом поле постоянного тока будет тождественным распределению потенциалов между теми же электродами. |