OFDM на Пайтоне. Httpscolab research google comgithubvarun19299wirelesslabiitmblobnotebooks4ofdmpython

Название	Httpscolab research google comgithubvarun19299wirelesslabiitmblobnotebooks4ofdmpython
Дата	31.08.2022
Размер	361.36 Kb.
Формат файла
Имя файла	OFDM на Пайтоне.docx
Тип	Документы #657061

Четверг	[ 11 ] 19:00 - 19:40	Н-ТПР,ЭИТ лек.	МРЭТн-20-1	Онлайн
	[ 12 ] 20:00 - 20:40	Н-ТПР,ЭИТ лек.	МРЭТн-20-1	Онлайн
	[ 13 ] 21:00 - 21:40	Н-ТПР,ЭИТ прак.	МРЭТн-20-1	Онлайн

https://colab.research.google.com/github/varun19299/wireless-lab-iitm/blob/notebooks/4-ofdm-python.ipynb#scrollTo=UFb5wBMH6e5i

https://dspillustrations.com/pages/posts/misc/python-ofdm-example.html

Базовый пример OFDM на Python

В этой записной книжке мы исследуем основные строительные блоки системы OFDM на стороне передатчика и приемника. OFDM (мультиплексирование с ортогональным частотным разделением) - это система с несколькими несущими, которая применяется в широком диапазоне систем беспроводной передачи, таких как LTE, WiMAX, DVB-T и DAB. Фундаментальная концепция системы с несколькими несущими - это разделение потока данных, передаваемых с высокой скоростью, на несколько узких поднесущих с низкой скоростью. Таким образом достигается ряд преимуществ:

Поскольку длительность символа обратно пропорциональна скорости передачи символов, каждая поднесущая имеет относительно длинные символы. Длинные символы устойчивы к замиранию из-за многолучевого распространения, как это происходит в беспроводных системах.
Когда несущая находится в состоянии глубокого замирания из-за частотной избирательности канала (т. Е. Принятая энергия на этой несущей очень мала), теряются только данные на этой поднесущей, а не весь поток.
Системы с несколькими несущими позволяют легко совместное использование ресурсов несколькими пользователями, выделяя разные поднесущие разным пользователям.

Рассмотрим следующую блок-схему, которая содержит основные блоки для системы OFDM: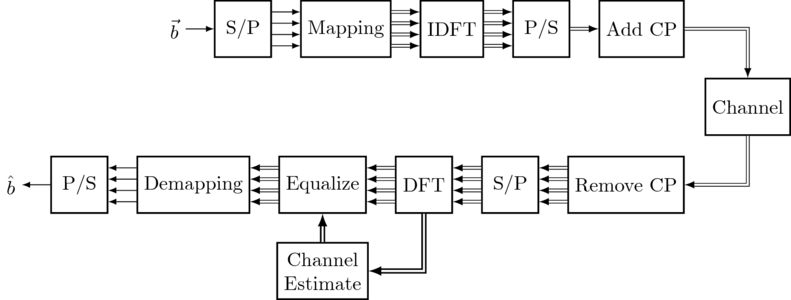

В следующем примере OFDM мы рассмотрим каждый блок и опишем его работу. Однако прежде давайте определим некоторые параметры, которые используются для системы OFDM:

Количество поднесущих KK описывает, сколько поднесущих доступно в системе OFDM.

Запускать код в интерактивном режиме Спрятать

K = 64 # количество поднесущих OFDM

Длина циклического префикса (CP) обозначает количество выборок, которые копируются с конца модулированного блока в начало, чтобы получить циклическое расширение блока. Существует отдельная статья о CP OFDM, в которой его применение рассматривается более подробно.

CP = K // 4 # длина циклического префикса: 25% блока

Количество пилотов ппв символе OFDM описывает, сколько несущих используется для передачи известной информации (то есть пилот-сигналов). Пилоты будут использоваться в приемнике для оценки беспроводного канала между передатчиком и приемником. Кроме того, мы также определяем значение, которое передает каждый пилот (которое известно получателю).

P = 8 # количество пилотных несущих на блок OFDM

PilotValue = 3 + 3 j # Известное значение, которое передает каждый пилот- сигнал

Теперь давайте определим некоторые наборы индексов, которые описывают, какие несущие передают пилот-сигналы, а какие содержат полезную нагрузку.

allCarriers = np . arange ( K ) # индексы всех поднесущих ([0, 1, ... K-1])
PilotCarriers = allCarriers [:: K // P ] # Pilots - этокаждая (K / P) -аянесущая.
# Для удобства оценки канала сделаем последние несущие также пилотными

PilotCarriers = np . hstack ([ pilotCarriers , np . array ([ allCarriers [ - 1 ]])])

P = P + 1
# носителями данных являются все оставшиеся носители

dataCarriers = np . удалить ( allCarriers , pilotCarriers )
print ( "allCarriers: % s " % allCarriers )

print ( "pilotCarriers: % s " % pilotCarriers )

print ( "dataCarriers: % s " % dataCarriers )

plt . plot ( pilotCarriers , np . zeros_like ( pilotCarriers ), 'bo' , label = 'pilot' )

plt . plot ( dataCarriers , np. zeros_like ( носители данных ), 'ro' , label = 'data' )

всеПеревозчики: [0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49

50 51 52 53 54 55 56 57 58 59 60 61 62 63]

PilotCarriers: [0 8 16 24 32 40 48 56 63]

dataCarrier: [1 2 3 4 5 6 7 9 10 11 12 13 14 15 17 18 19 20 21 22 23 25 26 27 28

29 30 31 33 34 35 36 37 38 39 41 42 43 44 45 46 47 49 50 51 52 53 54 55 57

58 59 60 61 62]

Эта статья является частью моего практического руководства по OFDM с использованием дешевой звуковой карты в качестве радио. Если этот блокнот вам интересен, ознакомьтесь с полным руководством !

Определим индекс модуляции μμи соответствующая таблица сопоставления. Мы рассматриваем передачу 16QAM, т.е. имеемμ = 4μзнак равно4бит на символ. Кроме того, отображение групп из 4 битов в символ созвездия 16QAM должно быть определено в mapping_table.

mu = 4 # бит на символ (т.е. 16QAM)

payloadBits_per_OFDM = len ( dataCarriers ) * mu # количество битов полезной нагрузки на символ OFDM
mapping_table = {

( 0 , 0 , 0 , 0 ) : - 3 - 3 j ,

( 0 , 0 , 0 , 1 ) : - 3 - 1 j ,

( 0 , 0 , 1 , 0 ) : - 3 + 3 j ,

( 0 , 0 , 1 , 1 ) : - 3 + 1 J ,

( 0 , 1 , 0 , 0 ) : - 1 - 3 J ,

( 0 , 1 , 0 , 1 ) : - 1 - 1 J ,

( 0 , 1 , 1 , 0 ) : - 1 + 3 J ,

( 0 , 1 , 1, 1 ) : - 1 + 1 j ,

( 1 , 0 , 0 , 0 ) : 3 - 3 j ,

( 1 , 0 , 0 , 1 ) : 3 - 1 j ,

( 1 , 0 , 1 , 0 ) : 3 + 3 J ,

( 1 , 0 , 1, 1 ) : 3 + 1 J ,

( 1 , 1 , 0 , 0 ) : 1 - 3 J ,

( 1 , 1 , 0 , 1 ) : 1 - 1 J ,

( 1 , 1 , 1 , 0 ) : 1 + 3 j ,

( 1 , 1 , 1 ,1 ) : 1 + 1 j

}

для b3 в [ 0 , 1 ]:

для b2 в [ 0 , 1 ]:

для b1 в [ 0 , 1 ]:

для b0 в [ 0 , 1 ]:

B = ( b3 , b2 , b1 , b0 )

Q = mapping_table [ B ]

plt. участок ( Q . реальный , Q . ека , 'б' )

PLT . Текст ( Q . реальный , Q . емк + 0,2 , "" . присоединиться ( ул ( х ) для х в B ), га = 'центр' )

Выше мы изобразили созвездие 16QAM вместе с битовыми метками. Обратите внимание на отображение Грея, т.е. два соседних символа созвездия отличаются только одним битом, а остальные 3 бита остаются такими же. Этот метод помогает минимизировать битовые ошибки в случае обнаружения неправильного символа созвездия: Скорее всего, символьные ошибки являются ошибками "разнесения на один", то есть обнаруживается символ рядом с правильным символом. Тогда возникает только одна битовая ошибка.

Таблица обратного сопоставления - это просто обратное сопоставление таблицы сопоставления:

demapping_table = { v : k для k , v в map_table . items ()}

Давайте теперь определим беспроводной канал между передатчиком и приемником. Здесь мы используем двухотводный многолучевой канал с заданной импульсной характеристикой channelResponse. Также мы строим соответствующую частотную характеристику. Как видим, канал частотно-избирательный. Далее мы определяем отношение сигнал / шум в дБ, которое должно иметь место на приемнике.

channelResponse = np . array ([ 1 , 0 , 0.3 + 0.3 j ]) # импульсная характеристика беспроводного канала

H_exact = np . fft . fft ( channelResponse , K )

plt . сюжет ( allCarriers , abs ( H_exact ))
SNRdb = 25 # отношение сигнал / шум в дБ на приемнике

Теперь, когда мы определили необходимые параметры для нашего примера OFDM, давайте рассмотрим блоки в системе OFDM. Пересмотрите блок-схему:

Все начинается со случайной битовой последовательности бб. Мы генерируем соответствующие биты с помощью случайного генератора, который извлекает из распределения Бернулли ср = 0,5пзнак равно0,5, т.е. 1 и 0 имеют равную вероятность. Обратите внимание, что распределение Бернулли является частным случаем биномиального распределения , когда рассматривается только один розыгрыш (п = 1пзнак равно1):

биты = np . случайный . биномиальное ( n = 1 , p = 0,5 , size = ( payloadBits_per_OFDM , ))

print ( "Количество битов:" , len ( бит ))

print ( "Первые 20 бит:" , биты [: 20 ])

print ( "Среднее значение бит (должно быть около 0,5): " , np . mean ( биты ))

Количество бит: 220

Первые 20 бит: [0 0 1 0 1 0 0 1 1 1 0 1 0 1 1 1 1 1 1 0]

Среднее значение бит (должно быть около 0,5): 0,518181818182

Эта статья является частью моего практического руководства по OFDM с использованием дешевой звуковой карты в качестве радио. Если этот блокнот вам интересен, ознакомьтесь с полным руководством !

Теперь bitsони отправляются в последовательно-параллельный преобразователь, который группирует биты для кадра OFDM в группым тымты биты (т.е. одна группа для каждой поднесущей):

def SP ( биты ):

биты возврата . reshape (( len ( dataCarriers ), mu )) bits_SP = SP ( биты ) print ( «Первые 5 битовых групп» ) print ( bits_SP [: 5 ,: ])

Первые 5 битных групп

[[0 0 1 0]

[1 0 0 1]

[1 1 0 1]

[0 1 1 1]

[1 1 1 0]]

Теперь группы битов отправляются картографу. Устройство отображения преобразует группы в комплексные символы созвездия в соответствии с расширением mapping_table.

def Mapping ( биты ):

вернуть np . array ([ map_table [ tuple ( b )] для b в битах ])

QAM = Mapping ( bits_SP )

print ( "Первые 5 символов и битов QAM:" )

print ( bits_SP [: 5 ,: ])

print ( QAM [: 5 ])

Первые 5 символов и битов QAM:

[[0 0 1 0]

[1 0 0 1]

[1 1 0 1]

[0 1 1 1]

[1 1 1 0]]

[-3. + 3.j 3.-1.j 1.-1.j -1. + 1.j 1. + 3.j]

Следующим шагом (который не показан на схеме) является выделение разных поднесущих с данными и пилот-сигналами. Для каждой поднесущей мы определили, передает ли она данные или пилот-сигнал массивами dataCarriersи pilotCarriers. Теперь, чтобы создать общие данные OFDM, нам нужно поместить данные и пилотные данные на носители OFDM:

def OFDM_symbol ( QAM_payload ):

symbol = np . zeros ( K , dtype = complex ) # общий

символ K поднесущих[ PilotCarriers ] = pilotValue # выделить

символ пилотных поднесущих [ dataCarriers ] = QAM_payload # выделить пилотные поднесущие

возвратный символ

OFDM_data = OFDM_symbol ( QAM )

print ("Количество несущих OFDM в частотной области:" , len ( OFDM_data ))

Количество несущих OFDM в частотной области: 64

Теперь содержащиеся в нем несущие OFDM OFDM_dataмогут быть преобразованы во временную область с помощью операции IDFT.

def IDFT ( OFDM_data ):

вернуть np . fft . IFFT ( OFDM_data )

OFDM_time = ОДПФ ( OFDM_data )

печати ( "Количество выборок OFDM во временной области до CP:" , Len ( OFDM_time ))

Количество отсчетов OFDM во временной области до CP: 64

Впоследствии мы добавляем к символу циклический префикс. Эта операция объединяет копию последних CPвыборок сигнала OFDM во временной области с началом. Таким образом достигается циклическое расширение. КП выполняет две задачи:

Он изолирует разные блоки OFDM друг от друга, когда беспроводной канал содержит несколько путей, т.е. является частотно-избирательным.
Превращает линейную свертку с каналом в круговую. Только с круговой сверткой мы можем использовать одноотводную эквализацию, которой так знаменит OFDM.

Для получения дополнительной информации о CP вы можете обратиться к специальной статье о циклическом префиксе в OFDM .

def addCP ( OFDM_time ):

cp = OFDM_time [ - CP :] # взять последние отсчеты CP ...

вернуть np . hstack ([ cp , OFDM_time ]) # ... и добавьте их в начало

OFDM_withCP = addCP ( OFDM_time )

print ( "Количество отсчетов OFDM во временной области с CP:" , len ( OFDM_withCP ))

Количество отсчетов OFDM во временной области с CP: 80

Теперь сигнал отправляется на антенну и отправляется по воздуху на приемник. Между обеими антеннами находится беспроводной канал. Мы моделируем этот канал как статический многолучевой канал с импульсной характеристикой channelResponse. Следовательно, сигнал на приемной антенне представляет собой свертку передаваемого сигнала с характеристикой канала. Кроме того, мы добавляем к сигналу некоторый шум в соответствии с заданным значением SNR:

канал def ( сигнал ):

convolved = np . скручивать ( сигнал , channelResponse )

signal_power = нп . mean ( abs ( свернутый ** 2 ))

sigma2 = signal_power * 10 ** ( - SNRdb / 10 ) # вычислить мощность шума на основе мощности сигнала и SNR

print ( "Мощность сигнала RX: % .4f . Мощность шума: % .4f " % ( signal_power , sigma2 ))

# Сгенерировать сложный шум с заданной дисперсией

шума = np . sqrt ( sigma2 / 2 ) * ( np . random . randn ( * свернутый . форма ) + 1 j * np . random . randn ( * свернутый . форма ))

return свернутый + шум

OFDM_TX = OFDM_withCP

OFDM_RX = канал (OFDM_TX )

PLT . рисунок ( figsize = ( 8 , 2 ))

plt . plot ( abs ( OFDM_TX ), label = 'TX signal' )

plt . plot ( abs ( OFDM_RX ), label = 'RX signal' )

plt . легенда ( fontsize = 10 )

plt . xlabel ( 'Время' ); plt .ylabel ( '$ | x (t) | $' );

plt . сетка ( True );

Мощность сигнала RX: 0,2114. Уровень шума: 0,0007

Теперь на приемнике КП снимается с сигнала и появляется окно KK выборки извлекаются из принятого сигнала.

def removeCP ( сигнал ):

возвратный сигнал [ CP :( CP + K )]

OFDM_RX_noCP = removeCP ( OFDM_RX )

После этого сигнал преобразуется обратно в частотную область, чтобы получить доступное значение для каждой поднесущей.

def DFT ( OFDM_RX ):

вернуть np . fft . FFT ( OFDM_RX )

OFDM_demod = ДПФ ( OFDM_RX_noCP )

В качестве следующего шага необходимо оценить беспроводной канал. В целях иллюстрации мы прибегаем к простой оценке канала с нулевым принуждением, за которой следует простая интерполяция. Принцип оценки канала следующий:

Сигнал передачи содержит пилотные значения на определенных пилотных несущих. Эти контрольные значения и их положение в частотной области (то есть индекс контрольной несущей) известны приемнику. Из полученной информации на пилотных поднесущих приемник может оценить влияние беспроводного канала на эту поднесущую (потому что он знает, что было передано и что было получено). Следовательно, приемник получает информацию о беспроводном канале на пилотных несущих. Однако он хочет знать, что произошло на носителях данных. Для этого он интерполирует значения канала между пилотными несущими, чтобы получить оценку канала в несущих данных.

def channelEstimate ( OFDM_demod ):

pilots = OFDM_demod [ pilotCarriers ] # извлечь значения пилот-сигнала из сигнала RX

Hest_at_pilots = pilots / pilotValue # разделить на переданные значения пилот-сигнала

# Выполните интерполяцию между пилотными несущими, чтобы получить оценку

# канала в несущих данных. Здесь мы интерполируем абсолютное значение и номер фазы

отдельно

Hest_abs = scipy . интерполировать . interp1d ( pilotCarriers , abs ( Hest_at_pilots ), kind = 'linear' ) ( allCarriers )

Hest_phase = scipy . интерполировать . interp1d ( pilotCarriers , np . angle ( Hest_at_pilots ), kind = 'linear' ) ( allCarriers )

Hest = Hest_abs * np . exp ( 1 j * Hest_phase )

plt . plot ( allCarriers , abs ( H_exact ), label = 'Correct Channel' )

plt . Стволовые ( pilotCarriers , ABS ( Hest_at_pilots ), ярлык = 'Оценки Пилотных' )

PLT . plot ( allCarriers , abs ( Hest ), label = 'Предполагаемый канал с помощью интерполяции' )

plt . сетка ( True ); plt. xlabel ( 'Индекс оператора связи' ); plt . ylabel ( '$ | H (f) | $' ); plt . легенда ( fontsize = 10 )

plt . ylim ( 0 , 2 )

вернуть Hest

Hest = channelEstimate ( OFDM_demod )

Теперь, когда канал оценивается по всем несущим, мы можем использовать эту информацию на этапе эквалайзера канала. Здесь для каждой поднесущей влияние канала устраняется, так что мы получаем обратно четкие (только зашумленные) символы совокупности.

Защита выравнивающий ( OFDM_demod , Хест ):

возвращение OFDM_demod / Хест

equalized_Hest = уравнительные ( OFDM_demod , Хест )

Следующим шагом (не показан на схеме) является извлечение носителей данных из выровненного символа. Здесь мы отбрасываем пилотные несущие, поскольку они не предоставляют никакой информации, но использовались для процесса оценки канала.

Защиту get_payload ( выравнивание ):

возвращение уравнены [ dataCarriers ]

QAM_est = get_payload ( equalized_Hest )

PLT . сюжет ( QAM_est . real , QAM_est . imag , 'bo' );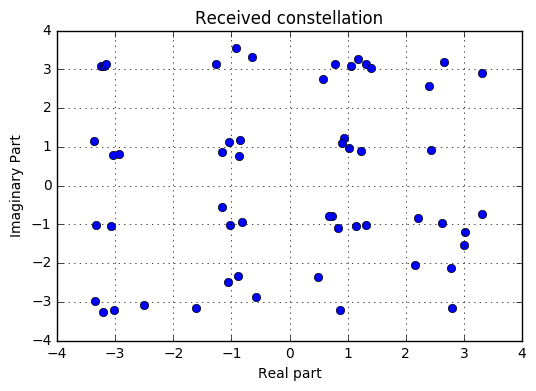

Эта статья является частью моего практического руководства по OFDM с использованием дешевой звуковой карты в качестве радио. Если этот блокнот вам интересен, ознакомьтесь с полным руководством !

Теперь, когда созвездие получено обратно, нам нужно отправить комплексные значения в модуль обратного преобразования, чтобы преобразовать точки созвездия в группы битов. Для этого мы сравниваем каждую полученную точку созвездия с каждой возможной точкой созвездия и выбираем точку созвездия, которая находится ближе всего к полученной точке. Затем мы возвращаем группу битов, принадлежащую этой точке.

def Demapping ( QAM ):

# массив возможных точек

созвездия constellation = np . массив ([ х для й в demapping_table . клавиши ()])

# вычислить расстояние от каждой точки RX до каждой возможной точки

dists = abs ( QAM . reshape (( - 1 , 1 )) - constellation . reshape (( 1 , - 1 )))

# для каждого элемента в QAM выберите индекс в созвездии

#, который принадлежит ближайшей точке созвездия

const_index = dists . argmin ( ось = 1 )

# вернуть реальную точку созвездия

hardDecision = constellation [ const_index ]

# преобразовать точку созвездия в группы битов

return np . vstack ([ demapping_table [ C ] для C в hardDecision ]), hardDecision
PS_est , hardDecision = Demapping ( QAM_est )

для qam , жестко в zip ( QAM_est , hardDecision ):

plt . сюжет ([ кам . реальный , жесткий . реальный ], [ кам . воображаемый , жесткий . воображаемый ], 'б-о' );

plt . сюжет ( hardDecision . real , hardDecision .воображение , ро )

На диаграмме выше синие точки являются полученными точками QAM, тогда как красные точки, связанные с ними, являются ближайшими возможными точками совокупности, и возвращаются группы битов, соответствующие этим красным точкам.

Наконец, группы битов необходимо преобразовать в последовательный поток битов посредством параллельного преобразования в последовательный.

def PS ( биты ):

биты возврата . изменить форму (( - 1 ,)) bits_est = PS ( PS_est )

Теперь, когда все биты декодированы, давайте посчитаем частоту битовых ошибок:

print ( "Полученная частота битовых ошибок:" , np . sum ( abs ( bits - bits_est )) / len ( биты ))

Полученная частота ошибок по битам: 0,0

К счастью, битовых ошибок не произошло, и передача прошла успешно (уменьшите SNR, чтобы получить несколько битовых ошибок)

Эта статья является частью моего практического руководства по OFDM с использованием дешевой звуковой карты в качестве радио. Если этот блокнот вам интересен, ознакомьтесь с полным руководством !

У вас есть вопросы или комментарии? Давайте обсудим ниже!

Поделиться этой статьей

Связанные партнерские продукты

Похожие сообщения

Использование звуковой карты для практического цифрового общения

Циклический префикс (CP) в OFDM

Синхронизация Шмидла и Кокса для OFDM

Далее: Преобразование децибел: коэффициент 10 или коэффициент 20?

Предыдущая: Примеры глазковых диаграмм

Введение

Обо мне

Отпечаток

Конфиденциальность

DSPIllustrations.com является участником программы Amazon Services LLC Associates, партнерской рекламной программы, разработанной для предоставления сайтам средств зарабатывать рекламные сборы за счет рекламы и ссылок на amazon.com, amazon.de, amazon.co.uk, amazon. Это.