Лабораторная работа по теории автоматического управления. ЛРпоТАУАминева5. Исследование автоколебательных режимов в нелинейных системах
 Скачать 198.35 Kb. Скачать 198.35 Kb.
|
|
ФГБОУ ВО Уфимский государственный авиационный технический университет Кафедра ТК Отчет по лабораторной работе №5 по дисциплине «Теория автоматического управления» Вариант 6 Тема: «Исследование автоколебательных режимов в нелинейных системах» Выполнил: ст.гр. УТС-306 Ганеев М.Р. Аминева Р.А. Принял: к.т.н., доц. Саитова Г.А. Уфа 2021 г. Цель работы: экспериментальное и теоретическое исследование условий возникновения периодических автоколебательных режимов в нелинейных системах. Задание: K1=3, K2=6, K3=1, K4=2, K5=1, Т1=0,5, Т2=0,6, B=1, C=1 Ход работы: Нелинейная САУ 2-го порядка Структурная схема нелинейной САУ 2-го порядка и её переходная характеристика представлены на рисунках 1 и 2 соответственно. 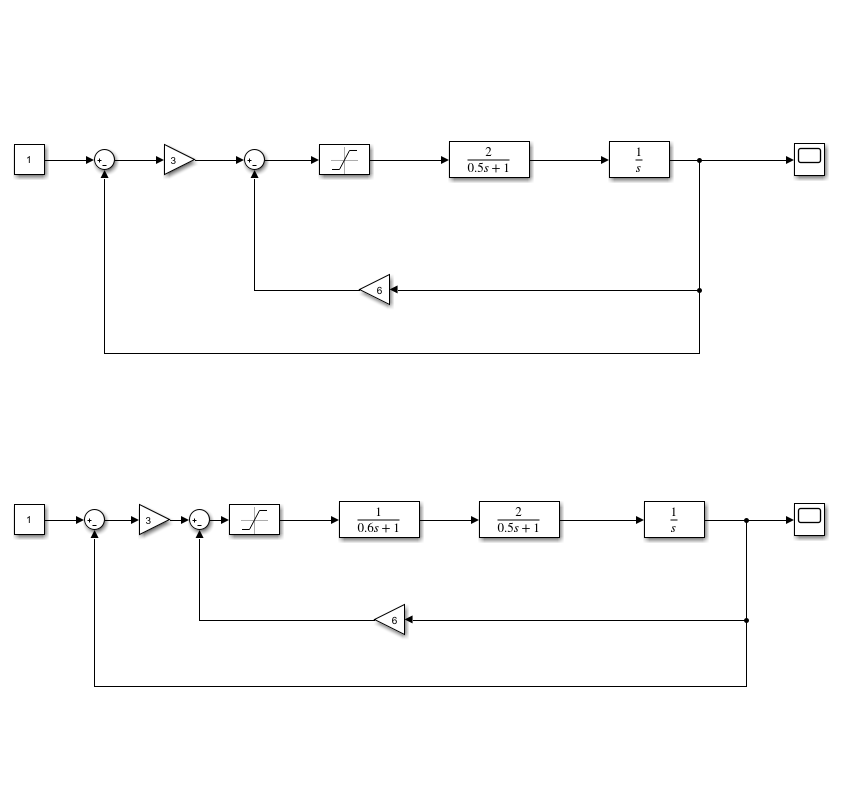 Рисунок 1 – Структурная схема нелинейной САУ 2-го порядка 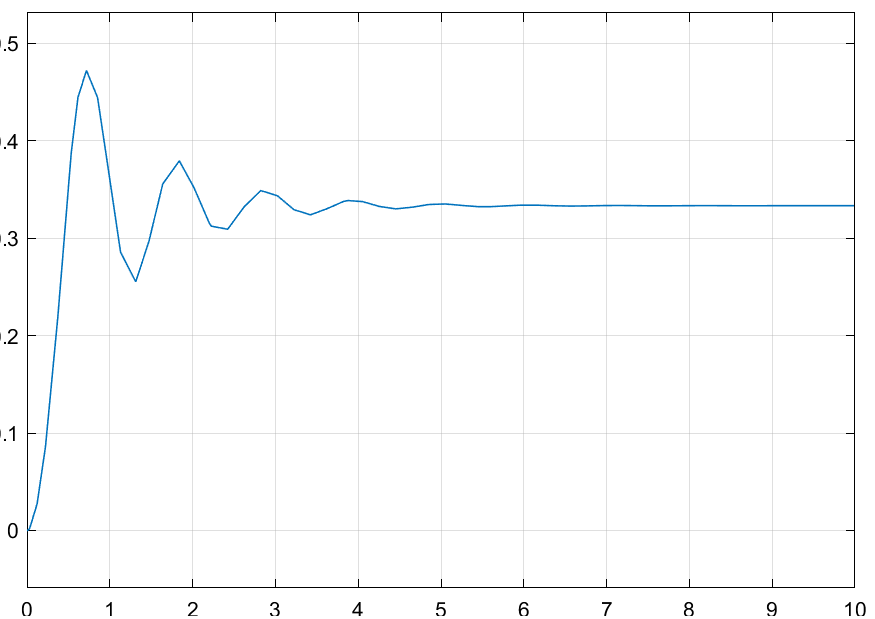 Рисунок 2 – Переходная характеристика нелинейной САУ 2-го порядка Снимем осциллограммы переходных процессов на выходе системы x(t) для различных уровней ступенчатого задающего воздействия g(t). Измерим значения времени регулирования tрег и перерегулирование σ в каждом случае. Результаты измерений представлены в таблице 1. Таблица 1 – Результаты измерений
Нелинейная САУ 3-го порядка Структурная схема нелинейной САУ 3-го порядка представлена на рисунке 3. 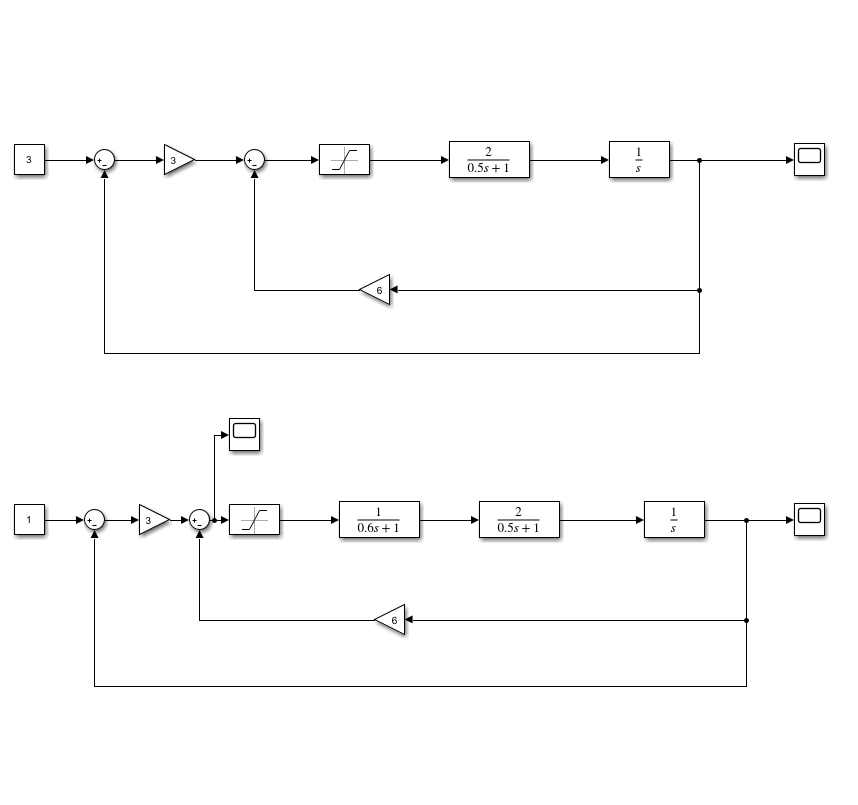 Рисунок 3 – Структурная схема нелинейной САУ 3-го порядка Зарисуем форму автоколебаний на входе нелинейного элемента u(t), полагая: g(t)=0; g(t)=1(t). Результаты представлены на рисунках 4 и 5 соответственно. 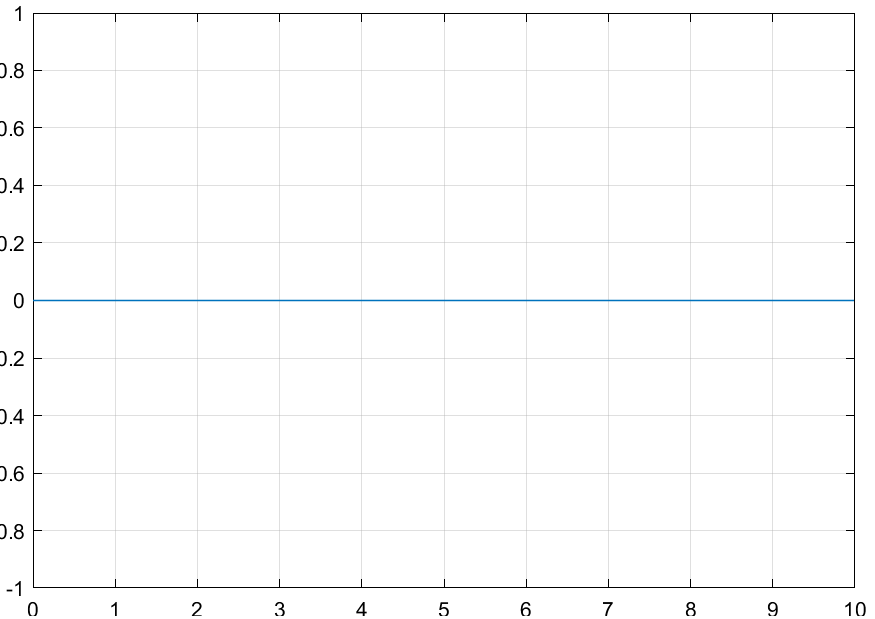 Рисунок 4 – Автоколебания при g(t)=0 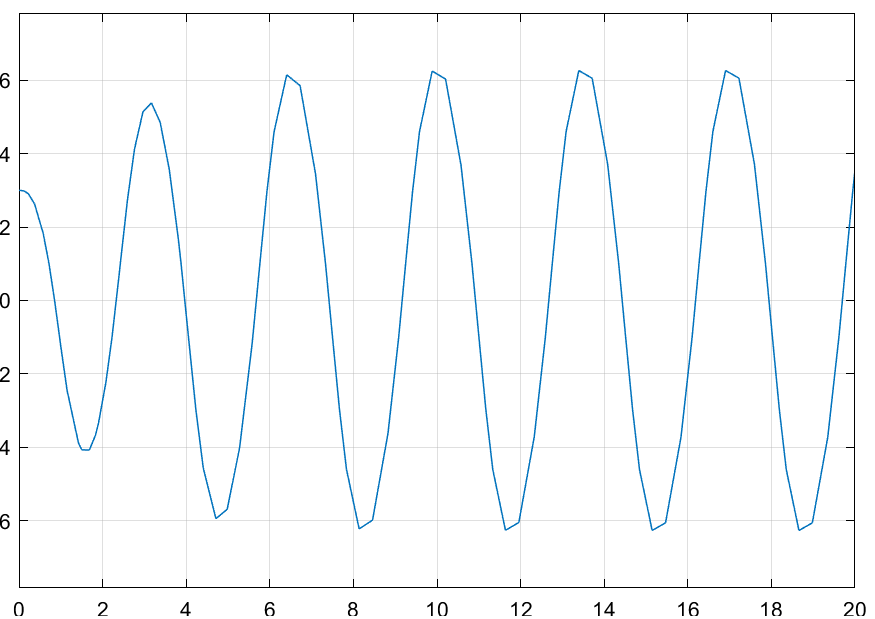 Рисунок 5 – Автоколебания при g(t)=1(t) По рисунку 5 измерим амплитуду и частоту этих автоколебаний. A=6,1; w=1,8 Изменение K4 влияет только на амплитуду. 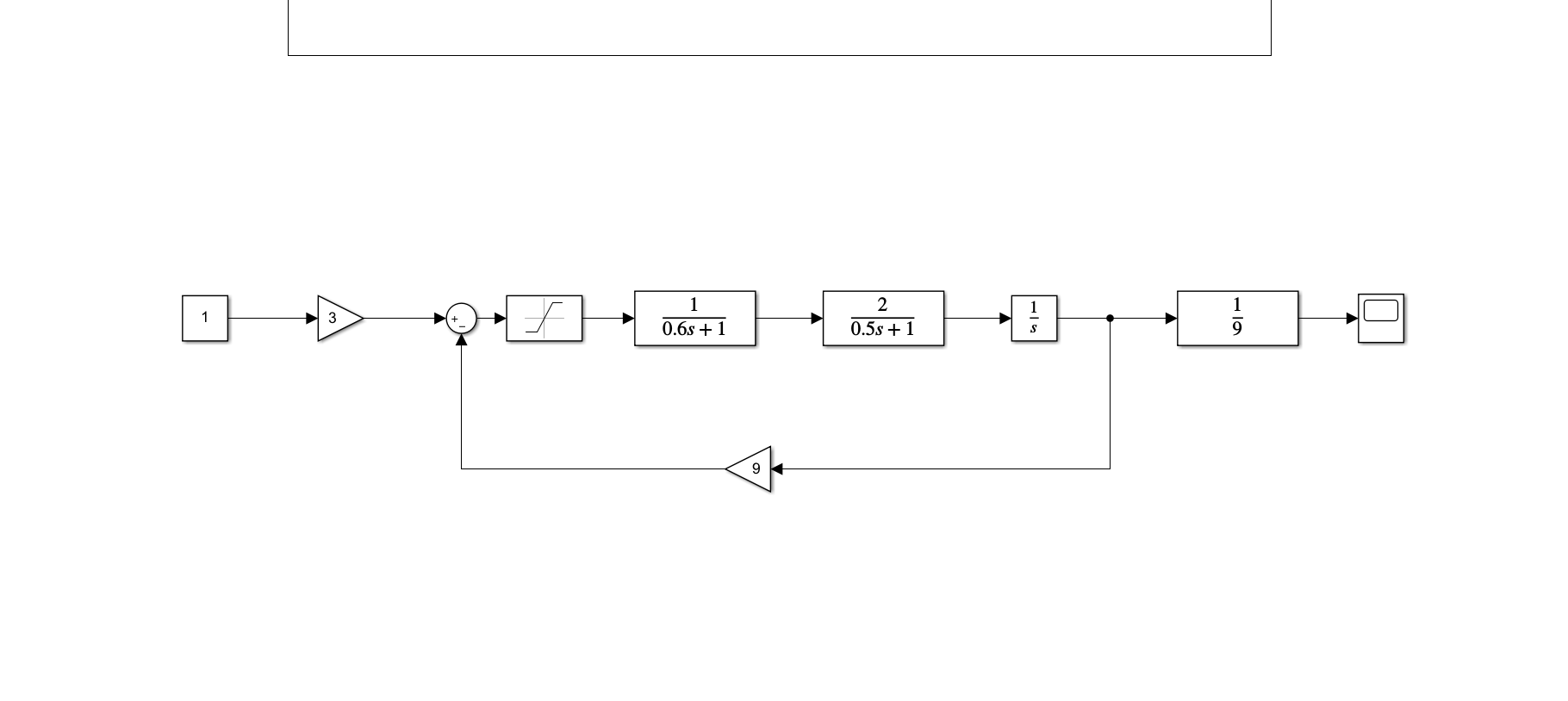 Рисунок 6 – Преобразованная структурная схема Код для решения задачи методом Гольдфарба в Matlab. num=[18]; den=[0.3 1.1 1 0]; sys=tf(num,den) w=1.825:0.01:15; APK=freqs(num, den, w); u=real(APK); v=imag(APK); k=0; for a=6.1:0.1:50,k=k+1; q1=(2/pi)*(asin(1/a)+(1/a)*sqrt(1-(1/(a*a)))); q2=0; fn=-1/(q1+j*q2); ul(k)=real(fn); vl(k)=imag(fn); end plot(u,v,ul,vl);grid 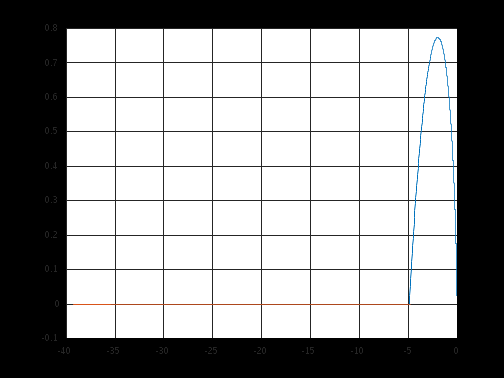 Рисунок 6 – Решение с помощью метода Гольдфарба Методом Гольдфарба мы определили, что амплитуда и частота имеют следующие значения. A=6.1; w=1.825 В данной системе имеются периодические движения. Поскольку нелинейная часть переходит из неустойчивой области в устойчивую, при увеличении амплитуды, то периодические движения устойчивы. В системе имеются автоколебания. Условия получения автоколебаний в такой системе и исходной совпадают. Вывод: в результате выполнения лабораторной работы мы экспериментально и теоретически исследование условий возникновения периодических автоколебательных режимов в нелинейных системах. |

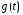
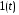
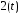
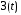
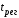 ,c
,c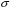 ,%
,%