пз4. ПЗ№4. Исследование влияния радиуса кабеля на напряженность поля у поверхности кабеля, определение распределения потенциала в толще изоляции

• Название: Исследование влияния радиуса кабеля на напряженность поля у поверхности кабеля, определение распределения потенциала в толще изоляции
• Дата: 22.11.2022
• Размер: 144.21 Kb.
• Имя файла: ПЗ№4.docx
• Тип: Исследование; #805760

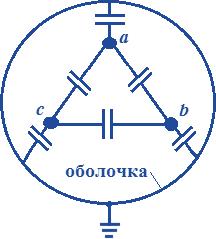
Практическое задание №4

Расчет изоляции кабеля

Цель работы: Расчет емкость кабеля, исследование влияния радиуса кабеля на напряженность поля у поверхности кабеля, определение распределения потенциала в толще изоляции.

Задан одножильный маслонаполненный кабель с заземленной свинцовой оболочкой. Длина кабеля равна l, радиус токоведущей жилы r и радиус оболочки R. Изоляция кабеля имеет диэлектрическую проницаемость _r. Кабель рассчитан на рабочее напряжение U.
Задание: Рассчитать емкость кабеля и определить характер изменения напряженности электрического поля у поверхности токоведущей жилы при увеличении ее радиуса от r до R.

Определить распределение потенциала в толще изоляции при неизменном радиусе внутренней жилы r и построить рассчитанные зависимости E = f(x), j = f(x).
Варианты для расчета приведены в таблице 4.1.

Таблица 4.1 – Варианты задания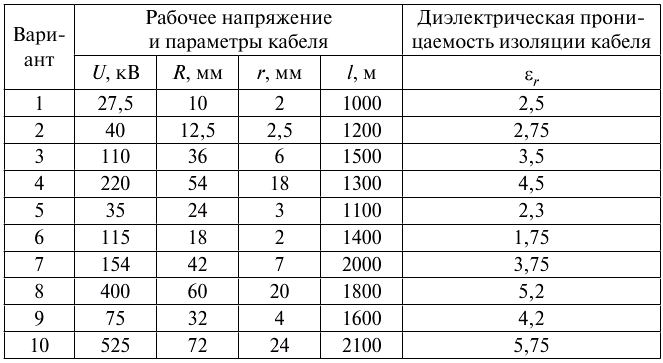



2- Бокенхан Мирас

3 – Болат Ермек

4 – Қашқынбай Ердәулет

5 – Шукруллоев Шукрулло
Методические указания к выполнению задания:

Коаксиальный кабель можно рассматривать как цилиндрический конденсатор (рис.4.1). Известно, что поле цилиндрического конденсатора плоскопараллельное и характеризуется осевой симметрией, причем эквипотенциальные поверхности представляют собой коаксиальные цилиндры.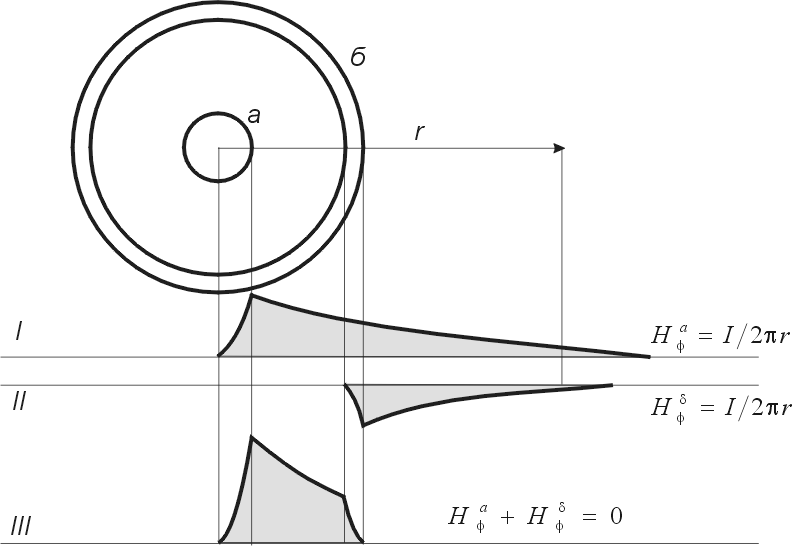


Рисунок 4.1. Распределение напряженности в коаксиальном одножильном кабеле
По теореме Гаусса напряженность электрического поля цилиндрического конденсатора в слое с радиусом r_х равна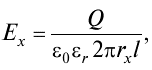



где Q — заряд, ₀ — диэлектрическая проницаемость вакуума,_r — относительная диэлектрическая проницаемость изоляции, r_х — расстояние от токоведущей жилы до точки х, l — длина конденсатора.

Емкость цилиндрического конденсатора определяется по формуле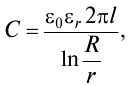


где R — радиус оболочки; r — радиус токоведущей жилы; l — длина кабеля; ε_r — относительная диэлектрическая проницаемость изоляции кабеля; ε₀— диэлектрическая проницаемость вакуума.

Учитывая, что заряд равен произведению емкости на напряжения и подставив выражение для емкости в теорему Гаусса, получаем расчетную формулу для напряженности электрического поля на расстоянии r_х от поверхности токоведущей жилы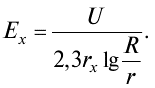

Схемы замещения и параметры кабельных линии.

В схемах замещения выделяют продольные элементы – сопротивления линии электропередачи: 𝑍 = 𝑅 + 𝑗𝑋 и поперечные элементы – проводимости: 𝑌 = 𝐺 + 𝑗𝐵. Значения этих параметров для КЛ определяются по общему выражению
П = П₀𝐿,
где П₀{r₀, x₀, g₀, b₀} – значение продольного или поперечного параметра, отнесенного к 1 км линии (погонные параметры);

𝐿 – протяженность линии электропередачи.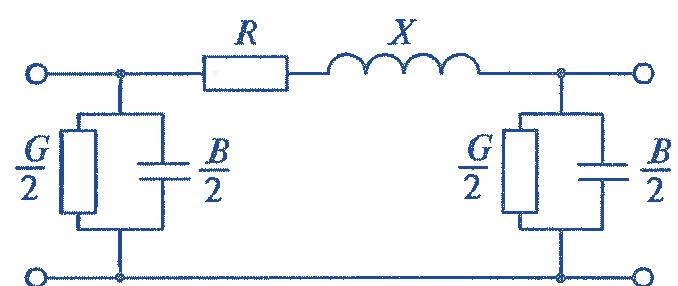

R – активное сопротивление;

X – индуктивное сопротивление;

G – активная проводимость;

B – емкостная проводимость.
Погонное активное сопротивление







0,004 – температурный коэффициент электрического сопротивления, 1/град (для медных и алюминиевых проводов значение α = 0,00403).

Погонное индуктивное сопротивление КЛ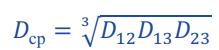



– среднегеометрическое расстояние между фазами;

Для 0,3-10 кВ Х₀ 0,060,10 Ом/км.

Погонная емкостная проводимость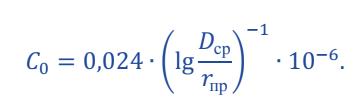



Для КЛ 0,4-10 кВ С₀ ∙ 10⁻⁶

Напряжение, кВ	Сечение жилы, мм2
	10	16	25	35	50	70	95	120	150	185	240
До 1 кВ	0,35	0,40	0,50	0,53	0,63	0,72	0,77	0,81	0,86	0,86	–
6	0,20	0,23	0,28	0,31	0,36	0,40	0,42	0,46	0,51	0,53	0,58
10	–	–	0,23	0,27	0,29	0,31	0,32	0,37	0,44	0,45	0,60

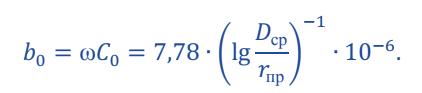Емкостной ток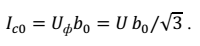



Погонная активная проводимость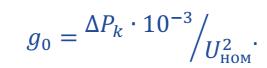



P_k– потери активной мощности.