Теория электрических цепей. Классический метод расчета переходных процессов
 Скачать 168.52 Kb. Скачать 168.52 Kb.
|
|
Расчет переходных процессов в электрических цепях КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ Ключ К2 находится в положении 1. В цепи действует источник напряжения 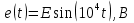 . .Переходный процесс возникает вследствие размыкания ключа К1. Построить графики 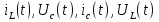 . .Исходные данные: 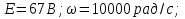 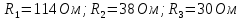 . .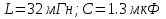  Решение: 1. Расчет состояния до коммутации в момент времени 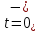 . .До коммутации ключ К1 замкнут – сопротивление 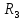 закорочено. закорочено.Напряжение на конденсаторе: 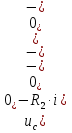 Перейдем к комплексным переменным. Ток в цепи: 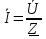 Комплексное напряжение, приложенное к цепи: 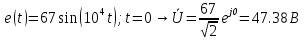 Комплексное сопротивление цепи: 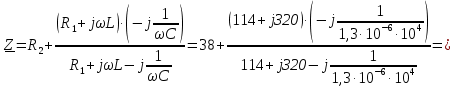 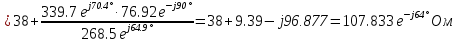 Полный ток в цепи: 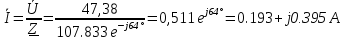 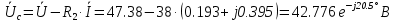  Ток через индуктивность: 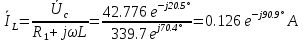 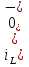 2. Расчет установившегося после коммутации режима. Ключ К1 разомкнут. Напряжение на конденсаторе в установившемся режиме: 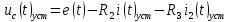 Перейдем к комплексным переменным. Ток в цепи: 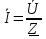 Комплексное напряжение, приложенное к цепи: 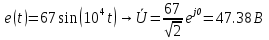 Комплексное сопротивление цепи: 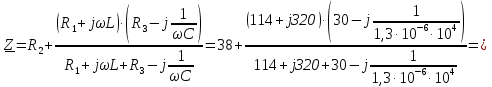 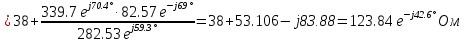 Полный ток в цепи: 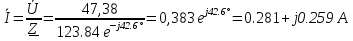 Ток через индуктивность: 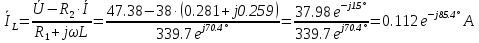 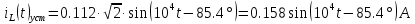 Напряжение на конденсаторе в установившемся режиме: 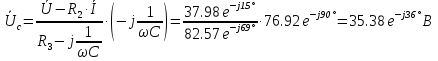 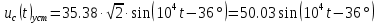 3. Окончательные выражения Составим характеристическое уравнение (после коммутации): 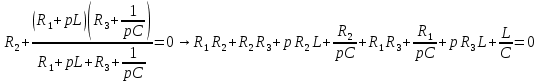 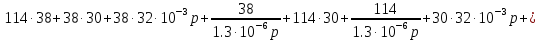 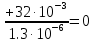 Откуда 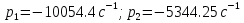 Окончательные выражения будем искать в виде: 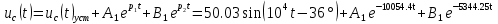 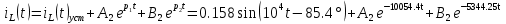 По законам коммутации: 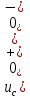 и и 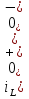 Тогда для напряжения на конденсаторе: 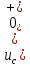 Ток через конденсатор: 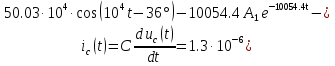 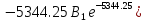 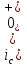 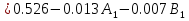 Согласно пункту 2 полный ток в цепи после коммутации: 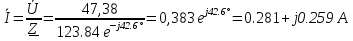   Таким образом, получили систему уравнений: 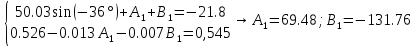 Напряжение и ток на конденсаторе: 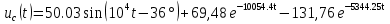 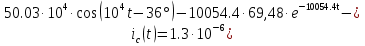 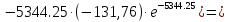 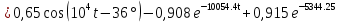 Ток через индуктивность: 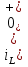 Напряжение на индуктивности: 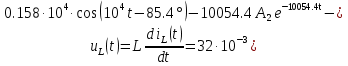 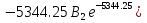 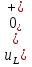 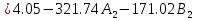 С другой стороны: 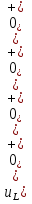 Таким образом, получили систему уравнений: 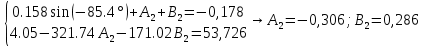 Напряжение и ток на индуктивности: 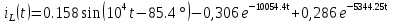 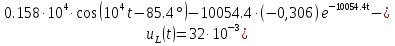 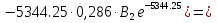 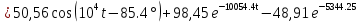 В итоге: 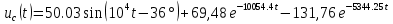 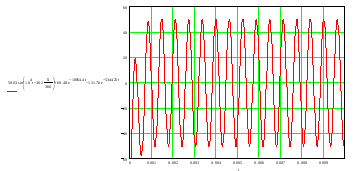 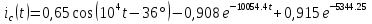 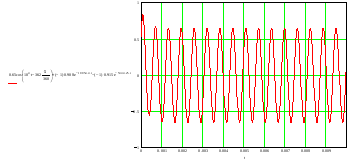 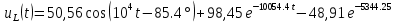 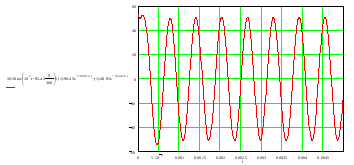 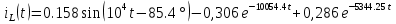 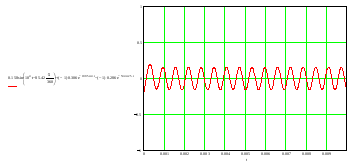 ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ Операторным методом рассчитать переходный ток в индуктивности 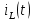 и напряжение на емкости и напряжение на емкости 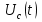 при следующих условиях: в цепи действует постоянный источник напряжения. при следующих условиях: в цепи действует постоянный источник напряжения.Ключ К1 разомкнут, а ключ К2 переводится из положения 1 в положение 2. Построить графики 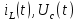 от времени. от времени.Исходные данные: 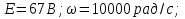 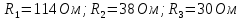 . .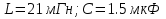  Решение: 1) Независимые начальные условия: 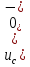 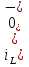 (до коммутации ток через конденсатор не течет) 2) Составим схему замещения:  Составим систему уравнений по законам Кирхгофа: 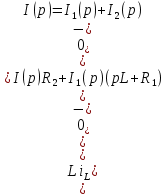 В численном виде: 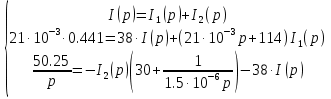 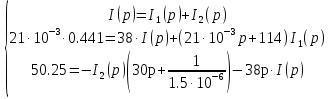 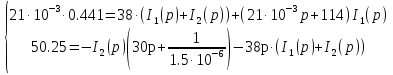 Из первого уравнения: 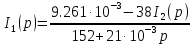 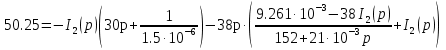 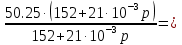 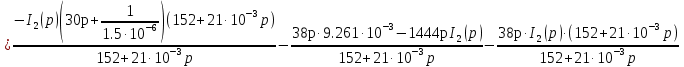 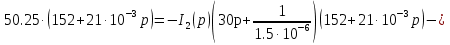 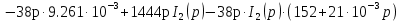 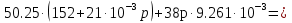 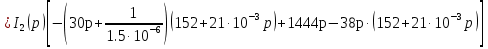 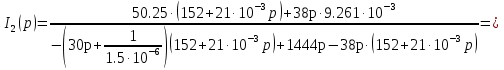 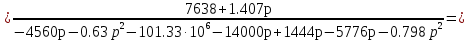 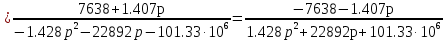 Изображение напряжения на конденсаторе: 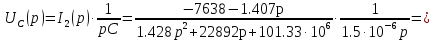 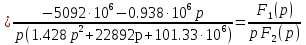 Для перехода от изображения 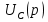 оригиналу оригиналу 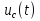 используем формулу разложения: используем формулу разложения: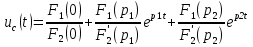 где 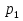 и и 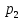 – корни уравнения – корни уравнения 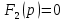 . .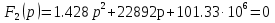 Уравнение 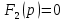 совпадает с характеристическим уравнением данной схемы, значит, расчет выполнен верно. совпадает с характеристическим уравнением данной схемы, значит, расчет выполнен верно.Характеристическое уравнение (после коммутации): 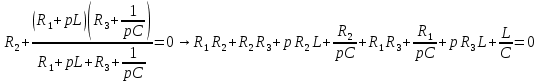 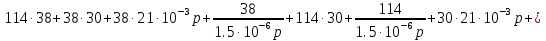 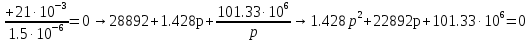 Корни 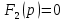 : : 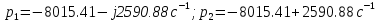 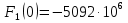 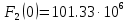 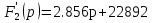 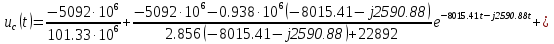 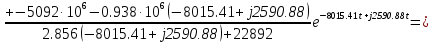 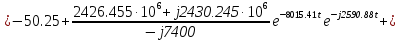 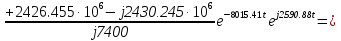 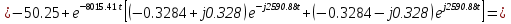 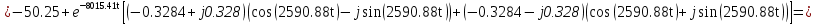 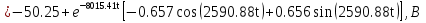 Изображение тока через катушку: 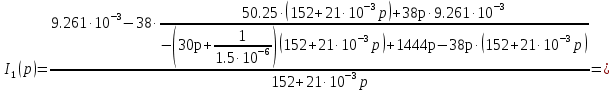 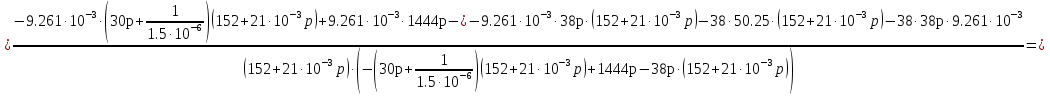 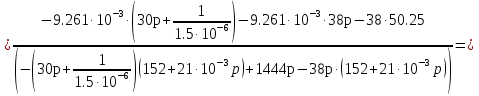 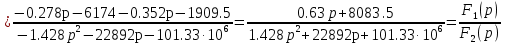 Для перехода от изображения 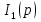 оригиналу оригиналу 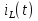 используем формулу разложения: используем формулу разложения: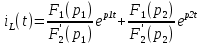 где 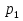 и и 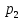 – корни уравнения – корни уравнения 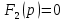 . .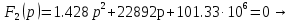 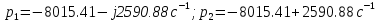 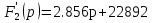 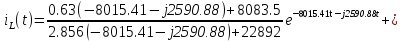 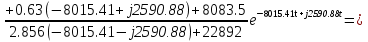 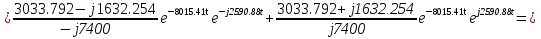 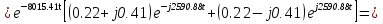 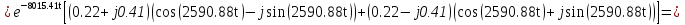 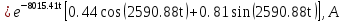 В итоге: 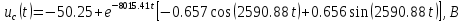 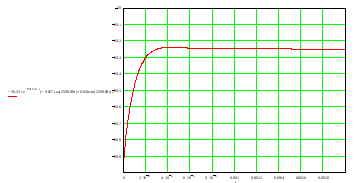 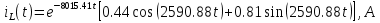  |
