Контрольная 1. Контрольная работа 1 Задача 6
 Скачать 1.85 Mb. Скачать 1.85 Mb.
|
|
Контрольная работа №1 Задача 6. Смесь идеальных газов состоит из 32 кг СО2, 40 кг N2 и 8 кг О2. В начальном состоянии параметры смеси р1 = 0,6 МПа и t = 370ºC. В результате адиабатного расширения давление смеси уменьшается до р2 = 0,1 МПа. Определить объём смеси в начальном и конечном состояниях, температуру и плотность смеси в конечном состоянии, работу расширения и изменение внутренней энергии смеси. Считать, что теплоёмкость газов не зависит от температуры и определяется по таблице 1 приложения. Определить парциальные давления газов, входящих в смесь в конечном состоянии. Изобразить процесс в pv- и Тs-диаграммах. Дано: m(CO2) = 32 кг; m(N2) = 40 кг; m(O2) = 8 кг; р1 = 0,6 МПа; t1 = 370ºC; р2 = 0,1 МПа. Найти: V1 - ? V2 - ? t2 - ? ρ2 - ? A - ? ΔU - ? Решение: 1. Молекулярные массы компонентов газовой смеси: М(CO2) = 44 кг/кмоль; М(N2) = 28 кг/кмоль; М(O2) = 32 кг/кмоль. 2. Газовые постоянные компонентов смеси: R(CO2) = R / М(CO2) = 8,314 / 44 = 0,1890 кДж/(кг·К); R(N2) = R / М(N2) = 8,314 / 28 = 0,2969 кДж/(кг·К); R(О2) = R / М(О2) = 8,314 / 32 = 0,2598 кДж/(кг·К). 3. Масса смеси: mсм = m(CO2) + m(N2) + m(O2) = 32 + 40 + 8 = 80 кг. 4. Массовые доли компонентов: ω(CO2) = m(CO2) / mсм = 32 / 80 = 0,4 ω(N2) = m(N) / mсм = 40 / 80 = 0,5; ω(О2) = m(O2) / mсм = 8 / 80 = 0,1. 5. Газовая постоянная смеси: Rсм = ω(CO2)·R(CO2) + ω(N2)·R(N2) + ω(О2)·R(О2) = = 0,4·0,189 + 0,5·0,2969 + 0,1·0,2598 = 0,25 кДж/(кг·К). 6. Теплоёмкость газов не зависит от температуры и определяется по таблице 1 приложения [1]. Азот и кислород – это двухатомные газы, а углекислый газ – трехатомный. Тогда СрМ(N2) = СрМ(О2) = 29,1 кДж/(кмоль·К); СvМ(N2) = СvМ(О2) = 20,8 кДж/(кмоль·К); СрМ(СО2) = 37,4 кДж/(кмоль·К); СvМ(СО2) = 29,1 кДж/(кмоль·К); Переведем мольные теплоемкости в массовые: Срm(N2) = 29,1 / 28 = 1,0393 кДж/(кг·К); Сvm(N2) = 20,8 / 28 = 0,7429 кДж/(кг·К); Срm(О2) = 29,1 / 32 = 0,9094 кДж/(кг·К); Сvm(О2) = 20,8 / 32 = 0,65 кДж/(кг·К); Срm(СО2) = 37,4 / 44 = 0,85 кДж/(кг·К); Сvm(СО2) = 29,1 / 44 = 0,6614 кДж/(кг·К). 7. Теплоемкость смеси при постоянном давлении и постоянном объеме: Срm см = ω(CO2)·Срm(CO2) + ω(N2)·Срm(N2) + ω(О2)·Срm(О2) = = 0,4·0,85 + 0,5·1,0393 + 0,1·0,9094 = 0,9506 кДж/(кг·К); Сvm см = ω(CO2)·Сvm(CO2) + ω(N2)·Сvm(N2) + ω(О2)·Сvm(О2) = = 0,4·0,6614 + 0,5·0,7429 + 0,1·0,65 = 0,7010 кДж/(кг·К). 8. Показатель адиабаты: k = Срm см / Сvm см = 0,9506 / 0,701 = 1,356. 9. Объём смеси в начальном состоянии: V1 = RсмT1mсм / p1 = 0,25·103·(370 + 273)·80 / 0,6·106 = 21,43 м3. 10. Объём смеси в конечном состоянии после адиабатного расширения: V2 = V1(p1 / p2)1/k = 21,43·(0,6 / 0,1)1/1,356 = 80,33 м3. 11. Температура смеси после расширения: Т2 = Т1(p2 / p1)k-1/k = 643·(0,1 / 0,6)1,356-1/1,356 = 401,7 К. Тогда t2 = T2 – 273 = 401,7 – 273 = 128,7оС. 12. Плотность смеси в конечном состоянии из уравнения Менделеева-Клапейрона: ρ2 = Р2Мсм / RT2 = Р2 / RсмT2 = 0,1·106 / 0,25·103·401,7 = 0,9958 кг/м3. Здесь Мсм = R / Rсм. 13. Изменение внутренней энергии: ΔU = Сvm см(Т2 – Т1)mсм = 0,701·(401,7 – 643)·80 = -13532,1 Дж = -13,53 кДж. 14. Работа процесса расширения: А = -ΔU = 13532,1 Дж = 13,53 кДж. 15. Изобразим адиабатный процесс в pv- и Тs-диаграммах.  Задача 12. Кислород из начального состояния 1 изотермически сжимается до состояния 2, а затем в изохорном процессе охлаждается до состояния 3, в котором p3 = p1. В точке 2 параметры кислорода t2 = 1200ºC и p2 = 6 МПа, в точке 3 температура t3 = 300ºC. Показать процесс 1-2-3 в pv- и Ts-диаграммах. Определить значения p, t и v в точках 1, 2 и 3. Вычислить удельные значения работы, теплоты, изменения внутренней энергии и энтропии кислорода в процессах 1-2, 2-3 и 1-2-3 в целом. Изохорный процесс рассчитать с учётом зависимости теплоёмкости кислорода от температуры (см. табл. 2 приложения). Решение: 1. Запишем уравнение состояния кислорода в виде pv = RT, где p – давление, v – удельный объём, T – абсолютная температура, R = Rμ / μ = 8,314 / 0,032 = 259,8 Дж/(кг·К). Здесь R – газовая постоянная кислорода; Rμ = 8,314 Дж/(моль∙К) – универсальная газовая постоянная; μ = 32∙10-3 кг/моль – молярная масса O2. По условию T1 = T2 = 1200 + 273 = 1473 К; Т3 = 300 + 273 = 573 К; p2 = 6 МПа; p3 = p1. Пользуясь вышеприведенной формулой, определим недостающие параметры состояния в каждой из трёх точек: v2 = v3 = RT2 / р2 = 259,8·1473 / 6·106 = 0,0638 м3/кг; р3 = р1 = RT3 / v3 = 259,8·573 / 0,0638 = 2,3·106 МПа; v1 = RT1 / р1 = 259,8·1473 / 2,3·106 = 0,1664 м3/кг. Процесс 1-2 (изотермический) Количество теплоты q равно работе l: q12 = l12 = RT1 ln(v2 / v1) =259,8·1473·ln(0,0638 / 0,1664) = -3,67·105 Дж/кг. Внутренняя энергия идеального газа в изотермическом процессе не изменяется: Δu12 = 0. Удельное изменение энтропии: Δs12 = q12 / T1 = -3,67·105 / 1473 = -249,15 Дж/(кг·К). Процесс 2-3 (изохорный) В таблице 2 приложения находим средние молярные изохорные теплоемкости кислорода в интервалах температур от 0 до t2 = 1200ºC и от 0 до t3 = 300ºC: С2vμ = 25,32 Дж/(моль·К); С3vμ = 22,09 Дж/(моль·К). Тогда средняя молярная изохорная теплоемкость в процессе 2-3 составит: cvμ ср = (С3vμt3 – С2vμt2) / (t3 – t2) = = (22,09·300 – 25,32·1200) / (300 – 1200) = 26,40 Дж/(моль·К). Средняя удельная изохорная теплоемкость: cv ср = cvμ ср / μ = 26,4 / 0,032 = 825 Дж/(кг·К). Удельное количество теплоты: q23 = cv ср(Т3 – Т2) = 825·(573 – 1473) = -7,425·105 Дж/кг Работа в изохорном процессе равна нулю, то есть l23 = 0. Удельное изменение внутренней энергии Δu23 = q23 – l23 = q23 = -7,425·105 Дж/кг. Удельное изменение энтропии: Δs23 = cv ср ln(Т3 / Т2) = 825·ln(573 / 1473) = -778,94 Дж/(кг·К). Условно примем, что удельная энтропия в точке 3 равна нулю: s3 = 0. Тогда удельные энтропии в точках 2 и 1 составят: s2 = s3 – Δs23 = 0 – (-778,94) = 778,94 Дж/(кг·К); s1 = s2 – Δs12 = 778,94 – (-249,15) = 1028,09 Дж/(кг·К). Характеристики суммарного процесса: q = q12 + q23 = -3,67·105 -7,425·105 = -11,095·105 Дж/кг. l = l12 + l23 = -3,67·105 + 0 = -3,67·105 Дж/кг. Δu = Δu12 + Δu23 = 0 -7,425·105 = -7,425·105 Дж/кг. Δs = Δs12 + Δs23 = -249,15 -778,94 = -1028,09 Дж/(кг·К). Сведем полученные данные в общую таблицу:
Для построения графиков вычислим дополнительно значения параметров состояния в одной промежуточной точке. Процесс 1-2 – изотермический, поэтому, если удельный объем газа равен v, то его давление р равно: р = р1v1 / v. Пусть в точке А v = 0,1 м3/кг, тогда р = 2,3·106·0,1664 / 0,1 = 3,83·106 МПа. 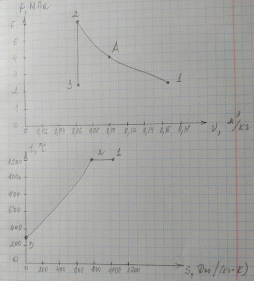 Задача 35. Водяной пар из начального состояния p1 = 2,0 МПа и t1 = 600ºС при постоянном объёме охлаждается до температуры t2 = 300ºС, а затем адиабатно переводится в состояние 3, где его степень сухости х3 = 0,9. Определить параметры пара в состояниях 1, 2 и 3, удельные количество теплоты и работу расширения пара в процессе 1-2-3. Процесс показать в Ts- и hs-диаграммах. Решение: 1. Из h-S диаграммы определяем:  - начальные параметры т. 1 по двум известным параметрам (p1 = 2,0 МПа, t1 = 600ºС): h1 = 3690 кДж/кг; s1 = 7,7 кДж/(кг·К); υ1 = 0,2 м3/кг; u1 = 3290 кДж/кг; - поскольку процесс перегрева пара изохорный, то по двум параметрам пара t2 = 300ºС и υ2 = υ1 = 0,2 м3/кг определим остальные параметры в точке 2: h2 = 3044 кДж/кг; s2 = 7,0 кДж/(кг·К); р2 = 1,28 МПа; u2 = 2788 кДж/кг; - при адиабатном процессе s3 = s2 = 7,0 кДж/(кг·К), х3 = 0,9. Тогда h3 = 2400 кДж/кг; t3 = 75оС; р3 = 0,04 МПа; u3 = 2257 кДж/кг; υ3 = 3,65 м3/кг. 2. Удельное количество теплоты В таблице 2 приложения находим средние молярные изохорные теплоемкости водяного пара в интервалах температур от 0 до t1 = 600ºC и от 0 до t2 = 300ºC: С1vμ = 27,89 Дж/(моль·К); С2vμ = 26,27 Дж/(моль·К). Тогда средняя молярная изохорная теплоемкость в процессе 2-3 составит: cvμ ср = (С2vμt2 – С1vμt1) / (t2 – t1) = = (26,27·300 – 27,89·600) / (300 – 600) = 29,51 Дж/(моль·К). Средняя удельная изохорная теплоемкость: cv ср = cvμ ср / μ = 29,51 / 0,018 = 1639,4 Дж/(кг·К). q12 = cv ср(Т2 – Т1) = 1639,4·(573 – 873) = -4,92·105 Дж/кг = -491,8 кДж/кг. Адиабатный процесс протекает без теплообмена с окружающей средой, поэтому q23 = 0. Теплота суммарного процесса 1-2-3: q = q12 + q23 = -491,8 + 0 = -491,8 кДж/кг. 3. Удельная работа расширения пара Работа в изохорном процессе равна нулю, то есть l12 = 0. Работа в адиабатном процессе l23 = cv ср(Т3 – Т2) = 1639,4·(348 – 573)/1000 = -368,9 кДж/кг. Работа расширения суммарного процесса 1-2-3: l = l12 + l 23 = 0 – 368,9 = -368,9 кДж/кг. 4. Представим процесс в Ts- и hs-диаграммах: 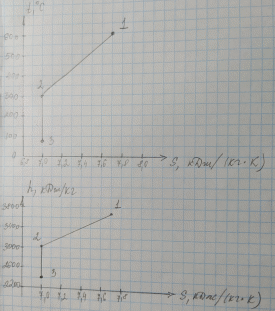 Вопрос 5. Для некоторого газа зависимость истинной теплоёмкости [кДж/(кг·К)] температуры определяется формулой cp = 0,873 + 0,00025t. Найдите значение средней изобарной теплоемкости этого вещества в интервале температур от t1=300ºC до t2 = 500ºC. Ответ: При температуре t2 = 500ºC: cp 2 = 0,873 + 0,00025·500 = 0,998 кДж(кг·К). При температуре t1 = 300ºC: cp 1 = 0,873 + 0,00025·300 = 0,948 кДж(кг·К). Средняя изобарная теплоемкость в данном интервале температур составит: cp ср = (cp2 t2 – cp1 t1) / (t2 – t1) = (0,998·500 – 0,948·300) / (500 – 300) = 1,073 кДж(кг·К). Вопрос 18. Покажите, что в изобарном процессе теплота равна изменению энтальпии, а в изохорном – меньше изменения энтальпии. Ответ: Теплота Q и работа A функциями состояния не являются, они служат формами передачи энергии и связаны с процессом, а не с состоянием системы. При химических реакциях А – это работа против внешнего давления, т.е. в первом приближении А = рV, где V – изменение объема системы (V2 – V1). Так как большинство химических реакций проходит при постоянном давлении, то для изобарно-изотермического процесса (р = const, Т= const) теплота Qp будет равна: Qp = ∆U + p∆V, Qp = (U2 – U1) + p(V2 – V1) Qp = (U2 + pV2) – (U1 + pV1) Сумму U + pV обозначим через Н, тогда Qp = H2 – H1 = ∆H. Величину Н называют энтальпией. Таким образом, теплота при р = const и Т = const приобретает свойство функции состояния и не зависит от пути, по которому протекает процесс. Отсюда теплота реакции Qp в изобарно-изотермическом процессе равна изменению энтальпии системы Н (если единственным видом работы является работа расширения): Qp = ∆H. Нетрудно видеть, что теплота реакции в изохорно-изотермическом процессе (V = const; Т = const), при котором V = 0, равна изменению внутренней энергии системы: Qv = ∆U. Из предыдущих выводов следует: ΔH = ΔU + pΔV ΔH = ΔU + ΔnRT То есть энтальпия отличается от внутренней энергии на величину работы по расширении системы. QP = QV + pΔV QP = QV + ΔnRT. Контрольная работа №2 Задача 6. Влажный воздух на входе в сушильную установку имеет параметры  = 50% и t1= 15ºС. Объёмный расход влажного воздуха на входе V1 = 50 м3/с. Определить количество воды, испаряемой этим воздухом в секунду из высушиваемого материала, если изменение влагосодержания в камере = 50% и t1= 15ºС. Объёмный расход влажного воздуха на входе V1 = 50 м3/с. Определить количество воды, испаряемой этим воздухом в секунду из высушиваемого материала, если изменение влагосодержания в камере d = 20 г на 1 кг сухого воздуха. Задачу решить с использованием Нd-диаграммы. Принять давление В = 0,1 МПа. d = 20 г на 1 кг сухого воздуха. Задачу решить с использованием Нd-диаграммы. Принять давление В = 0,1 МПа.Решение: По Нd-диаграмме по двум известным параметрам 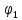 = 50% и t1= 15ºС определяем влагосодержание воздуха = 50% и t1= 15ºС определяем влагосодержание воздухаd1 = 5,5 г/кг сух.возд. При давлении 0,1 МПа и температуре 15оС плотность влажного воздуха ( 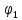 = 50%) равна 1,20 кг/м3. Тогда его удельный объем = 50%) равна 1,20 кг/м3. Тогда его удельный объемv = 1/ρ = 1 / 1,2 = 0,833 м3/кг. Перейдем от объемного расхода к массовому: М = V / v = 50 / 0,833 = 60 кг/с. Конечное влагосодержание определять не нужно, так как по условию сразу задана разность влагосодержаний, то есть Δd = 20 г/кг сух.возд. Тогда количество испаренной воды за секунду составит G = MΔd = 60·20/1000 = 1,2 кг/с. 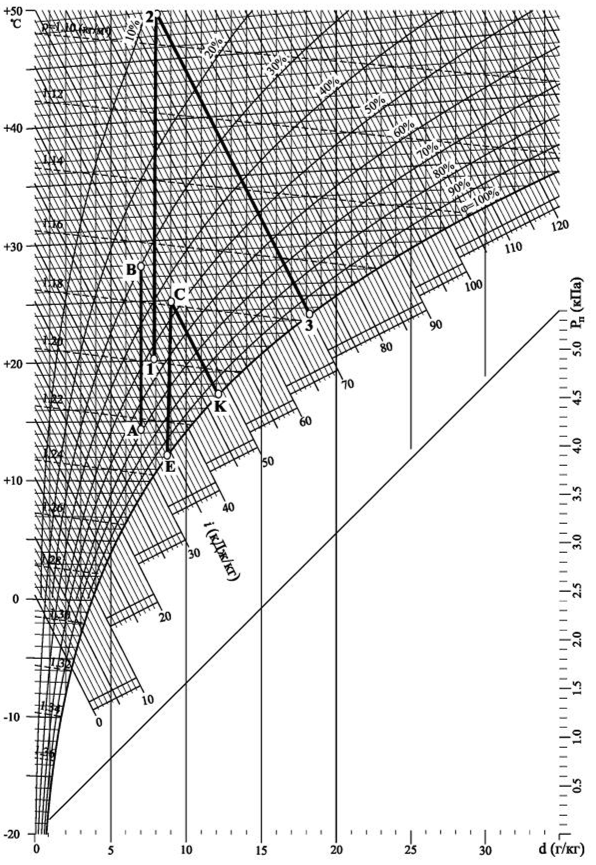 Задача 12. Воздух с начальными параметрами p1 = 12 МПа и t1 = 1000ºC вытекает через сопло во внешнюю среду, давление в которой постоянно и равно 0,1 МПа. Считая воздух идеальным газом с k = 1,34, определить: 1) параметры и скорость воздуха в выходном сечении сужающегося сопла при скоростном коэффициенте  = 0,94; 2) параметры и скорость воздуха в выходном сечении сопла Лаваля на расчётном режиме при = 0,94; 2) параметры и скорость воздуха в выходном сечении сопла Лаваля на расчётном режиме при 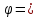 1; 3) площадь минимального сечения сопла Лаваля при расходе воздуха 20 кг/с. 1; 3) площадь минимального сечения сопла Лаваля при расходе воздуха 20 кг/с.Решение: 1. Построим зависимость скорости и расхода потока от отношения давлений 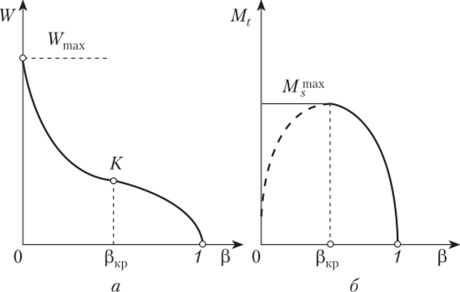 Как следует из рисунка, скорость возрастает во всем диапазоне значений р. При Р = Ркр кривая скорости имеет перегиб. На этом же графике приведена кривая скорости для суживающихся сопел (пунктирная линия). От Р = 1 до Р = Ркр кривые скорости для обоих сопел совпадают. При Р < Ркр кривая скорости для суживающихся сопел параллельна оси абсцисс с ординатой, равной критической скорости. В таких соплах нельзя получить скорости выше критических, поэтому в формулу при Р < Ркр подставляют величину Ркр. Суживающиеся сопла при Р < Ркр применять нецелесообразно, поскольку перепад давлений не может быть использован полностью. 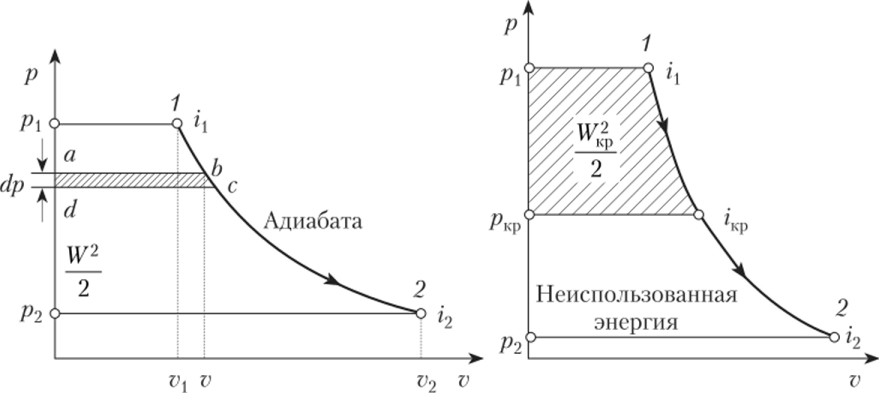 2. В данном задании рабочее тело – воздух, для которого k = 1,34 и βкр= ркр/р1 = 3,77 / 12 = 0,314. Определим соотношение давлений воздуха и среды: рс / р1 = 0,1 / 12 = 0,0083 < βкр = 0,314, следовательно, истечение будет сверхзвуковым. Абсолютная температура на входе в сопло: Т1 = 1000 + 273 = 1273 К. 3. Определение параметров воздуха в выходном сечении сужающегося сопла: а) давление рi = βi·p1 б) температура Ti = T1· 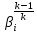 в) скорость потока: ci 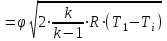 г) удельный объём находится с помощью уравнения состояния идеального газа (уравнение Клапейрона): 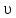 i= i= 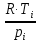 д) плотность (величина, обратная удельному объёму): ρi = 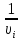 Имеем: ркр = βкр·p1 = 0,314·12 = 3,768 МПа; Tкр = T1· 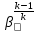 =1273·0,0083(1,34-1)/1,34 = 377,4 К; =1273·0,0083(1,34-1)/1,34 = 377,4 К;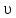 кр = кр = 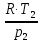 = 287·377,4 / 3768000 = 0,0287 м3/кг; = 287·377,4 / 3768000 = 0,0287 м3/кг; ρкр = 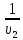 = 1 / 0,0287 = 34,8 кг/м3; = 1 / 0,0287 = 34,8 кг/м3;скр 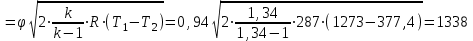 м/с. м/с.4. Определение параметров воздуха в выходном сечении сопла Лаваля: Имеем: р2 = β·p1 = 0,0083·12 = 0,0996 МПа; T2 = T1· 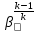 =1273·0,0083(1,34-1)/1,34 = 377,4 К; =1273·0,0083(1,34-1)/1,34 = 377,4 К;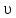 2 = 2 = 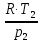 = 287·377,4 / 99600 = 1,0875 м3/кг; = 287·377,4 / 99600 = 1,0875 м3/кг; ρ2 = 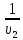 = 1 / 1,087 = 0,92 кг/м3; = 1 / 1,087 = 0,92 кг/м3;с2 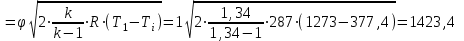 м/с. м/с.5. Площадь минимального критического поперечного сечения сопла: Fкр = 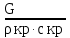 = =  = 0,00043 м2. = 0,00043 м2.Схема сопла Лаваля приведена ниже: 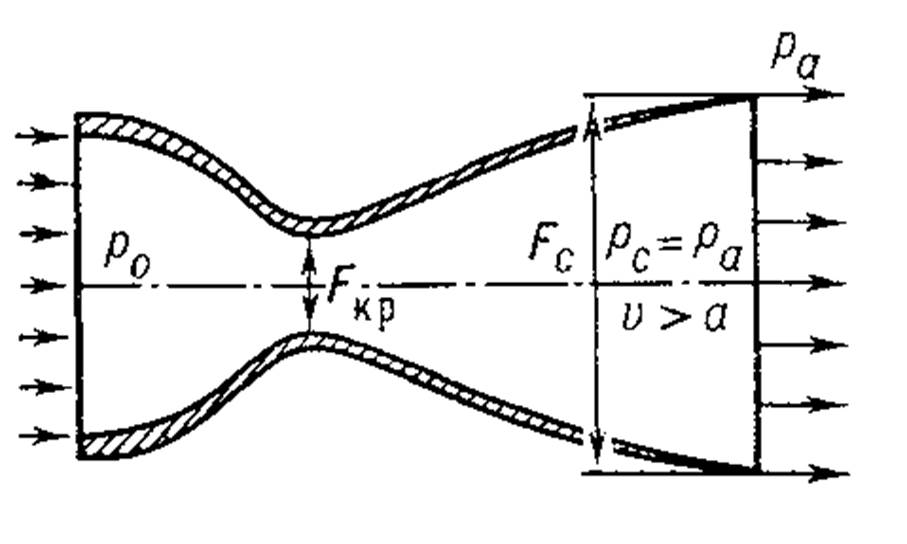 Задача 29. Водяной пар вытекает через сужающее сопло во внешнюю среду, давление в которой постоянно и равно 0,1 МПа. Параметры пара на входе в сопло р1 = 0,5 МПа и t1 = 450ºС. Пренебрегая трением и теплообменом в сопле и приняв для пара ßкр = 0,55, определить параметры пара в выходном сечении, скорость истечения, массовый расход пара и площадь выходного сечения, если объёмный расход пара в выходном сечении V2 = 2,2 м3/с. Какую скорость, температуру и плотность имел бы пар в выходном сечении сопла Лаваля на расчётном режиме при скоростном коэффициенте  = 0,94? = 0,94?Решение: Определим соотношение давлений водяного пара и среды: β = рс/р1 = 0,1 / 0,5 = 0,2 < βкр = 0,55, следовательно, истечение будет сверхзвуковым. Абсолютная температура на входе в сопло: Т1 = 450 + 273 = 723 К. Зная ßкр = 0,55, найдем показатель адиабаты: 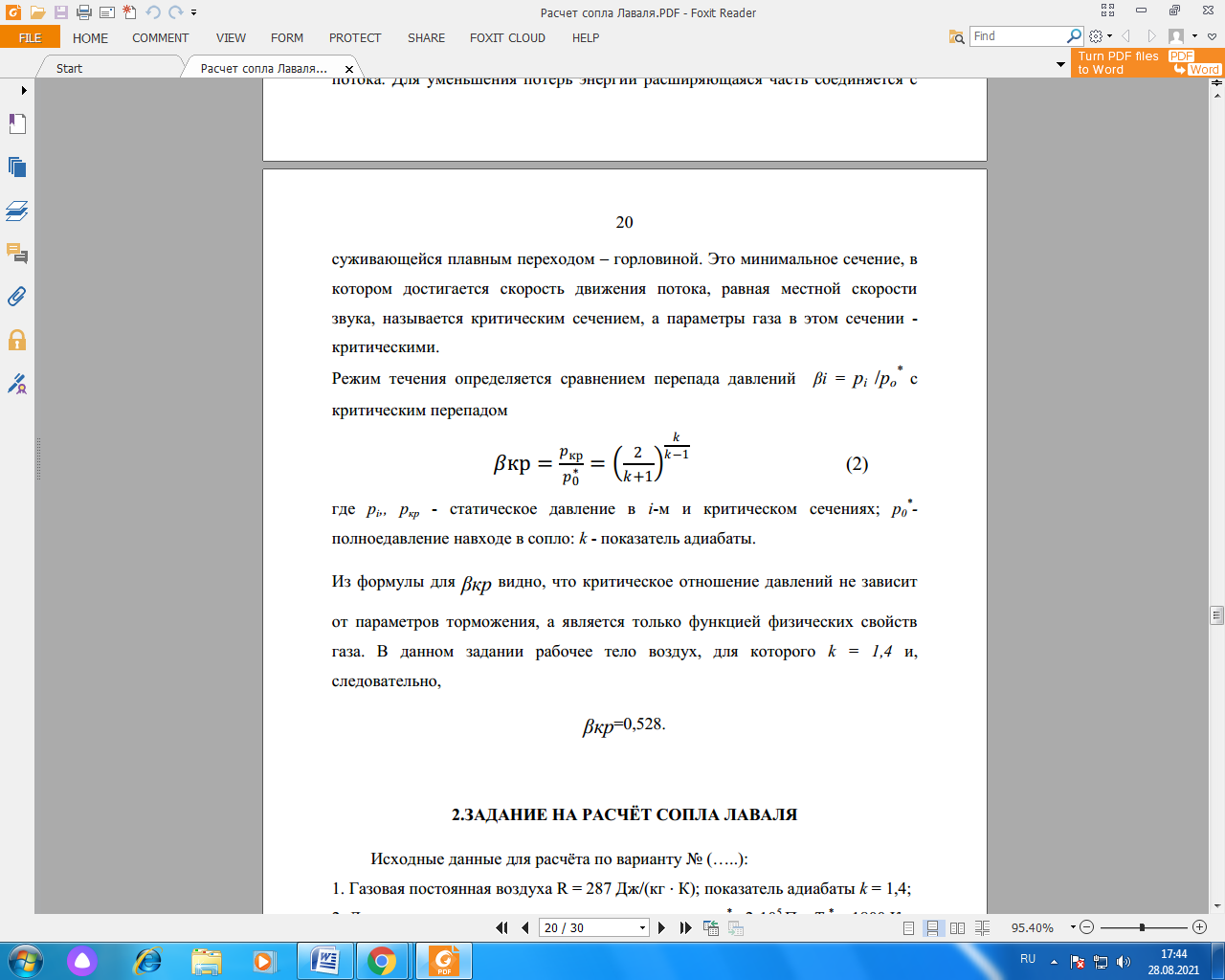 , откуда k = 1,275. , откуда k = 1,275.Определим параметры водяного пара в выходном сечении сопла Лаваля: а) давление рi = βi·p1 б) температура Ti = T1· 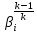 в) скорость потока: ci 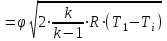 г) удельный объём находится с помощью уравнения состояния идеального газа (уравнение Клапейрона): 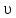 i= i= 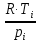 д) плотность (величина, обратная удельному объёму): ρi = 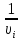 Имеем: р2 = β·p1 = 0,2·0,5 = 0,1 МПа; T2 = T1· 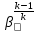 =723·0,2(1,275-1)/1,275 = 511 К; =723·0,2(1,275-1)/1,275 = 511 К;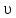 2 = 2 = 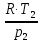 = 287·511 / 100000 = 1,4666 м3/кг; = 287·511 / 100000 = 1,4666 м3/кг; ρ2 = 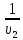 = 1 / 1,4666 = 0,682 кг/м3; = 1 / 1,4666 = 0,682 кг/м3;с2 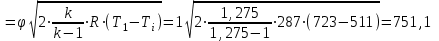 м/с. м/с.Перейдем от объемного расхода к массовому: G = V2 / v2 = 2,2 / 1,4666 = 1,5 кг/с. Площадь поперечного сечения сопла: Fкр =  = =  = 0,00293 м2. = 0,00293 м2.Рассчитаем, какую скорость, температуру и плотность имел бы пар в выходном сечении сопла Лаваля на расчётном режиме при скоростном коэффициенте  = 0,94: = 0,94:сх  м/с. м/с.р2 = β·p1 = 0,2·0,5 = 0,1 МПа; R = 8,314 / 0,018 = 462 Дж/(кг·К); ср = kR/(k-1) = 1,275·462 / (1,275 – 1) = 2142 Дж/(кг·К); T2 = T1· 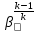 +(1 – +(1 – 2 )сх2 /2ср =723·0,2(1,275-1)/1,275 +(1 – 2 )сх2 /2ср =723·0,2(1,275-1)/1,275 +(1 –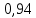 2 )7062 /2·2142 = 524,5 К; 2 )7062 /2·2142 = 524,5 К;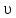 2 = 2 = 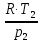 = 462·524,5 / 100000 = 2,4232 м3/кг; = 462·524,5 / 100000 = 2,4232 м3/кг; ρ2 = 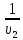 = 1 / 2,4232 = 0,4127 кг/м3. = 1 / 2,4232 = 0,4127 кг/м3.То есть скорость и плотность уменьшились, а температура возросла. Задача 35. Фактическая мощность, затрачиваемая на привод одноступенчатого охлаждаемого компрессора, составляет 43,5 кВт. Определить изотермический к.п.д. этого компрессора, если в нём политропно сжимается 0,2 кг/с азота от давления р1 = 0,1 МПа (t1 = 10ºС) до р2 = 0,7 МПа. Изобразить процесс в координатах p, v и T, s. Решение: 1. Изотермический к.п.д. находится по формуле: ηиз = Nиз / Nфакт, где Nфакт – фактическая мощность, равная по условию 43,5 кВт; Nиз – теоретическое значение мощности при изотермическом сжатии. 2. Азот – двухатомный газ, поэтому для него: Срμ = 29,1 Дж/(моль·К); Сvμ = 20,8 Дж/(моль·К); k = Срμ / Сvμ = 29,1 / 20,8 = 1,4; R = 8,314 / 0,028 = 296,9 Дж/(кг·К). 3. Абсолютная температура перед сжатием Т1 = 10 + 273 = 283 К. 4. Удельный объем газа перед сжатием 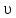 1 = 1 =  = 296,9·283 / 100000 = 0,8402 м3/кг. = 296,9·283 / 100000 = 0,8402 м3/кг.5. Абсолютная температура после сжатия Т2 = Т1 = 283 К. 6. Массовый расход газа М = 0,2 кг/с. 7. Удельный объем газа после сжатия 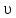 2 = 2 = 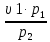 = 0,8402·0,1 / 0,7 = 0,12 м3/кг. = 0,8402·0,1 / 0,7 = 0,12 м3/кг.8. Удельная работа сжатия газа l = RT1·ln(v2/v1) = 296,9·283·ln(0,12 / 0,8402) = -163520,6 Дж/кг. 9. Теоретическая работа привода компрессора: lо = |l| = 163520,6 Дж/кг. 10. Теоретическая мощность привода компрессора: Nт = Nиз = lоМ = 163520,6·0,2 = 32704 Вт = 32,7 кВт. 11. Окончательно изотермический к.п.д. составит ηиз = 32,7 / 43,5 = 0,752 или 75,2 %. 12. Изобразить процесс одноступенчатого сжатия в координатах p,v и T,s:  Задача 48. Рассчитать цикл ГТУс изохорным подводом теплоты, если начальные параметры рабочего тела р1 = 0,1 МПа; t1 = -20ºС, степень повышения давления при сжатии ß = 5, а температура рабочего тела на входе в турбину t3 = 750ºС. Определить параметры в характерных точках цикла, подведённое и отведённое количество теплоты, работу и термический к.п.д. цикла, а также термический к.п.д. цикла Карно в том же интервале температур. Изобразить цикл в координатах p, v и T, s. Решение: Изобразим цикл такой ГТУ в осях p,v и T,s: 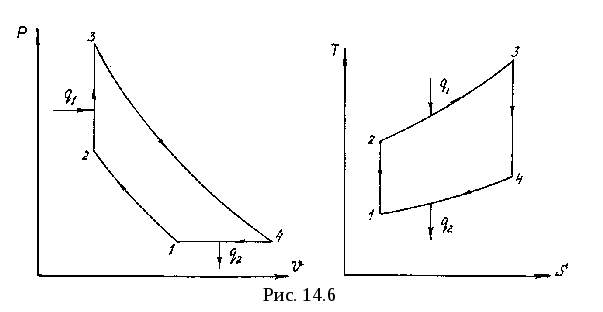 Цикл состоит из следующих процессов: 1-2 – адиабатное сжатие воздуха в компрессоре; 2-3 – подвод теплота q1 к газу при v = const; 3-4 – адиабатное расширение газа в турбине; 4-1 – изобарный отвод тепла q2 от рабочего тела. Параметры цикла: откуда р2 = β·р1 = 5·0,1 = 0,5 МПа. При этом из изобары 4-1: р4 = р1 = 0,1 МПа. Найдем термический к.п.д. цикла. Для этого вначале определим температуры в узловых точках цикла через заданную температуру Т1. Из адиабаты 1-2: 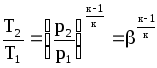 , откуда , откуда T2 = (273 – 20)·5(1,4-1)/1,4 = 400,7 К. Согласно закону Шарля, для изохорного процесса 2-3 справедливо записать: р2/Т2 = р3/Т3, откуда р3 = р2·Т3 / Т2 = 0,5·1023 / 400,7 = 1,2765 МПа. Тогда λ = 1,2765 / 0,5 = 2,553. Из изохоры 2-3: Имеем: Т3 = 2,553·400,7 = 1023 К. Из адиабаты 3-4: 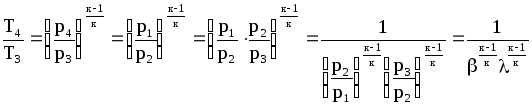 . .Откуда 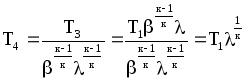 . .Имеем: Т4 = 2,5531/1,4·253 = 494,2 К. Найдем q1 и q2: Тогда 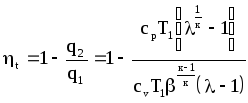 . .Окончательно получим  . . Имеем для рабочего тела (воздуха) при k = 1,4: Срμ = 29,1 Дж/(моль·К) = 29,1 / 0,029 = 1003,4 Дж/(кг·К); Сvμ = 20,8 Дж/(моль·К) = 20,8 / 0,029 = 717,24 Дж/(кг·К); q1 = Сvμ(T3 – T2) = 717,24·(1023 – 400,7)/1000 = 446,34 кДж/кг; q2 = Срμ(T4 – T1) = 1003,4·(494,2 – 253)/1000 = 242,02 кДж/кг; l = q1 – q2 = 446,34 – 242,02 = 204,32. Итого: - из адиабаты 1-2: Т1 = 253 К; р1 = 0,1 МПа; v1 = R·T1/(μ·p1) = 1·8314·253/(29·100000) = 0,725 м3/кг; v2 = v1·(p1 / p2)1/k = 0,725·(0,1 / 0,5)1/1,4 = 0,230 м3/кг; - из изохоры 2-3: Т2 = 400,7 К; р2 = 0,5 МПа; v3 = v2 = 0,230 м3/кг; - из адиабаты 3-4: Т3 = 1023 К; р3 = 1,2765 МПа; v4 = v3·(p3 / p4)1/k = 0,23·(1,2765 / 0,1)1/1,4 = 1,418 м3/кг; - из изобары 4-1: Т4 = 494,2 К; р4 = 0,1 МПа. Термический к.п.д. цикла: ηт = 1 – 242,02 / 446,34 = 0,46. Термический к.п.д. цикла Карно в том же интервале температур: ηк = 1 – Т1 / Т3 = 1 – 253 / 1023 = 0,75. Вопрос 5. Воздух течёт по каналу, имеющему форму сопла Лаваля. Давление воздуха во входном сечении р1 = 0,12 МПа, давление в среде, куда вытекает воздух, рс = 0,1 МПа. Приведите графики изменения скорости и давления воздуха по длине канала. Ответ: 1. Определим соотношение давлений воздуха и среды: рс / р1 = 0,1 / 0,12 = 0,83 > βкр = 0,528, следовательно, истечение будет дозвуковым. 2. Пусть процесс идет при 25оС. Тогда абсолютная температура на входе в сопло: Т1 = 25 + 273 = 298 К. 3. Определение параметров газа по длине сопла: а) давление рi = βi·p1 б) температура Ti = T1· 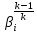 в) скорость потока: ci 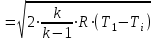 Имеем (принимая, что для воздуха k = 1,4): р2 = β·p1 = 0,83·0,12 = 0,10 МПа; T2 = T1· 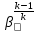 =298·0,83(1,4-1)/1,4 = 282,6 К; =298·0,83(1,4-1)/1,4 = 282,6 К;с2 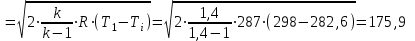 м/с. м/с.Схематично графики изменения скорости и давления воздуха по длине канала будут выглядеть следующим образом: 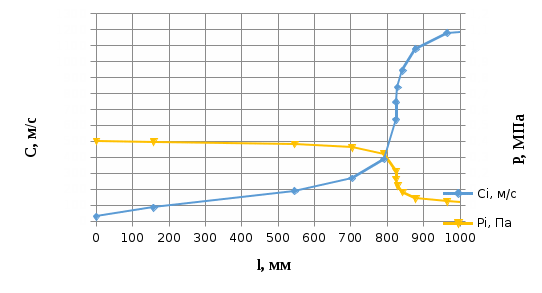 Вопрос 18. Сравните графическим способом термические к.п.д. циклов с изохорным (цикл Карно) и изобарным (цикл Дизеля) подводом теплоты. Степени сжатия и максимальные температуры в циклах одинаковы. Ответ: 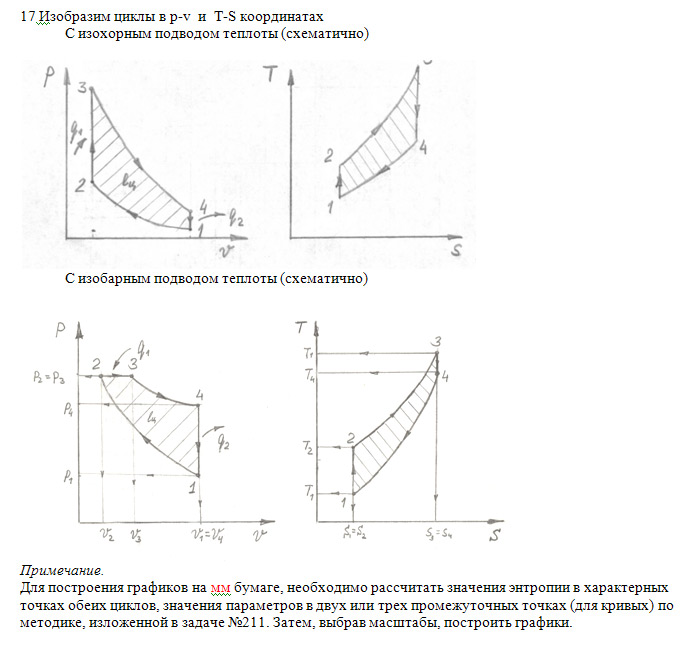 Требования идеального цикла Карно не выполняет ни один из известных циклов (Отто, Дизеля, Ранкина, Стерлинга). Из анализа цикла Карно следует, что КПД термодинамического цикла зависит от разницы между максимальной температурой T1 и минимальной температурой T2. Так как температура T2 может быть в самом крайнем случае температурой окружающей среды, то КПД термодинамического цикла никогда не достигнет 100 %. КПД цикла Дизеля, в условиях одинакового максимально возможного давления, больше, чем КПД цикла Отто. Цикл со смешенным подводом теплоты занимает по эффективности промежуточное положение между циклами Отто и Дизеля как в условиях сравнения при одинаковой степени сжатия ε, так и при сравнении по условию одинакового максимального давления в цилиндре двигателя. Контрольная работа № 3 Задача 6. Паротурбинная установка работает по циклу с регенеративным подогревом питательной воды в смешивающем подогревателе. Параметры пара перед турбиной: р1 = 9 МПа, t1 = 500ºС, давление в конденсаторе р3= 0,004 МПа. Отбор пара для подогрева воды осуществляется при давлении 0,12 МПа. Внутренний относительный к.п.д. ступеней ƞоi = 0,8. Определить расход пара через турбину, если её мощность равна 50 МВт. Изобразить процесс расширения пара в турбине и цикл в координатах h, s и T, s. Решение: Задача 12. Мощность турбины ТЭЦ, работающей по схеме с ухудшенным вакуумом, составляет 30 МВт. Определить расход пара и количество теплоты, направляемое потребителю, если начальные параметры пара р1 = 3,5 МПа, t1 = 435ºС, давление в конденсаторе р2 = 0,12 МПа, а конденсат из него отводится при температуре насыщения. Процесс расширения пара в турбине считать изоэнтропным. Изобразить цикл в координатах h, s и T, s. Решение: Вопрос 5. Покажите графически, как зависит термический к.п.д. цикла ПТУ от давления пара перед турбиной. Какими эффектами сопровождается повышение давления? Приведите конкретный численный пример и изобразите соответствующие циклы в координатах Т, s и h, s. Ответ: Вопрос 18. Какие требования предъявляются к свойствам хладагентов парокомпрессионных холодильных установок с термодинамической точки зрения? Проиллюстрируйте каждое из этих требований изображением циклов в соответствующей системе координат. Ответ: |
