кр. Контрольная работа Неустроева. Контрольная работа 2 По учебной дисциплине Организация обучения математике Вариант Неустроева Анна Александровна
 Скачать 0.54 Mb. Скачать 0.54 Mb.
|
|
Министерство образования и науки Хабаровского края Краевое государственное бюджетное профессиональное образовательное учреждение «Хабаровский педагогический колледж имени Героя Советского Союза Д.Л.Калараша» Контрольная работа №2 По учебной дисциплине «Организация обучения математике» Вариант 7. Выполнила: Неустроева Анна Александровна Курс 2.Группа ПНК-21з Специальность 44.02.02 Преподавание в начальных классах Форма обучения :заочная Проверил: Преподаватель Хорева Галина Владимировна «_____» ____________2019 Оценка-____________________ Хабаровск,2019 Задание 1. « Проверка самостоятельной письменной работы должна носить обучающий характер. Для этого учитель может использовать различные приемы исправления ошибок учащихся: • подчеркнуто выражение, при нахождении значения которого допущена ошибка; • зачеркнут неверный результат; • неверное вычисление зачеркнуто и написан правильный вариант (или дано указание, какие вопросы необходимо повторить); • на полях указан тип выражений, в которых допущена ошибка; • подчеркнута та операция (для письменных вычислений), где допущена ошибка. Расположите эти приемы по степени самостоятельности в исправлении собственных ошибок учащимися. Чем Вы будете руководствоваться при выборе приема исправления ошибок?» Решение: •подчеркнута та операция (для письменных вычислений), где допущена ошибка; •на полях указан тип выражений, в которых допущена ошибка; •подчеркнуто выражение, при нахождении значения которого допущена ошибка; •зачеркнут неверный результат; •неверное вычисление зачеркнуто и написан правильный вариант (или дано указание какие вопросы необходимо повторить); В первую очередь, при выборе приема исправления ошибок, нужно дать возможность учащемуся самостоятельно исправить допущенную ошибку. С помощью самостоятельной работы над ошибками ребенок сможет сам анализировать свои действия по решению какой-то конкретной задачи. При этом у школьников развиваются умения разбираться в задачах, планировать их решение, и прогнозировать результат. С помощью таких приемов ученики смогут обнаруживать, объяснять и исправлять ошибки. Очень важно в работе над ошибками добиться того, чтобы учащиеся стремились избавиться от них. При отсутствии у детей такого стремления не будет успеха в повышении грамотности учащихся. Задание 2.7 « Определите по характеру ошибки её причины. Как предупредить (исправить) эти ошибки?» 64 + 30 = 97; 76 – 20 = 50 Характер ошибки и ее причина: Получение неверного результата вследствие пропуска операций, входящих в прием, или выполнения лишних операций. Обычно такие ошибки возникают в результате невнимательности учеников. Как предупредить: Для предупреждения подобных ошибок необходимо научить и постоянно побуждать учеников выполнять проверку решения примеров. В данном случае используется проверка, основанная на связи между компонентами и результатом действий сложения и вычитания. С этим способом проверки ученики знакомятся в концентре «Сотня». Рассуждать нужно именно так: «Проверю решение примера 64 + 30 = 97: из суммы 97 вычту слагаемое 30 получится 67, но так как первое слагаемое 64 значит, пример решен неверно. Решаю снова». Важно при этом, чтобы ученик сам нашел ошибку: «К четырем единицам я прибавил 3, но это 3 десятка, я их уже прибавил к десяткам». Вычитание проверяется путем сложения разности и вычитаемого, а также с помощью вычитания разности из уменьшаемого. Заметим, что способ проверки путем прикидки результата здесь не подходит: получили сумму 97 которая больше каждого из слагаемых 64 и 30, однако ответ неверен. Это не значит, что им не надо пользоваться, он часто помогает установить, что результат неверен. То же самое делаем и с вычитанием. Пусть ученики сначала выполнят сравнение результата с компонентами, а затем обратятся к другому способу проверки. Задание 3. «Введение алгоритмов сложения и вычитания многозначных чисел можно организовать по-разному: * Переход от развернутой записи в строчку к записи в столбик: 4812+3156=(4000+800+10+2)+(3000+100+50+6)=(4000+3000)+(800+100)+(10+50)+ +(2+6)=7000+900+60+8=7968 * Использование аналогии со способом вычисления двузначных и трехзначных чисел: +58 + 458 +7458 27 127 3127 Какие еще методические приемы введения алгоритмов сложения и вычитания предлагаются в учебниках математики? При ответе сделайте ссылку на соответствующий учебник с указанием его авторов и года издания.» Решение уравнений:  Математика. 4 класс. Учебник в 2 ч. Аргинская И.И., Ивановская Е.И., Кормишина С.Н. c 98 Сложение и вычитание с переходом через разряды:  стр. 47 Математика. 4 класс. Учебн. Для общеобразоват. Учреждений. в 2 ч. Ч.1/[М.И. Моро, М.А. Бантова, Г.В. Бельтюкова и др.]. -8-е изд. – М. : Просвещение, 2011 – 112 с. : ил. – (Школа России). Задание 4. 4.7 « Наиболее трудными для учащихся случаем вычитания многозначных чисел является прием вычитания с переходом через несколько разрядов и прием, при котором в записи уменьшаемого используются нули. Запишите подробное объяснение ученика при нахождении значения разности» Решение: 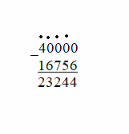 Запишем вычитание в столбик, разряд под разрядом. Вычитаем единицы: из 0 нельзя вычесть ,значит занимаем 1дес., но десятков нет, значит для разряда десятков занимаем 1сотню,но сотен тоже нет, поэтому занимаем 1 тысячу для разряда сотен, но тысяч тоже нет, значит занимаем 10 тысяч для разряда тысяч. Т.к десяток заняли для разряд то единиц то отнимаем: 10-6=4 Вычитаем десятки: один десяток заняли разряду единиц и поэтому от 9дес. отнимаем 5дес. и получаем 4дес. Вычитаем сотни: одну сотню заняли разряду десятков и поэтому от 9 сотен отнимаем 7 сотен и получаем 2 сотни. Вычитаем тысячи: одну тысячу заняли разряду сотен и поэтому от 9 тысяч отнимаем 6 тысяч и получаем 3 тысячи. Вычитаем десятки тысяч: так как один десяток тысяч мы заняли разряду тысяч у нас осталось 3 десятка тысяч и от трех десятков тысяч отнимаем 1 десяток тысяч и получаем 2 дес. тыс. И в ответе получаем: 40000-16756=23244, Задание 5. «Разработайте фрагмент урока по формированию конкретного смысла: 5.5 – 5.7 деления по содержанию; Подберите из учебника задания, выполнение которых способствует усвоению конкретного смысла данного арифметического действия. Укажите авторский коллектив и год издания учебника, на который вы ссылаетесь.» Работа по теме урока. 1. Учитель знакомит детей с действием деления (практическая работа - работа в парах). Затем предлагает решить данную задачу: Мама купила 10 яблок. Учитель:- Положите перед собой столько кругов, сколько яблок купила мама. Работайте, дружно, в паре. (Один ученик работает у доски.) Всем членам семьи она раздала по 2 яблока. Надо узнать, сколько человек получили яблоки. Вопрос: - По сколько яблок получит каждый член семьи? (По 2.) Учитель:- Возьмём 2 кружка, отодвинем в сторону. Их получил первый член семьи. - Ещё 2 кружка - второй... и т.д. - На сколько групп разделились кружки? (На 5) - Значит, сколько человек получили яблоки? (5 человек) - Такие задачи, в которых надо по одинаковому количеству раздать, разложить, разделить и узнать, сколько раз, например, по 2 яблока содержится в 10, решают с помощью арифметического действия, которое называется делением. - Решение данной задачи можно записать так: 10 : 2 = 5 - Две точки - это знак деления. Читают данное равенство так: 10 разделить на 2, получится 5. Учитель: - Ребята, а теперь давайте откроем учебник на странице 74 и решим несколько задач:  Математика. 2 класс. В 2 ч. Дорофеев Г.В., Миракова Т.Н., Бука Т.Б. Задание 6. «Выделите последовательность изучения случаев внетабличного умножения и деления в пределах 100 и первой тысячи в учебниках математики (на выбор). Заполните таблицу»
Задание 7. «Объясните, почему при делении одного и того же числа на однозначное число, в одном случае получили шестизначное число, а в другом пятизначное: 327675 : 3 = 109225 327675 : 5 = 65535 Запишите подробное объяснение ученика при нахождении значения первого частного.» В первом случае в частном получили 6 цифр, так как первое неполное делимое было из разряда сотен тысяч. 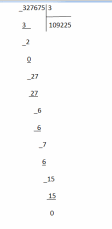 Во втором случае в частном получили 5 цифр, так как первое неполное делимое было из разряда десятков тысяч. 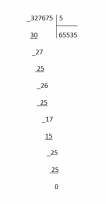 Записываем делимое 327675 и делитель 3: 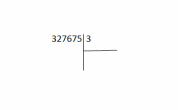 Деление начинаем с высшего разряда. В числе 327675 3 сот.тыс. Сотни тысяч- шестой разряд в записи числа ,значит количество цифр в записи частного будет 6. 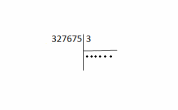 Образуем первое неполное делимое .Найдем первую цифру в записи частного. 3сот. тыс. можно разделить на три и получить сотни тысяч. В частном записываем 1. 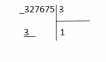 Умножим: 3*1=3 Вычтем: 3-3=0 – Сотни тысяч разделились все. Делим десятки тысяч. 2 дес. тыс. – второе неполное делимое Десятков тысяч 2, но 2 дес. Тыс. нельзя разделить на 3, так чтобы в частном получились десятки тысяч. Ставлю в частном 0. 0 – столько десятков тысяч будет в частном Делим единицы тысяч. 27 тыс. – это третье неполное делимое. 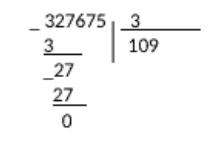 Разделим: 27/3=9 – столько единиц тысяч будет в частном Умножим: 9*3=27. Вычтем: 27-27=0 – единицы тысяч разделились все. Делим сотни: 6 сот. – это четвертое неполное делимое Разделим: 6/3=2; Умножим: 2*3=6; Вычтем: 6-6=0 – сотни разделились полностью. 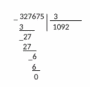 Делим десятки: 7 – это пятое неполное делимое; Разделим: 7/3=2; Умножим: 3*2=6; Вычтем: 7-6=1 – столько десятков остается разделить. Сравним остаток с делителем: десятков осталось меньше 3. 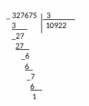 Делим единицы: 1 дес. 5 ед, всего 15 ед – это шестое неполное делимое. Разделим: 15/3=5; Умножим: 5*3=15; Вычтем: 15-15=0; В остатке поучается 0. Число разделилось нацело, без остатка. 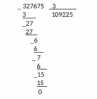 Читаем ответ: Значение частного 327675 и 3=числу 109225 Задание 8 «Запишите подробное объяснение ученика при нахождении значения произведения: 8.7 160 · 270» Решение: Запишем первый множитель 160,второй множитель 270(трехзначное число).Числа записываю друг под другом, единицы под единицами, десятки под десятками, сотни под сотнями): 160 *270 Единицами обоих множителей являются нули, на них мы пока обращать внимания не будем, а перейдем пока к умножению десятков и сотен. Умножим первый множитель на десятки второго множителя, на 7 и получаем 112-это первое неполное произведение. Результат записываем под десятками: 160 *270 112 Умножение не закончено. Умножаем первый множитель на сотни второго множителя, на 2 сотни и получаем 32-второе неполное произведение. Результат записываем со сдвигом на один разряд влево т.е под сотнями: 160 *270 112 32 Теперь между первым и вторым неполными произведениями ставим знак «+» и складываем их. 160 *270 112 32 432 Нули просто дописываем к числу 432: 160 *270 112 32 43200 Читаю ответ: значение произведения = числу 43200. Задание 9. «При знакомстве учащихся со случаем умножения с единицей один учитель организовал деятельность детей так: 1.Замените умножение сложением и найдите значение выражения: 1 · 5 . 2.Переставьте множители и найдите результат, используя переместительное свойство умножения: 1 · 5 = 5 · 1 = 5 3.Далее составлялись пары выражений: 1 · 6 = 6 1 · 8 = 8 1 · 12 = 12 6 · 1 = 6 8 · 1 = 8 12 · 1 = 12 Был сделан вывод: при умножении единицы на число и числа на 1 получается это же число. Другой учитель организовал деятельность детей иначе: 1.Сегодня мы познакомимся с особым случаем умножения на число 1 Мы не можем в данном случае заменить произведения суммой и получить результат. Нужно запомнить, что при умножении на единицу мы получаем то число, которое умножаем. 2.Самостоятельно найдите значения произведений: 1 · 6, 1 · 8, 1 · 12 3.Сравните равенства: 1 · 6 = 6 1 · 8 = 8 1 · 12 = 12 6 · 1 = 6 8 · 1 = 8 12 · 1 = 12 Какое свойство выполняется для случая умножения с единицей? Какой организации обучения детей умножению с единицей Вы отдаете предпочтение (считаете грамотной)? Почему?» В данном случае применяется свойство единицы при умножении: «При умножении числа на единицу, получается то же число» При выборе организации обучения детей я отдаю предпочтение организации обучения детей, которую предложил второй учитель, потому что в этом случае педагог использует современный урок, при котором у ученика будет максимум возможностей для самостоятельного приобретения знаний и способностей их применять. Такая организация работы при решении задач способствует формированию универсальных учебных действий. В данном случае учитель подводит учеников к тому что применяется свойство единицы при умножении:«При умножении числа на единицу, получается то же число». Задание 10. «Подберите занимательные задания и игры, с помощью которых будете закреплять навыки табличного умножения и деления.» Живая математика. У учащихся карточки с цифрами от 0 до 9. Учитель читает выражение (3 • 2). Выходит, встает или поднимает руку тот ученик, у кого карточка с цифрой 6. (Можно давать выражения на деление. Если в ответе двузначное число, встают двое учащихся.) Делится - не делится. Учитель называет различные числа, а ученики поднимают руку, если число делится, например, на 3 (на 4, на 5) без остатка. День и ночь. Когда учитель произносит слово «Ночь», учащиеся кладут голову на парту и закрывают глаза. В это время учитель читает (записывает) выражение для устного счета на деление или умножение. Следует небольшая пауза. Затем учитель говорит: «День». Дети открывают глаза, садятся прямо, и те, кто сосчитал, поднимают руку и говорят ответ. (Игра ценна тем, что дает возможность сосредоточиться при счете детям с замедленной реакцией, приучает их воспринимать задание не только по записи, но и на слух.) Составь слово. На доске записаны выражения. Выходят две команды. По сигналу каждый из вызванных решает одно из выражений и выбирает среди подготовленных карточек карточку с числом, соответствующим ответу выражения (на обороте карточки написана буква). Команда, первая составившая слово, например «молодцы», побеждает. Лучший счетчик. На доске записаны выражения: справа и слева их количество одинаковое: 9 • 9, 3 • 8, 7 • 8, 9 • 4, 4 • 8, 9 • 3, 6 • 7, 7 • 3. По команде учащиеся начинают записывать или выкладывать из разрезных цифр соответствующие ответы, один - слева, другой - справа. Выигрывает тот, кто первым справится с заданием. (Проводя эту игру, нужно чаще повторять те случаи умножения и деления, которые труднее запоминаются. Учитель фиксирует ошибки, затем записывает их на заранее подготовленных лентах.) Проверь себя. Для игры нужны карточки, на которых записаны результаты умножения каких-либо чисел, например 18. Учитель показывает карточку, а учащиеся должны записать выражение с таким ответом. «Магазин» На полках выставлены различные игрушки. Вместо таблички с ценой записан пример на карточке. Цены станут известны тогда, когда дети-покупатели «покупая» игрушку, решат записанный пример «Молчание» Ученик должен отвечать на вопросы учителя, не говоря ни слова, а показывая только карточку с числами. Вопросы учителя связаны с изучением таблицы умножения и деления. Такую игру полезно проводить, когда ученики возбуждены и им трудно сосредоточиться без помощи учителя. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
