математика кр3и 4. Контрольная работа 3 07 Линия задана уравнением r r() в полярной системе координат. Требуется
 Скачать 389.63 Kb. Скачать 389.63 Kb.
|
|
Контрольная работа № 3 3.07 Линия задана уравнением r = r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от  равного нулю и увеличивая затем значения равного нулю и увеличивая затем значения  на на 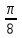 ; ;2) найти уравнение данной линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; 3) по полученному уравнению определить тип линии. 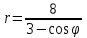
Сделаем чертёж.  Найдем уравнение данной линии в декартовой прямоугольной системе координат 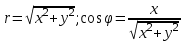 Подставим это значение в уравнение линии:  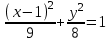 –это уравнение данной линии в декартовой системе координат. –это уравнение данной линии в декартовой системе координат.3)Эта линия является эллипсом, с центром в точке (1,0). 3.17. Для заданной функции найти точки разрыва, если они существуют, и построить график. 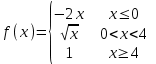 Данная функция определена для всех значений х 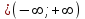 и на каждом из участков задания (-∞,0], (-0,4), [4, +∞) является элементарной и, следовательно, непрерывной. Непрерывность функции может нарушиться лишь в точках, где изменяется ее аналитическое значение, то есть в точках х=4 и х=0. Исследуем эти точки на непрерывность, находя односторонние пределы: и на каждом из участков задания (-∞,0], (-0,4), [4, +∞) является элементарной и, следовательно, непрерывной. Непрерывность функции может нарушиться лишь в точках, где изменяется ее аналитическое значение, то есть в точках х=4 и х=0. Исследуем эти точки на непрерывность, находя односторонние пределы:    4   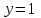  0 При х=0  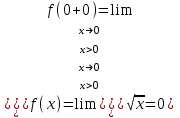 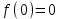  В точке х=0 f(0-0) =f(0+0)= f(0), значит х=0 точка непрерывности. При х=4 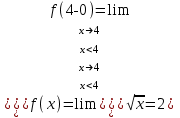 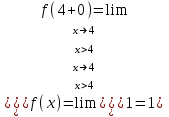  В точке х=4 f(4-0) 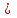 f(4+0), значит х=4 точка разрыва. Т.к. правый и левый пределы конечны, то это точка разрыва первого рода. f(4+0), значит х=4 точка разрыва. Т.к. правый и левый пределы конечны, то это точка разрыва первого рода.Построим схематический график.  3.27 Найти производные функций. 1) 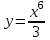 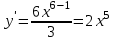 2) 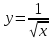 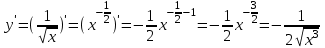 3)  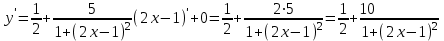 4) 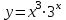  5) 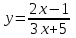  3.37 Найти производные функций. 1) 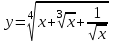 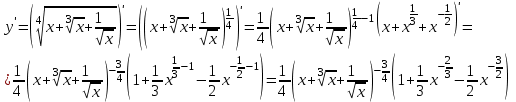 2) 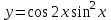 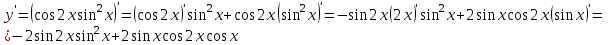 3) 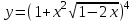 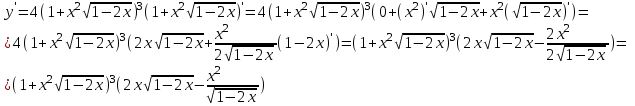 4) 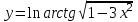 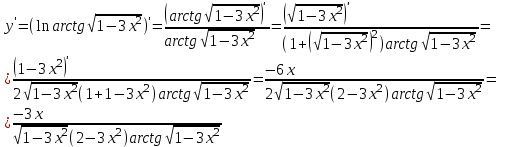 5) 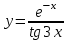 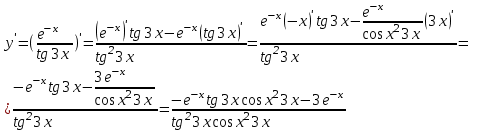 6) 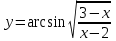 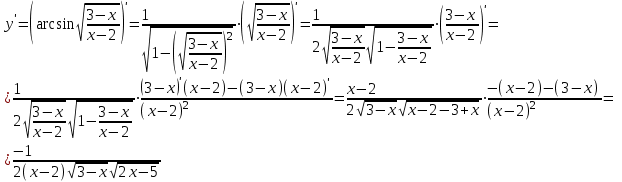 3.47 Найти производные функций 1) 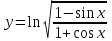 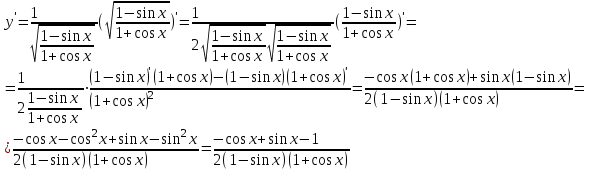 2) 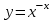 Прологарифмируем обе части уравнения 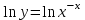 и преобразуем равенство и преобразуем равенство 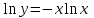 . Пропотенцируем обе части равенства . Пропотенцируем обе части равенства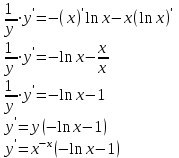 3) 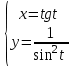  4)  Дифференцируем обе части равенства, учитывая, что у есть функция от х, получим  3.57 Найти пределы функций 1) 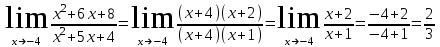 2)  3) 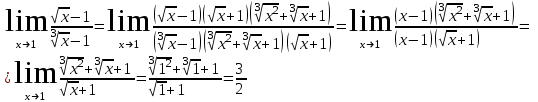 4) 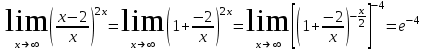 5) 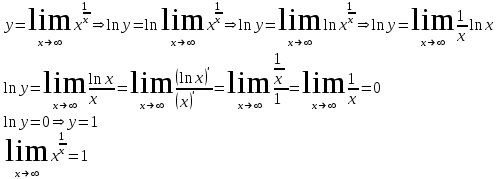 3.67 Найти экстремумы и промежутки монотонности функций; построить графики функций  Область определения функции все числа. Определим критические точки. Для этого найдем производную y'. 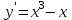 . Тогда y' = 0 или . Тогда y' = 0 или 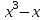 =0 имеет решение при х=-1, х=0, х=1. =0 имеет решение при х=-1, х=0, х=1.Определим знак первой производной на интервалах. y'(x)    – + – +  -1 0 1 -1 0 1 Значит, на промежутках (-,-1),(0;1)– функция возрастает, на промежутках (-;-1) (0 ;1)– функция убывает. Значит, при х=0– максимум, у(0)=5, при х=-1 и х=1– минимум, у(-1)=у(1)=4,75. Определим точки перегиба. Для этого найдем вторую производную y'' функции: 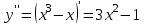 ; ;тогда y'' = 0– имеет решение при х= 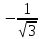 и при х= и при х=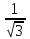 . Получим, что это перегибы. . Получим, что это перегибы.Определим знак второй производной на интервалах. y'' (x)    + – + + – +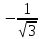 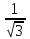 Таким образом, при x (-; 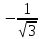 ), ( ), (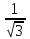 ;+) график функции вогнутый , при x ( ;+) график функции вогнутый , при x ( 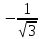 , , 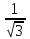 ) –выпуклый. ) –выпуклый.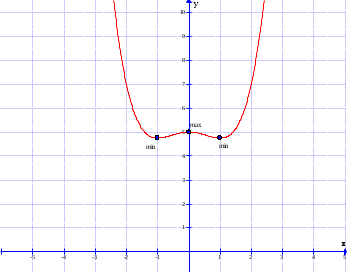 3.77 Исследовать функции методами дифференциального исчисления и построить их графики 1) 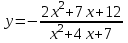 Найдем область определения D(y). Очевидно D(y) = (–;+). Исследуем функцию на непрерывность. 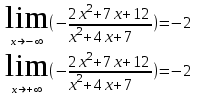 Значит, y=-2 – горизонтальная асимптота. 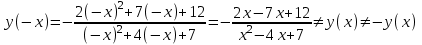 . Функция не является ни четной, ни нечетной. . Функция не является ни четной, ни нечетной.Определим критические точки. Для этого найдем производную y'. 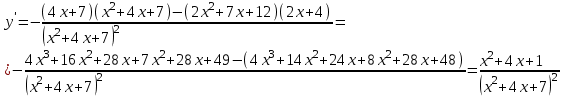 . . Тогда y' = 0 или 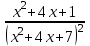 =0 имеет решение при х= =0 имеет решение при х=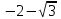 и х= и х=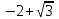 . Определим знак первой производной на интервалах. . Определим знак первой производной на интервалах.y'(x) 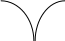   – + – – + –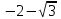 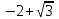 Значит, на промежутках ( 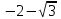 ; ;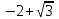 ) функция возрастает, на промежутках (-; ) функция возрастает, на промежутках (-;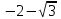 ), ( ), (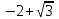 ,+ )– функция убывает. Значит, при х= ,+ )– функция убывает. Значит, при х=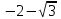 – минимум, у( – минимум, у(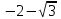 )=-2,29, при х= )=-2,29, при х=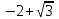 – максимум, – максимум, у( 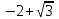 )=-1,712. )=-1,712.Определим точки перегиба. Для этого найдем вторую производную y'' функции:  ; тогда y'' = 0 или ; тогда y'' = 0 или  =0– имеет решение при х=-5, х=-2, х=1. Получим, что это перегибы. =0– имеет решение при х=-5, х=-2, х=1. Получим, что это перегибы. Определим знак второй производной на области определения.    y''(x) y''(x) – + – +  -5 -2 1 Таким образом, при x (-;-5), (-2;1) график функции выпуклый, при x (-5;-2), (1;+ ) график функции вогнутый. Выясним, имеет ли функция вертикальные асимптоты y=kx+b. 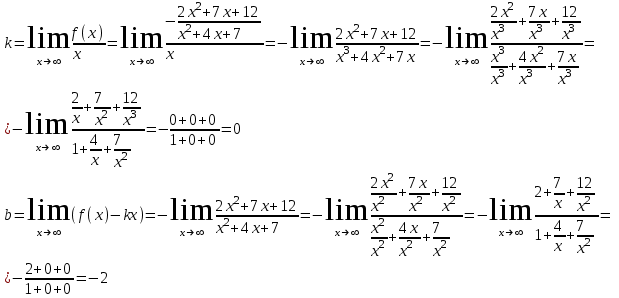 у=-2–горизонтальная асимптота. у=-2–горизонтальная асимптота.7) По результатам исследования строим график функции: 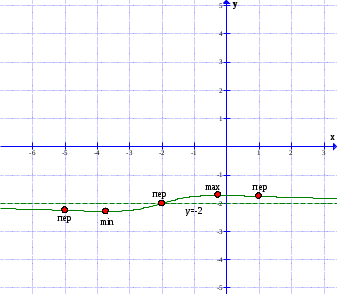 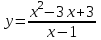 Найдем область определения D(y). Очевидно D(y) = (–;1), (1;+). Исследуем функцию на непрерывность при х=1. 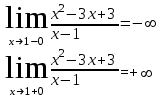 Значит, х=1 – вертикальная асимптота. 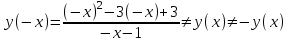 . Функция не является ни четной, ни нечетной. . Функция не является ни четной, ни нечетной.Определим критические точки. Для этого найдем производную y'. 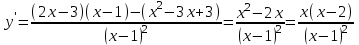 . Тогда y' = 0 или . Тогда y' = 0 или 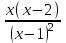 =0 имеет решение при х=0 и х=2. Определим знак первой производной на интервалах. =0 имеет решение при х=0 и х=2. Определим знак первой производной на интервалах.y'(x)     + – – + + – – +0 1 2 Значит, на промежутках (0;1),(1; 2) функция убывает, на промежутках (-;0), (2,+ )– функция возрастает. Значит, при х=2 – минимум, у(2)=1, при х=0 – максимум, у(0)=-3. Определим точки перегиба. Для этого найдем вторую производную y'' функции:  ; тогда y'' = 0 или ; тогда y'' = 0 или  =0– не имеет решения. Получим, что перегибов нет. =0– не имеет решения. Получим, что перегибов нет. Определим знак второй производной на области определения.  y''(x) y''(x) + –  1 Таким образом, при x (-;1) график функции выпуклый, при x (1;+ ) график функции вогнутый. Выясним, имеет ли функция вертикальные асимптоты y=kx+b.  у=х-2–наклонная асимптота. у=х-2–наклонная асимптота.7) По результатам исследования строим график функции: 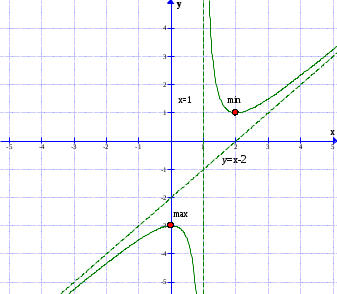 3.87 Определить количество действительных корней уравнения 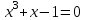 , найти их приближенное значение с точностью до 0,001. , найти их приближенное значение с точностью до 0,001.Вычислим производную: 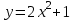 Знак второй производной всегда положительный, значит, функция всегда возрастает и пересекает ось Ох один раз. Значит, имеется только один действительный корень. Искомый корень находится в интервале (0,1). Тогда f(0)= 03+0-1= -1<0, f(1)= 13+1-1=1>0 . Т.к. f(0)*f(1)<0 и 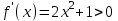 в любой точке, то условия теоремы выполняются, значит, на отрезке [0,1] находится единственный корень этого уравнения. в любой точке, то условия теоремы выполняются, значит, на отрезке [0,1] находится единственный корень этого уравнения.1)  и вычислим f(с)= 0,53+0,5-1=-0,375<0. и вычислим f(с)= 0,53+0,5-1=-0,375<0. f(b)*f(с)<0, значит, принимаем а1=с=0,5, b1=b=1. Переходим к отрезку [а1, b1]= [0,5,1]. 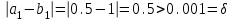 2) 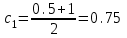 и вычислим и вычислим f(0,75)=0,753+0,75-1= 0,17>0. f(а1)*f(с1)<0, значит, принимаем а2=а1= 0,5, b2=с= 0,75. Переходим к отрезку [а2, b2]= [0,5;0,75]. 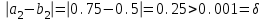 3) 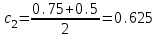 и вычислим и вычислим f(0,625)=0.6253+0,625-1=-0,13<0. f(b2)*f(с2)<0, значит, принимаем а3=c2=0,625, b3=b2=0,75. Переходим к отрезку [а3, b3]= [0,625;0,75]. 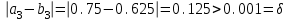 4) 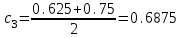 и вычислим и вычислим f(0,6875)=0.68753+0,6875-1= 0,0125<0. f(а3)*f(с3)<0, значит, принимаем а4=b3=0,625, b4=c3=0,6875. Переходим к отрезку [а4, b4]= [0.625;0,6875].  5)  и вычислим и вычислим f(0,66875)=0.668753+0,66875-1= -0,03<0. f(b4)*f(с4)<0, значит, принимаем а5=c4=0,66875, b5=b4=0,6875. Переходим к отрезку [а5, b5]= [0,66875;0,6875]. 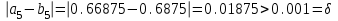 6) 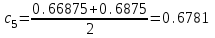 и вычислим и вычислим f(0,6781)=0.67813+0,6781-1= -0,0101<0. f(b5)*f(с5)<0, значит, принимаем а6=c5=0,6781, b6=b5=0,6875. Переходим к отрезку [а6, b6]= [0,6781,0,6875]. 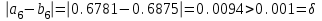 7) 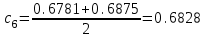 и вычислим и вычислим f(0,6828)=0.68283+0,6828-1= 0,0011>0. f(a6)*f(с6)<0, значит, принимаем а7=a7=0,6781, b7=c6=0,6828. Переходим к отрезку [а7, b7]= [0,6781;0,6828]. 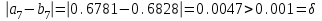 8) 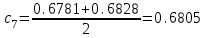 и вычислим и вычислим f(0,6805)=0.68053+0,6805-1= -0,0044<0. f(b7)*f(с7)<0, значит, принимаем а8=c7=0,6805, b8=b7=0,6828. Переходим к отрезку [а8, b8]= [0,6805;0,6828]. 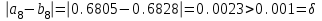 9) 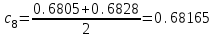 и вычислим и вычислим f(0,68165)=0.681653+0,68165-1= -0,0016<0. f(b8)*f(с8)<0, значит, принимаем а9=c8=0,68165, b9=b8=0,6828. Переходим к отрезку [а9, b9]= [0,68165;0,6828]. 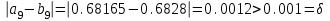 10)  и вычислим и вычислим f(0,68223)=0.682233+0,68223-1= -0,0002<0. f(b9)*f(с9)<0, значит, принимаем а10=c9=0,68223, b10=b9=0,6828. Переходим к отрезку [а10, b10]= [0,68223;0,6828]. 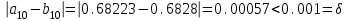 Значит, можно принять  за приближённое значение корня. за приближённое значение корня.Контрольная работа № 4 4.07Найти неопределенный интеграл. Результаты проверить дифференцированием. А)  Проверим результат дифференцированием: 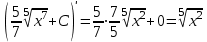 Б) 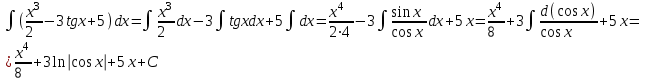 Проверим результат дифференцированием:  В) 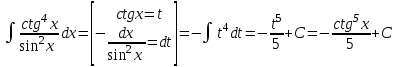 Проверим результат дифференцированием: 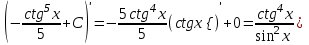 4.17 Найти неопределенные интегралы. А)  Б) 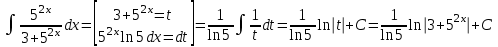 4.27 Найти неопределенные интегралы. А)  Б) 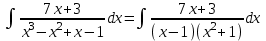 Разобьем дробь на слагаемые:   4.37 Найти неопределенные интегралы. А) 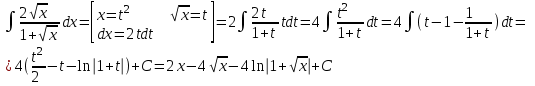 Б) 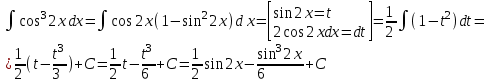 4.47 Вычислить определенные интегралы. А) 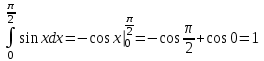 Б) 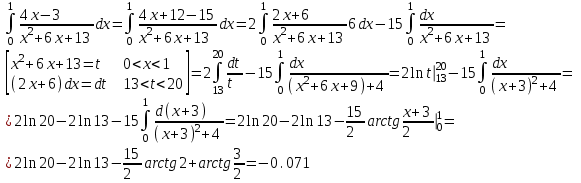 4.57 Вычислить площади фигуры, ограниченных линиями А) 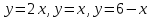 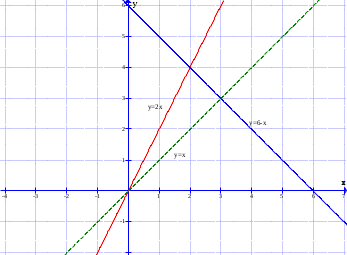 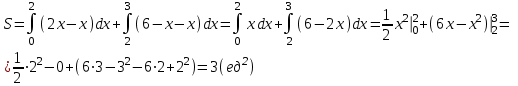 Б) 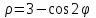 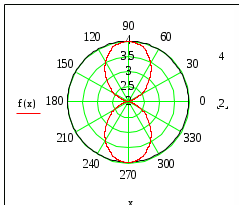 Площадь вычисляется по формуле:  . .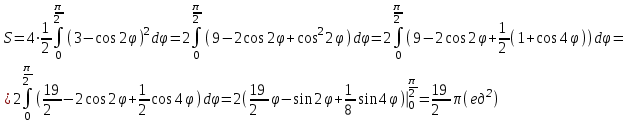 4.67 Вычислить значение определенного интеграла с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака  Воспользуемся формулой Симпсона 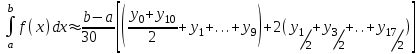 Разобьём на 10 интервалов :
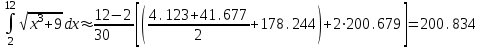 4.77 Проверить сходимость несобственных интегралов. 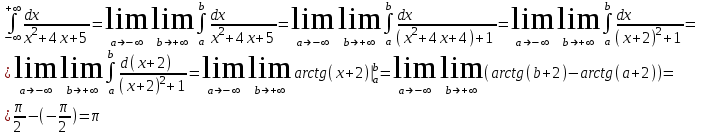 Несобственный интеграл сходится. |
