Электрические машины. Кр. Контрольная работа по дисциплине "Электрические машины" Вариант 48 студент группы элэт32 Кудинов И. А

• Название: Контрольная работа по дисциплине "Электрические машины" Вариант 48 студент группы элэт32 Кудинов И. А
• Анкор: Электрические машины
• Дата: 05.12.2021
• Размер: 288.09 Kb.
• Имя файла: Кр.docx
• Тип: Контрольная работа; #292182

Балаковский инженерно-технологический институт - филиал

федерального государственного автономного образовательного учреждения

высшего образования

«Национальный исследовательский ядерный университет «МИФИ»

Факультет атомной энергетики и технологий

Кафедра Атомной энергетики

КОНТРОЛЬНАЯ РАБОТА

по дисциплине

“Электрические машины”

Вариант 48

Выполнил: студент группы: ЭЛЭТ-32

Кудинов И.А.

«___»______________202___г.

Проверил: к.т.н. доц. каф. АТЭ

Губатенко М.С.

«___»______________202___г.

Балаково 2021

Задача 1. Для трехфазного трансформатора мощностью S_ном = 400 кВ∙А, соединение обмоток Y/Y₀ – 0, известно: номинальное напряжение на зажимах первичной обмотки трансформатора U_{1 ном} = 10000 В, напряжение на зажимах вторичной обмотки в режиме холостого хода U₂₀ = 690 В, напряжение короткого замыкания u_к = 4,5 %, мощность коротко замыкания Р_К = 5500 Вт, мощность холостого хода Р₀ = 1080 Вт, ток холостого хода i₀ = 3,2 %.

Определить: 1) сопротивление обмоток трансформатора R₁, X₁, R₂, X₂; 2) сопротивление намагничивающей цепи Z₀ и его составляющие R₀ и X₀, которыми заменяется магнитная цепь трансформатора; 3) угол магнитных потерь δ.

Построить характеристики трансформатора: 1) зависимость U₂ = f(β) напряжения от нагрузки (внешняя характеристика); 2) зависимость η = f(β) коэффициента полезного действия от нагрузки; β – коэффициент нагрузки трансформатора (коэффициент мощности нагрузки принять cos φ₂ = 0,75).

Построить векторную диаграмму трансформатора при нагрузке, составляющей 0,8 от номинальной мощности трансформатора S_ном и cos φ₂

= 0,75). Составить Т-образную схему замещения трансформатора.

Решение.

1. 
   Полная паспортная мощность трансформатора S_ном соответствует вторичной обмотке. Так как КПД трансформатора близок к 100 %, то значение S_ном близко к мощности его первичной обмотки. Для трехфазного трансформатора S_ном = 3 ∙U_1ном I_1ном, где U_1ном и I_1ном номинальные значения напряжения и тока первичной обмотки. Отсюда
   

^I1ном <sup>

S</sup>ном

_ 400 1000 Вт _{ 23,09 А .}

3  10000 В

По условию ток холостого хода i₀ = 3,2 %, тогда фактическое значение I₀ = 0,032∙23,09 А = 0,74 А.

Мощность потерь холостого хода Р₀ = 3 ∙U_1ном I₀∙cosφ₀,

где φ₀ – сдвиг фаз между током и напряжением в первичной обмотке, откуда

P
cos₀ ⁰

_ 1080 Вт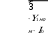

3  10000 B 0,73 A

^{ 0,086 , а угол φ}0 ^{= arcos (0,086) = 85,07°.}

Угол магнитных потерь δ = 90° - φ₀ ≈ 90° - 85° = 5°.

Напряжение короткого замыкания u_к = 4,5 % от U_1ном, где U_1ном - линейное значение напряжения. По условию трансформатор включен по схеме Y/Y₀, тогда действующее значение линейного напряжения короткого замыкания U_К = 0,045∙10000 В = 450 В, а значение фазного напряжения

короткого замыкания

^UКФ

 ^UК  259,8 В .

Ток короткого замыкания I_К соответствует номинальному значению I_1ном. При соединении в звезду линейный ток равен фазному, поэтому I_К = I_КФ = I_{1 ном} = 23,09 А.

Коэффициент трансформации трансформатора



k  ^U1НОМ  ^{10000 В} 15

^U20

690 В

2.Расчет сопротивлений схемы замещения трансформатора

Полное сопротивление короткого замыкания фазы

К
_Z ^U КФ

^IКФ

 ^{259,8 В}  11,3 Ом .

23,07 А

Мощность потерь короткого замыкания P_К = 3∙(I_К)²∙R_К, откуда

активное сопротивление короткого замыкания

R_К 

P_К


К
3  I²

_ 5500

3  23²

 3,5 Ом .

Индуктивная составляющая сопротивления короткого замыкания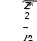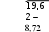

Х_К  ,8 Ом.



По найденным значениям сопротивлений короткого замыкания можно определить синус и косинус угла сдвига фаз между током и напряжением в режиме КЗ:

Z



К
сos ^RК

К

_ 3,5

11,3

 0,3 ^и

sin  ^XКК

 ^10,8  0,9

11,3

Z

К
Активное сопротивление первичной обмотки

R  (R )^  ^RК  ^{3,5 Ом}  1,75 Ом.



1 2 _{2 2}

Индуктивное сопротивление первичной обмотки

X  (X )^  ^XК  ^{10,8 Ом}  5,4 Ом. Активное сопротивление вторичной обмотки

R  ^R2  ^{1,75 Ом} 0,0078Ом.

² _k2

225

Индуктивное сопротивление первичной обмотки

Х  ^Х2  ^{5,4 Ом} 0,024 Ом.

² _k2

225

Сопротивления намагничивающей цепи:

- полное

_{Z } ^U1НОМФ _


0
^I0Ф

10000В

3  0,74 А

 4504Ом ;

- активное

R₀ 

P₀

3  I²

_ 1080 Вт

3  (0,74 А)²

 657 Ом ;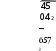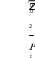

- индуктивное Х₀  

4456 Ом .

Расчет КПД трансформатора. КПД трансформатора


К
_{ }  S_НОМ соs_{2 ,}

  S

НОМ

 соs₂

• 
  P₀
  

  ²  P

где β – коэффициент нагрузки трансформатора. Так как параметры S_НОМ, P₀, P_К и cosφ₂ являются постоянными, КПД является функцией только одной переменной β, то есть η = f(β). Задаваясь набором дискретных значений β (0,01; 0,025; 0,05; 0,1; 0,2; 0.3; 0,5; 0.6; 0,7; 0,8; 0,9; 1,0) можно

вычислить соответствующие значения η. Результаты расчета занесем в табл. 3.

Коэффициент нагрузки имеет максимальное значение, которое вычисляется по паспортным значениям для мощностей потерь P₀ и P_К: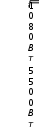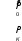

_max  

 0,2

и тогда η_max = η(β_max) = 0,969.

4.Расчет потери напряжения и параметров внешней характеристики. При изменении коэффициента нагрузки напряжение на вторичной обмотке изменяется:

Δu₂ = β∙(u_ка∙cos φ₂ + u_кр∙sin φ₂),

где u_ка и u_кр – активная и реактивная составляющие напряжения короткого замыкания u_к, выраженные в процентах или относительных единицах, причем u_ка = u_к∙cos φ_к, а u_кр = u_к∙sin φ_к. Подставляя вычисленные ранее значения, получим u_ка = 4,5∙0,3 = 1,35 и u_кр = 4,5∙0,9 = 4,05. Так как u_к, cos φ_к и cosφ₂ величины постоянные, то зависимость Δu₂ = f(β) является линейной: Δu₂(β) = k∙β, где k =(u_ка∙cos φ₂ + u_кр∙sin φ₂) = 1,35∙ 0,75 + 4,05∙ 0,66

= 3,686 (%). В итоге Δu₂ = 3,686 ∙β, u₂ = 100%-Δu₂ = 100% - 3,686 ∙β, а

абсолютное значение U₂ = u₂∙U₂₀. Зависимость линейна, ее можно построить по двум точкам, но для последующих расчетов значения u₂ и U₂ вычисляются для выбранного выше набора дискретных значений β и заносятся в табл. 3.

Таблица 3

Результаты расчета КПД и напряжения на вторичной обмотке

Пара- метр	Коэффициент нагрузки трансформатора β
β	0,01	0,025	0,05	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1,0
η	0,555	0,757	0,904	0,924	0,956	0,965	0,967	0,969	0,967	0,966	0,964	0,963	0,962
Δu2, %	-	-	-	0,507	1,014	1,521	2,028	2,535	3,042	3,549	4,056	4,563	5,070
U2, В	-	-	-	397,97	395,94	393,92	391,89	389,86	387,83	385,80	383,78	381,75	379,72

Построение векторной диаграммы

По условию векторную диаграмму требуется построить для коэффициента нагрузки β = 0,8 и коэффициента мощности нагрузки cos φ₂

= 0,75. Векторная диаграмма строится для одной фазы, поэтому все величины должны быть рассчитаны для фазных значений.

Из таблицы 3 для заданных параметров линейное напряжение

U₂(0,8) = 383,78 В, тогда фазное

^U2ф

_ ^U2 л

 ^383,78  221,8 В.

3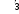

Приведенное значение вторичного напряжения


2ф 2ф
U^′ = U ∙k = 221,8 B ∙15 = 3327,6 B.

Вектор тока I_2ф отстает по фазе от вектора напряжения U_2ф на заданный угол φ₂ и для β = 0,8 имеет значение I₂ = 0,8∙I_2ном, где I_2ном вычисляется через полную паспортную мощность S_н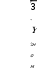ом:

^I2ном <sup>

S</sup>ном

 ^{400 1000}  578,03 А.

1,73 400

Тогда I_2ф(0,8) = 0,8∙578,03 = 462,4 А, а приведенное значение тока I′_2ф =

^I2ф  ^462,4  30,8

А. Сдвиг фаз между приведенными значениями тока и

k 15

напряжения I′_2ф и U′_2ф остается неизменным, то есть φ₂. Построение векторной диаграммы удобно начать с векторов I′_2ф, U′_2ф и угла φ₂.

Рекомендуется выполнять следующие подготовительные операции и требования:

• 
  изображать диаграмму по размерам страницы или на отдельном листе миллиметровой бумаги;
  
• 
  выбрать масштаб для векторов исходя из размеров листа и значений параметров;
  
• 
  внимательно рассмотреть взаимное расположение векторов на типовой векторной диаграмме и по возможности придерживаться того же расположения. Обратить внимание на то, что векторы U′_2ф, Е₁ и Е′₂ ориентируются вниз под небольшим углом (ориентация может быть совершенно произвольной).
  

С учетом замечаний начинают выполнять диаграмму с вектора U′_2ф, который направляется от середины листа вниз. Под углом φ₂ к вектору U′_2ф строится вектор тока I′_2ф, который отстает от напряжения и сдвинут по фазе по часовой стрелке.

Вектор ЭДС Е′₂ строится на основе уравнения электрического состояния вторичной обмотки:

Е′₂ = U′_2ф + I′_2ф∙r′₂ + jI′_2ф∙X′₂,

где модуль произведения I′_2ф∙r′₂ = 30,8 А ∙4,35 Ом = 134,1 В;

а I′_2ф∙X′₂ = 30,8 А ∙8,95 Ом = 275,7 В.

Вектор I′_2ф∙r′₂ есть напряжение на активном сопротивлении, по фазе совпадает с направлением тока I′_2ф. Изобразим его на векторной диаграмме, совмещая начало с концом вектора U′_2ф. Вектор jI′_2ф∙X′₂ есть напряжение на индуктивном сопротивлении, оно опережает напряжение I′_2ф∙r′₂ на угол 90°. Изобразим его, совмещая начало с концом вектора I′_2ф∙r′₂ с поворотом на 90° против часовой стрелки.

Примечание. Для наглядности рисунок выполнен с нарушением пропорций напряжений относительно общего масштаба.

Фрагмент векторной диаграммы для описанной части на рис. 1.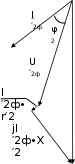

^E′2
Рис. 1. Фрагмент векторной диаграммы

Вектор магнитного потока Ф_m по закону электромагнитной индукции всегда опережает наведенную им ЭДС Е′₂ и Е₁ на угол 90°. Изобразим его из начала векторной диаграммы с поворотом против часовой стрелки в произвольном масштабе. Ток холостого хода I₀ опережает магнитный поток на угол потерь δ = 5°. После его построения на основе уравнения

намагничивающих токов (I_1ф = I₀ - I′_2ф) можно изобразить вектор тока первичной обмотки I_1ф.

Вектор напряжения первичной обмотки U₁ строится на основе уравнения электрического состояния первичной обмотки:

U₁ = - E₁ + I_1ф∙r₁ + jI_1ф∙X₁,

где произведение I_1ф∙r₁ есть падение напряжения на активном сопротивлении первичной обмотки, а I_1ф∙X₁ на ее индуктивном сопротивлении.

В этих произведениях неизвестен ток I_1ф, соответствующий току I_2ф при β = 0,8. Его можно определить по масштабу на векторной диаграмме или пренебречь током I₀ в уравнении намагничивающих токов и принять, что I_1ф = I′_2ф = 30,8 А. Тогда I_1ф∙r₁ = I′_2ф∙r′₂ =134,1 В, а I_1ф∙X₁ = I′_2ф∙Х′₂ = 275,7 В.

Построение векторов уравнения U₁ = - E₁ + I_1ф∙r₁ + jI_1ф∙X₁ аналогично построению векторов по уравнению электрического состояния вторичной обмотки. При этом необходимо учесть условие, что Е₁ = Е′₂ и что вектор E₁ по направлению противоположен вектору - E₁.

В итоге векторная диаграмма в целом будет соответствовать рис. 3, а схема замещения рис. 2.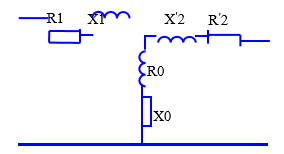



Рис. 2. Схема замещения трансформатора

Задача 2. Номинальная мощность трехфазного асинхронного двигателя с короткозамкнутым ротором Р_ном = 40 кВт, номинальное напряжение U_ном = 380 В, номинальный КПД η_ном = 0,925 и номинальный коэффициент мощности cos φ_ном = 0,92. Кратность пускового тока I _пуск/I_ном = 7,0.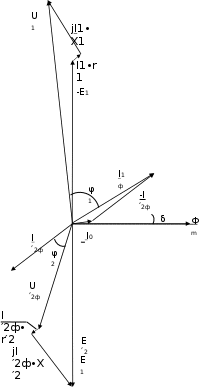




^{Рис. 3. Векторная диаграмма трансформатора для β = 0,8 и соs φ}2 ^{= 0,75}

Определить: 1) потребляемую мощность; 2) номинальный и

максимальный (критический) вращающие моменты; 3) пусковой ток; 4) номинальное и критическое скольжения. Построить механические характеристики М = f(S) и n = f(M).

Решение.

1. 
   Расчет потребляемой мощности
   

КПД двигателя

_{ } ^Рмех _

^Рэл

^Рном _,

^Р1ном

где Р_мех = Р_ном – полезная механическая мощность на валу двигателя, Р_эл = Р_{1 ном} – потребляемая из сети электрическая мощность.

Следовательно, потребляемая мощность

^Р1ном

_ ^Рном _



40

0,93

 43,2

кВт.

2. Расчет номинального и максимального моментов

Номинальный момент

n

ном
М  9550  ^Рном  9550 

ном

40

1420
 269,2 Н∙м.

Перегрузочная способность по максимальному моменту

_{ } ^М max _,

^Mном

где M_max и M_ном – максимальный и номинальный моменты соответственно, откуда

М_max = λ∙M_ном = 2,0 ∙ 269,2 = 538,4 Н∙м.

3. Расчет номинального и пускового токов

Номинальная мощность двигателя

^Р1 ном ^{= 3 ∙U}ном ^{∙ I}ном ^{·cos φ}ном^,

следовательно,

^Iном <sup>

P</sup>1ном

_ 43,2 1000 3  380  0,92
 71,3 А.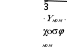

С учетом кратности пускового тока I_пуск = 6,5∙I_ном = 6,5∙71,3 = 463,7 А.

4. Расчет номинального и критического скольжения

По определению, скольжение

_{S } n₁  n_{2 ,}

n₁

где n₁ – частота вращения магнитного поля статора, n₂ - частота вращения ротора.

Для номинального режима n₂ = n_ном = 1420 об/мин, частота вращения магнитного поля n₁ может составлять только 1500 об/мин и тогда:

_{S } n₁  n_{ном } 1500 1420 _{ 0,053}

или 5,3 %.

n
ном

1

1500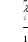

Критическое скольжение: S_кр = S_ном∙(λ+

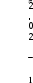) = 0,053∙(2,0 +

) = 0,198

5. Построение механической характеристики

В практических задачах механическую характеристику М = f(S) строят на основе уравнения Клосса:

_{M } 2  M_{max } 2  M_{max .}

^Sкр S

• 
  
  

S ^Sкр

0,198 _

S

S

0,198

Построение графика можно выполнить в программе Matchad по аналитическому выражению или построить по точкам. Во втором случае скольжению S задается набор значений в интервале от 0 до 1 и одновременно для каждого значения S вычисляется частота вращения n₂. Результаты расчетов заносятся в табл. 4. Построение механических характеристик в программе Matchad приведено на рис. 4 и 5. Для корректной работы программы Matchad диапазон изменения переменных и аналитические выражения должны быть приведены выше и левее поля графиков.

Таблица 4

Точки механической характеристики двигателя

Парамет

Номер точки

р	1	2	3	4	5	6	7	8	9	10	11	12
S	0,05 3	0,1	0,17 5	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1,0
n,об/мин	1420	1350	1238	1200	1050	900	750	600	450	300	150	0
M, Н∙м	67,3	104, 3	121, 0	120, 5	105, 3	88, 8	75, 5	65, 2	57, 0	50, 5	45, 5	41, 2

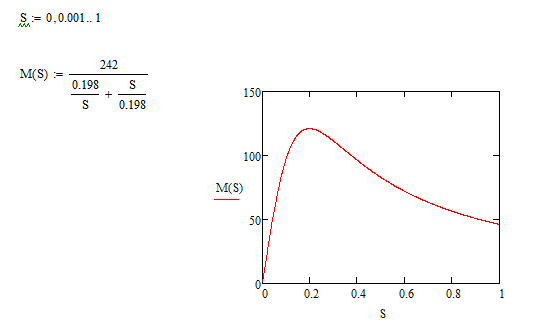Рис. 4. Механическая характеристика двигателя М = f(S), построенная в программе Matchad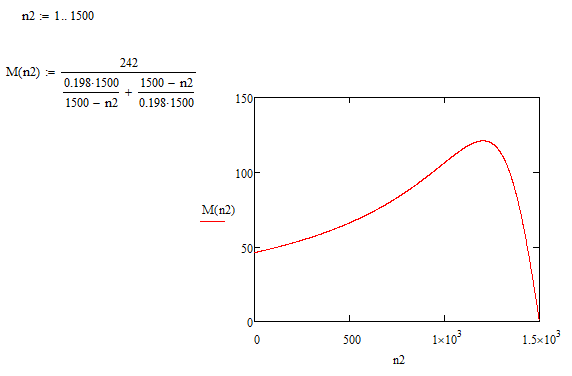



^{Рис. 5. Механическая характеристика двигателя n}2 ^{= f(M),} построенная в программе Match