Координаты вектора. Координаты вектора
 Скачать 0.52 Mb. Скачать 0.52 Mb.
|
|
Координаты вектора. В пространстве введем декартову систему координат. Определим векторы  такие, что Х(1,0,0), У(0,1,0), Z(0,0,1). Свободные векторы, представителями которых являются векторы такие, что Х(1,0,0), У(0,1,0), Z(0,0,1). Свободные векторы, представителями которых являются векторы  обозначим обозначим  . Данные векторы некомпланарны, а, следовательно, образуют базис пространства. Все дальнейшие рассуждения будем проводить в этом базисе. . Данные векторы некомпланарны, а, следовательно, образуют базис пространства. Все дальнейшие рассуждения будем проводить в этом базисе.Рисунок  Базис 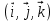 является ортонормированным базисом. является ортонормированным базисом.Определение. Пусть точка М – произвольная точка пространства. Тогда вектор  называется радиус-вектором точки М. называется радиус-вектором точки М.Напомним определение координат вектора в фиксированном базисе. Определение. Упорядоченная тройка чисел (α, β, γ) в разложении вектора  по базису по базису   ) называется координатой вектора ) называется координатой вектора  в базисе в базисе 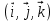 . .Свойства координат вектора. Если векторы  имеют в данном базисе координаты имеют в данном базисе координаты  и и  , то вектор их суммы будет иметь координаты , то вектор их суммы будет иметь координаты . .Заметим, что данное утверждение верно для любого базиса, не только для ортонормированного. Доказательство.  Если вектор 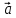 имеет в данном базисе координаты имеет в данном базисе координаты  и α – некоторое вещественное число, то вектор α и α – некоторое вещественное число, то вектор α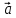 имеет координаты имеет координаты  . .Заметим, что данное утверждение верно для любого базиса, не только для ортонормированного. Доказательство провести самостоятельно, аналогично первому свойству. Пусть точка М имеет в декартовой системе координат следующие координаты: М(х,у,z). Тогда её координаты равны координатам её радиус-вектора в ортонормированном базисе   ), ),  . .Доказательство.    Координаты вектора  равны разности координат конца и начала. равны разности координат конца и начала.(В школе это утверждение берётся за определение координат вектора) Доказательство.  Пусть вектор 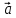 имеет в ортонормированном базисе координаты имеет в ортонормированном базисе координаты  . Тогда длина вектора . Тогда длина вектора 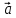 вычисляется по формуле: вычисляется по формуле:| 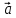 | = | =  . .Для доказательства данного свойства возьмите представителя данного вектора с началом в точке О и воспользуйтесь формулой длины отрезка. Определение. Говорят, что точка С делит отрезок АВ в отношении  , если выполнено равенство , если выполнено равенство . . Заметим, что это определение обобщает уже известное нам определение. Если точка С делит отрезок АВ в отношении  и и А(хА, уА, zА), В(хВ, уВ, zВ), С(хС, уС, zС), то верны равенства хС =  , уС = , уС =  , zС = , zС =  Данное свойство непосредственно следует из свойств 2) и 4). Определение.  Проекцией вектора  на ось х называется число prx на ось х называется число prx , равное , равноеprx  Проекцией свободного вектора на ось x называется проекция его представителя на эту ось. Данное определение корректно, т.е. не зависит от выбора представителя. Аналогично определяем проекцию вектора на ось у и ось z. Задача. Докажите, что проекция вектора 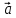 на ось х равна произведению его длины и косинуса угла между вектором на ось х равна произведению его длины и косинуса угла между вектором 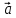 и вектором и вектором  . .Свойство 7. Пусть в пространстве введена декартова система координат и зафиксирован ортонормированный базис   ). Тогда координатами произвольного вектора являются его проекции на координатные оси, т.е. ). Тогда координатами произвольного вектора являются его проекции на координатные оси, т.е.  prx prx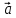 , pry , pry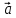 , prz , prz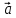 ). ).Доказательство.   Итог. Координаты вектора в декартовой системе координат с введенным ортонормированным базисом   ) можно находить тремя способами: ) можно находить тремя способами:как коэффициенты в разложении данного вектора по базису; как разности координат конца и начала данного вектора; как проекции данного вектора на координатные оси. |
