Курсовая работа По дисциплине Основы построения телекоммуникационных систем и сетей Вариант 07 Содержание
 Скачать 3.38 Mb.
|
|
Studlancer.net - закажи реферат, курсовую, диплом! Курсовая работа По дисциплине: Основы построения телекоммуникационных систем и сетей Вариант 07 Содержание Введение 1. Методы регистрации 1.1 Регистрация посылок методом стробирования 1.2 Интегральный метод регистрации 1.3 Сравнение методов регистрации 1.3.1 Задача №1 2.Синхронизация в системах ПДС 2.1 Устройства синхронизации с добавлением и вычитанием импульсов 2.2 Параметры системы синхронизации с добавлением и вычитанием импульсов 2.3 Расчет параметров системы синхронизации с добавлением и вычитанием импульсов 2.3.1 Задача № 2 2.3.2 Задача № 3 2.3.3 Задача № 4 3. Корректирующее кодирование в системах ПДС 3.1 Циклические коды 3.2 Построение кодера и декодера 3.2.1 Задача № 5 4.Системы ПДС с обратной связью 4.1 Системы с информационной обратной связью 4.2 Системы с решающей обратной связью 4.2.1 Задача № 6 4.2.2 Задача №7 Список литературы Введение Теория передачи дискретных сообщений представляет наиболее разработанную часть общей теории связи. Основной проблемой этой теории является отыскание методов передачи и приема, обеспечивающих получение требуемой верности принятого сообщения, повышение скорости передачи и понижение ее стоимости. Эти задачи нельзя рассматривать в отрыве друг от друга. Действительно, каждую из них можно было бы решать за счет остальных. Так, например, можно легко повысить верность принятого сообщения, уменьшая скорость передачи, либо увеличивая мощность сигнала и т. д. Поэтому только учет всех указанных факторов позволяет правильно сформулировать задачу оптимального построения системы связи. В зависимости от конкретных условий постановка этой задачи различна. В одних случаях требуется обеспечить наибольшую экономичность (или наименьшую затрачиваемую мощность) при заданных верности и скорости передачи. В других случаях заданными являются скорость передачи и мощность сигнала и требуется обеспечить максимальную верность и т. д. Такие задачи постоянно возникают перед инженерами. проектирующими и эксплуатирующими различные системы и линии передачи сообщении, а также разрабатывающими соответствующую аппаратуру. Для их решения необходимо четкое знание теории, позволяющей находить оптимальные (или близкие к ним) условия путем сравнительно простых расчетов, не прибегая к дорогостоящим экспериментам. 1. Методы регистрации Сигнал, поступающий с выхода полунепрерывного канала или КПТ, должен быть отождествлен с “1” или “0”. Процесс определения и запоминания значащей позиции сигнала данных – называется регистрацией. Наиболее распространены для регистрации методы стробирования и интегрирования. дискретный сообщение стробирование синхронизация 1.1 Регистрация посылок методом стробирования Метод стробирования – значащая позиция принимаемого элемента определяются на основании анализа знака импульса в середине единичного интервала.  Если индивидуальное КИ не превышает  , то элемент регистрируются правильно.Говорят идеальная исправляющая способность 50%. Исправляющая способность – это величина, на которую допускаются смещения ЗМ, не вызывающее неправильный прием элемента.  Схема состоит из входного устройства, двух ключей и RS-триггера. Входное устройство имеет два выхода на один транслируется входной сигнал без изменений, а на другой с инверсией (точки 1 и 2). Стробирующие импульсы открывают ключи на время своего существования. Через ключи высокий потенциал поступает на один из входов тригера и переводит его в соответствующее состояние. Последовательность 4 – устанавливает триггер в “1”, а 5 – сбрасывает триггер в “0”. 1.2 Интегральный метод регистрации Решение о виде принятого элемента выносится на основании анализа напряжения на всем единичном интервале.  В идеальном случае (если единичный. элемент не искажен), то Uвых= 1 решением о “1” принимается при  ;решением о “0” принимается при  .В цифровом виде интегральный метод может быть реализован на основе многократного стробирования.  Структурная схема интегрального метода. На ключ поступают стробирущие импульсы. Управление ключом производится сигналом с выхода порогового устройства. Импульсы прошедшие ключ подсчитываются счетчиком. По приходу тактового импульса решающее устройство считывает показание счетчика, сравнивает его с пороговым значением и принимает решение о значащей позиции на текущем интервале. Алгоритм принятия решения: Пусть за время неискаженной токовой посылки появляется N тактовых импульсов, тогда: если показание счетчика   +1 – решение “1” если меньше, то “0” Временные диаграммы работы данной схемы приведены на следующем рисунке  1.3 Сравнение методов регистрации 1. Вероятность ошибки при действии КИ у метода стробирования меньше  [стробирование лучше].2. При дроблениях лучше интегральный метод  .1.3.1 Задача №1 Вычислить вероятность ошибки при регистрации методом стробирования, в соответствии с приложением 1.
Решение.     2. Синхронизация в системах ПДС Синхронизация – это процедура установления и поддержания определенных временных соотношений между двумя и более процессами. Различают поэлементную, групповую и цикловую синхронизацию. При поэлементной синхронизации устанавливаются и поддерживаются требуемые фазовые соотношения между значащими моментами переданных и принятых единичных элементов цифровых сигналов данных. Поэлементная синхронизация позволяет на приеме правильно отделить один единичный элемент от другого и обеспечить наилучшие условия для его регистрации. Групповая синхронизация – обеспечивает правильное разделение принятой последовательности на кодовые комбинации. Цикловая синхронизация – обеспечивает правильное разделение циклов временного объединения. 2.1 Устройства синхронизации с добавлением и вычитанием импульсов Устройство относится к классу без непосредственного воздействия на частоту генератора и является 3-х позиционным. При работающей системе синхронизации возможны три случая: Импульсы генератора без изменения проходят на вход делителя частоты. К последовательности импульсов добавляется 1 импульс. Из последовательности импульсов вычитается 1 импульс.  Задающий генератор вырабатывает относительно высокочастотную последовательность импульсов. Данная последовательность проходит через делитель с заданным коэффициентом деления. Тактовые импульсы с выхода делителя обеспечивают работу блоков системы передачи и также поступают в фазовый дискриминатор для ставнения. Фазовый дискриминатор определяет знак расхождения по фазе ЗМ и ТИ задающего генератора. Если частота ЗГ приема больше, то ФД формирует сигнал вычитания импульса для УДВИ, по которому запрещается прохождение одного импульса. Если частота ЗГ приема меньше, то импульс добавляется. В результате тактовая последовательность на выходе Dk сдвигается на  .Следующий рисунок иллюстрирует изменение положения тактового импульса в результате добавления и исключения импульсов. ТИ2 – в результате добавления, ТИ3 – в результате вычитания.  Роль реверсивного счетчика: В реальной ситуации принимаемые элементы имеют краевые искажения, которые изменяются случайным образом положение значащих моментов в разные стороны от идеального ЗМ. Это может вызвать ложную подстройку синхронизации. При действии КИ смещения ЗМ как в сторону опережения, так и в сторону отставания равновероятны. При смещении ЗМ по вине устройства синхронизации фаза стабильно смещается в одну сторону. Поэтому для уменьшения влияния КИ на погрешность синхронизации ставят реверсивный счетчик емкости S. Если подряд придет S сигналов на добавление импульса, говорящих об отставании генератора приема, то импульс добавится и следующий ТИ появится раньше на .Если сначала придет S-1 сигнал об опережении, потом S-1 об отставании, то добавления и вычитания не будет. 2.2 Параметры системы синхронизации с добавлением и вычитанием импульсов К основным параметрам системы синхронизации относятся: 1. Погрешность синхронизации  -- максимальное отклонение синхросигналов от их идеального положения, которое может произойти при работе устройства синхронизации с заданной вероятностью. (выражается в долях единичного интервала). Погрешность синхронизации – складывается из статической  , определяемой нестабильностью генераторов  и шагом коррекции  и динамической  , определенной краевыми искажениями. -коэффициент деления, где  - длительность единичного элемента, - шаг коррекцииВ силу конечности шага коррекции возникает погрешность:  Вследствие нестабильности генераторов, между двумя подстройками накапливается погрешность равная  где  – среднее число принимаемых подряд элементов одного знакаПериод корректирования – время между двумя подстройками, в общем случае определяется так:  ,однако нужно понимать, что – случайная величина и определяется структурой сообщения.Таким образом, общее выражение для статической погрешности:  .Динамическая погрешность синхронизации Динамическая погрешность вызывается краевыми искажениями единичных элементов. Краевые искажения имеют случайный характер со среднеквадратичным значением   . Следовательно, динамическая погрешность также случайная величина. Она подчиняется нормальному закону и имеет свое среднеквадратическое значение  . .Окончательно погрешность синхронизации определяется выражением:  .2. Время синхронизации (или вхождения в синхронизм)  -- время необходимое для корректирования первоначального отклонения синхроимпульсов относительно границ единичных принимаемых элементов. В момент включения расхождение по фазе между тактовыми импульсами передачи и приема – случайно и имеет в пределах от 0 до  . Выбирая наихудший случай, когда сдвиг фаз равен получим время синхронизации равное . Так как  ,  , то окончательно: .3. Время поддержания синхронизма  -- время, в течение которого отклонение синхроимпульсов от границ единичных элементов не превысит допустимый предел (  ) при прекращении работы устройства синхронизации по подстройке фазы.Эта задача аналогична задаче об автономных генераторах, рассмотренной нами выше, поэтому можно записать  .В качестве  - выбирают теоретическую исправляющую способность приемника  уменьшенную на погрешность синхронизации. Поэтому окончательно: .4. Вероятность срыва синхронизма  -- вероятность того, что под действием помех отклонение синхроимпульсов от границ единичных элементов превысит половину единичного интервала  . -можно уменьшить увеличив время усреднения сигналов коррекции фазы. Т.е. увеличив емкость реверсивного счетчика.Особенности синхронизации при старт-стопной передаче. Каждая кодовая комбинация начинается со ”старта” и оканчивается ”стопом”. Генератор приема (приемный распределитель) запускается при поступлении каждого сигнала ”старт” и останавливается по сигналу ”стоп” Накопившееся за время кодовой комбинации расхождения фазы каждый раз ликвидируется. + Высокая стабильность генераторов не требуется + Быстрое вхождение в синхронизм. 2.3 Расчет параметров системы синхронизации с добавлением и вычитанием импульсов 2.3.1 Задача № 2 Коэффициент нестабильности задающего генератора устройства синхронизации и передатчика К=10-6 . Исправляющая способность приемника m =40%. Краевые искажения отсутствуют. Постройте зависимость времени нормальной работы (без ошибок) приемника от скорости телеграфирования после выхода из строя фазового детектора устройства синхронизации. Будут ли возникать ошибки, спустя минуту после отказа фазового детектора, если скорость телеграфирования В = 9600 Бод? Решение. Время  , за которое расхождение по фазе достигнет e процентов от длительности единичного интервала, равно  Зависимость времени нормальной работы (без ошибок) приемника от скорости телеграфирования При скорости телеграфирования В = 9600 Бод время безошибочной работы равно  ,т.е. спустя минуту после отказа фазового детектора будут возникать ошибки. 2.3.2 Задача № 3 В системе передачи данных используется устройство синхронизации без непосредственного воздействия на частоту задающего генератора. Скорость модуляции равна В. Шаг коррекции должен быть не более D j к. Определите частоту задающего генератора и число ячеек делителя частоты, если коэффициент деления каждой ячейки равен двум. Значения В, D j к определите для своего варианта по формулам: B = 1000 + 10N=1070, D j к = 0,01 + 0,003N=0,031. Решение. Частота задающего генератора  Коэффициент деления делителя  Число ячеек делителя частоты  .2.3.3 Задача № 4 Рассчитать параметры устройства синхронизации без непосредственного воздействия на частоту задающего генератора со следующими характеристиками: время синхронизации не более 1 с, время поддержания синфазности не менее 10 с, погрешность синхронизации не более 10% единичного интервала t 0, среднеквадратическое значение краевых искажений равно 10%t 0 , исправляющая способность приемника 45%, коэффициент нестабильности генераторов k=10-6 . Определить реализуемо ли устройство синхронизации без непосредственного воздействия на частоту задающего генератора, обеспечивающее погрешность синхронизации e = 2,5% при данных условиях. Скорость модуляции для своего варианта рассчитайте по формуле: В=(600 + 10N)=670 Бод. Решение. Задано. - погрешность синхронизации  =0,1;- скорость телеграфирования  =670;- среднеквадратическое значение краевых искажений  =0,1;- исправляющая способность приемника  =0,45;- время синхронизации  =1с;- время поддержания синфазности  =10c.- коэффициент нестабильности генераторов k=10-6 Подлежат расчету: - частота задающего генератора  ;- коэффициент деления делителя m; - емкость реверсивного счетчика S. Расчет параметров сводится по существу к решению системы уравнений (7), (8), (9). Можно предложить следующий порядок расчета. 1. Допустимая величина коэффициента нестабильности задающего генератора.  , т.е. заданные генераторы удовлетворяют условию.2. Утроенное значение радикала  3. Емкость реверсивного счетчика  4. Коэффициент деления делителя  5. Частота задающего генератора  3. Корректирующее кодирование в системах ПДС От СПДС обычно требуется не только передавать сообщения с заданной скоростью передачи информации, но и обеспечивать при этом требуемую достоверность. Получив сообщение, пользователь должен быть с высокой степенью уверен, что отправлялось именно это сообщение. Помехи, действующие в канале, как известно, приводят к возникновению ошибок. Исходная вероятность ошибки в каналах связи обычно не позволяет достичь высокой степени достоверности без применения дополнительных мероприятий. К таким мероприятиям, обеспечивающим защиту от ошибок, относят применения корректирующих кодов. В общей структурной схеме СПДС задачу защиты от ошибок выполняет кодер и декодер канала, который иногда называют УЗО. Пусть имеется источник сообщений с объемом алфавита К. Поставим в соответствие каждому сообщению n - элементную двоичную последовательность. Всего последовательностей из n - элементов может быть  .Если  , то все последовательности (или кодовые комбинации) будут использоваться для кодирования сообщений, т.е. будут разрешенными.Полученный таким образом код называется простым, он не способен обнаруживать и исправлять ошибки. Для того, что бы код мог обнаруживать и исправлять ошибки необходимо выполнение условия  , при этом неиспользуемые для передачи комбинации (N0-K) называют запрещенными.Появление ошибки в кодовой комбинации будет обнаружено, если передаваемая разрешенная комбинация перейдет в одну из запрещенных. 3.1 Циклические коды Широкое распространение на практике получил класс линейных кодов, которые называются циклическими. Данное название происходит от основного свойства этих кодов: если некоторая кодовая комбинация принадлежит циклическому коду, то комбинация полученная циклической перестановкой исходной комбинации (циклическим сдвигом), также принадлежит данному коду.  .Вторым свойством всех разрешенных комбинаций циклических кодов является их делимость без остатка на некоторый выбранный полином, называемый производящим. Синдромом ошибки в этих кодах является наличие остатка от деления принятой кодовой комбинации на производящий полином. Эти свойства используются при построении кодов, кодирующих и декодирующих устройств, а также при обнаружении и исправлении ошибок. Описание циклических кодов и их построение удобно проводить с помощью многочленов (или полиномов). В теории циклических кодов кодовые комбинации обычно представляются в виде полинома. Так, n-элементную кодовую комбинацию можно описать полиномом (n-1) степени, в виде  .где  ={0,1}, причем  = 0 соответствуют нулевым элементам комбинации, а = 1 - ненулевым. При формировании комбинаций циклического кода часто используют операции сложения многочленов и деления одного многочлена на другой. Так,  ,поскольку  .Следует отметить, что действия над коэффициентами полинома (сложение и умножение) производятся по модулю 2. Для обнаружения ошибок в принятой кодовой комбинации достаточно поделить ее на производящий полином. Если принятая комбинация - разрешенная, то остаток от деления будет нулевым. Ненулевой остаток свидетельствует о том, что принятая комбинация содержит ошибки. По виду остатка (синдрома) можно в некоторых случаях также сделать вывод о характере ошибки, ее местоположении и исправить ошибку. Формирование базиса (производящей матрицы) циклического кода возможно как минимум двумя путями. Вариант первый. Составить единичную матрицу для простого исходного кода. Определить для каждой кодовой комбинации исходного кода группу проверочных элементов и дописать их в соответствующие строки матрицы. 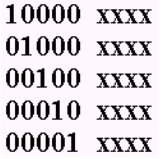 Полученная матрица и будет базисом циклического кода. Причем, в данном случае, разрешенные комбинации заведомо разделимы (т.е. информационные и проверочные элементы однозначно определены). Вариант второй. Дописать слева от КК, соответствующей образующему полиному циклического кода нули так, чтобы длина разрешенной кодовой комбинации равнялась n. Получить остальные разрешенные кодовые КК базиса, используя циклический сдвиг исходной. (В базисе должно быть k – строк) В данном случае код будет неразделимым. Получив базис ЦК, можно получить все разрешенные комбинации, проводя сложение по модулю 2 кодовых комбинаций базиса в различных сочетаниях и плюс НУЛЕВАЯ. Циклические коды достаточно просты в реализации, обладают высокой корректирующей способностью (способностью исправлять и обнаруживать ошибки) и поэтому рекомендованы МСЭ-Т для применения в аппаратуре ПД. Согласно рекомендации V.41 в системах ПД с ОС рекомендуется применять код с производящим полиномом  3.2 Построение кодера и декодера Рассмотрим код (9,5) образованный полиномом  .Разрешенная комбинация циклического кода  образуется из комбинации простого (исходного) кода путем умножения ее на  и прибавления остатка R(x) от деления  на образующий полином .Умножение полинома на одночлен  эквивалентно добавлению к двоичной последовательности соответствующей G(x) , r - нулей справа. Пусть  тогда  Для реализации операции добавления нулей используется r-разрядный регистр задержки. Рассмотрим более подробно операцию деления:  Как видим из примера, процедура деления одного двоичного числа на другое сводится к последовательному сложению по mod2 делителя [10011] с соответствующими членами делимого [10101], затем с двоичным числом, полученным в результате первого сложения, далее с результатом второго сложения и т.д., пока число членов результирующего двоичного числа не станет меньше числа членов делителя. Это двоичное число и будет остатком  . Построение формирователя остатка циклического кода. Структура устройства осуществляющего деление на полином полностью определяется видом этого полинома. Существуют правила позволяющие провести построение однозначно. Сформулируем правила построения ФПГ. Число ячеек памяти равно степени образующего полинома r. Число сумматоров на единицу меньше веса кодирующей комбинации образующего полинома. Место установки сумматоров определяется видом образующего полинома.  Сумматоры ставят после каждой ячейки памяти, (начиная с нулевой) для которой существует НЕнулевой член полинома. Не ставят после ячейки для которой в полиноме нет соответствующего члена и после ячейки старшего разряда. 4. В цепь обратной связи необходимо поставить ключ, обеспечивающий правильный ввод исходных элементов и вывод результатов деления. Структурная схема кодера циклического кода (9,5). Полная структурная схема кодера приведена на следующем рисунке. Она содержит регистр задержки и рассмотренный выше формирователь проверочной группы.  Рассмотрим работу этой схемы 1. На первом этапе К1– замкнут К2 – разомкнут. Идет одновременное заполнение регистров задержки и сдвига информ. элементами (старший вперед!) и через 4 такта старший разряд в ячейке №4 2. Во время пятого такта К2 – замыкается а К1 – размыкается с этого момента в ФПГ формируется остаток. Одновременно из РЗ на выход выталкивается задержание информационные разряды. За 5 тактов (с 5 по 9 включительно) в линию уйдут все 5-информационных элемента. К этому времени в ФПГ сформируется остаток 3. К2 – размыкается, К1 – замыкается и в след за информационными в линию уйдут элементы проверочной группы. 4. Одновременно идет заполнение регистров новой комбинацией. Второй вариант построения кодера ЦК. Рассмотренный выше кодер очень наглядно отражает процесс деления двоичных чисел. Однако можно построить кодер содержащий меньшее число элементов т.е. более экономичный. Устройство деления на производящий полином 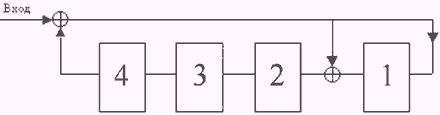 можно реализовать в следующем виде: За пять тактов в ячейках будет сформирован такой же остаток от деления, что и в рассмотренном выше Формирователе проверочной группы. (ФПГ). За эти же 5 тактов информационные разряды, выданные сразу на модулятор. Далее в след за информационными уходят проверочные из ячеек устройств деления. Но важно отключить обратную связь на момент вывода проверенных элементов, иначе они исказятся. Окончательно структурная схема экономичного кодера выглядит так.  - На первом такте Кл.1 и Кл.3 замкнуты, информационные элементы проходят на выход кодера и одновременно формируются проверочные элементы. - После того, как в линию уйдет пятый информационный элемент, в устройстве деления сформируются проверочные; - на шестом такте ключи 1 и 3 размыкаются (разрываются обратная связь), а ключ 2 замыкается и в линию уходят проверочные разряды. Ячейки при этом заполняются нулями и схема возвращается в исходное состояние. Пример декодирования комбинации ЦК. Положим, получена комбинация H(х)=111011010 Реализуя алгоритм определения ошибок, определим остаток от деления вектора соответствующего ошибке в старшем разряде Х8 на производяший полином P(x)=X4+X+1 X8 X2+X+1 X8+X5+X4 x4+x+1 X5+X4 X5+X2+X X4+X2+X X4+X+1 X2+1=R0(X)=0101 Разделим принятую комбинацию на образующий полином H(x) · x 1110110100 10011 10011 111111 5-т 11101 10011 6-т 11100 10011 7-т 11111 10011 8-т 11000 10011 9-т 10110 = R(X)  R0(X)10011 10-т 0101=R0(x) Полученный на 9-м такте остаток, как видим, не равен R0(X). Значит необходимо умножить принятую комбинацию на Х и повторить деление. Однако результаты деления с 5 по 9 такты включительно будут такими же, значит необходимо продолжить деление после девятого такта до тех пор, пока в остатке не будет R0(Х). В нашем случае это произойдет на 10 такте, при повышении степени на 1. Значит ошибки во втором разряде. Декодер циклического кода с исправлением ошибки Если ошибка в первом разряде, то остаток R0(X)=10101 появления после девятого такта в ячейках ФПГ. Если во втором по старшинству то после 10го; в третьем по старшинству то после 11го; в четвертом по старшинству то после 12го в пятом по старшинству то после 13го в шестом по старшинству то после 14го в седьмом по старшинству то после 15го в восьмом по старшинству то после 16го в девятом по старшинству то после 17го. На 10 такте старший разряд покидает регистр задержки и проходит через сумматор по модулю 2. Если и этому моменту остаток в ФПГ=R0(X), то логическая 1 с выхода дешифратора поступит на второй вход сумматора и старший разряд инвертируется. В нашем случае инвертируется второй разряд на 11 такте. 3.2.1 Задача № 5 Записать кодовую комбинацию циклического кода для случая, когда производящий полином имеет вид Р(х)=х3+х2+1 (для N= 0,1,2,3,4) и Р(х)=х3+х+1 (для N=5,6,7,8,9). Кодовая комбинация, поступающая от источника сообщений имеет К=4 элементов и записывается в двоичном виде как число, соответствующее (N+3=10) для N=6¸ 9. Нарисовать кодирующее и декодирующее устройство с обнаружением ошибок и "прогнать" через кодирующее устройство исходную кодовую комбинацию с целью формирования проверочных элементов. Решение.  Определение остатка от деления  Кодовая комбинация G(x)=1010011  Кодирующее устройство.
Результат "прогона" через кодирующее устройство исходной кодовой комбинации  Декодер с обнаружением ошибок 4. Системы ПДС с обратной связью В зависимости от назначения ОС различают системы: с решающей ОС (РОС) с информационной (ИОС) Общее в алгоритме работы систем с ОС в простейшем случае, то что после передачи некоторой порции информации передатчик прямого канала ожидает сигнала, либо на выдачу следующей порции, либо на повторную передачу предыдущей. Принципиальное отличие систем РОС и ИОС состоит в том, где принимается решение о дальнейшем поведении системы. В системах с РОС решение принимается на приёме, а в системах с ИОС – на передаче. Для организации обратной связи и в тех и в других системах используется обратный канал. 4.1 Системы с информационной обратной связью Рассмотрим структуру системы ПДС с ИОС  Алгоритм. Кодовые комбинации, поступающие в приёмник передаются по обратному каналу в передатчик. На передающей стороне сравниваются комбинации, которые передавались – с возвращёнными. Если они совпадают, то решающее устройство формирует сигнал на продолжение передачи и в прямой канал выдаются новые данные, а приёмник выдаёт принятые кодовые комбинации получателю. Если при сравнении обнаруживаются отличия, то передатчик вновь повторяет переданные ранее КК. Информация передаваемая по каналу с ОС – называется квитанцией. Системы с ИОС в которых осуществляется полная передача принятых кодовых комбинаций по обратному каналу называются ретрансляционные. Чаще приёмник формирует специальные сигналы, имеющие меньший объём, чем полезная информация переданная по прямому каналу т. е. квитанция меньше – укороченная ИОС. 4.2 Системы с решающей обратной связью Наиболее распространёнными среди систем с РОС являются : системы с ожиданием (РОС - ОЖ); с непрерывной передачей информации и блокировкой с адресным переспросом Рассмотрим более подробно систему (РОС - ОЖ) В данной системе после передачи кодовой комбинации система ожидает сигнала подтверждения, и только после этого происходит передача следующей КК.  Структурная схема СПД с РОС – ОЖ Алгоритм работы: КК выдаваемая ИС поступает в кодер, и одновременно в накопитель передачи Н пер. Кодер добавляет проверочные разряды в соответствии с алгоритмом ПУ кодирования. Далее КК модулируется (УПС) и выдаётся в прямой канал связи. Спустя некоторое время, необходимое для передачи по каналу tp , КК поступает в приёмник. После УПС приёма информационная часть КК записываются в накопитель приёма, и одновременно с этим вся КК поступает в ПУ декодер. Если декодер не обнаружил ошибку, то РУ принимает решение о качестве приёма и выдаёт соответствующий сигнал на УУ. УУ – формирует сигнал для выдачи принятой порции информации получателю и команду для формирования сигнала ''подтверждения''. Данный сигнал пройдя через ОК дешифруется ДСОС и поступает в УУ пер. По его приходу УУ передачи стирает старую комбинацию из Н пер и сигнализирует ИС о выдачи следующей порции информации (КК). Если в результате декодирования обнаружена ошибка, то решающее устройство выдаёт соответствующий сигнал в УУ приёма. УУ стирает принятую КК из Н пр и даёт команду на формирование сигнала ''переспрос''. После получения сигнала ''переспрос'' УУ пер запрещает ИС выдавать следующую КК, и подаёт сигнал накопителю, который посылает записанную в нём КК в декодер – повторно. 4.2.1 Задача № 6 Рассчитать скорость передачи информации для системы РОС с ОЖ. Ошибки в канале не зависимы Pош=(N/2)-10-3. Построить графики зависимости R(g 1,g 2,g 3) от длины блока. Найти оптимальную длину блока. Если время ожидания tош=0,6× tбл (при к=8). Блок передаваемый в канал имеет значения: к=8,16,24,32,40,48,56. Число проверочных элементов: r=6. Длина блока в канале определяется по формуле n=ki+r. Решение. Коэффициенты уменьшения скорости.   , т.к.  , а tбл=nτ0 , то  Скорость передачи информации   Зависимость скорости передачи информации от длины блока Оптимальная длина блока – 8 элементов. 4.2.2 Задача №7 Определить вероятность неправильного приема в системе с РОС-ОЖ в зависимости от длины блока и построить график. Блок передаваемый в канал имеет значения: к=8,16,24,32,40,48,56. Число проверочных элементов: r=6. Длина блока в канале определяется по формуле n=ki+r. Ошибки в канале считать независимыми. Вероятность ошибки на элемент Pош=(N/2)-10-3. Решение. Вероятность неправильного приема   Список литературы 1. Передача дискретных сообщений: Учебник для вузов / В. П. Шувалов, Н. В. Захарченко, В. О. Шварцман и др.; Под ред. В. П. Шувалова. – М.: Радио и связь, 1990-464с. 2. Конспект лекций по курсу “Основы построения телекоммуникационных систем и сетей” СибГУТИ. Размещено на Studwood.ru | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||