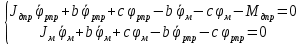Курсовая работа, Тау. КурПР.Таурило 3331504.90301. Курсовая работа по дисциплине "Теория автоматического управления" "Система управления модуля поворота промышленного робота" Выполнил студент Таурило В. В. гр. 333150490301
 Скачать 1.15 Mb. Скачать 1.15 Mb.
|
|
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ “САНКТ-ПЕТЕРБУРГСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ПЕТРА ВЕЛИКОГО” Институт машиностроения, материалов и транспорта Кафедра теории механизмов и машин Курсовая работа по дисциплине “Теория автоматического управления” “Система управления модуля поворота промышленного робота” Выполнил студент _____________________ Таурило В.В. гр. 3331504/90301 Работу принял _____________________ Терёшин В.А. Санкт-Петербург 2021 г. СОДЕРЖАНИЕТехническое задание 3 Техническое задание на выполнение курсовой работы по теории автоматического управления Вариант №104
Выбрать параметры аналогового регулятора модуля поворота промышленного робота. Углы поворота ротора двигателя φр и выходного вала редуктора φм измеряются и пропорциональные им сигналы qp = kφр/iи qм = kφм подаются на блок сравнения с задающим напряжением q* = kφ*. k =100В/рад –коэффициент преобразования измерителя угла поворота; i =50–передаточное отношение редуктора; φ* – требуемый закон перемещения модуля поворота. Сигналы рассогласования kψр = qр - q* и kψм = qм - q* поступает на ПИ-регулятор. Сформированный отрицательной обратной связью сигнал управления поступает на вход двигателя. 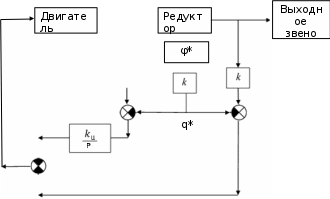     φр φм φм u   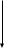   k/i   qм qр   kψр     kψм 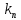 Момент инерции приводимого в движение выходного звена JM = 1 кгм2. Жесткость и коэффициент демпфирования редуктора, приведенные к выходному валу с = 104 Нм, b = 100 Нмс. Момент инерции ротора двигателя Jд=2  10-4кгм2. При расчетах необходимо использовать линейную динамическую характеристику двигателя 10-4кгм2. При расчетах необходимо использовать линейную динамическую характеристику двигателя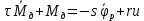 Крутизна механической характеристики и собственная постоянная времени двигателя s= 0,05 Нмс, τ = 0,003 с. Коэффициент r= 0,7 Нм/В. Мд – движущий момент. Записать уравнения движения механической части, как системы с двумя степенями свободы, приведенную динамическую характеристику двигателя и уравнение системы управления. Разрешить полученную систему четырех уравнений в переменных Лапласа относительно четырех неизвестных. Сформировать знаменатель передаточных функций. Определить область устойчивости замкнутой системы управления с помощью критерия Стодолы и Рауса-Гурвица. На диаграмме с D-разбиением при φ* ≡  построить области крутящего момента {М}, в которой │Мм│max< 150 Нм, и управляющего сигнала {u}, в которой │u│max< 220В. В области одновременного выполнения этих двух условий построить линии равных длительностей tп= tп(kп; kд) переходных процессов при нулевых начальных условиях. Под длительностью переходного процесса будем понимать время, после которого угловая ошибка | ψм | не превосходит 10% от φ*. Построить оптимальную кривую построить области крутящего момента {М}, в которой │Мм│max< 150 Нм, и управляющего сигнала {u}, в которой │u│max< 220В. В области одновременного выполнения этих двух условий построить линии равных длительностей tп= tп(kп; kд) переходных процессов при нулевых начальных условиях. Под длительностью переходного процесса будем понимать время, после которого угловая ошибка | ψм | не превосходит 10% от φ*. Построить оптимальную кривую Найти значения параметров kд и kп из области {L}, соответствующие наименьшей длительности переходных процессов. Проиллюстрировать результаты расчетов при трех различных значениях (kд;kп), построив графики действительного перемещения φм, сигнала рассогласования 𝜓p,упругой деформации редуктора φр/i– φм, крутящего момента на выходе редуктора Мм, движущего момента, приведенного к выходу редуктора Мдпр=Мдiи сигнала управления uкак функций времени. Введение В данной курсовой работе стоит задача выбрать параметры аналогового регулятора модуля поворота промышленного робота. Основные цели: составление уравнений движения, проверка устойчивости, построение области устойчивости, исследование переходных процессов, построение линий равной длительности и линий уровня, подбор оптимальных коэффициентов. В работе использовалась программа MathCad, с помощью нее производилось решение матричных уравнений, дифференциальных уравнений, проводилось преобразование Лапласа и обратное преобразование Лапласа. Данная работа была осуществлена, для того, чтобы рассчитать оптимальное управление для стабильной плавной работы модуля поворота промышленного робота. Математическая модель системы управления 1.1. Уравнения движения механической части М  еханическая часть модуля поворота состоит из ротора электродвигателя, редуктора и выходного звена. На рис. 1 показана кинематическая схема механизма. Рис. 1. Кинематическая схема механизма Для формирования динамической модели и получения уравнений движения механической части запишем её кинетическую энергию.
Индекс «ж» соответствует абсолютно жесткому редуктору.
Следовательно
где 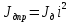 – момент инерции ротора двигателя, приведенный к координате φм. Заметим, что – момент инерции ротора двигателя, приведенный к координате φм. Заметим, что 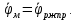 Запишем элементарную работу внешних сил на возможном перемещении. Внешней силой является только движущий момент электромагнитных сил, приложенный к ротору двигателя Мд. Тогда Запишем элементарную работу внешних сил на возможном перемещении. Внешней силой является только движущий момент электромагнитных сил, приложенный к ротору двигателя Мд. Тогда
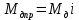 – движущий момент, приведенный к координате φм . – движущий момент, приведенный к координате φм .Сформируем динамическую модель механической части в виде цепной системы, учитывающей упругие свойства передаточного механизма. 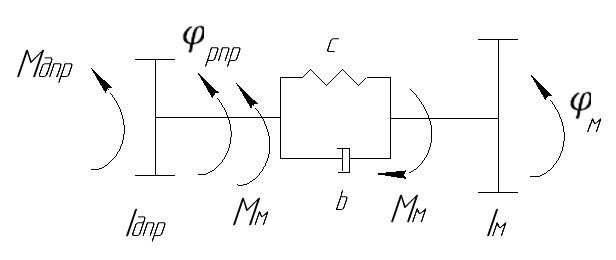 Рис. 2. Динамическая модель механической части модуля поворота Момент на выходном валу Мм связан с деформацией 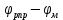 линейным упруго-диссипативным соотношением линейным упруго-диссипативным соотношением
где с – коэффициент жесткости редуктора, приведенный к координате 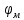 ; b – коэффициент диссипации (демпфирования, вязкого трения и т.п.). ; b – коэффициент диссипации (демпфирования, вязкого трения и т.п.).Запишем уравнения движения механической части как двухмассовой системы с двумя степенями свободы в соответствии с рис. 2.
или
Эти уравнения позволяют определить 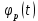 и и 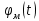 при заданном Мд(t). при заданном Мд(t).1.2 Характеристики двигателя Электродвигатель постоянного тока при постоянном управляющем сигнале имеет следующую зависимость момента сопротивления (движущий момент) от угловой скорости ротора двигателя 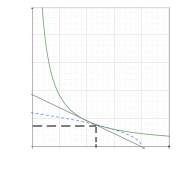 Рис. 3. Статическая характеристика двигателя  Индекс «н» - номинальная величина; «хх» - холостой ход.  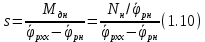 S – крутизна статической характеристики двигателя (не зависит от величины управления). 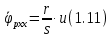 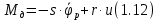 В силу переходности процессов необходимо учитывать время запаздывания движущего момента относительно управляющего сигнала: 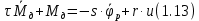 Это динамическая характеристика двигателя.  – собственная постоянная времени двигателя. Приведем характеристику к координате – собственная постоянная времени двигателя. Приведем характеристику к координате 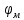  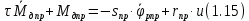 где 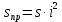 , ,  – крутизна и коэффициент пропорциональности, приведенные к выходному звену. – крутизна и коэффициент пропорциональности, приведенные к выходному звену.1 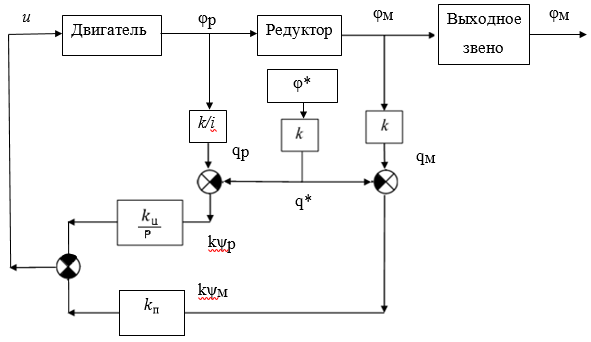 .3 Передаточная функция цепи обратной связи  Посчитаем передаточную функцию цепи обратной связи. Посчитаем передаточную функцию цепи обратной связи. Уравнение сигнала управления:  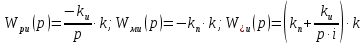 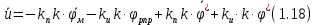 1.4 Операторная форма системы уравнений движения Дополним систему уравнений механической части динамической характеристикой двигателя и уравнением сигнала управления: 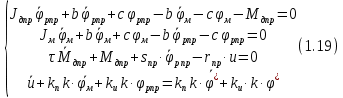 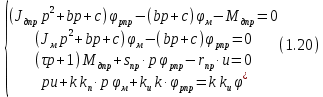 1.5 Структурная схема системы уравнения   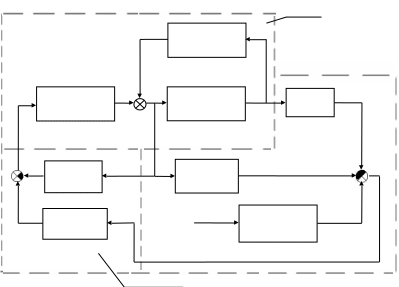 1.6 Матричная форма системы уравнений движения в изображениях по Лапласу Подействуем оператором Лапласа на систему уравнений при нулевых начальных условиях 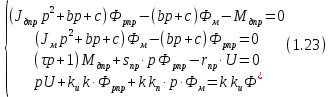  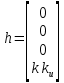  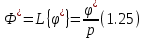 2. Область устойчивости системы управления в пространстве (kп; kи) 2.1 Характеристическое уравнение. Характеристическим уравнением называется равенство нулю определителя матрицы А. 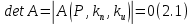   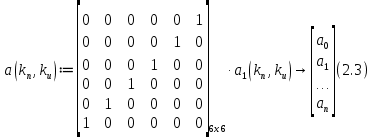 Сформируем характеристический полином, подставив в него все заданные числовые значения параметров.  Выпишем аналитические зависимости коэффициентов полинома от 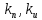 . .2.2 Критерии устойчивости Стодолы и Раусса-Гурвица.  Для определения устойчивости характеристического полинома и построения области устойчивости в пространстве 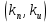 сформируем матрицу Гурвица. сформируем матрицу Гурвица.Выпишем угловые миноры: В соответствии с критериями Стодолы и Раусса-Гурвица все коэффициенты полинома и угловые миноры должны быть больше нуля. 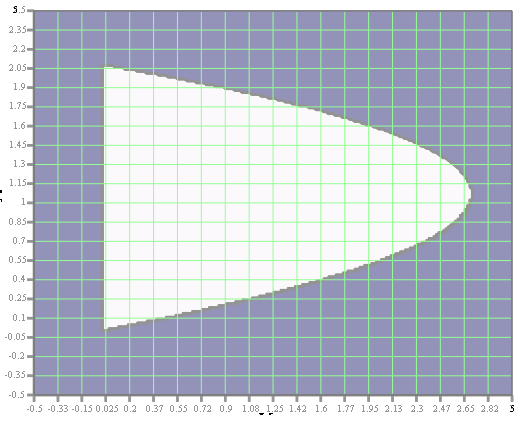 В среде MathCad это условие записывается функцией Хевисайда. Рисунок 4 – область устойчивости 2.3 Проверка устойчивости с помощью годографа Михайлова Сгруппируем полином по четным и нечетным степеням р и запишем полином Михайлова.  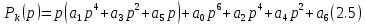  Построим его годограф для выбранной точки ( 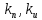 ) ) 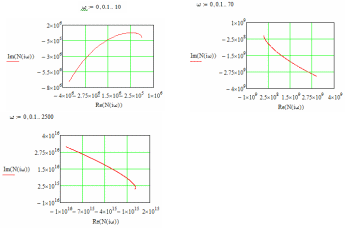 В случае обхода годографа Михайлова точки начала координат (0;0) на угол равный 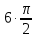 полином полином 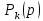 является устойчивым. Для наглядности далее приведено 4 графика годографа Михайлова при разных значениях частот. является устойчивым. Для наглядности далее приведено 4 графика годографа Михайлова при разных значениях частот.Рисунок 5 – Годограф Михайлова 3 Исследование переходных процессов. 3.1 Обратное преобразование Лапласа. Система уравнений (1.19) была приведена к виду (1.21). Для её решения найдём столбец неизвестных изображений по Лапласу. Задаём 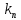 и и  . .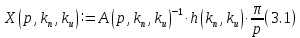  Для упрощения работы MathCad до команды invlaplace следует применить разложение на простейшие дроби. 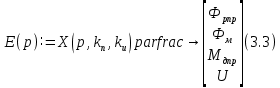 и далее 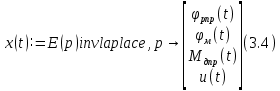 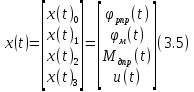 Р 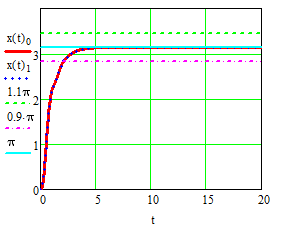 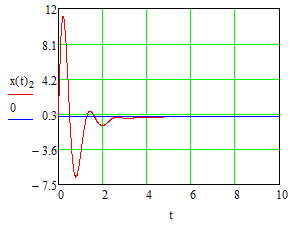 исунок 6- График угла поворота ротора двигателя и выходного вала редуктора. Р  исунок 7- График движущего момента. Рисунок 8- График сигнала управления. 3.2. Особенности переходных процессов в области устойчивости и на ее границе. Посмотрим зависимость системы при трех различных значениях пары коэффициентов. 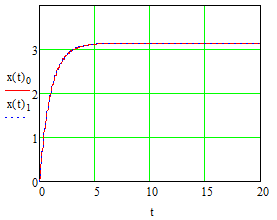 На рисунках 9,10,11 изображены графики при  и и  середина области. середина области.Р  исунок 9- График угла поворота ротора двигателя и выходного вала редуктора. Р 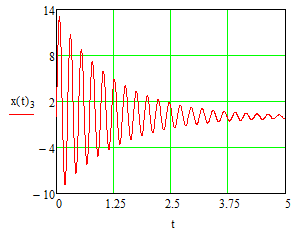 исунок 10- График движущего момента. Рисунок 11- График сигнала управления. 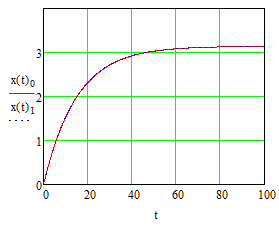 На рисунках 12,13,14 изображены графики при 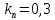 и и  граница области. граница области.Р 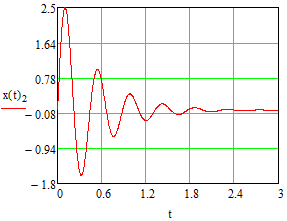 исунок 12- График угла поворота ротора двигателя и выходного вала редуктора. Р 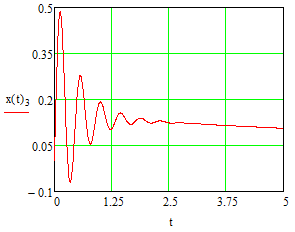 исунок 13- График движущего момента. Рисунок 14- График сигнала управления. 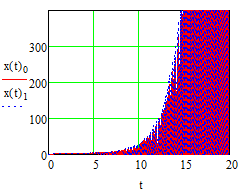 На рисунках 15,16,17 изображены графики при 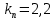 и и 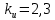 вне границы области. вне границы области.Р 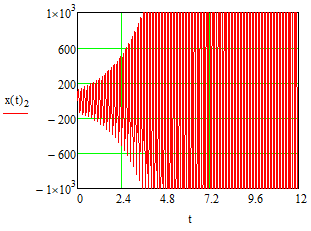 исунок 15- График угла поворота ротора двигателя и выходного вала редуктора. Рисунок 16- График движущего момента. 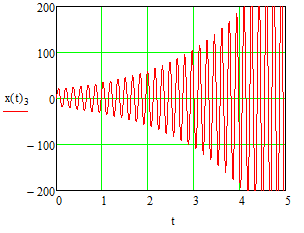 Рисунок 17- График сигнала управления. Данная пара коэффициентов лежит вне области устойчивости т.к. функция расходится с течением времени, это видно по графикам.   На рисунке 18 проиллюстрировано распределение корней характеристического полинома при коэффициентах 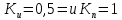 , найденных с помощью команды (solve ) , найденных с помощью команды (solve ) Для того, чтобы полином был устойчивым, его корни должны находиться в левой полуплоскости. На рисунке 18 представлены корни характеристического полинома на комплексной плоскости: Рисунок 18 - корни характеристического полинома на комплексной плоскости. 3.3. Область допустимых значений крутящего момента на выходном валу передаточного механизма. 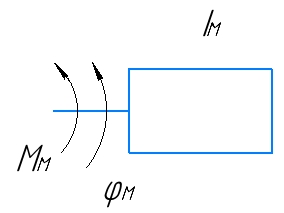 По техническому заданию крутящий момент 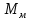 на выходном валу редуктора не должен превышать 150 Нм. Для его определения применим принцип освобождения от связей и заменим выходной вал редуктора крутящим моментом на выходном валу редуктора не должен превышать 150 Нм. Для его определения применим принцип освобождения от связей и заменим выходной вал редуктора крутящим моментом 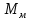 . .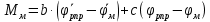 Из рисунка видно, что уравнение движения механизма модуля поворота совпадает со вторым уравнение (1.6). 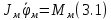  Закон движения Закон движения 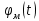 был получен ранее, поэтому был получен ранее, поэтому (3.2) На области устойчивости с помощью перебора точек построить линию на которой  Определить область, где 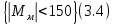 Р 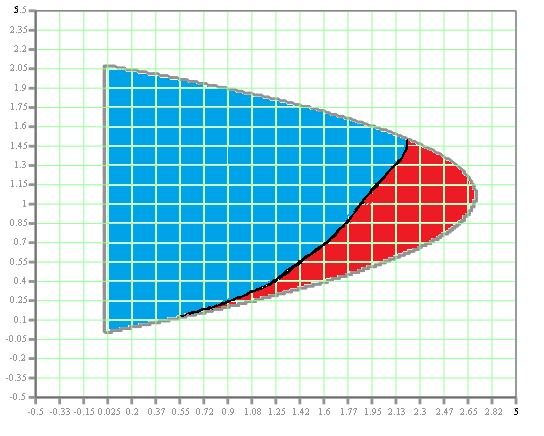 исунок 19 - Область допустимых значений крутящего момента (голубой цвет - момент <150, красный – момент > 150) 3.4. Область допустимых значений управляющего сигнала. По техническому заданию управляющий сигнал U не должен превышать 220 В. Функция 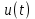 была получена ранее, поэтому была получена ранее, поэтому 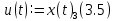 На области устойчивости с помощью перебора точек надо построить линию на которой: 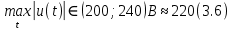 и  определим область: 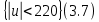 Рисунок 20 - Область допустимых управляющего сигнала (голубой цвет – вся область подходит под условие) В заключении требуется определить область, в которой выполняются все три условия одновременно: устойчивость, допустимое значение крутящего момента и допустимое значение управляющего сигнала. 3.5. Линии равных длительностей переходных процессов. Минимальная и максимальная длительности. 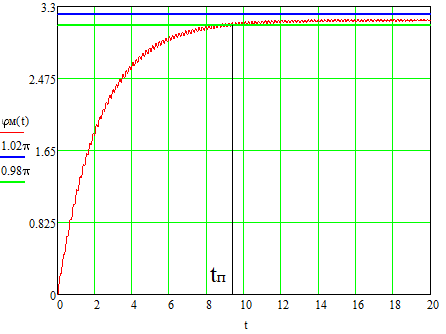 Длительностью переходного процесса называется время 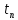 , после которого угол , после которого угол 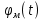 не выходит из 2% - отклонение от не выходит из 2% - отклонение от 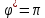 . . Рисунок 21 - Длительность переходного процесса. 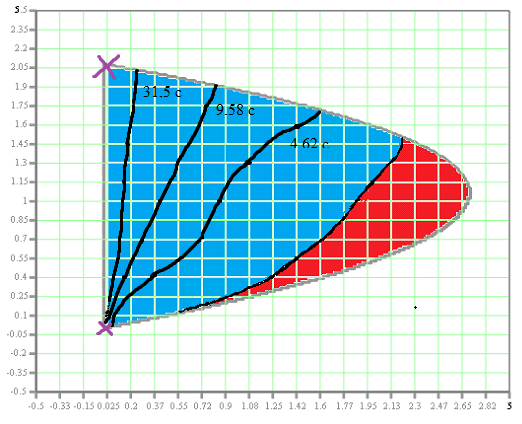 С помощью перебора точек на области выполнения трёх условий построить несколько линий равных длительностей с погрешностью 20% и указать точки с минимальной и максимальной длительностями. С помощью перебора точек на области выполнения трёх условий построить несколько линий равных длительностей с погрешностью 20% и указать точки с минимальной и максимальной длительностями.Рис 22 - Линии равных длительностей, верхняя точка -  , нижняя точка - , нижняя точка - 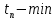 . .По итогу было найдено 3 линии равных длительностей со временем длительности 31,5с ; 9,58с и 4,62с. Также были отмечены точки с максимальной и минимальной длительностью переходного процесса:  На графиках показаны только части линий, остальная их часть находится вне области устойчивости. Предполагается, что линии должны замыкаться, но мы не можем этого наблюдать. По графикам видно, что наибольшая длительность наблюдается на левой границе области устойчивости, с смещением направо, длительность постепенно уменьшается, причем, вблизи к верхней границе наблюдается сильная волатильность графика На графиках показаны только части линий, остальная их часть находится вне области устойчивости. Предполагается, что линии должны замыкаться, но мы не можем этого наблюдать. По графикам видно, что наибольшая длительность наблюдается на левой границе области устойчивости, с смещением направо, длительность постепенно уменьшается, причем, вблизи к верхней границе наблюдается сильная волатильность графика 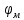 , ближе к нижней границе наоборот, функция ведет себя спокойнее. , ближе к нижней границе наоборот, функция ведет себя спокойнее.4. Оптимальное управление. При проектировании системы управления необходимо уменьшать управляющие сигналы и динамические ошибки  Эти взаимоисключающие требования можно свести к единому функционалу качества. Эти взаимоисключающие требования можно свести к единому функционалу качества.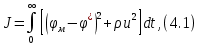 где 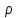 – весовой множитель. В пространстве ( – весовой множитель. В пространстве ( надо найти надо найти  , который определит ( , который определит (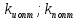 ). В курсовом проекте необходимо найти оптимальную точку в области выполнения трёх условий. Так как оптимальная точка ( ). В курсовом проекте необходимо найти оптимальную точку в области выполнения трёх условий. Так как оптимальная точка (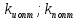 ) зависит от ) зависит от 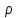 , то надо построить оптимальную кривую при , то надо построить оптимальную кривую при 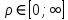 по нескольким значениям по нескольким значениям 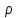 . Эта задача оптимального управления может быть решена с помощью Уравнения Лурье. Однако из-за её громоздкости воспользуемся перебором точек. . Эта задача оптимального управления может быть решена с помощью Уравнения Лурье. Однако из-за её громоздкости воспользуемся перебором точек.4.1. Линии равных уровней интегрального показателя качества при нулевом весовом множителе. При  для расчёта интеграла (4.1) можно ограничиться временем для расчёта интеграла (4.1) можно ограничиться временем 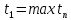 : : 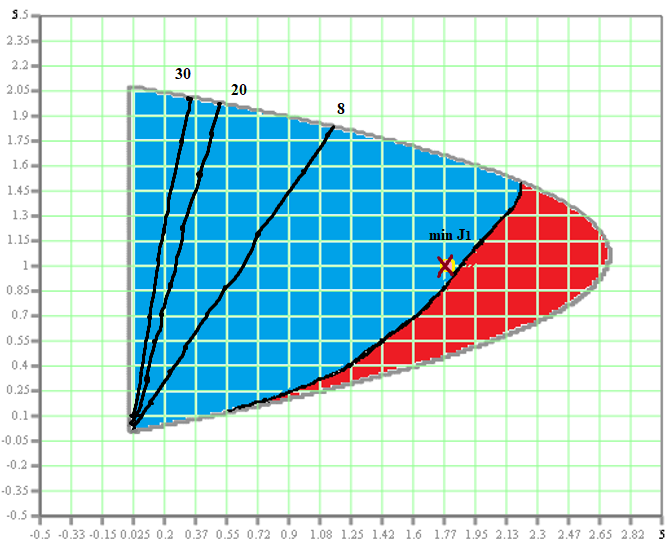 С помощью перебора точек построить несколько (3…4) линий уровня, указав С помощью перебора точек построить несколько (3…4) линий уровня, указав 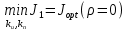 . . Рис 23 - Линии равных уровней показателя качества при нулевом весовом множителе. Судя по графикам, максимальные значения 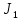 лежат ближе к левой границе области устойчивости верхний угол. С увеличением коэффициента лежат ближе к левой границе области устойчивости верхний угол. С увеличением коэффициента  , то есть при сдвиге в правую часть, значения интегрального показателя качества уменьшаются. Минимум наблюдается в точке , то есть при сдвиге в правую часть, значения интегрального показателя качества уменьшаются. Минимум наблюдается в точке 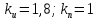 и его значение и его значение 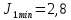 . Соответственно, линиями уровня разделены значения интеграла, интеграл от всех точек, которые к примеру лежат левее линии 30, будет больше 30, также как и интеграл от всех точек лежащих левее линии 8, будет меньше 8. . Соответственно, линиями уровня разделены значения интеграла, интеграл от всех точек, которые к примеру лежат левее линии 30, будет больше 30, также как и интеграл от всех точек лежащих левее линии 8, будет меньше 8.4.2. Линии равных уровней интегрального показателя качества при бесконечно большом весовом множителе. При больших 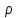 в (4.1) можно пренебречь первым слагаемым, сохранив вид (4.2). Общий вид зависимости не зависит от множителя в (4.1) можно пренебречь первым слагаемым, сохранив вид (4.2). Общий вид зависимости не зависит от множителя 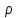 : :  Необходимо аналогично (4.2) построить для (4.3) несколько линий уровня, указав точку 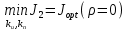 , и описать её, сравнив графики , и описать её, сравнив графики 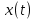 с другими точками. с другими точками.Рис 24 - Линии равных уровней показателя качества при бесконечно большом весовом множителе. Из графика видно, что меньшие значения интегрального показателя качества лежат на левой границе, при этом, минимальная точка 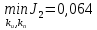 и имеет координаты и имеет координаты  . Удаляясь от левой границы, в нижней половине области устойчивости значения интеграла меньше, чем в верхней половине. Линии уровня лежат в области устойчивости не полностью и замыкаются где-то за областью. . Удаляясь от левой границы, в нижней половине области устойчивости значения интеграла меньше, чем в верхней половине. Линии уровня лежат в области устойчивости не полностью и замыкаются где-то за областью. 4.3. Линии равных уровней интегрального показателя качества при весовом множителе, определенном на основе ограничений. Основным методом определения весовых множителей является их задание как (4.4) для 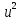 и (4.5) для ошибки: и (4.5) для ошибки: 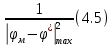 Примем  а а 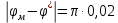  Так как характер поверхности 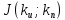 не зависит от множителя, то её минимум определяется как: не зависит от множителя, то её минимум определяется как: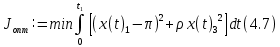 С помощью перебора точек надо построить несколько линий уровней для: 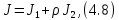 у  казав точку 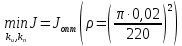 и описать её, сравнив графики и описать её, сравнив графики 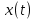 с другими точками. с другими точками.Рис 25 - Линии равных уровней показателя качества при определенном на основе ограничений весовом множителе. На графике были построены линии уровня, область ограниченная линией со значением 50 имеет внутри все точки меньше 50, по удалению от этой области значения интеграла быстро увеличиваются, а минимум  наблюдается в точке с координатами наблюдается в точке с координатами 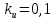 ; ; 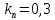 и равен и равен 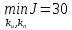 . .4.4. Анализ переходных процессов на оптимальной кривой. Для построения кривой (4.9) 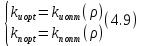 может потребоваться поиск (4.10) для других 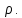 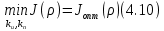 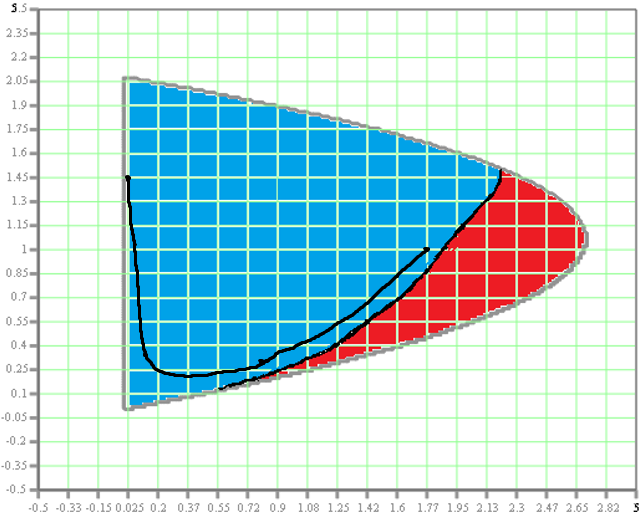 Необходимо сравнить переходные процессы на оптимальной кривой между собой и с другими точками области выполнения трёх условий. Найти качественные отличия. Рис 26 – Оптимальная кривая. 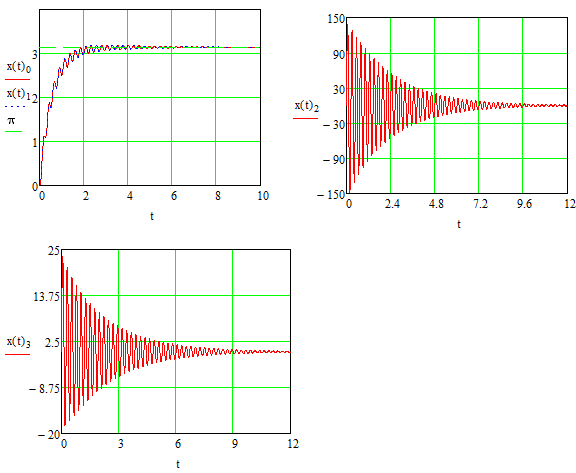 На рисунке 27 представлены графики угла поворота ротора двигателя и выходного вала редуктора, график движущего момента и график управляющего сигнала для  и коэффициентов и коэффициентов  ; ;  Рис 27 – Графики 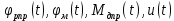 для для  . .Исходя из анализа графиков можно прийти к следующему: В данной точке быстрее всего ошибка по углу стремится к нулю При этом высокое значение движущего момента с медленным затуханием. Медленное затухание управляющего сигнала 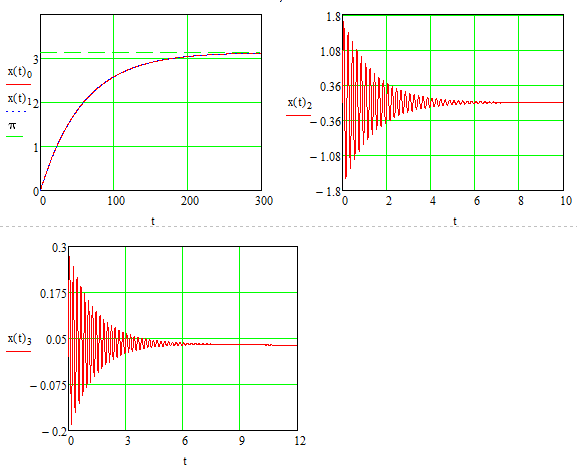 На рисунке 28 представлены графики угла поворота ротора двигателя и выходного вала редуктора, график движущего момента и график управляющего сигнала для 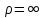 и коэффициентов и коэффициентов  ; ; 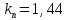 Рис 28 – Графики 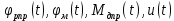 для для 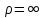 Исходя из анализа данных графиков можно сделать вывод, что несмотря на то, что движущий момент и управляющий сигнал не велики и достаточно быстро затухают, есть еще графики углов поворота, ошибки которых очень долго обнуляются. 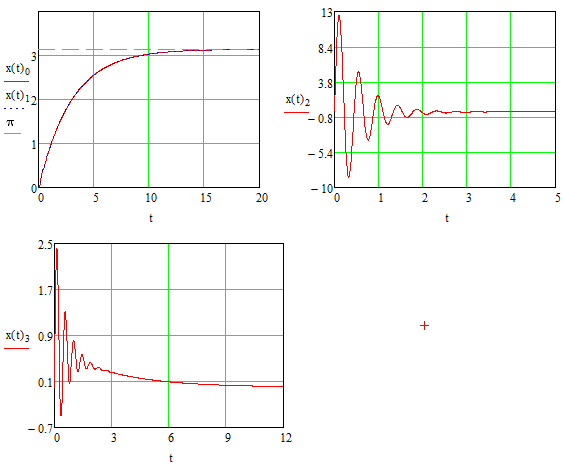 На рисунке 29 представлены графики угла поворота ротора двигателя и выходного вала редуктора, график движущего момента и график управляющего сигнала для 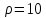 и коэффициентов и коэффициентов 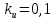 ; ; 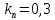 Рис 29 – Графики 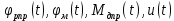 для для 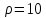 Исходя из анализа графиков можно заметить, что графики движущего момента и управляющего сигнала имеют небольшие значения и достаточно быстро затухают, также ошибка по углу достаточно быстро стремится к нулю. Исследовав графики 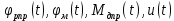 при разных при разных 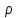 , было принято решение, что точка с оптимальными коэффициентами имеет весовой множитель 10 и коэффициенты , было принято решение, что точка с оптимальными коэффициентами имеет весовой множитель 10 и коэффициенты 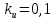 ; ; 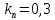 . .4.5. Описание наилучшего переходного процесса. С учётом принятых ограничений: устойчивость, 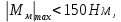 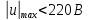 , ,А  также нежелательности превышения ошибки  получена оптимальная точка в пространстве коэффициентов обратной связи ( получена оптимальная точка в пространстве коэффициентов обратной связи (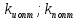 ). Необходимо для неё построить графики ). Необходимо для неё построить графики 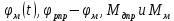 на одном рисунке, а также график управляющего сигнала u. Такие же графики надо построить для точки с на одном рисунке, а также график управляющего сигнала u. Такие же графики надо построить для точки с 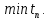 Р 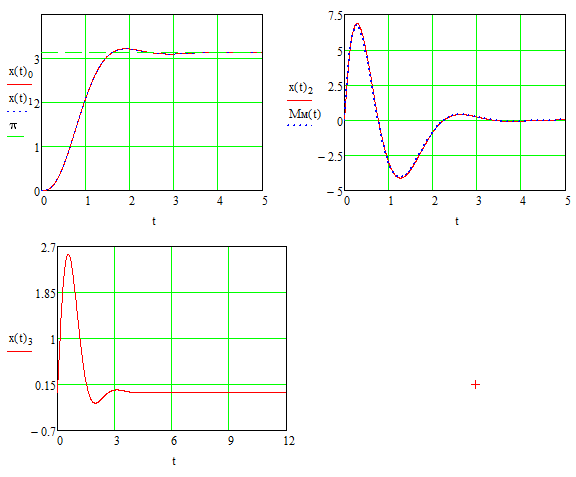 ис 30 – Графики 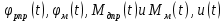 коэффициенты коэффициенты 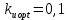 ; ; 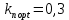 . .Рис 31 – Графики 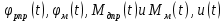 коэффициенты коэффициенты  ; ;  . .Исходя из анализа графиков для оптимальных коэффициентов и коэффициентов, при которых наступает минимальная длительность можно сделать вывод, что наиболее оптимальная точка это точка с наименьшей длительностью. Если смотреть на график моментов, то амплитуда момента при  меньше, чем при оптимальных коэффициентах, а затухание происходит примерно за одно и то же время. Говоря об управляющем сигнале, амплитуда в обоих случаях одинаковая, но скорость затухания выше при меньше, чем при оптимальных коэффициентах, а затухание происходит примерно за одно и то же время. Говоря об управляющем сигнале, амплитуда в обоих случаях одинаковая, но скорость затухания выше при  . Также, ошибка угла поворота гораздо быстрее обнуляется при . Также, ошибка угла поворота гораздо быстрее обнуляется при  . Из всего перечисленного следует, что коэффициенты при . Из всего перечисленного следует, что коэффициенты при  будут наиболее оптимальны в представленной работе, судя по графикам, система не является ни резкой, ни вялой, она оптимальна. будут наиболее оптимальны в представленной работе, судя по графикам, система не является ни резкой, ни вялой, она оптимальна.Вывод В данной курсовой работе: Была сформирована система уравнений движения механизма, по этим уравнениям составлена структурная схема, далее следовала проверка на устойчивость с помощью критерия Стодолы и Раусса-Гурвица, а также с помощью годографа Михайлова, далее исследовалось, как изменяются переходных процессы в зависимости от коэффициентов  и и  как в области устойчивости, так и вне области, также были найдены области допустимых значений момента и управляющего сигнала, построены линии равных длительностей и линии равных уровней интегрального показателя качества для трёх разных весовых множителей, найдены оптимальные коэффициенты. Хотелось бы добавить, что данная курсовая работа послужила очень интересным дополнением к теоретической части, что была получена ранее, стало более понятно, какие области устойчивости бывают, какой формы и размеров, стало ясно как именно и из каких соображений нужно подбирать коэффициенты ПИ-регулятора, что они не только должны быть не большими, но и удовлетворять условиям. Интересная особенность, что в области устойчивость есть линии уровня и эта линия разделяет область на две части, часть с значением меньшим, чем у линии уровня и часть со значением большим. Наиболее долгим оказался перебор коэффициентов как в области устойчивости, так и вне области, также были найдены области допустимых значений момента и управляющего сигнала, построены линии равных длительностей и линии равных уровней интегрального показателя качества для трёх разных весовых множителей, найдены оптимальные коэффициенты. Хотелось бы добавить, что данная курсовая работа послужила очень интересным дополнением к теоретической части, что была получена ранее, стало более понятно, какие области устойчивости бывают, какой формы и размеров, стало ясно как именно и из каких соображений нужно подбирать коэффициенты ПИ-регулятора, что они не только должны быть не большими, но и удовлетворять условиям. Интересная особенность, что в области устойчивость есть линии уровня и эта линия разделяет область на две части, часть с значением меньшим, чем у линии уровня и часть со значением большим. Наиболее долгим оказался перебор коэффициентов  и и  при построении линий уровня и оптимальной кривой. Итогом работы стало нахождения оптимальных коэффициентов для оптимального управления системой. при построении линий уровня и оптимальной кривой. Итогом работы стало нахождения оптимальных коэффициентов для оптимального управления системой. |