Теория телетрафика. Курсовой проект по дисциплине Теория телетрафика
 Скачать 288.46 Kb. Скачать 288.46 Kb.
|
|
Федеральное агентство связи Государственное образовательное учреждение высшего профессионального образования «Сибирский государственный университет телекоммуникаций и информатики» Кафедра АЭС Курсовой проект по дисциплине «Теория телетрафика» Выполнил: студент группы ЗС № зачетной книжки 075 Проверил: доцент, к.т.н. Быков Ю.П. Новосибирск 2013 Задача 1 На коммутационную систему поступает поток вызовов, создающий нагрузку Y, Эрл. Определить вероятность поступления ровно i-вызовов при примитивном потоке от N источников. Вероятность поступления при простейшем потоке вызовов. Построить кривые распределения вероятностей при Рi=f (i) и произвести сравнение полученных результатов. Дано: Y=3,2 Эрл. N=8 . Рi=? Решение: Простейший поток 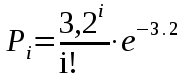 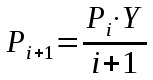 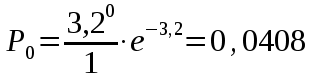 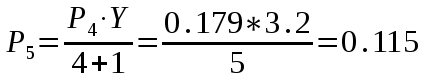 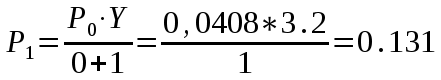 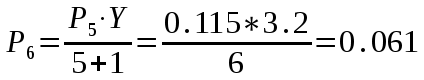 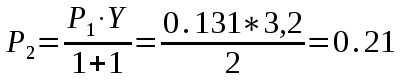 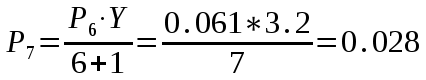 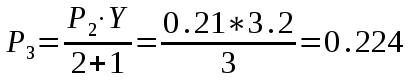 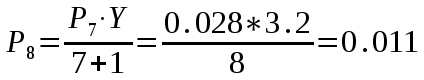 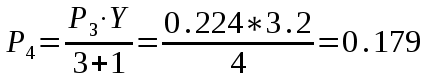 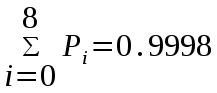 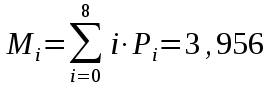 Примитивный поток 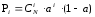 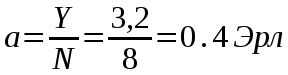 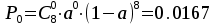 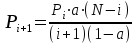 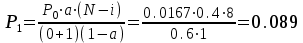 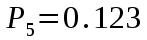 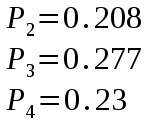 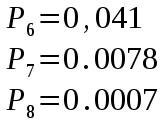 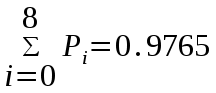 Кривые распределения вероятностей 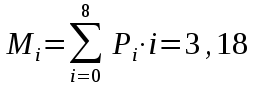 Рi i 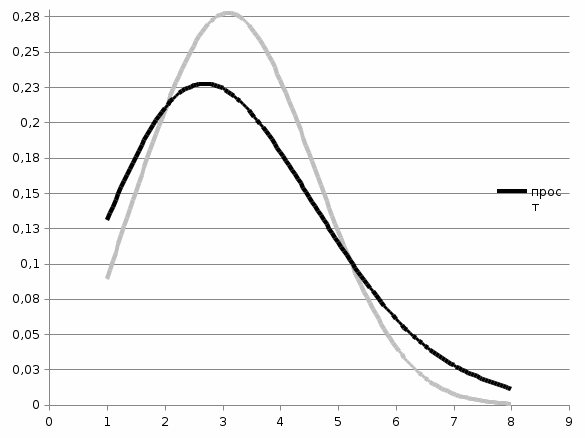 Вывод: 1. Сумма всех вероятностей приблизительно равна 1. 2. На интервале от [0;2) Рпрост>Рпримит ; (2;5) – Рпрост<Рпримит ; (5;8] - Рпрост>Рпримит. 3. Интенсивность поступающей нагрузки, выраженная в Эрл. количественно совпадает со средним числом вызовов, поступающим на единичном интервале. 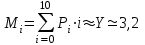 Задача 2 Пучок ИШК координатной станции АТСК-У обслуживает абонентов одного блока Аи. Определить поступающую на этот пучок нагрузку Y, если число абонентов N=1000, среднее число вызовов от одного абонента С=2,6 вызов/час, среднее время разговора Т=120 с. Доля вызовов закончившихся разговором Рр=0.6 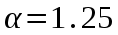 , коэффициент, который определяется по графику [1] , коэффициент, который определяется по графику [1]n=6 – нумерация на сети 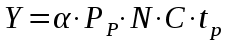 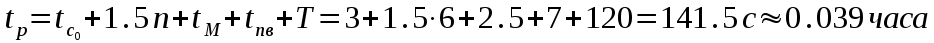 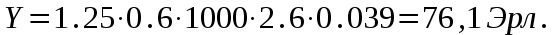 Вывод: таким образом поступающая нагрузка на абонентский блок составляет 76,1 Эрл. 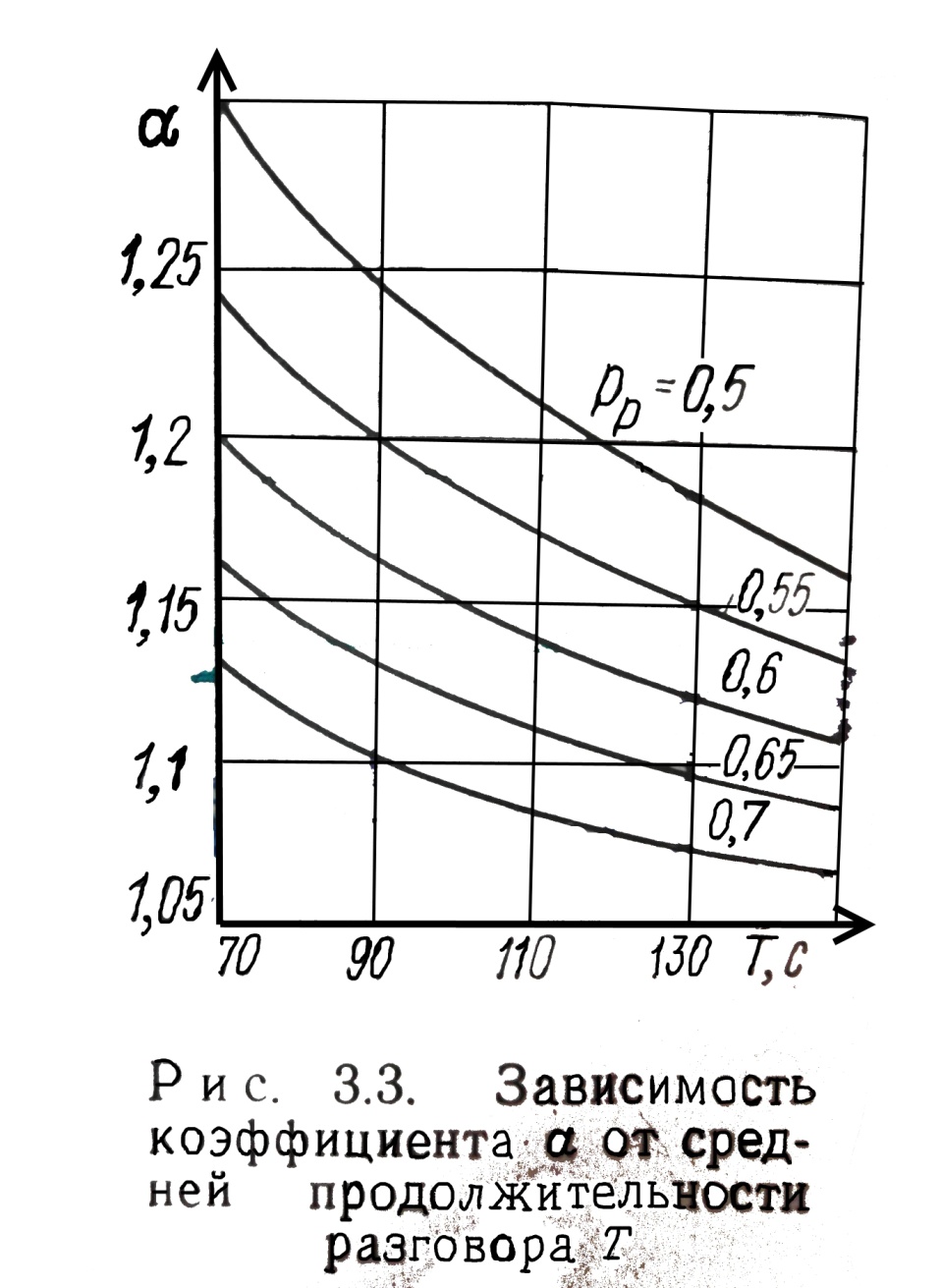 Задача 3 Задача 3Полнодоступный пучок из V=9 линий обслуживает поток вызовов. Определить пропускную способность пучка, т.е нагрузку Y, которая может поступать на этот пучок при заданной величине потерь по вызовам Рв=2% в случае простейшего потока и примитивного потока N1=50 и N2=40 источников. Простейший поток на входе определяется по 1-ой формуле Эрланга: Y0=2,9 Эрл Примитивный поток определяется по формуле Энгсета: a = 0,06 Y1 = 0,06*50 = 3 Эрл а = 0,08 Y2 = 0,08*40 = 3,2 Эрл Вывод: Y1, Y2 > Y0, следовательно примитивный поток обслуживать лучше чем простейший. Задача 4 На коммутационный блок координатной станции типа АТСК поступает простейший поток вызовов, который создает нагрузку Yб = 20 Эрл, при средней длительности занятия входа tб = 80с. Блок обслуживается одним маркером, работающим в режиме с условными потерями при постоянной длительности занятия tм = 0,8с. Блок обслуживается одним маркером, работающим в режиме с условными потерями при постоянной длительности занятия tд = 1,6с. t = tд / tм t = 2c Yм = (tм/tб)*Yб Yм = 0,2 Эрл P(y>t) = 0,0004 – Функция распределения времени задержки Из 10000 поступивших вызовов 4 будут задержаны на время больше чем 2 единицы, а остальные 9996 будут задержаны на время меньше чем 2с. Среднее время задержки для любого поступившего вызова определяется как: М[γ] = Yм/2*(1-Yм) М[γ] = 0,125 М’[γ] = М[γ] * tм М’[γ] = 0,1 c М[γз] = 1/ 2*(1-Yм) М[γз] = 0,625 М’[γз] = М[γз]*tм М’[γз] = 0,5с Задача 5 На вход ступени ГИ АТС поступает нагрузка по двум пучкам линий, математическое ожидание которой Y1 = 25 Эрл и Y2 = 50 Эрл. На выходе ступени объединенная нагрузка распределяется по направлениям пропорционально коэффициентам K1 = 0,1; К2 = 0,25; К3 = 0,3; К4 = 0,35. Определить расчетное значение нагрузки каждого направления и относительное отклонение расчетного значения нагрузки от ее математического ожидания. Общая нагрузка Y = Y1+ Y2 Y = 75 Эрл Y’i= Y*Ki Y’1 = 75*0,1 = 7,5 Эрл Y’2 = 75*0,25 = 18,75 Эрл Y’3 = 75*0,3 = 22,5 Эрл Y’4 = 75*0,35 = 26,25 Эрл YPi = Y’i +0,6742√Y’i YP1 = 7,5+1,846 = 9,346 Эрл YP2 = 18,75 +2,919 = 21,669 Эрл YP3 = 22,5 + 3,198 = 25,698 Эрл YP4 = 26,25 + 3,454 = 29,704 Эрл 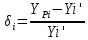 δ1 = 9,346 – 7,5 = 1,846 Эрл δ2 = 21,669 – 18,75 = 2,919 Эрл δ3 = 25,698 – 22,5 = 3,198 Эрл δ4 = 29,704 – 26,25 = 3,454 Эрл Вывод: чем больше нагрузка, тем меньше относительное отклонение от расчетной, потому что от ее величины зависит мера ее колеблеемости. Т.е надо стремится к обслуживанию большой нагрузки, и укрупнять пучки каналов. |
