Решение систем линейных алгебраических уравнений. Приходько Д.С.__лаб1__вариант №17_rev__1. Лабораторная работа 1 по дисциплине Программирование студент фдо тусур приходько Д. С. группа з421П55
 Скачать 1.33 Mb. Скачать 1.33 Mb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР) Факультет дистанционного обучения Кафедра АОИ Лабораторная работа № 1 по дисциплине «Программирование» Выполнил: студент ФДО ТУСУР Приходько Д.С. группа з-421П5-5 Томск 2021 Индивидуальный вариант №17: Задание № 1. Решение систем линейных алгебраических уравнений методом Гаусса 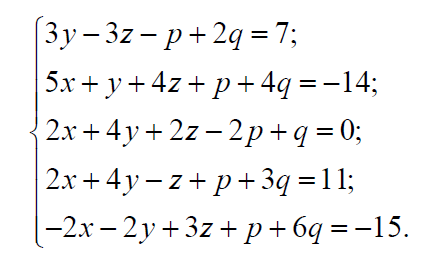 Описание реализуемого метода Метод преобразований Гаусса (также известный как преобразование методом последовательного исключения неизвестных переменных из уравнения или матрицы) для решения систем линейных уравнений представляет собой классический метод решения системы алгебраических уравнений (СЛАУ). Также этот классический метод используют для решения таких задач, как получение обратных матриц и определения ранга матрицы. Преобразование с помощью метода Гаусса заключается в совершении небольших (элементарных) последовательных изменениях системы линейных алгебраических уравнений, приводящих к исключению переменных из неё сверху вниз с образованием новой треугольной системы уравнений, являющейся равносильной исходной. Такое решение носит название прямого хода решения Гаусса, так как весь процесс осуществляется сверху вниз. После приведения исходной системы уравнений к треугольной осуществляется нахождение всех переменных системы снизу вверх (то есть первые найденные переменные занимают находятся именно на последних строчках системы или матрицы). Эта часть решения известна также как обратный ход решения методом Гаусса. Заключается его алгоритм в следующем: сначала вычисляется переменные, находящиеся ближе всего к низу системы уравнений или матрицы, затем полученные значения подставляются выше и таким образом находится ещё одна переменная и так далее. Последовательность действий для общего решения системы уравнения методом Гаусса заключается в поочередном применении прямого и обратного хода к матрице на основе СЛАУ. Пусть исходная система уравнений имеет следующий вид: 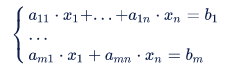 Чтобы решить СЛАУ методом Гаусса, необходимо записать исходную систему уравнений в виде матрицы: 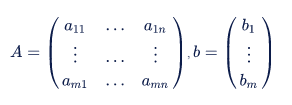 Матрица A называется основной матрицей и представляет собой записанные по порядку коэффициенты при переменных, а b называется столбцом её свободных членов. Матрица A , записанная через черту со столбцом свободных членов называется расширенной матрицей:  Теперь необходимо с помощью элементарных преобразований над системой уравнений (или над матрицей, так как это удобнее) привести её к следующему виду: 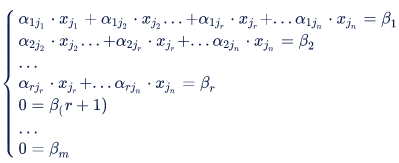 Матрица, полученная из коэффициентов преобразованной системы уравнения называется ступенчатой, вот так обычно выглядят ступенчатые матрицы:  Для этих матриц характерен следующий набор свойств: Все её нулевые строки стоят после ненулевых; Если некоторая строка матрицы с номером k ненулевая, то в предыдущей строчке этой же матрицы нулей меньше, чем в этой, обладающей номером k; После получения ступенчатой матрицы необходимо подставить полученные переменные в оставшиеся уравнения (начиная с конца) и получить оставшиеся значения переменных. При упрощении матрицы или системы уравнений этим методом нужно использовать только элементарные преобразования. Таким преобразованиями считаются операции, которые возможно применять к матрице или системе уравнений без изменения её смысла: перестановка нескольких строк местами; прибавление или вычитание из одной строчки матрицы другой строчки из неё же; умножение или деление строчки на константу, не равную нулю; строчку, состоящую из одних нулей, полученную в процессе вычисления и упрощения системы, нужно удалить; также нужно удалить лишние пропорциональные строчки, выбрав для системы единственную из них с более подходящими и удобными для дальнейших вычислений коэффициентами; Все элементарные преобразования являются обратимыми. Различают три возникающих случая при использовании метода Гаусса для решения систем: Когда система несовместная, то есть у неё нет каких-либо решений; У системы уравнений есть решение, причём единственное, а количество ненулевых строк и столбцов в матрице равно между собой; Система имеет некое количество или множество возможных решений, а количество строк в ней меньше чем количество столбцов; Текст программы: #include #include #include #include void showVector(int n, double * vec); void forwardStroke(int n, double **matrixA, double *vectorB); void returnStroke(int n, double **matrixA, double *vectorB, double *vectorX); int main() { system("chcp 1251"); int i,j,n; double **matrixA, *vectorB, *vectorX; do { printf("Введите количество уравнений: "); scanf("%d",&n); //Выделяем память под матрицу А и векторы В и Х matrixA = (double **)malloc(n*sizeof(double)); vectorB = (double *)malloc(n*sizeof(double)); vectorX = (double *)malloc(n*sizeof(double)); for(i = 0; i < n; i++) { matrixA[i] = (double *)malloc(n*sizeof(double)); //Ввод матрицы A (matrixA) for(j = 0; j < n; j++) { printf("a[%d][%d] = ",i + 1,j + 1); scanf("%lf",&matrixA[i][j]); } } //Ввод столбца свободных членов (vectorB) for(i = 0; i < n; i++) { printf("b[%d] = ",i + 1); scanf("%lf",&vectorB[i]); } printf("\tВведённые данные\r\n"); printf("Матрица A:\r\n"); for(i = 0; i < n; i++) showVector(n, matrixA[i]); printf("Столбец свободных членов:\r\n"); showVector(n, vectorB); printf("\tРешение СЛАУ методом Гаусса\r\n"); forwardStroke(n, matrixA, vectorB); printf("Прямой ход\r\n");//Прямой ход printf("Матрица А:\r\n"); for(i = 0; i < n; i++) showVector(n, matrixA[i]); printf("Столбец свободных членов:\r\n"); showVector(n, vectorB); returnStroke(n, matrixA, vectorB, vectorX); printf("Обратный ход\r\n");//Обратный ход printf("Матрица А:\r\n"); for(i = 0; i < n; i++) showVector(n, matrixA[i]); printf("Столбец свободных членов:\r\n"); showVector(n, vectorB); printf("Результат :\r\n"); showVector(n, vectorX); //Чистим память free((void *)matrixA); free((void *)vectorB); free((void *)vectorX); } } void showVector(int n, double * vec) { for(int i = 0; i < n; i++) printf("%.3f ",vec[i]); printf("\r\n"); } void forwardStroke(int n, double **matrixA, double *vectorB) { double v; for(int k = 0,i,j,im; k < n - 1; k++) { im = k; for(i = k + 1; i < n; i++) { if(fabs(matrixA[im][k]) < fabs(matrixA[i][k])) { im = i; } } if(im != k) { for(j = 0; j < n; j++) { v = matrixA[im][j]; matrixA[im][j] = matrixA[k][j]; matrixA[k][j] = v; } v = vectorB[im]; vectorB[im] = vectorB[k]; vectorB[k] = v; } for(i = k + 1; i < n; i++) { v = 1.0*matrixA[i][k]/matrixA[k][k]; matrixA[i][k] = 0; vectorB[i] = vectorB[i] - v*vectorB[k]; if(v != 0) for(j = k + 1; j < n; j++) { matrixA[i][j] = matrixA[i][j] - v*matrixA[k][j]; } } } } void returnStroke(int n, double **matrixA, double *vectorB, double *vectorX) { double s = 0; vectorX[n - 1] = 1.0*vectorB[n - 1]/matrixA[n - 1][n - 1]; for(int i = n - 2, j; 0 <= i; i--) { s = 0; for(j = i + 1; j < n; j++) { s = s+matrixA[i][j]*vectorX[j]; } vectorX[i] = 1.0*(vectorB[i] - s)/matrixA[i][i]; } } Результаты тестирования программы: 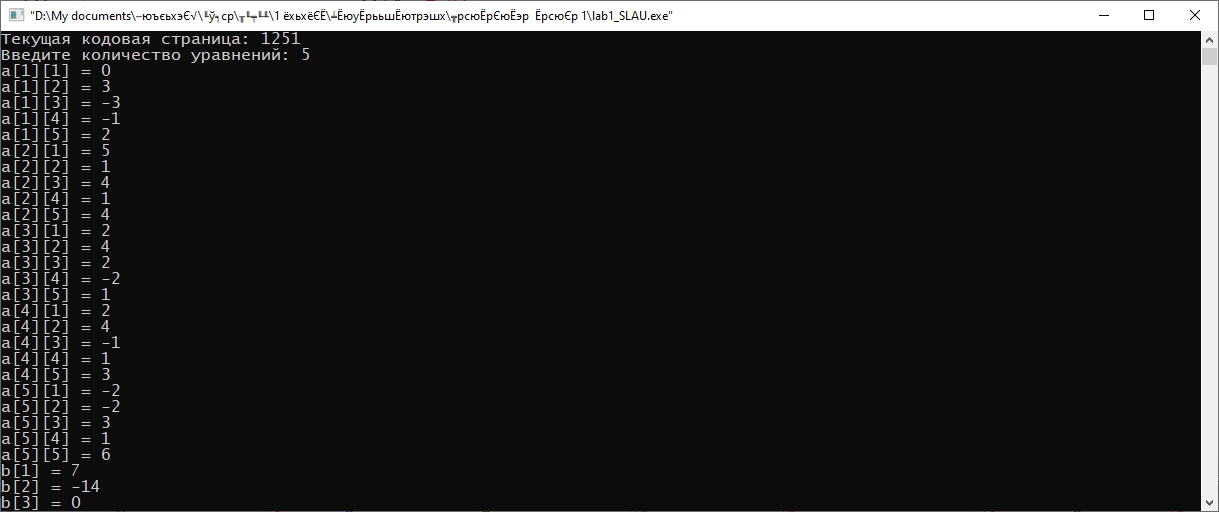 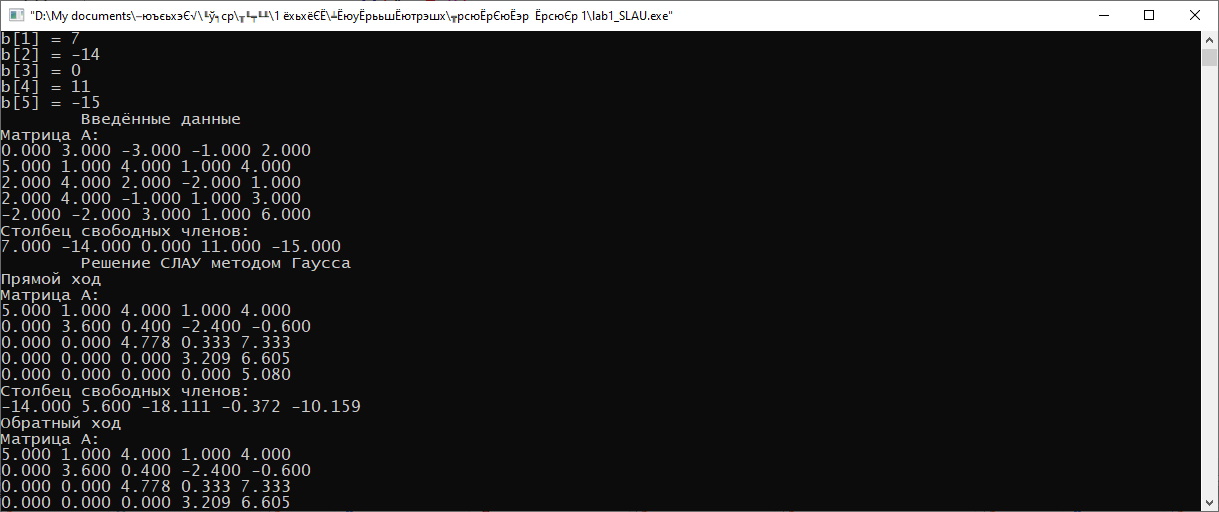 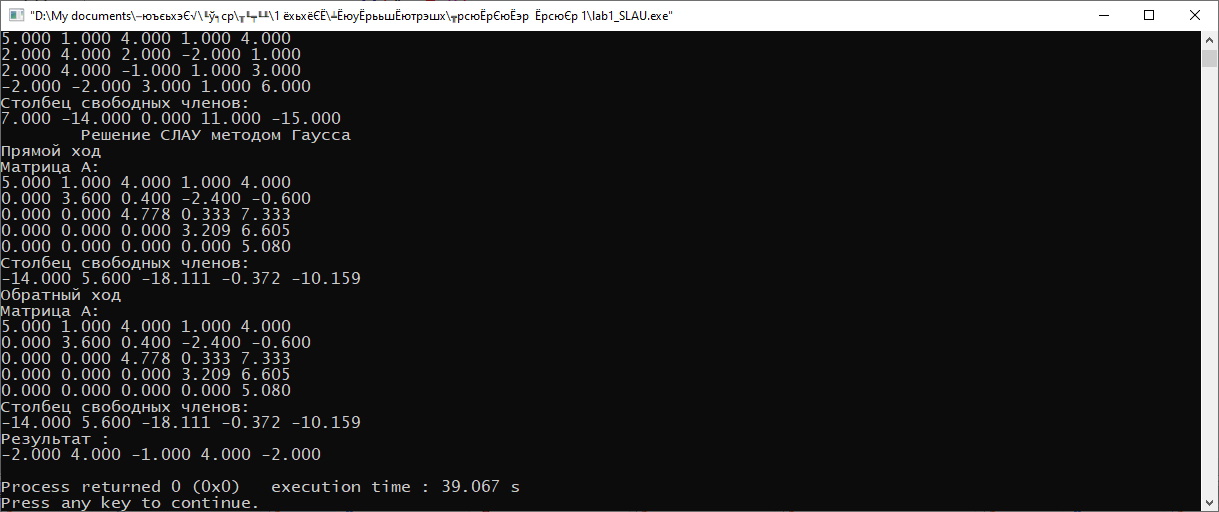 Индивидуальный вариант №17: Задание № 2. Численное интегрирование методом Симпсона. Вычислить определенный интеграл от функции 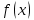 на промежутке [a, b] методом Симпсона. на промежутке [a, b] методом Симпсона. 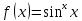 , a=-5, b=-4; , a=-5, b=-4;Число разбиений n = 10; 20; 60; 100. Описание реализуемого метода Метод Cимпсона можно интерпретировать как квадратурную формулу, в которой 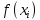 интерполируется кусочно-квадратичными функциями (параболами). Пусть отрезок [a, b] разбит на сегменты [ интерполируется кусочно-квадратичными функциями (параболами). Пусть отрезок [a, b] разбит на сегменты [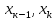 ] с длиной ] с длиной 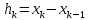 , , 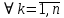 (рисунок 1а). При этом (рисунок 1а). При этом 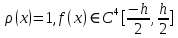 . .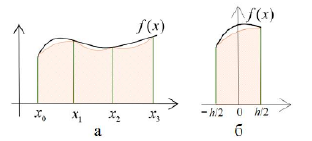 Рисунок 1. Кусочно-квадратичное интерполирование (а) и локальный сегмент длины h (б). Путём замены переменных отрезок 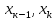 приводится к эталонному отрезку приводится к эталонному отрезку 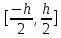 , как показано на рисунке 1б. Восстановим уравнение параболы, которая аппроксимирует функцию , как показано на рисунке 1б. Восстановим уравнение параболы, которая аппроксимирует функцию 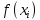 . Пусть . Пусть 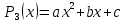 , тогда , тогда 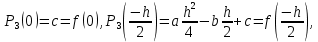 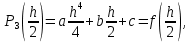 откуда 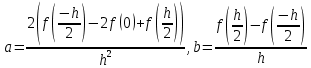 Каноническая формула метода парабол имеет вид: 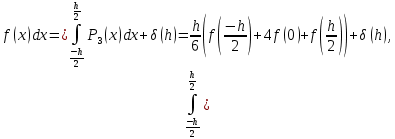 где 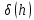 - остаточный член (погрешность аппроксимации) - остаточный член (погрешность аппроксимации)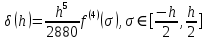 В сумме по всем сегментам получим общую квадратурную формулу метода парабол (метод Симпсона): 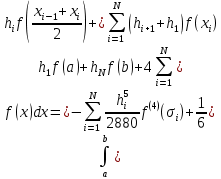 , ,где 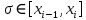 Квадратурная формула парабол (метод Симпсона) имеет третий порядок точности и четвёртый порядок аппроксимации. Текст программы: #include #include #include //Подынтегральная функция float Fx(float x) { float result = pow(sin(x), x); printf("x = %f, %f\n", x, result); return result; } float simpson(float a, float b, int n) { system("chcp 1251"); //Границы интервалов интегрирования a = -5; b = -4; //h - шаг интегрирования, h2 - полушаг интегрирования, x - текущее значение переменной интегрирования. float h, h2, x, s; printf("Введите число разбиений (10, 20, 60 или 100) n = ", &n); scanf("%d", &n); //определение шагов интегрирования h = (b - a) / n; printf("h = %f\n", h); //Определение полушага интегрирования h2 = h / 2; printf("h2 = %f\n", h2); x = a; //текущее значение переменной интегрирования s=(Fx(a)+Fx(b))/2+2*Fx(a + h2); for(int i=1; i<=n-1; i++) { x=x+h; s=s+Fx(x)+Fx(x+h2); } return s*h/3; } float main(float x) { printf("\nИнтеграл = %f\n", simpson(0.0f, 2.0f, 200)); return 0; } Результаты тестирования программы: Число разбиений n=10 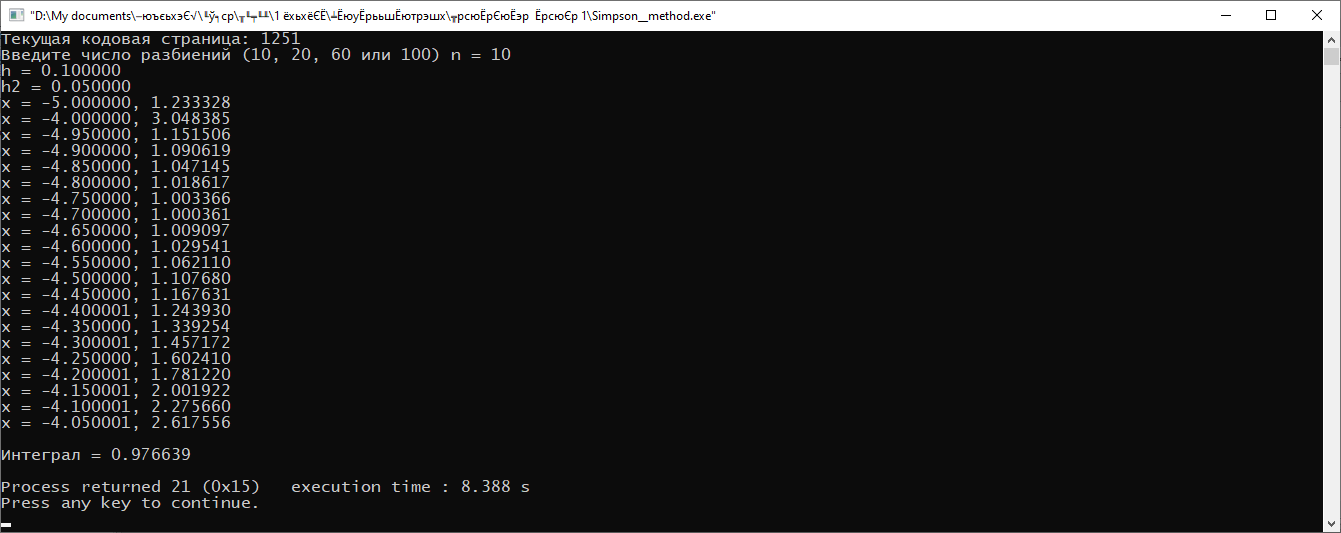 Число разбиений n=20 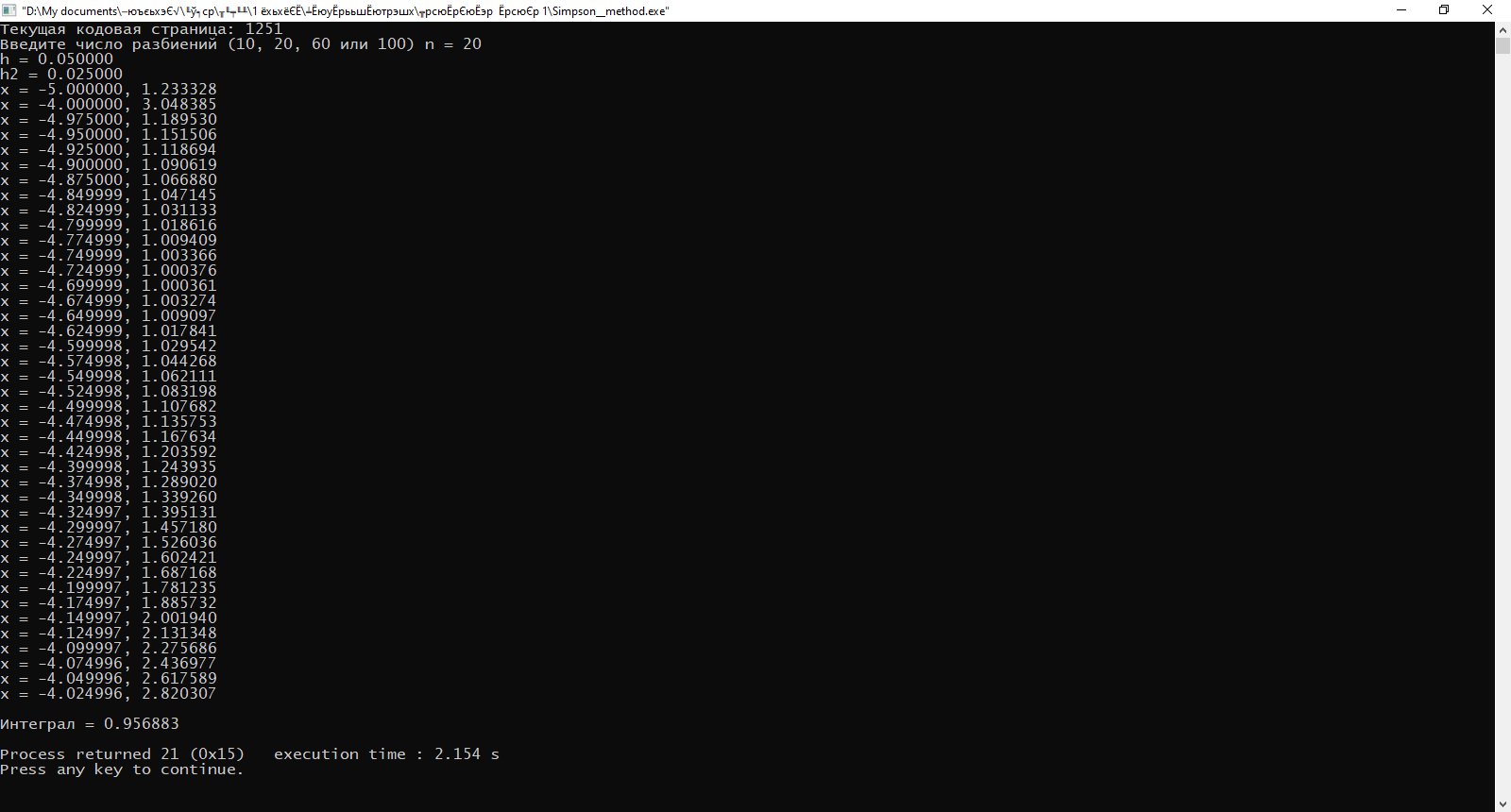 Число разбиений n=60 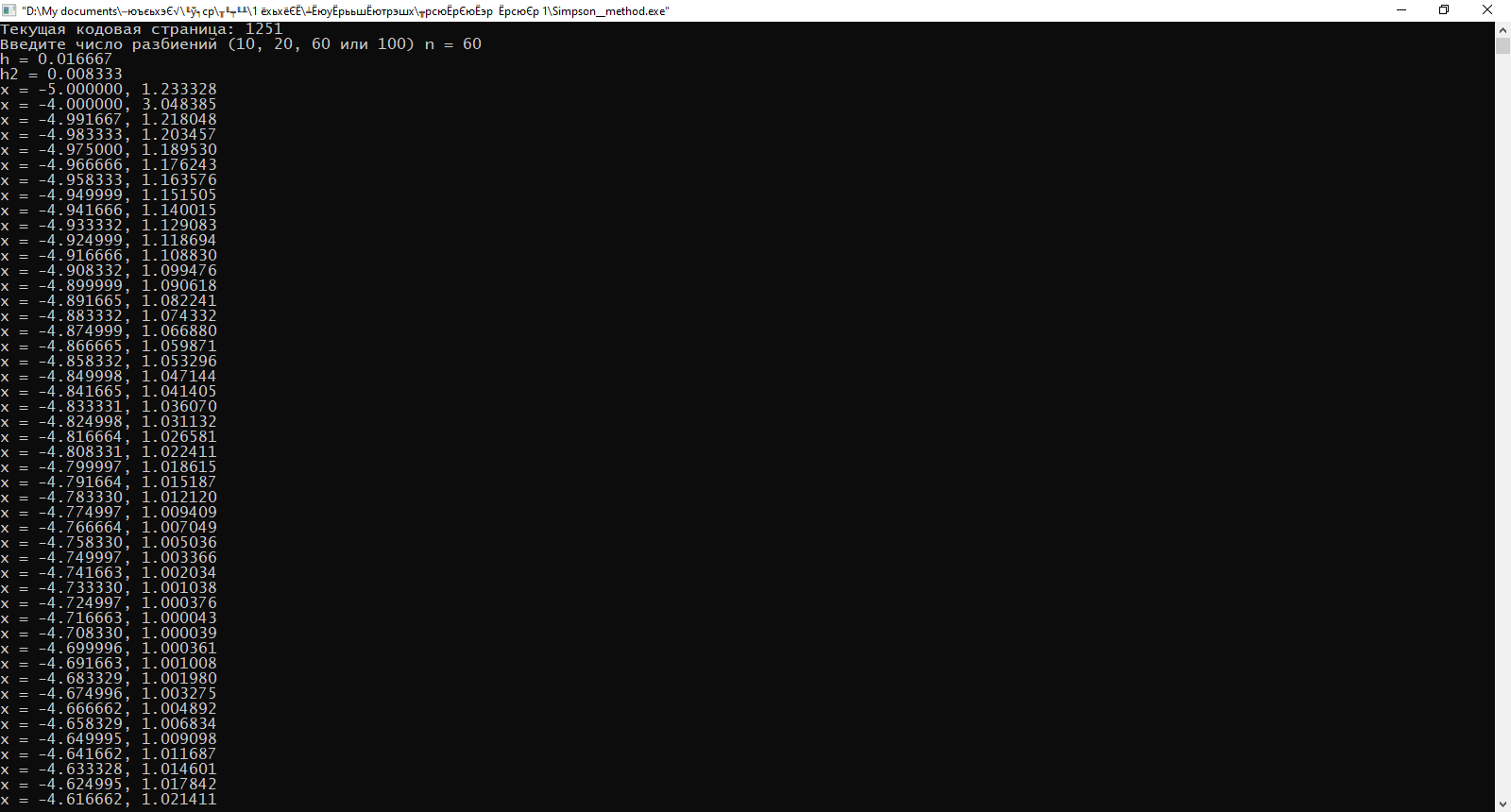  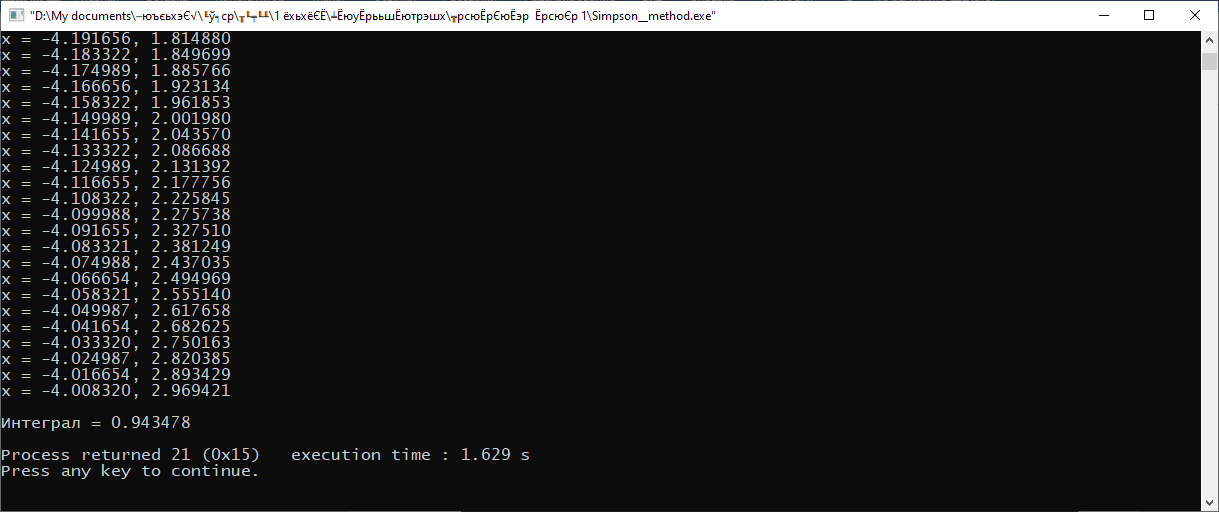 Число разбиений n=100 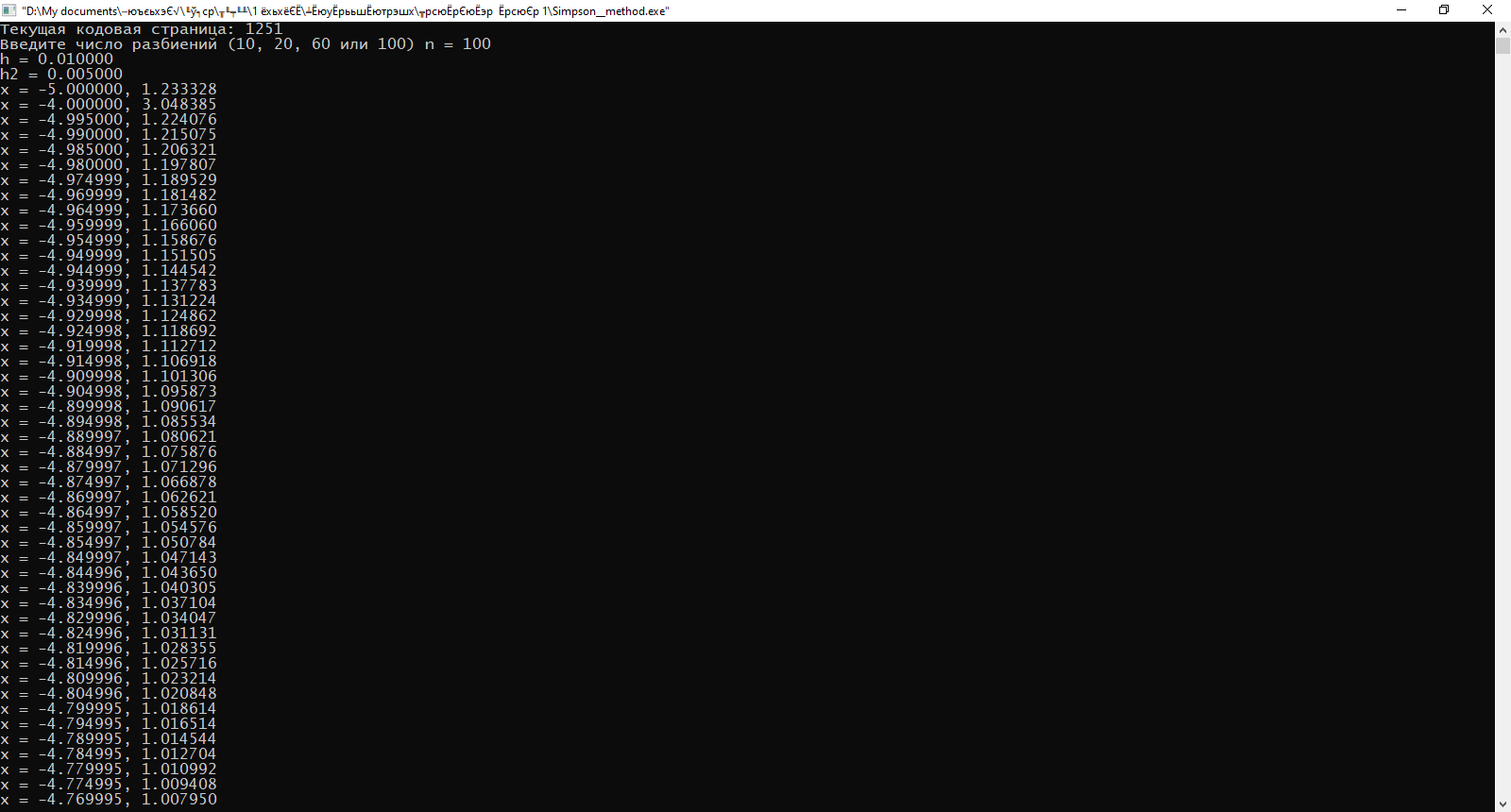    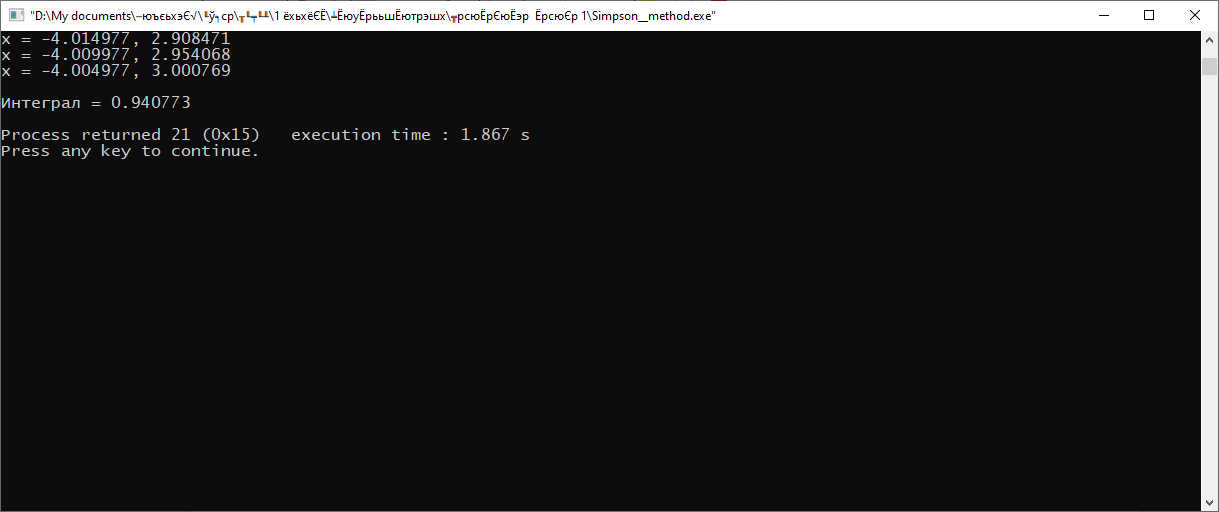 |
