Математическое моделирование. Лабораторная работа 1. Математическое моделирование.. Лабораторная работа 1. Тему Определение параметров регрессионной модели по экспериментальным данным методом наименьших квадратов
 Скачать 236.5 Kb. Скачать 236.5 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «КУЗБАССКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ Т.Ф.ГОРБАЧЕВА» Кафедра «технологии машиностроения» ЛАБОРАТОРНАЯ РАБОТА №1. ТЕМУ: «Определение параметров регрессионной модели по экспериментальным данным методом наименьших квадратов» по дисциплине: Технологическое обеспечение качества Выполнил студент гр.КТмз221 Осенний М.С. Проверил преподаватель: Абабков Н.В. г. Кемерово – 2023 Вариант 8 Определить зависимость относительного удлинение сплава В95 от времени искусственного старения, используя данные:  Рис. 1. Исходные данные 1. Для оформления решения составим таблицу в ППП Microsoft Office Excel (рис. 2) и, исходя из задания, занесем экспериментальные данные в ячейки A3:B12. 2. Построим точечный график по диапазону ячеек A3:B12. Далее используем команду Добавить линию тренда  Рис. 2 Таблица данных объекта и модели В диалоговом окне Линия тренда выберем параметр Линейная. На вкладке Параметры установим флажки Показывать уравнение на диаграмме и Поместить на диаграмму величину достоверности аппроксимации (R^2) Результат выполнения команды Линия тренда представлен на (рис. 3). 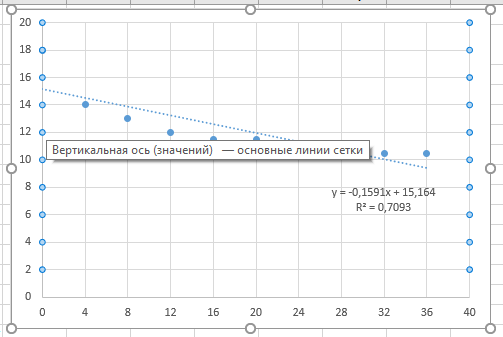 Рис. 3. График линии тренда линейной модели 3. По приведенному выше алгоритму выполним регрессионный анализ для нелинейных моделей, в частности построим полиномиальную модель второго порядка, последовательно увеличить порядок уравнения до шестого. 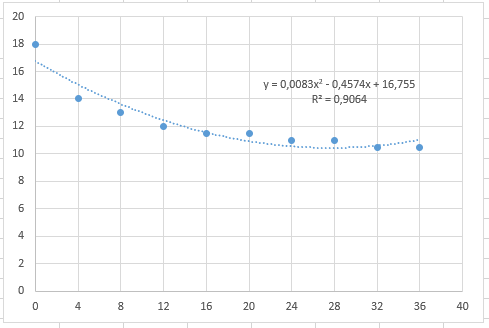 Рис. 4 Полиномиальный тренд 2-го порядка  Рис. 5 Полиномиальный тренд 3-го порядка  Рис. 6 Полиномиальный тренд 4-го порядка  Рис. 7 Полиномиальный тренд 5-го порядка 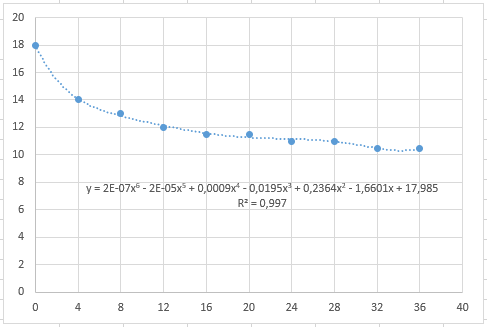 Рис. 8 Полиномиальный тренд 6-го порядка 4. В данном случае целесообразно выбрать полином 3го порядка. 5. Установим теоретическое значение наблюдаемой величины Y. Для этого рассчитаем теоретические значение Yв ячейке C3-С12, по формуле -0,0005x3 + 0,0353x2 - 0,8268x + 17,562 6. Вычислить ошибку модели в ячейке D3 по формуле =А3-C3 и скопируем на весь столбец D (рис. 9).  Рис. 9 Расчет теоретических значений и ошибок 7. Для проверки модели на адекватность построим гистограмму распределения ее остатков. Составим диапазон изменения остатков, определим их минимальное и максимальное значения с помощью функций МАКС() и МИН(). Затем весь диапазон изменения остатков разобьем на несколько равных поддиапазонов и рассчитаем число попаданий ошибки (остатков) в каждый поддиапазон. Все границы интервалов запишем в отдельную строку или столбец (рис. 10).  Рис. 10 Нахождение ошибки и карманов Далее для построения гистограммы распределения остатков выберем команду Сервис, Анализ данных -Гистограмма. Результаты построения приведены на рис. 11. 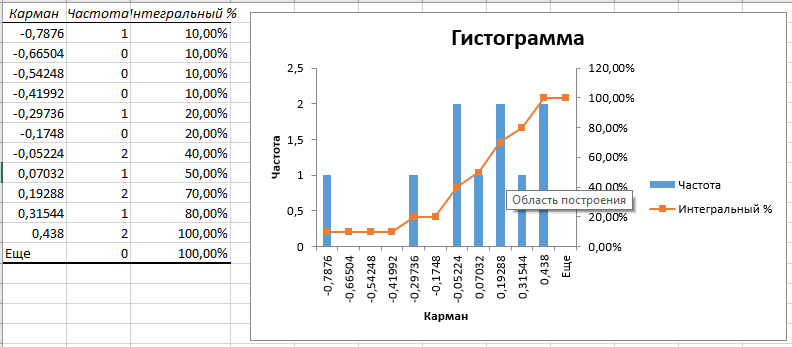 Рис. 11 Гистограмма распределения остатков 8. Для проверки модели на адекватность построим график содержательного анализа остатков модели в зависимости от входной переменной Х. Построим точечный график по диапазону ячеек в столбцах A3:A12 и D3:D12.  Рис. 12. Точечный график Таким образом, была получена зависимость предела текучести сплава от старения в виде: у=-0,0005x3 + 0,0353x2 - 0,8268x + 17,562 Высокий коэффициент R2=0,9737 указывает на хорошее качество модели. График остатков позволяет сделать вывод об адекватности построенной модели. |
