Моделирование. Решение транспортной задачи. Транспортная отчет (Готово). Лабораторная работа 2 Использование ms excel для решения транспортной задачи титульник!!!! Цели и задачи лабораторной работы
 Скачать 162.67 Kb. Скачать 162.67 Kb.
|
ЛАБОРАТОРНАЯ РАБОТА №2Использование MS Excel для решения транспортной задачиТИТУЛЬНИК!!!! 1. Цели и задачи лабораторной работыЦель работы – овладение навыками работы различных пакетов прикладных программ для решения задач нелинейного программирования. Задачи – составить математическую модель задачи определенного варианта и найти ее решение с использованием пакета MS Excel. Решение транспортной задачи с помощью функции «Поиск решения»Задание: Рассматривается следующая транспортная задача. 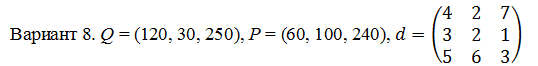
В 5-м столбце указаны мощности поставщиков, в 5-й строке - спрос потребителей. Остальные числа таблицы — это стоимость перевозки единицы груза от соответствующего поставщика к соответствующему потребителю. Таким образом, стоимость перевозки единицы груза от 3-го поставщика ко 2-му потребителю равна 1 ден.ед. Необходимо составить оптимальный план поставок при котором затраты будут минимальными. Решение Транспортная задача относится к специальным задачам линейного программирования. Общая постановка транспортной задачи состоит в определении оптимального плана перевозок некоторого однородного груза из i пунктов от- правления A₁, A₂, … Aᵢ, в j пунктов назначения B₁, B₂, … Bⱼ. При этом в качестве критерия оптимальности обычно берется либо минимальная стоимость перевозок всего груза, либо минимальное время его доставки. Рассмотрим транспортную задачу, в качестве критерия оптимальности которой взята минимальная стоимость перевозок всего груза. Обозначим через cᵢⱼ тарифы перевозки единицы груза из i-го пункта отправления в j-й пункт назначения, через aᵢ– запасы груза в i-м пункте отправления, через bⱼ– потребности в грузе в j-м пункте назначения, а через xᵢⱼ количество единиц груза, перевозимого из i-го пункта отправления в j-й пункт назначения. Тогда математическая постановка транспортной задачи состоит в определении минимального значения функции: 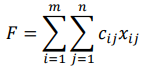 (1.1) (1.1)при условиях: 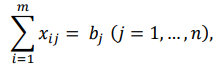 (1.2) (1.2)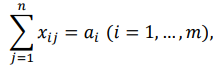 (1.3) (1.3)Функция (1.1) называется целевой функцией задачи. Поскольку переменные xᵢⱼ удовлетворяют системам линейных уравнений (1.2) и (1.3) и условию неотрицательности (1.4), обеспечиваются доставка необходимого количества груза в каждый из пунктов назначения, вывоз имеющегося груза из всех пунктов отправления, а также исключаются обратные перевозки. План X*=(x*ᵢⱼ)(i=1,2…m; j=1,2…n), при котором функция (1.1) принимает свое минимальное значение, называется оптимальным планом транспортной задачи. Если общая потребность в грузе в пунктах назначения равна запасу груза в пунктах отправления, то есть выполняется равенство (1.5), то модель такой транспортной задачи будет закрытой. Если же указанное условие не выполняется, то модель транспортной задачи называется открытой. 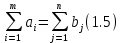 В таком случае, решение транспортной задачи при помощи MS Excel будет иметь следующий алгоритм: Занесем исходные данные в MS Excel (Рис. 1). 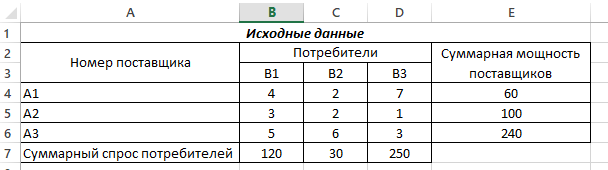 Рис. 1 – Исходные данные транспортной задачи в MS Excel Проверяем – открытая модель или закрытая. Для этого необходимо проверить выполняется ли уравнение: 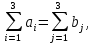 где ai - объем производства на i-м филиале (i = 1, 2, 3); bj - объем потребления j-м потребителем (j = 1, 2, 3). В нашем случае модель закрытая (120 + 30 + 250 = 60 + 100 + 240 = 400). Обозначим Xij – количество товара, перевозимое от i-го поставщика j-му потребителю (i = 1, 2, 3; j = 1, 2, 3). Выделим под переменные Xij ячейки B13:D15 (Рис. 2). 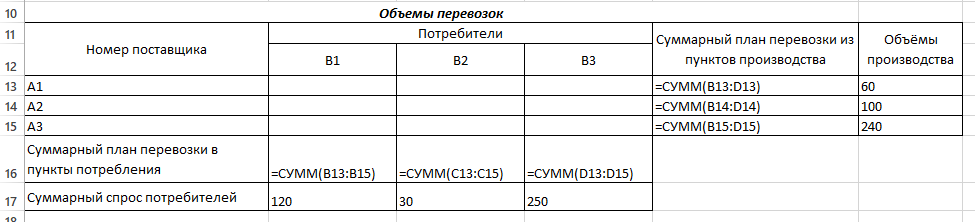 Рис. 2 – Подготовка к решению транспортной задачи В ячейках B16:D16 будем рассчитывать сумму поставок каждому потребителю. Для этого воспользуемся функцией СУММ. Аналогично в ячейках E13:E15 рассчитаем суммарные поставки каждого поставщика. В ячейку B20 запишем целевую функцию – суммарные затраты на осуществление всех поставок. 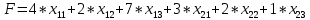 +5 +5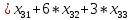 →min →minЭта функция вычисляется как сумма произведения величин поставок Xij на соответствующую им стоимость. Для этого воспользуемся функцией СУММПРОИЗВ (Рис. 3). 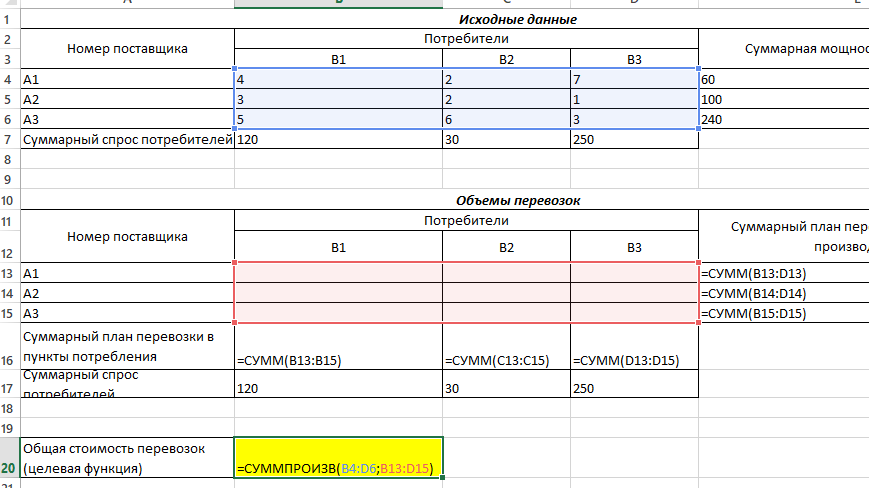 Рис. 3 – Целевая функция транспортной задачи Выделим ячейку с формулой целевой функции. Запустим надстройку «Поиск решения». В диалоговом окне в поле ввода «Установить целевую» ячейку уже содержится $В$20. Установим переключатель «Равной минимальному значению». В поле ввода «Изменяя ячейки» нужно указать величины поставок Xij, т.е. выбрать ячейки B13:D15 (Рис. 4). 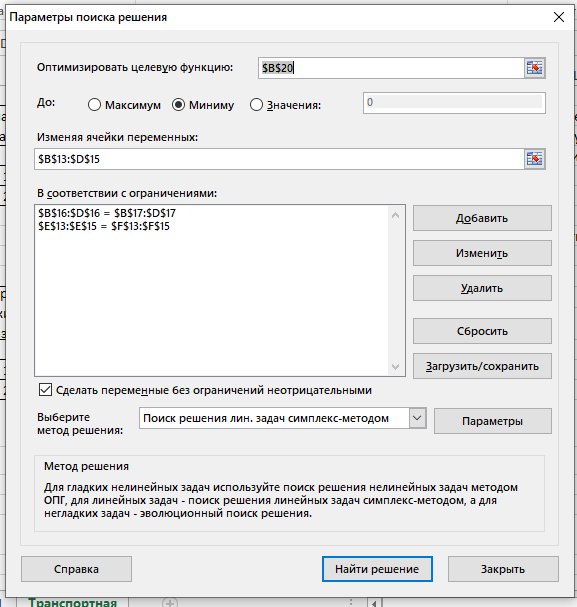 Рис. 4 – Окно «Поиск решения» Щелкаем кнопку «Добавить». И в появившееся диалоговое окно «Добавление ограничения» пропишем необходимые ограничения по суммарным спросу и мощности. Нажимаем кнопку «Выполнить». И получим необходимые значения (Рис. 5). 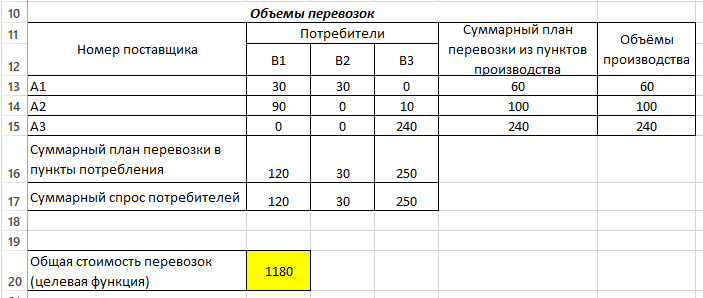 Рис. 5 – Результаты решения задачи В ячейке В20 указано 1180 ден.ед. Это минимальные затраты на перевозку. В ячейках B13:D15 указаны значения для рассчитанного оптимального плана поставок: 1-й поставщик должен доставить 30 единиц груза 1-му потребителю и 30 единиц груза 2-му потребителю. 2-й поставщик должен доставить 90 единиц груза 1-му потребителю и 10 единиц груза 3-му потребителю. 3-й поставщик должен доставить 240 единиц груза 3-му потребителю. Список литературыЛесин В.В., Лисовец Ю.П. Основы методов оптимизации: Учебное пособие. – Спб.: Издательство «Лань», 2011. – 352 с. – ISBN 978-5-8114-1217-4 Дьяконов В.П. MATLAB 7.*/R2006/R2007: Самоучитель. – М.: ДМК Пресс., 2009. – 768 с. – ISBN 978-5-94074-424-5 Сдвижков О.А. Дискретная математика и математические методы экономики с применением VBA Excel. – М.: ДМК Пресс, 2012. – 212 с. – ISBN 978-5-94074-655-3 |
