лаба4. Лабораторная работа 4 Линейные дискретные системы Дискретные сигналы и системы

• Название: Лабораторная работа 4 Линейные дискретные системы Дискретные сигналы и системы
• Анкор: лаба4
• Дата: 24.06.2022
• Размер: 217.5 Kb.
• Имя файла: lab4sci_theory.doc
• Тип: Лабораторная работа; #613120

Исследование импульсных систем с помощью среды Scilab © К. Поляков, 2016

Лабораторная работа № 4

Линейные дискретные системы

Дискретные сигналы и системы

Дискретный сигнал – это сигнал, определённый только для отдельных моментов времени, которые нумеруются целыми числами. Время 0 обозначает начало отсчёта (начальный момент времени). Для каждого момента времени с номером k (где k – целое число) значение дискретного сигнала e обозначается как e[k].

Дискретный сигнал {e[k]} – это последовательность значений e[0], e[1],e[2], …. Обычно рассматривают сигналы для неотрицательных значений k.

Рассмотрим такой сигнал (считаем, что он равен 0 при k > 6):



Его значения при k = 0, 1, 2, … (отмеченные на графике кружками) равны

e[0] = 0, e[1] = 1, e[2] = 2, e[3] = 3, e[4] = 2, e[5] = 1, e[6] = 0

В Scilab эту последовательность можно представить в виде массива

e = [0 1 2 3 2 1 0]

z-преобразование такого сигнала вычисляется по общей формуле



Поскольку при k ≥ 6 сигнал равен 0, то есть

e[6] = e[7] = e[8] = … = 0,

бесконечная сумма становится конечной:

Z{e[k]} = e[0]∙z⁰ + e[1]∙z^-1 + e[2]∙z^-2 + e[3]∙z^-3 + e[4]∙z^-4 + e[5]∙z^-5 + e[6]∙z^-6

Подставляя числовые значения e[k], получаем

Z{e[k]} = z^-1 + 2∙z^-2 + 3∙z^-3 + 2∙z^-4 + z^-5 .

Дискретная система – это система, вход и выход которой – дискретные сигналы, то есть, последовательности чисел. Входную и выходную последовательности будем обозначать соответственно как {e[k]} и {v[k]}. Буква k в квадратных скобках – это номер отсчёта или номер такта – целое число. Момент k = 0 соответствует началу наблюдений. Обычно рассматривают последовательности, которые начинаются с k = 0:

{e[k]}: e[0], e[1],e[2], …

{v[k]}: v[0], v[1],v[2], …

Линейные дискретные системы

Линейной называется система, которая обладает двумя свойствами:

1. 
   свойство суперпозиции: реакция на сумму сигналов равна сумме реакций этой системы на отдельные сигналы. Если {v₁[k]} – это реакция системы на входной сигнал {e₁[k]} и {v₂[k]} – это реакция системы на входной сигнал {e₂[k]}, то выход линейной системы при входе {e₁[k]+e₂[k]} равен {v₁[k]+ v₂[k]}.
   
2. 
   свойство однородности: умножение входного сигнала на постоянную приводит к умножению выходного сигнала на ту же постоянную. Если {v₀[k]} – это реакция системы на входной сигнал {e₀[k]}, то выход линейной системы при входе {e₀[k]} равен {v₀[k]}.
   

Обычно рассматривают стационарные системы, свойства которых не изменяются во времени. Это означает, что сдвиг во времени входного сигнала на m тактов приводит к такому же сдвигу выходного сигнала. Например, если {v₀[k]} – это реакция системы на входной сигнал {e₀[k]}, то выход линейной системы при входе {e₀[k–m]} равен {v₀[k–m]}.

На рисунке показан сдвиг во времени (запаздывание) входного и выходного сигнала на 1 такт (m = 1).



Система, для которой это свойство выполняется (при всех m) – стационарная.

Цифровой фильтр

Линейная дискретная система – это цифровой фильтр, то есть программа для обработки оцифрованного сигнала (последовательности чисел). По входной последовательности значений {e[k]} фильтр строит на выходе новую последовательность {v[k]}:



Например, линейный цифровой фильтр второго порядка вычисляет очередное значение сигнала выхода v[k] по формуле

v[k] = a₂·e[k] + a₁·e[k–1] + a₀·e[k–2] – b₁·v[k–1] – b₀·v[k–2]

Здесь a₂,a₁, a₀, b₁ и b₀ – коэффициенты фильтра; e[k] – текущее (только что полученное) значение входного сигнала; e[k–1] и e[k–2] – два предыдущих значения входного сигнала полученные соответственно в моменты k–1 и k–2; v[k–1] и v[k–2] – два предыдущих значения выходного сигнала.

Вычислим реакцию такого фильтра на единичный ступенчатый входной сигнал e[k], который равен 0 при всех k < 0 и равен 1 при всех k  0:

… = e[–2] = e[–1] = 0

e[0] = e[1] = e[2] = … = 1

Подставляя эти значения, получаем

v[0] = a₂·e[0] = a₂

v[1] = a₂·e[1] + a₁·e[0] – b₁·v[0] = a₂ + a₁ – b₁·v[0]

v[2] = a₂ +a₁ +a₀ – b₁·v[1] – b₀·v[0]

…

Так последовательно можно найти значения v[k] при всех k 0.

Рассмотрим особый случай, когда b₁ = b₀ = 0, то есть уравнение фильтра не использует прошлых значений выхода:

v[k] = a₂·e[k] + a₁·e[k–1] + a₀·e[k–2]

В этом случае получаем

v[0] = a₂, v[1] = a₂ +a₁

v[2] = a₂ +a₁ +a₀

v[3] = a₂ +a₁ +a₀

…

Это значит, что, начиная с момента k = 2, все значения сигнала выхода будут равны a₂ +a₁ +a₀, то есть переходный процесс заканчивается за конечное число шагов. Такие фильтры называются фильтрами с конечной импульсной характеристикой (КИХ-фильтрами).

Для того, чтобы в Scilab вычислить реакцию дискретной системы (цифрового фильтра) на заданный входной сигнал, используют функцию flts:

--> F = syslin('d', 0.5*%z-0.2, %z-0.5)

--> e = [0 1 2 3 2 1 0]

--> v = flts ( e, F )

Первая строка этой программы задаёт цифровой фильтр с передаточной функцией

,

во второй строке строится входной сигнал, а в третьей – с помощью функции flts вычисляется соответствующий ему выходной сигнал {v[k]}:

v = [0. 0.5 1.05 1.625 1.2125 0.70625 0.153125]

Установившееся значение

По уравнению фильтра можно определить установившееся значение выходного сигнала (если оно существует). Пусть на вход поступает единичный ступенчатый сигнал. Тогда в установившемся режиме выход не меняется, то есть должно выполняться равенство

v[k] = v[k–1] = v[k–2] = v_ = const

Поэтому, учитывая, что e[k] = e[k–1] = e[k–2] = 1, получаем

v_ = a₂ +a₁ +a₀ – b₁·v_ – b₀·v_

Отсюда сразу следует, что

.

Передаточная функция

Вернёмся снова к уравнению фильтра:

v[k] = a₂·e[k] + a₁·e[k–1] + a₀·e[k–2] – b₁·v[k–1] – b₀·v[k–2]

и запишем его в операторной форме, используя оператор запаздывания z^–1, такой что

z^–1v[k] = v[k–1], … z^–mv[k] = v[k–m].

Получаем

v[k] = a₂·e[k] + a₁·z^–1e[k] + a₀· z^–2e[k] – b₁· z^–1v[k] – b₀· z^–2v[k]

Перенесем все значения выходного сигнала в левую часть:

v[k] + b₁· z^–1v[k] + b₀· z^–2v[k] = a₂·e[k] + a₁·z^–1e[k] + a₀· z^–2e[k]

и вынесем общие множители в обеих частях:

(1 + b₁· z^–1 + b₀· z^–2) v[k] = (a₂ + a₁·z^–1 + a₀· z^–2) e[k]

Разделим обе части равенства на скобку в левой части: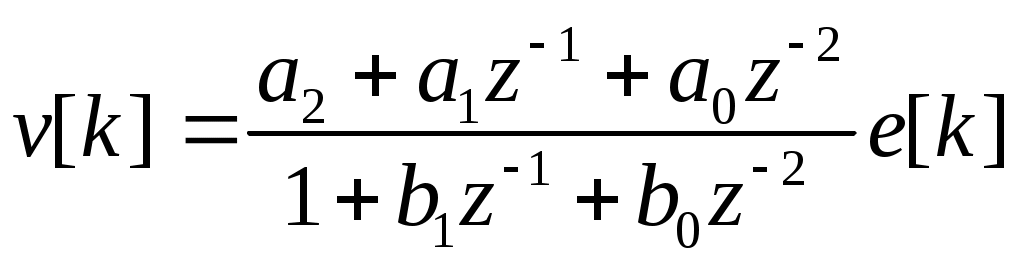

.

Умножим числитель и знаменатель на z²:



Функция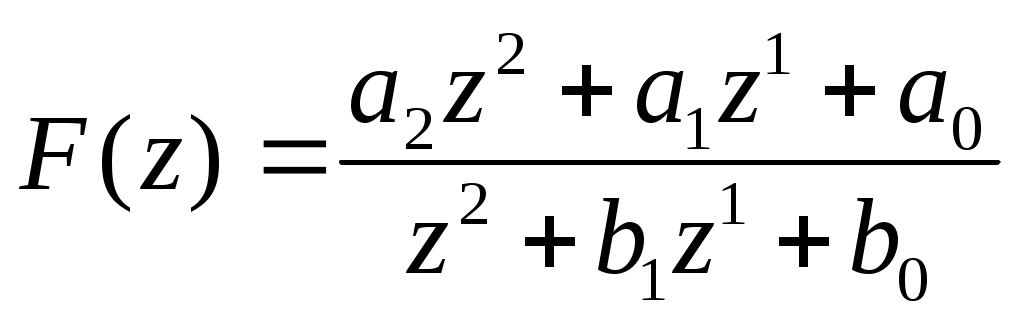



называется передаточной функцией цифрового фильтра. Для КИХ-фильтра знаменатель передаточной функции имеет вид z^N, например,

.

Заметим, что установившееся значение на выходе фильтра при единичном ступенчатом входе можно найти, подставив в передаточную функцию А(z) вместо z единицу:

.

Использование z-преобразования

Зная z-преобразование входного сигнала E(z) и передаточную функцию дискретной системы F(z), можно найти z-преобразование выходного сигнала V(z) простым умножением:

V(z) = F(z) · E(z)

Например, пусть на вход системы с передаточной функцией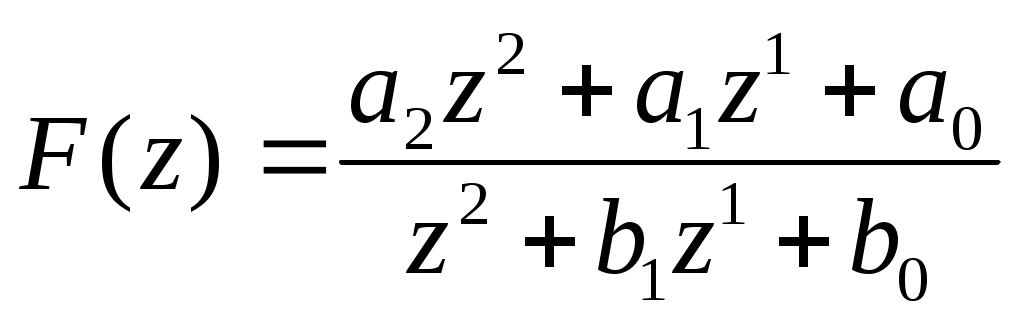



действует единичный ступенчатый входной сигнал, который имеет z-преобразование

.

Тогда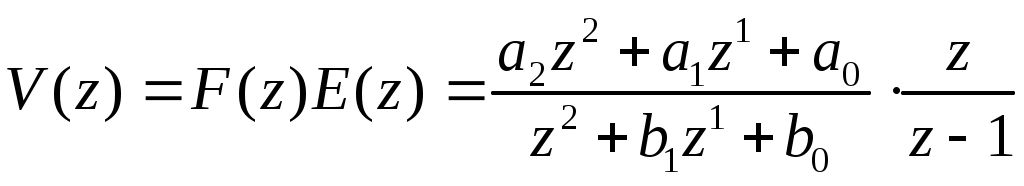

.

По теореме о начальном значении для такого изображения имеем

.

В то же время по теореме о конечном значении

.

Модели в пространстве состояний

Дискретная система может быть описана не только передаточной функцией, но и моделью в пространстве состояний:



Здесь 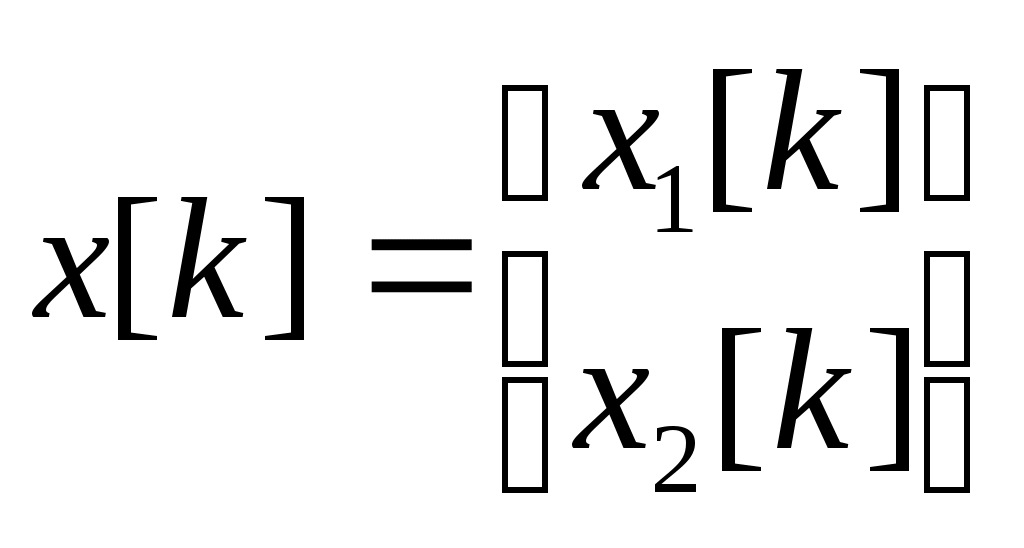– вектор состояния системы: столбец величин, которые описывают состояние системы (например, это могут быть угловая скорость и угол рыскания судна). Если вектор состояния состоит из двух компонент, его можно записать так:

.

Вектор-столбец u[k] – это сигнал управления, поступающий на систему (он тоже может быть векторным). Наконец, y[k] – это сигнал выхода системы. Матрицы A, B, C и D для стационарной системы – постоянные; их размеры таковы, что можно выполнить матричное умножение:

• 
  матрица A имеет размеры , где n – размер вектора x;
  
• 
  матрица B имеет размеры , где m – размер вектора u;
  
• 
  матрица C имеет размеры , где q – размер вектора y;
  
• 
  матрица D имеет размеры .
  

Для системы с двумя состояниями (n = 2), одним входом (m = 1) и одним выходом (q = 1) эти матрицы выглядят так: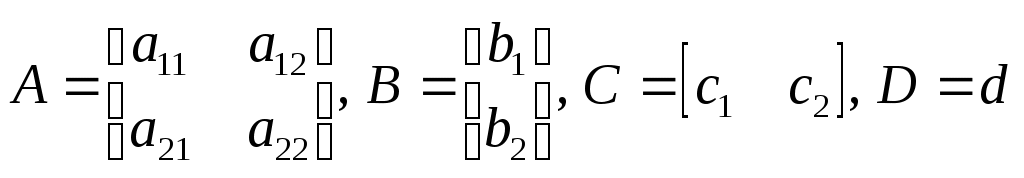

.

где и d – скалярные величины (числа). Тогда матричная запись



может быть переписана в скалярном виде так: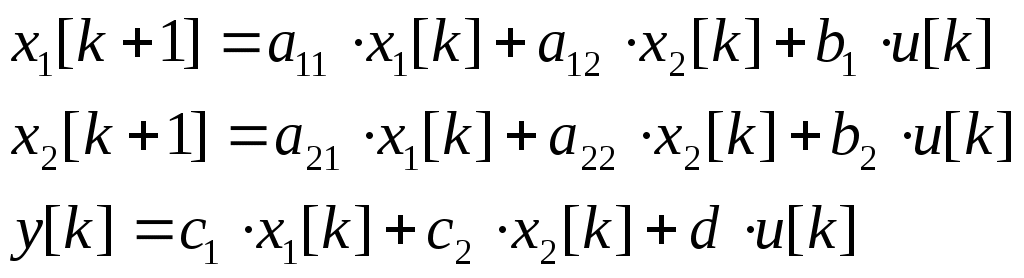



Модель в пространстве состояний в Scilab задаётся c помощью функции syslin:

--> G = syslin('d', A, B, C, D )

Параметр 'd' говорит о том, что система – дискретная (discrete-time).

Передаточная функция системы, заданной моделью в пространстве состояний, может быть получена по формуле

,

где I обозначает единичную матрицу того же размера, что и матрица A. В Scilab такое преобразованиевыполняет функция ss2tf:

--> Gtf = ss2tf ( G )

Функция tf2ss выполняет обратный переход, от передаточной функции к модели в пространстве состояний.

--> G1 = tf2ss ( Gtf )

Выполнив эти команды, вы можете обнаружить, что матрицы модели G₁ отличаются от матриц A, B, C и D, которые мы задали ранее в модели G. Это связано с тем, что одной и той же системе соответствует бесконечное множество моделей в пространстве состояний.

Можно показать, что при любой невырожденной матрице T (определитель которой – не ноль) можно заменить матрицу A на TAT^-1, матрицу B – на TB и матрицу С – на CT^-1 (а матрицу Dоставить без изменений), и мы таким образом построим новую модель в пространстве состояний для той же системы. При этом мы фактически заменяем вектор состояния, переходя от исходного вектора x[k] к новому вектору Tx[k]. Причем этой новой модели будет соответствовать та же самая передаточная функция.

Статический коэффициент усиления системы можно найти по теореме о конечном значении:

.

Можно показать, что при замене A на TAT^-1, B на TB и С на CT^-1 ни передаточная функция, ни статический коэффициент усиления не изменяются.

Устойчивость

Устойчивость модели в пространстве состояний определяется матрицей A. Если система не управляется, то есть u[k] = 0, модель собственного движения системы описывается уравнением



Пусть известны начальные условия: x[0] = x₀. Тогда можно вычислить значения вектора состояния в следующие моменты времени:





…



То, как будет вести себя этот процесс, зависит от собственных чисел  матрицы A, то есть от корней уравнения

,

где det обозначает определитель квадратной матрицы. Матрица размером имеет ровно n собственных чисел (среди них могут быть и пары комплексно-сопряженных чисел). Если все они по модулю меньше 1, система асимптотически устойчива (процесс при любых начальных условиях сходится к нулевому вектору x[k]).

Если некоторые собственные числа матрицы A по модулю равны 1, а остальные – меньше 1, система находится на границе устойчивости. Это значит, что при ненулевых начальных условиях вектор состояния x[k] не стремится к бесконечным значениям, но и не сходится у нулю.

Если у матрицы A есть хотя бы одно собственное число, модуль которого больше 1, система неустойчива – при ненулевых начальных условиях некоторые компоненты вектора состояния стремятся к бесконечности.

Как следует из формулы преобразования , корни уравнения – это как раз корни знаменателя соответствующей передаточной функции . Поэтому для определения устойчивости системы с известной передаточной функции нужно найти её полюса – корни знаменателя. Если все они по модулю меньше 1, система асимптотически устойчива.

Знаменатель передаточной функции называется характеристическим полиномом системы, потому что его корни определяют устойчивость системы.

Моделирование

Для моделирования реакции дискретных моделей в пространстве состояний на заданный входной сигнал используют функцию dsimul. Сначала нужно построить входной сигнал как массив значений. Например, для моделирования на отрезке от 0 до 15 единичный импульсный сигнал строится так:

--> t = [0:15]

--> xImp = zeros(t)

--> xImp(1) = 1

В первой строке программы мы задаем массив значений времени – от 0 до 15. Во второй строке строится сигнал, состоящий из нулей и имеющий тот же размер, что и массив t. Затем в первый элемент этого массива записываем 1 – это (единственное ненулевое) значение сигнала при t = 0.

Теперь остается вызвать функцию dsimul:

--> yImp = dsimul ( G, xImp )

Единичный ступенчатый сигнал строится еще проще – все его значения равны 1, используется функция ones:

--> t = [0:15]

--> xStep = ones(t)

Передаточные функции системы с регулятором

Рассмотрим дискретную систему, в которой дискретный объект с передаточной функцией G(z) управляется регулятором с передаточной функцией C(z):



Если разорвать обратную связь, то получается разомкнутая система: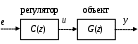



Её передаточная функция равна произведению передаточных функций двух блоков:

W_open(z) = C(z) G(z).

Для замкнутой системы справедлива такая же формула, как и для непрерывных систем:

.

В Scilab эту передаточную функцию можно вычислить так:

W = C*Gtf / (1 + C*Gtf);

Кроме того, в Scilab добавили специальный оператор «/.», и ту же передаточную функцию можно построить иначе:

W = C*Gtf /. 1;

Слева от оператора /. записывается передаточная функция разомкнутой системы (без обратной связи), а справа – передаточная функция отрицательной обратной связи (в данном случае – 1).

Люди, будьте бдительны!

При использовании оператора «/.» с единичной обратной связью после точки обязательно ставить пробел, иначе запись

W = C*Gtf /.1;

воспринимается как

W = C*Gtf / 0.1;

и вычисляет совершенно другую передаточную функцию.