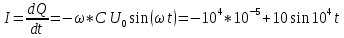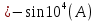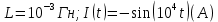Лабораторная_5.1. Лабораторная работа 5. 1 Изучение свободных колебаний в электрическом контуре студент группы мо15 Бригада 2
 Скачать 1.47 Mb. Скачать 1.47 Mb.
|
|
Министерство цифрового развития, связи и массовых коммуникаций Российской Федерации ФГБОУ ВО «СибГУТИ» Кафедра Физики Лабораторная работа №5.1 ИЗУЧЕНИЕ СВОБОДНЫХ КОЛЕБАНИЙ В ЭЛЕКТРИЧЕСКОМ КОНТУРЕ Выполнил: Студент группы МО-15 Бригада №2 Стрельников Евгений Николаевич Проверил преподаватель: Ф.И.О. Преподавателя Измерения сняты: Дата, роспись преподавателя Отчёт принят: Дата, роспись преподавателя Работа зачтена: Оценка, дата, роспись преподавателя Новосибирск, 2021 год. 1. ЦЕЛЬ РАБОТЫ 1. Ознакомиться с физическими процессами, протекающими в электрическом контуре. 2. Исследовать влияние величин электроёмкости и индуктивности на период колебаний в контуре с малым сопротивлением. 3. Установить характер зависимости логарифмического декремента затухания колебаний от сопротивления контура. 2. ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ Исследуемый контур состоит из конденсатора электроёмкостью С, катушки индуктивностью L и резистора, имеющего сопротивление R. Схема соединения элементов электрической цепи приведена на рисунке 1. 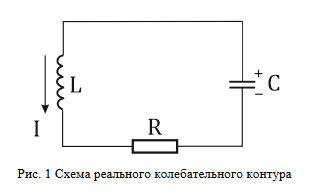 Простой контур, который здесь рассматривается, является электрической цепью со сосредоточенными параметрами. Это означает, что электроемкость С сосредоточена в одном месте (конденсаторе), а индуктивность L и сопротивление R - в других местах контура (в катушке и в резисторе). Электрическими колебаниями в таком случае выступают повторяющиеся изменения электрических величин, характеризующих процессы в элементах контура. В конденсаторе, например, изменяются со временем следующие величины: заряд q и напряжение между обкладками 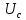 а также характеристики электрического поля конденсатора. Электрические колебания (процессы) происходят во всех элементах цепи согласованно. А именно так, что мгновенные значения силы тока I одни и те же в любом месте контура. Подобное имеет место в цепи постоянного (стационарного) тока. Поэтому электрические процессы в колебательном контуре называются квазистационарными («квази» – приставка, означающая «якобы, как будто»). Квазистационарные процессы также подчиняются закону Ома, что и постоянный ток. а также характеристики электрического поля конденсатора. Электрические колебания (процессы) происходят во всех элементах цепи согласованно. А именно так, что мгновенные значения силы тока I одни и те же в любом месте контура. Подобное имеет место в цепи постоянного (стационарного) тока. Поэтому электрические процессы в колебательном контуре называются квазистационарными («квази» – приставка, означающая «якобы, как будто»). Квазистационарные процессы также подчиняются закону Ома, что и постоянный ток. Для математического описания электрических процессов в контуре применим 2 правило Кирхгофа: «Сумма падений напряжения в контуре равна сумме действующих в нем ЭДС». В колебательном контуре имеются два падения напряжения: на конденсаторе 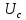 , равное , равное 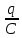 , и на сопротивлении, равное IR. , и на сопротивлении, равное IR. При изменении силы тока в контуре в катушке индуктивности возникает ЭДС самоиндукции. 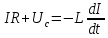 Сила тока по определению связана с зарядом конденсатора соотношением: 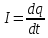 или или 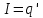 - так обозначается производная по времени. - так обозначается производная по времени. Подставив выражения для тока i и напряжения 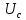 в формулу (1), получим дифференциальное уравнение в виде: в формулу (1), получим дифференциальное уравнение в виде: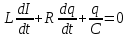 или или 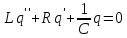 Разделим уравнение на коэффициент при старшей производной (индуктивность катушки) и введем обозначения: 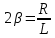 или или 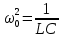 После введения обозначений дифференциальное уравнение затухающих колебаний в контуре принимает вид: 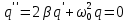 ; ; 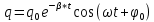 . .Функция является решением дифференциального уравнения (2) и называется уравнением затухающих колебаний заряда конденсатора. Циклическая частота затухающих колебаний: 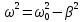 или или 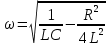 Амплитуда заряда на конденсаторе убывает со временем по экспоненциальному закону: 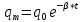 Быстрота убывания определяется величиной β, которую называют коэффициентом затухания. 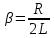 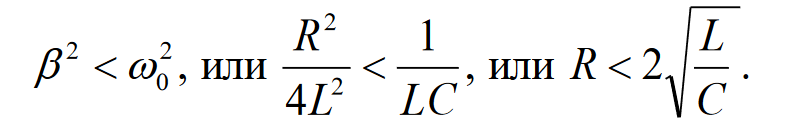 Так как 𝜔 есть действительное число и 𝜔2 не может быть отрицательным, то затухающие колебания имеют место только при условии (см.4): Так как 𝜔 есть действительное число и 𝜔2 не может быть отрицательным, то затухающие колебания имеют место только при условии (см.4):Наконец, постоянные величины  и и  определяются начальными условиями. Если, например, вначале при разомкнутом контуре конденсатор заряжен ( определяются начальными условиями. Если, например, вначале при разомкнутом контуре конденсатор заряжен (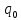 - величины заряда), а потом соединен с катушкой и резистором, то начальная фаза колебаний равна нулю, то есть - величины заряда), а потом соединен с катушкой и резистором, то начальная фаза колебаний равна нулю, то есть 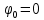 . На рисунке 2 оказаны графики затухающих колебаний в одном электрическом контуре при двух значениях коэффициента затухания. Причем, 𝛽2 > 𝛽1, а величины . На рисунке 2 оказаны графики затухающих колебаний в одном электрическом контуре при двух значениях коэффициента затухания. Причем, 𝛽2 > 𝛽1, а величины 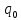 и и 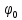 одинаковы. Пунктиром изображена зависимость амплитуды заряда одинаковы. Пунктиром изображена зависимость амплитуды заряда 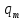 от времени. Эта зависимость называется экспоненциальной. от времени. Эта зависимость называется экспоненциальной.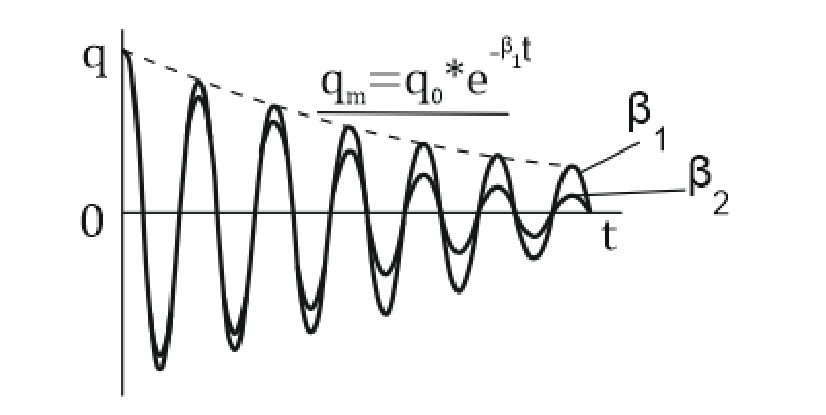 Рисунок 2. Графики затухающих колебаний заряда с разными коэффициентами затухания 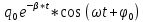 . Так как 𝐼 =𝑞′, то после дифференцирования получим: . Так как 𝐼 =𝑞′, то после дифференцирования получим: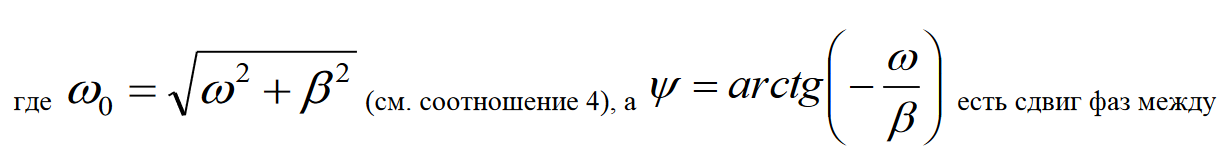 З З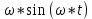 как как 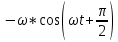 и складывая оба слагаемых выражения в скобках с помощью векторной диаграммы, получим уравнение колебаний тока в виде: и складывая оба слагаемых выражения в скобках с помощью векторной диаграммы, получим уравнение колебаний тока в виде: колебаниями заряда и тока. Полученный результат приводит к следующим заключениям: 1. Амплитуда тока в начальный момент времени 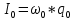 не зависит от характеристик затухания. не зависит от характеристик затухания. 2. В контурах с малым сопротивлением R и достаточно большой частотой 𝜔 реализуется неравенство: 𝛽 ≪𝜔. Это случай слабого затухания, величина сдвига фаз Ψ стремится к ( 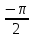 ). Затухание влияет на частоту 𝜔 только во втором порядке. ). Затухание влияет на частоту 𝜔 только во втором порядке. Полученная ранее формула (4) позволяет рассчитать относительную разницу величин 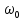 и 𝜔 с помощью соотношения: и 𝜔 с помощью соотношения: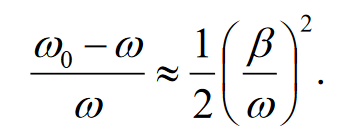 В результате при СЛАБОМ ЗАТУХАНИИ уравнения колебаний заряда и тока можно приближенно записать так: Отметим, что период колебаний 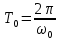 определяется в этом случае известной формулой Томсона: определяется в этом случае известной формулой Томсона: 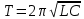 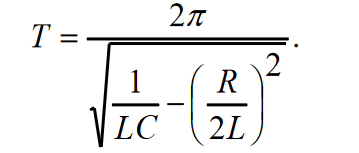 Точное же значение периода затухающих колебаний (в соответствии с формулой (4)) равно: Точное же значение периода затухающих колебаний (в соответствии с формулой (4)) равно: В 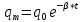 , изображенной на рис. 2, чтобы рассказать о других важных характеристиках затухающих колебаний и дать им физическое объяснение. , изображенной на рис. 2, чтобы рассказать о других важных характеристиках затухающих колебаний и дать им физическое объяснение. Непрерывное рассеяние энергии на сопротивлении приводит к тому, что наибольший заряд конденсатора уменьшается с каждым периодом колебаний, именно: N - число колебаний. Эти амплитуды колебаний образуют убывающую геометрическую прогрессию. А это означает, что отношение величины каждого максимума 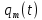 к последующему к последующему 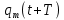 одинаково. одинаково. Безразмерная величина, равная натуральному логарифму отношения амплитудных значений, отстоящих по времени на период колебания, называется логарифмическим декрементом затухания: 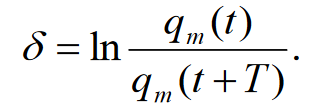 С 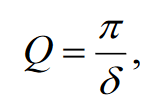 логарифмическим декрементом затухания связана (обратно пропорциональной зависимостью) еще одна характеристика затухающих колебаний - добротность Q. (Не путать с зарядом q!). В случае слабого затухания добротность определяется следующим образом: логарифмическим декрементом затухания связана (обратно пропорциональной зависимостью) еще одна характеристика затухающих колебаний - добротность Q. (Не путать с зарядом q!). В случае слабого затухания добротность определяется следующим образом:то есть, чем меньше затухание, тем больше добротность. Для того, чтобы выявить смысл характеристик затухания, введем понятие времени релаксации 𝜏. Это такой промежуток времени, в течение которого амплитуда колебаний уменьшается в  раз (е2,72- основание натуральных логарифмов). раз (е2,72- основание натуральных логарифмов).Заменив t на в выражении 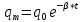 , получим , получим 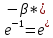 , откуда: , откуда: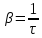 Т 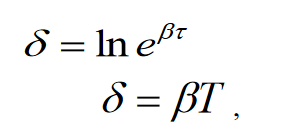 о есть коэффициент затухания 𝛽 - это величина, обратная времени релаксации 𝜏. о есть коэффициент затухания 𝛽 - это величина, обратная времени релаксации 𝜏. Связь коэффициента затухания и логарифмического декремента получают из формулы определения последнего (10): Где T – период колебаний. В 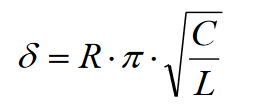 случае слабого затухания можно выразить логарифмический декремент затухания через параметры контура: случае слабого затухания можно выразить логарифмический декремент затухания через параметры контура: 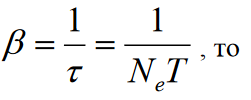 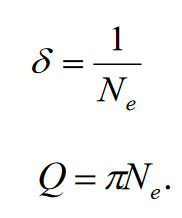 В качестве меры затухания можно использовать также число В качестве меры затухания можно использовать также число 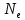 – число колебаний, совершающихся в контуре за время, равное времени релаксации 𝜏. При малом затухании время 𝜏 больше периода колебаний. – число колебаний, совершающихся в контуре за время, равное времени релаксации 𝜏. При малом затухании время 𝜏 больше периода колебаний. Поэтому имеем: так как Т 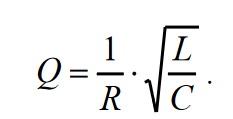 аким образом, логарифмический декремент затухания есть величина, обратная числу колебаний, по истечении которых амплитуда уменьшается в 𝑒 раз. Добротность же прямо пропорциональная числу аким образом, логарифмический декремент затухания есть величина, обратная числу колебаний, по истечении которых амплитуда уменьшается в 𝑒 раз. Добротность же прямо пропорциональная числу  . . Исходя из формул (14) и (16), можно получить формулу зависимости добротности от параметров контура при слабом затухании: Полная картина поведения электрического контура не ограничивается только затухающими колебаниями. В контуре с сильным затуханием (большим сопротивлением R) колебаний заряда нет, есть только монотонное убывание с течением времени. Не будем рассматривать соответствующие решения дифференциального уравнения (2). Заметим только, что специальный случай «критического затухания» имеет место при сопротивлении R, равном в котором величину 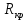 называют критическим сопротивлением контура. называют критическим сопротивлением контура.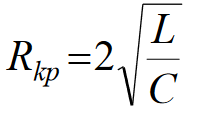 Эта последняя формула подтверждает общую особенность, выражающуюся в том, что все рассмотренные выше характеристики процессов в колебательном контуре имеют связи с численными значениями параметров контура R, L и С. Исследования, проводимые в этой работе, имеют целью проверить некоторые из них. 3. ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ 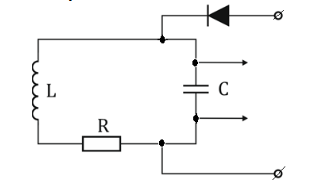 Электрическая цепь собрана по схеме, изображенной на рис. 1. Колебания возбуждаются в контуре благодаря зарядке конденсатора от источника однополупериодного переменного тока с частотой 50 Гц. Электрическая цепь собрана по схеме, изображенной на рис. 1. Колебания возбуждаются в контуре благодаря зарядке конденсатора от источника однополупериодного переменного тока с частотой 50 Гц. Затухающие колебания напряжения 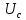 на конденсаторе подаются на клеммы вертикального усиления осциллографа (рис. 3). При этом частоту развертки электрического сигнала осциллографом устанавливают примерно такой же, что и частота зарядки С. на конденсаторе подаются на клеммы вертикального усиления осциллографа (рис. 3). При этом частоту развертки электрического сигнала осциллографом устанавливают примерно такой же, что и частота зарядки С. В качестве элементов колебательного контура используются наборы конденсаторов, катушек индуктивности и сопротивлений (резисторов). Присоединение каждого элемента набора производится с помощью кнопочного выключателя. Для включения элементов R, L, C в цепь контура нужно нажать соответствующие кнопки и зафиксировать их в «утопленном состоянии».  Значения сопротивления R, электроемкости С и индуктивности L для каждого положения кнопочных выключателей составляют отдельную таблицу. Таблица выдается на рабочее место при выполнении работы. Основные измерения проводятся с помощью осциллографа. Осциллограмма напряжения 𝑈𝑐 выглядит так, как показано на рис. 4, то есть подобна графику колебаний заряда на конденсаторе из рис. 2 ( 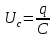 ). ). Время по горизонтальной оси можно рассчитать. Для этого поверх экрана нанесена прямоугольная сетка, калиброванная в единицах времени (мс или мкс). Назовем временную длительность одного квадрата сетки по горизонтали ценой деления развертки и обозначим ее 𝛾. Для более точного измерения каждое деление «разделено» на доли по 0,2 (это указано на сетке). Тогда время t, в течение которого происходят N колебаний, будет равно 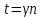 , где n- число квадратов сетки, в пределах которых укладываются эти N колебаний. На рис. 4 видно, что для N=6, то есть для шести периодов Т, число n равно 6,6. Величину 𝛾 отсчитывают непосредственно на панели осциллографа. Отсчёт числа полных колебаний удобно проводить по амплитудным (максимальным) значениям напряжениям. Начало отсчёта «0». На рис. 4 переключатель развертки по горизонтали указывает 0,1. Справа от переключателя нажата кнопка 𝑚𝑠, значит, цена деления равна 0,1 мс. Отсчитываем шесть полных колебаний (N=6). На экране осциллографа время шести колебаний соответствует n=6,7 делениям. Тогда , где n- число квадратов сетки, в пределах которых укладываются эти N колебаний. На рис. 4 видно, что для N=6, то есть для шести периодов Т, число n равно 6,6. Величину 𝛾 отсчитывают непосредственно на панели осциллографа. Отсчёт числа полных колебаний удобно проводить по амплитудным (максимальным) значениям напряжениям. Начало отсчёта «0». На рис. 4 переключатель развертки по горизонтали указывает 0,1. Справа от переключателя нажата кнопка 𝑚𝑠, значит, цена деления равна 0,1 мс. Отсчитываем шесть полных колебаний (N=6). На экране осциллографа время шести колебаний соответствует n=6,7 делениям. Тогда 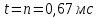 . Время одного колебания, то есть период колебания . Время одного колебания, то есть период колебания 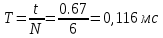 . . Важным параметром затухающих колебаний является время релаксации . За это время амплитуда колебания уменьшается в «е» раз (е=2,72 – основание натурального логарифма). Амплитуду напряжения можно измерять в делениях (одно деление – это сторона квадрата сетки на экране осциллографа по вертикали). Цена деления в данном случае для наших рассмотрений не важна. Важно, чтобы формат изображения был удобен для рассмотрений. На рис. 4 амплитуда напряжения 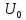 =4 деления. Амплитуда через время релаксации =4 деления. Амплитуда через время релаксации 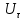 =1,48 деления (42,72 =1,48). Осциллограмма показывает, что уменьшение амплитуды в «е» раз произошло за время =1,48 деления (42,72 =1,48). Осциллограмма показывает, что уменьшение амплитуды в «е» раз произошло за время 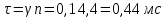 . . С основными органами управления осциллографом следует ознакомиться перед началом измерений. 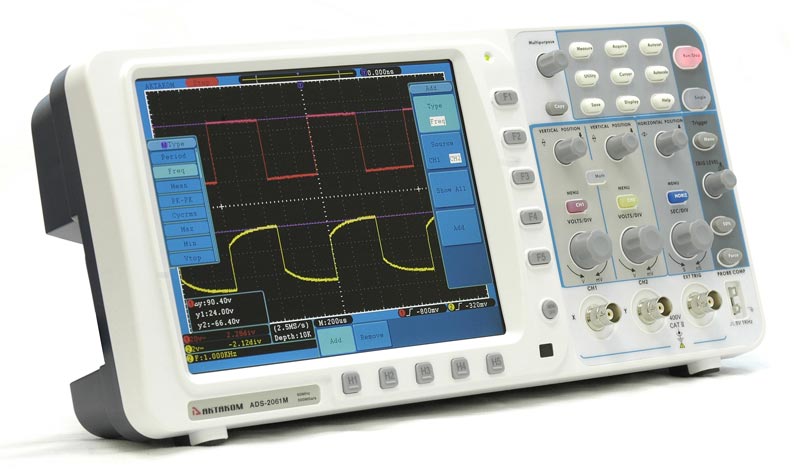 Рис. 6.5 Осциллограф  Рис. 6.6 Экран осциллографа Рассмотрим экран осциллографа поподробнее (рис. 6.6). Цена деления временной развёртки отображается на экране осциллографа, в данном случае γ = 500 μs (500 микросек). Цена деления амплитудной развёртки 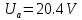 (20.4 В). T – это период колебаний. (20.4 В). T – это период колебаний.  - амплитуда произвольного колебания. - амплитуда произвольного колебания. 4. ВЫПОЛНЕНИЕ РАБОТЫ Задание 1. Определить сопротивление  проводов намотки катушки индуктивности. проводов намотки катушки индуктивности.Дано: 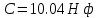 ; ; 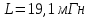 ; ;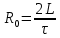 ; ; 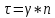 ; ; 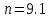 ; ; 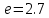 . .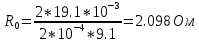 Ответ: Напряжение – 2.098 Ом. Ответ: Напряжение – 2.098 Ом.5. ВЫВОД Ознакомились с физическими процессами, протекающими в электрическом контуре. Исследовали влияние величин электроёмкости и индуктивности на период колебаний в контуре с малым сопротивлением. Установили характер зависимости логарифмического декремента затухания колебаний от сопротивления контура. 6. ОТВЕТЫ НА КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Катушка индуктивности обладает реактивным сопротивлением. Чем больше частота тока, протекающего через катушку – тем больше её сопротивление. Катушка с током запасает энергию в магнитном поле. При замыкании катушки с током на резистор происходит переходной процесс, при котором ток в цепи экспоненциально уменьшается, формула ниже. Уменьшение тока в 2.7 раза передаётся за 3 наносекунды. Частота колебаний в электрическом контуре зависит от ёмкости и индуктивности. 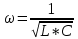 2. Закон Ома, Кирхгофа. Закон сохранения энергии. 3. Отличие – нет сопротивления в формуле. (Идеальный контур не имеет сопротивления) Реальный эл. Контур: 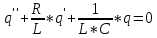 Идеальный: 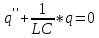 4. Быстрота уменьшения амплитуды напряжения зависит от коэффициента затухания. 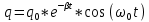 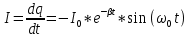 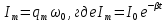 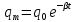 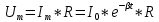 При изменении t, уменьшается 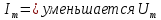 . .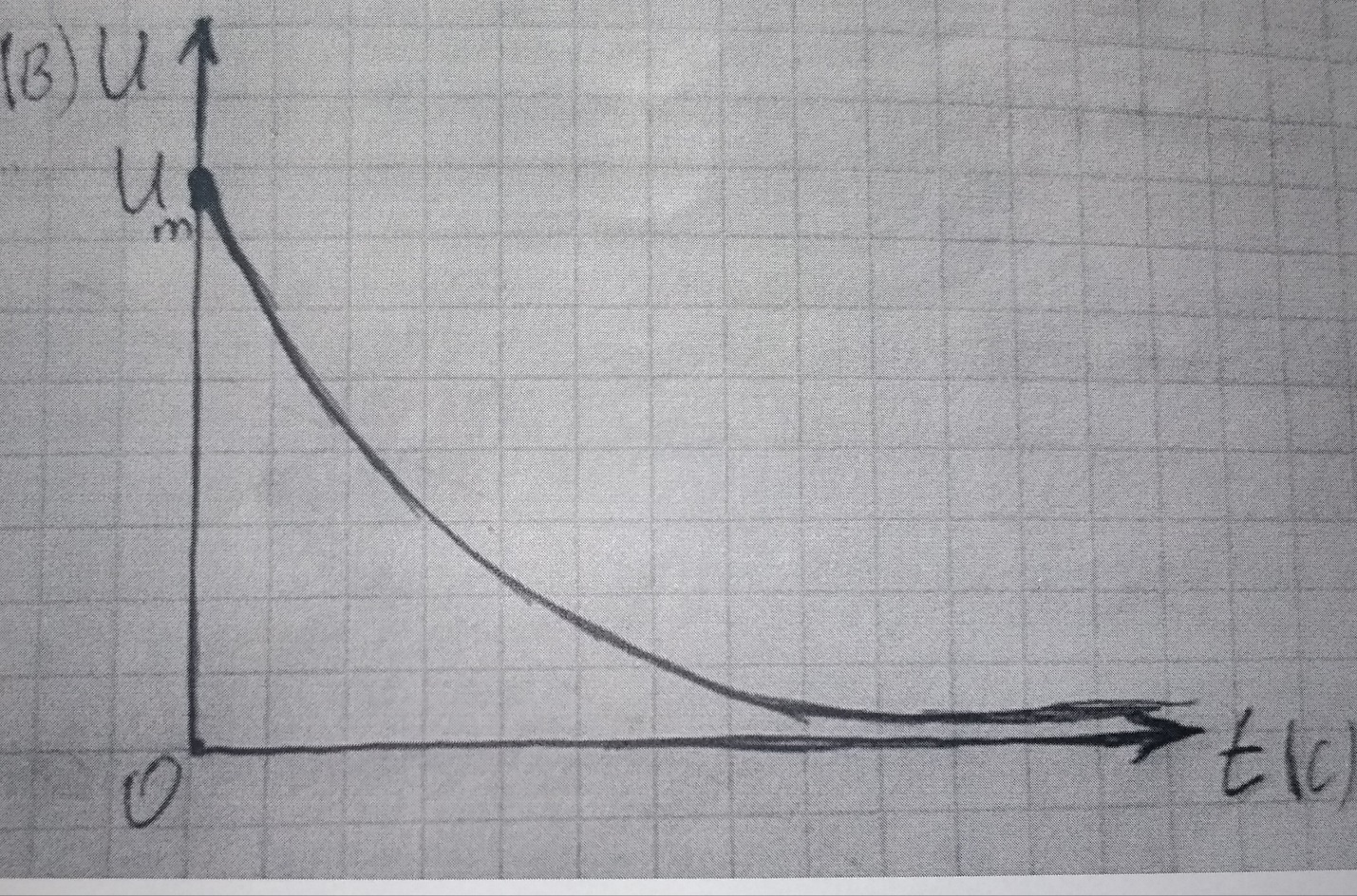 5. Время релаксации – промежуток времени, за который амплитуда колебаний уменьшится в 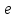 раз (e – основание натурального логарифма) раз (e – основание натурального логарифма)время релаксации зависит от сопротивления: 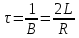 6. Декремент затухания – отношение амплитуд, отличающихся по времени на период. 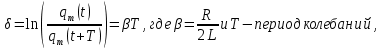 который можно определить как который можно определить как 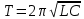 или или 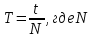 – количество полных колебаний, t – время одного колебания. – количество полных колебаний, t – время одного колебания.Через логарифмический декремент затухания можно выразить добротность 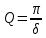 Логарифмический декремент затухания обратно пропорционален числу колебаний, в результате которых амплитуда колебаний уменьшилась в 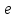 раз. раз.7. Q обратно пропорционален R и C и прямо пропорционален L. Формула работает только при слабом затухании: 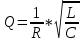 8. a) 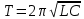 (Формула Томпсона), все формулы согласованны с данными (Формула Томпсона), все формулы согласованны с даннымиб) 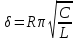 (в случае слабого затухания) (в случае слабого затухания) 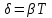 т.к. т.к. 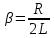 , то получим формулу , то получим формулу 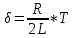 7. ЗАДАЧИ 1.1. Колебательный контур состоит из конденсатора ёмкостью 444 пФ и катушки с индуктивностью 4 мГн. На какую длину волны настроен контур?
1.2. Напряжение на обкладках конденсатора в колебательном контуре меняется по закону 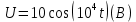 . Ёмкость конденсатора C. Найти индуктивность контура и закон изменения силы тока в нём. . Ёмкость конденсатора C. Найти индуктивность контура и закон изменения силы тока в нём.
|

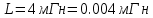
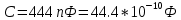
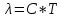
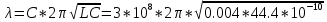
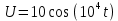
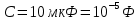
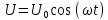 , где
, где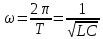 это циклическая частота (в условии задачи
это циклическая частота (в условии задачи 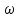 =
= 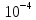 c-1),
c-1), 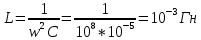
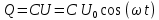 Сила тока по определению
Сила тока по определению