Лабораторная №8. Лабораторная работа 8 Итерационные методы решения алгебраических уравнений

• Название: Лабораторная работа 8 Итерационные методы решения алгебраических уравнений
• Дата: 25.09.2022
• Размер: 353.64 Kb.
• Имя файла: Лабораторная №8.docx
• Тип: Лабораторная работа; #695584

Лабораторная работа №8

Итерационные методы решения алгебраических уравнений

В классификации методов решения линейных алгебраических уравнений (ЛАУ) и систем линейных алгебраических уравнений (СЛАУ) различают точные и итерационные методы. Точные методы позволяют найти решение системы с нулевой погрешностью. Такие решения называются идеальными и находятся при помощи аналитических методов. Обычные «школьные» методы относятся к классу точных. К ним также относятся методы решения СЛАУ «сложения» и «подстановки», более сложные методы Гаусса и Крамера.

Итерационные методы относятся к классу численных методов. Решения ЛАУ и СЛАУ находятся с определенной погрешностью, т.е. точность решения неидеальная. Существует большое количество итерационных методов. В применении к ЛАУ – это методы половинного деления и метод касательных

1. Метод половинного деления (дихотомия).
В методе половинного деления есть одно серьезное ограничение. Данный метод позволяет найти корни уравнения на заданном отрезке только в том случае, если этот корень единственный на заданном отрезке. В связи с этим процесс нахождения корней уравнения методом дихотомии необходимо разбить на два этапа: 1) отделение корней; 2) уточнение корней.

Корнем уравнения f(x) = 0 называется такое значение аргумента x, подстановка которого в уравнение обращает его в тождество. Отделить корень уравнения f(x) = 0 – значит найти такой конечный промежуток (отрезок изоляции), внутри которого имеется единственный корень данного уравнения. Отделение корней можно осуществить аналитически или графически. Но графически намного проще.
Отделение корней.

В качестве примера рассмотрим уравнение: x²+x–100=0 на отрезке [-15, 15], включая концы данного промежутка.

а) Построим график данной функции в каком-либо графическом редакторе, см. рис.1 (Origin, Excel,…).

б) На построенном графике определим координаты по оси ОХ, являющиеся пересечением с графиком функции. Они отмечены красными кружками на рис.1.

в) Очевидно, что на данном отрезке уравнение x²+x-100=0 имеет два корня. Первый корень находится на отрезке (-15, 0), второй – на отрезке (-15, 0).

Итак, корни отделены. Данный этап завершен.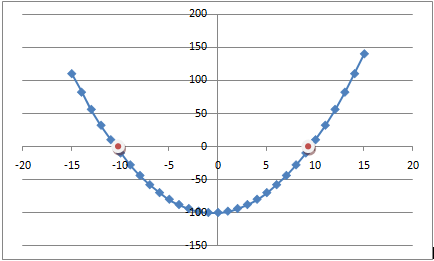



Рис.1. К вопросу об отделении корней.

Уточнение корней.

Поиск приближенного значения корня с точностью до заданного достаточно малого числа ε > 0, называется уточнением этого корня.

Пусть функция f(x) непрерывна на [a, b] и имеет единственный корень на данном отрезке.

Алгоритм поиска корня:

а) Разделим [a; b] пополам точкой c₁ = (a+b)/2 и вычислим значение функции в точке f(c).

б) Если f(c₁) = 0, то корень на данном отрезке является найденным.

Если же f(c₁) ≠ 0, то выполняется следующая последовательность действий. Проводится анализ знакаf(c₁). Если f(c₁) > 0, то проводим корректировку отрезка, на котором проводится поиск решения: [a₁;b₁], где a₁=a, b₁ = c₁ (см. рис.2). Если f(c₁) < 0, то поиск решения будет осуществляться на отрезке: [a₁;b₁], a₁ = c₁, b₁ =b (см. рис.3).

в) Для того, чтобы найти приближенное значение корня с точностью до ε > 0, необходимо остановить процесс половинного деления на таком шаге n, на котором отрезок [a_n; b_n] будет иметь длину b_n - a_n ≤ ε и вычислить x = (a_n + b_n)/2, что и будет являться корнем уравнения.

Если условие b_n - a_n ≤ ε не удовлетворено, что возвращаемся к пункту (а)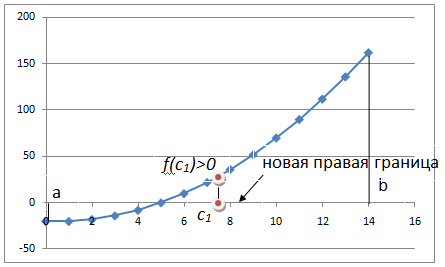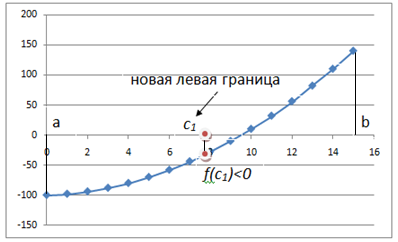



Рис.2. Рис.3

Алгоритм нахождения корней можно описать в виде блок-схемы.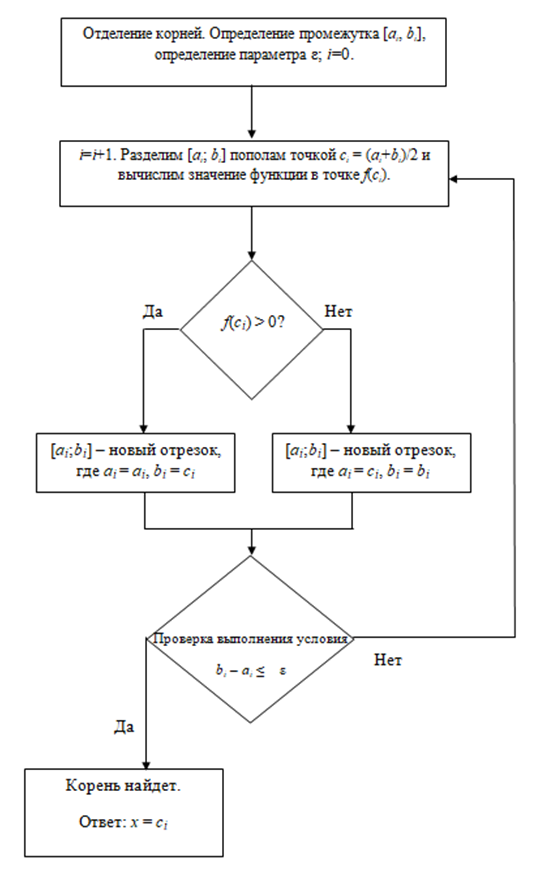



Пример. Найти корни уравнения x²+x – 200=0 на отрезке (-15, 0).

Шаг 1. Отделение корней. Построим график функции на данном промежутке (рис.4). Очевидно, что данное уравнение имеет один корень.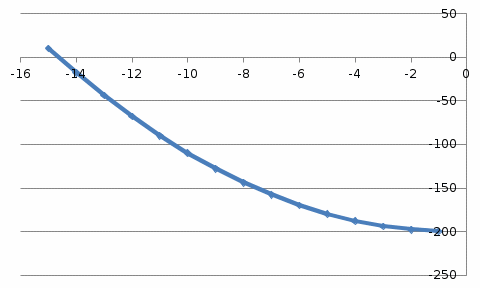



Рис.4.

Шаг 2. Определяем самостоятельно ε = 0.001.

Шаг 3. Построение таблицы. Заполняем ячейки A2 и C2 с использованием условия ЕСЛИ().



Шаг 4. Растягиваем таблицу.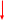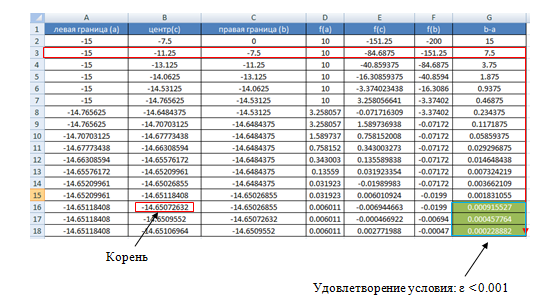





Ответ: x = – 14.6507±0.0009.

2. Метод Ньютона (метод касательных).
Метод касательных называется также методом Ньютона и относится к методам последовательных приближений. Данный метод является методом уточнения корней, т.е. применяется после операции отделения корней.
Условия применения метода касательных:

Пусть дано уравнение f(x) = 0 и на отрезке [a; b] находится единственный корень x, причем значения функции на концах отрезка f(a) и f(b) имеют разные знаки. Кроме того, функция имеет непрерывные производные первого и второго порядков с отличными от нуля и сохраняющими постоянный знак значениями при всех x, принадлежащих отрезку [a; b]. Иными словами, даже если на отрезке [a; b] уравнение имеет один корень, метод касательных неприменим (см. рис.6), поскольку график имеет точку перегиба, в которой производная равна 0.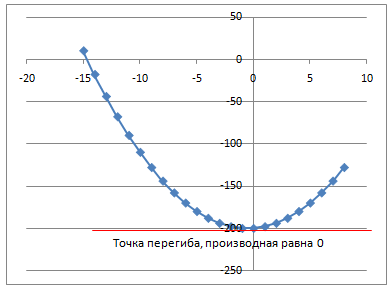


Рис.6. Метод касательных неприменим, поскольку график имеет точку перегиба.

Проведем касательную к кривой y = f(x) в точке A(a; f(a)) до пересечения с осью OX (см. рис. 7). Из курса аналитической геометрии известно, что прямая с известным угловым коэффициентом k и проходящая через данную точку (x0; y0), описывается уравнением:

y-y₀ = k(x-x₀).

В нашем случае это можно записать в виде:

y – f(a) = f ’(a)*(x-a), (*)

где f ’(a) – угловой коэффициент, характеризующий наклон касательной. Полагая, что y=0 в точке x=x1 (см. рис.7), уравнение (*) записывается в виде:

x₁ = a – f(a) / f ‘(a),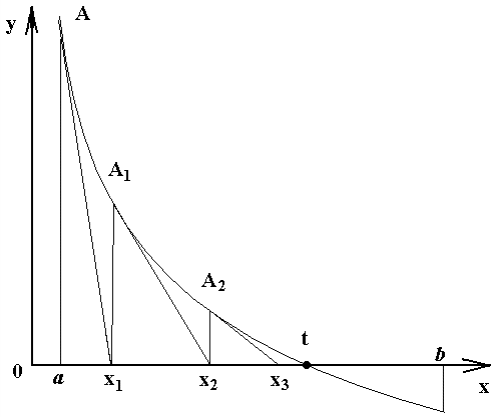



Рис.7

где f‘(a) ≠ 0. Полученное значение x₁ – это первое приближение к корню. Проведя касательную через точку A₁(x₁; f(x₁)) и найдя точку ее пересечения с осью Ox, получим x₂ – второе приближение к корню. Аналогично определяются последующие приближения:

x_n+1 = x_n - f(x_n) / f ‘(x_n).

Это рабочая формула для нахождения корня уравнения методом касательных.

Правило: в качестве начального приближения x₀ в методе касательных удобно выбирать один из концов отрезка [a; b], причем при f ’ (x)*f ‘’(x) >0 следует брать x₀ = b (правый конец), а при f ’ (x)*f ‘’(x) < 0 следует брать x₀ = a(левый конец).

Пример. Методом касательных найти корень уравнения x³ + x – 3 = 0 с точностью до 5-го знака после запятой.

Шаг 1. Отделение корней. Построим график зависимости (рис.8). Корень находится в диапазоне [–10; 10].

Шаг 2. Найдем производные: f ‘(x)= 3x² + 1 и f ’’(x) = 6x. Вычислим значения производных на концах отрезка: f ‘(-10)= 300, f ‘’ (-10)= -60, f ‘(10)= 301, f ‘’ (10)= 60. Т.к. на обоих концах отрезка производные разных знаков, то в качестве нулевого приближения выбираем x₀ = a, т.е. x₀ = –10 .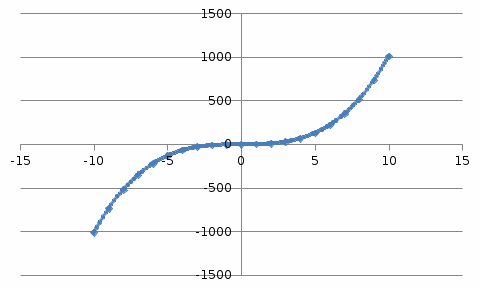



Рис.8.

Шаг 3. Результаты вычислений по формуле (*) записываем в виде таблицы. Ищем значение x, при котором f(x) < ε.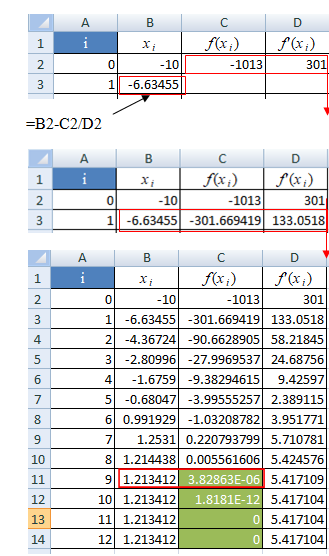



При ε < 0.00001, корень x = 1.213±3.28*10^-6.

Задачи для самостоятельного решения

Найти все корни уравнений на заданных промежутках методами (1) половинного деления и (2) методом касательных. Для каждого уравнения провести исследование точности нахождения корней для трех различных значений ε. Для уравнения 1 провести сравнение численного и аналитических решений и самим определить отрезок для нахождения корней.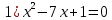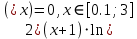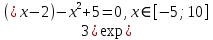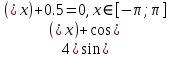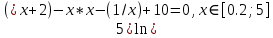











Особое внимание уделить корректности нахождения отрезка для метода касательных.