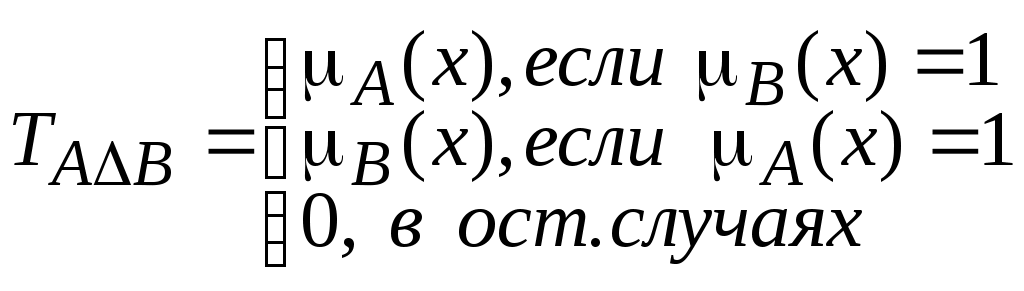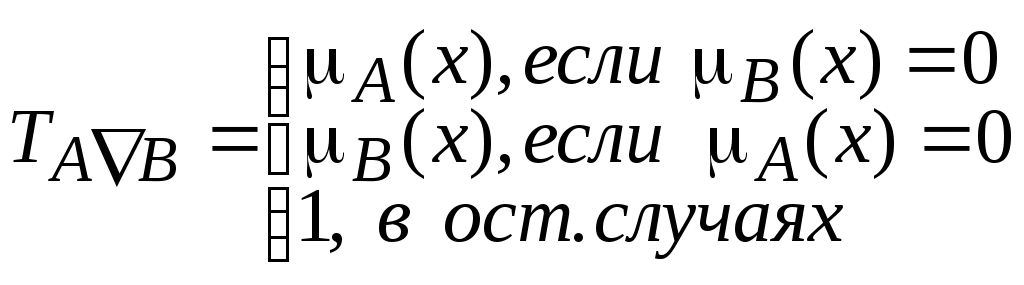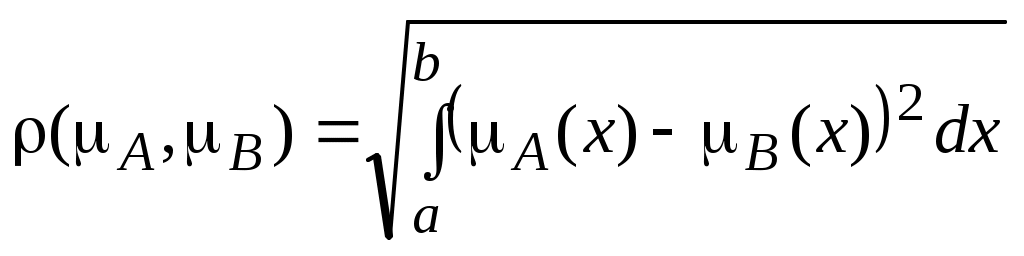Технические охраны. Лабораторная работа 1. Лабораторная работа Нечеткие множества и операции над ними

• Название: Лабораторная работа Нечеткие множества и операции над ними
• Анкор: Технические охраны
• Дата: 06.03.2023
• Размер: 2.24 Mb.
• Имя файла: Лабораторная работа 1.doc
• Тип: Лабораторная работа; #972490

Лабораторная работа 1. Нечеткие множества и операции над ними

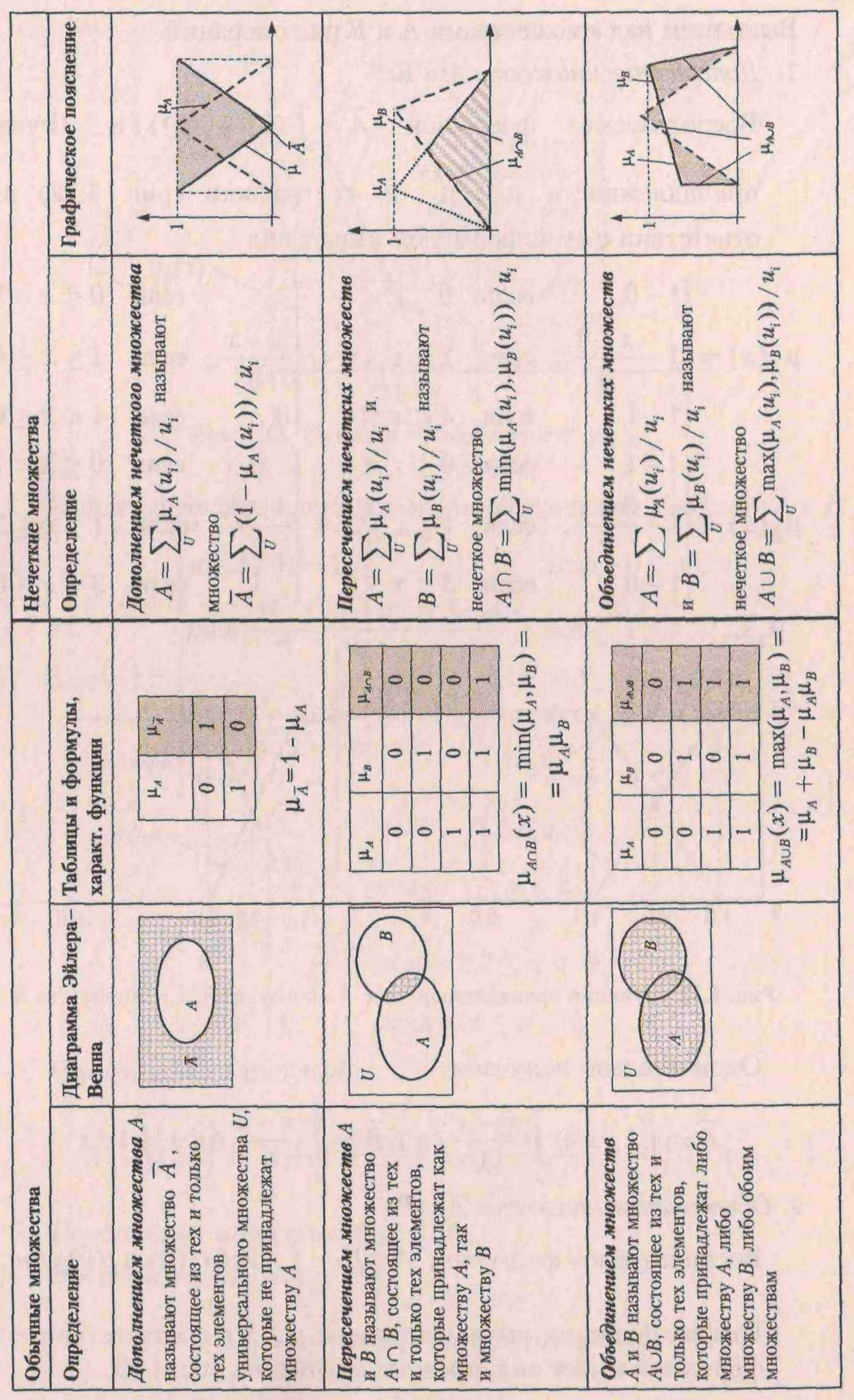
Лабораторная работа 1.

Нечеткие множества и операции над ними

Цель работы: изучить основные операции над нечеткими множествами.
Операции над обычными (четкими) множествами были изучены в курсе дискретной математики. Напомним определение алгебраической операции, заданной на каком-либо множестве X(например, на множестве действительных чисел).

Двуместной, или бинарной, алгебраической операцией на множестве X называют соответствие, по которому каждой паре (а,b) элементов множества X сопоставляется определенный элемент с множества X.

Например, бинарными алгебраическими операциями на множестве действительных чисел R являются сложение и умножение: для любых двух действительных чисел (а,b) найдется единственное число с, которое является их суммой, и единственное число d, которое является их произведением:



Одноместной, или унарной, алгебраической операцией на множестве Xназывают соответствие, по которому каждому элементу а множества Xсопоставляется определенный элемент bмножества X. Например, унарной алгебраической операцией на множестве действительных чисел К является нахождение противоположного числа: для любого числа а найдется единственное противоположное число −а.

В первую очередь рассмотрим три основные алгебраические операции на множестве всех нечетких подмножеств множества U:

1. 
   дополнение ;
   
2. 
   пересечение ;
   
3. 
   объединение .
   

Определения этих операций над обычными и нечеткими множествами, а также геометрические иллюстрации к определениям даны в табл. 1.

Таблица 1.. Операции над обычными и нечеткими множествами

Определения операций над нечеткими множествами записаны для случая дискретного универсального множества. Если же Uнепрерывно, то результаты выполнения этих операций должны быть записаны следующим образом:

1. 
   дополнение
   
2. 
   пересечение
   
3. 
   объединение
   

Рассмотрим пример выполнения этих операций.

Пример 1.

Пусть U={1, 2, ... 10}, А = 0,8/3 + 1/5 + 0.6/6, В = 0.7/3 + 0.5/6.

= (1 - 0)/1 + (1 - 0)/2 + (1 – 0.8)/3 + (1- 0)/4 + (1 - 1)/5 + (1 – 0.6)/7 + (1 - 0)/8 + (1 - 0)/9 + (1 - 0)/10 = 1/1 + 1/2 + 0.2/3 + 1/4 + 0/5 + 0.4/6 + 1/7 + 1/8 + 1/9 + 1/10.

Обратим внимание на то, что в записи нечеткого множества А участвуют лишь элементы несущего множества {3, 5, 6}, т. е. подмножества U, на котором значения функции принадлежности . На подмножестве {1, 2, 4, 7, 8, 9, 10} . Следовательно, согласно формулам (см. табл. 1), на этих элементах

Учитывая это замечание, запишем

=1/1+1/2+ 0.3/3 + 1/5 + 0.5/6+1/7+1/8+1/9+1/10.

В соответствии с формулами (см. табл. 1), выполним другие операции над множествами А и В:





Ø;

=1/1 + 1/2 + 0.7/3 + 1/4 + 1/5 + 0.5/6 + 1/7 + 1/8 + 1/9 + 1/10 ≠ U.

Пересечение нечеткого множества со своим дополнением может не быть пустым ( Ø), а объединение ‑ не составлять универсальное множество ( ).

В теории нечетких множеств помимо логических операций объединения и пересечения используются дополнительные (альтернативные) операции, позволяющие учесть разнообразные смысловые оттенки соответствующих им связок «И», «ИЛИ»: алгебраические (вероятностные), ограниченные, драстические.

Большой класс подобных операций допускает обобщенное представление на основе так называемых нечетких операторов. Эти операторы действуют на множествах значений функций принадлежности (на интервале [0,1]) и поэтому могут быть непосредственно применены к функциям принадлежности произвольных нечетких множеств. Из многообразия нечетких операторов наибольший интерес представляют треугольные норма и конорма (T-норма, Т-конорма или S-норма).

ПАРЫ НОРМ и КОНОРМ

T-норма Т(A, B)	Т-конорма S(A, B)
Логическое произведение Tmin(A, B)= min{A, B}	Логическая сумма Smax(A, B)=max{A, B}
Алгебраическое произведение Tprod(A, B)= A*B	Алгебраическая сумма Ssum(A, B)=A+B−A*B
Граничное произведение Tmax(A, B)=max(0, A+B−1)	Граничная сумма Smin(A, B)=min(1, A+B)
Драстическое произведение	Драстическая сумма

На основе операции алгебраического произведения определяется операция возведения в степень  нечеткого множества А (>0). НМ А^ определяется следующей ФП:

.

Частными случаями возведения в степень являются:

а) операция концентрации (concentration):

CON(A)=А²; .

б) операция растяжения (dilation):

DIL(A)=А^0,5; .

Меры нечеткости множества

Пусть U − универсальное множество. Очевидно, что «самое четкое» его подмножество − это обычное множество, функция принадлежности (характеристическая функция) которого принимает значение 0 или 1. «Самое нечеткое» подмножество − это множество, состоящее из точек перехода, в которых функция принадлежности принимает значение 0.5:

Пусть А − какое-либо нечеткое подмножество множества U. Если близко к значению 1 или 0, то вклад элемента u₀в нечеткость множества А мал. Если же близко к значению 0.5 или, что то же самое, значительно отличается как от 1, так и от 0, то его вклад в нечеткость А будет значителен. Таким образом, вклад в нечеткость каждого элемента множества определяется близостью значения функции принадлежности на этом элементе к числам 1 и 0 или отдаленностью от них. Естественно определить меру нечеткости всего множества как сумму вкладов каждого его элемента.

Исходя из этих соображений мерой нечеткости множества А является функция, которая множеству А ставит в соответствие определенное действительное число d(А), удовлетворяющее следующим требованиям:

1. 
   d(A) = 0 тогда и только тогда, когда А − обычное множество;
   
2. 
   d(А)принимает максимальное значение тогда и только тогда, когда µ(и) = 0.5;
   
3. 
   если при любом 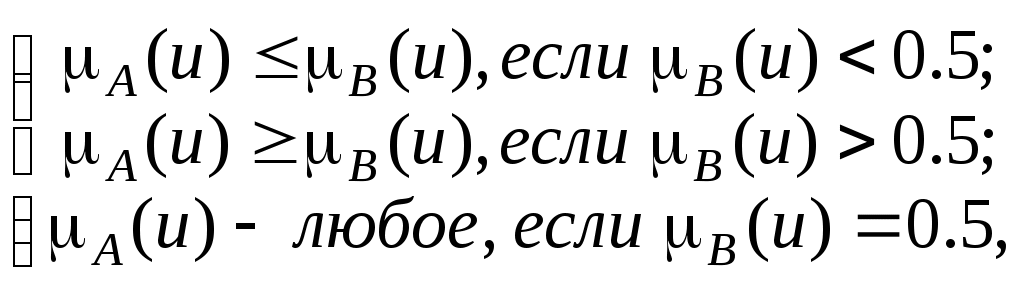функции принадлежности множеств А и В связаны соотношениями:
   

то d(А) ≤ d(B);

4. 
   если , то d(А)=d(B). (Симметричность относительно точки перехода, в которой функции принадлежности принимают значение 0.5.)
   

Требования 1−4 называют аксиомами меры нечеткости. Чаще всего в качестве меры нечеткости выбирают расстояние от нечеткого множества А до ближайшего к нему обычного множества А₀.

Дадим определение понятия «обычное множество, ближайшее к нечеткому».

Определение 1. Обычным множеством, ближайшим к не­четкому множеству А с функцией принадлежности 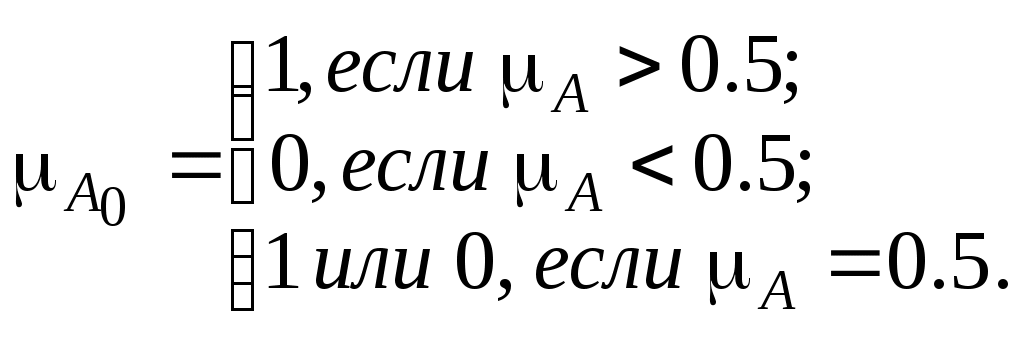, называют подмножество A₀ множества U, характеристическая функция которого имеет вид:

(1)

Геометрический смысл понятия «обычное множество А₀, ближайшее к нечеткому множеству А» иллюстрирует рис. 1.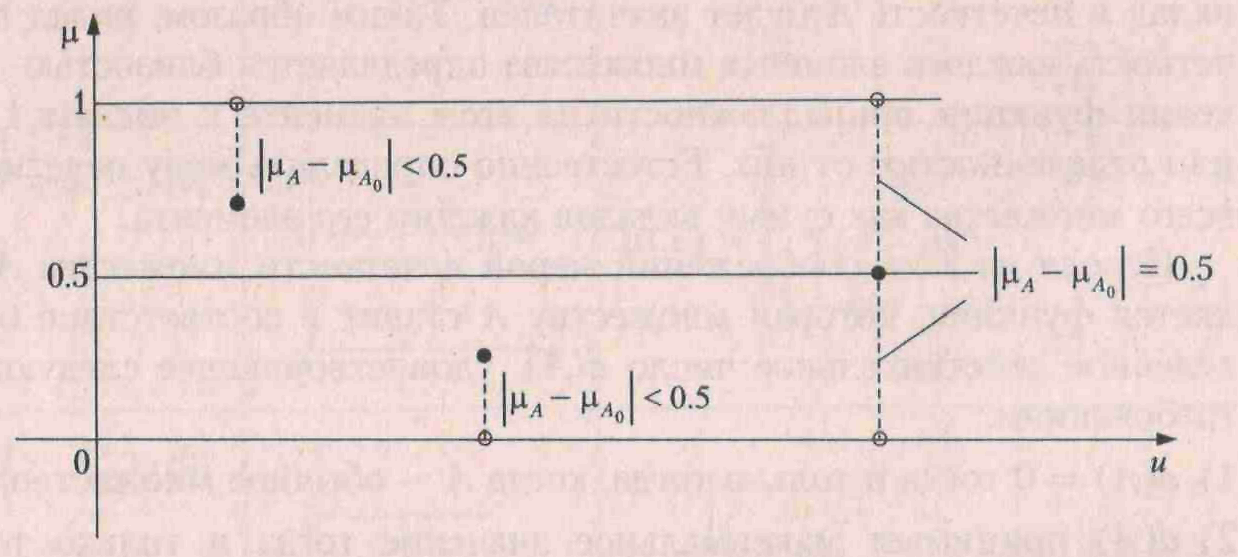



Рис. 1. Значения | | при различном расположении точек графиков функций: • − функция ; ° − функция

Как видно из рисунка, справедливы неравенства

| |<0.5, если >0.5 или <0.5;

| |=0.5, если =0.5, независимо от того = 1 или = 0.

Если А − обычное множество, то оно является ближайшим к самому себе. Это следует непосредственно из определения 1.

Необходимо договориться о том, каким образом определять расстояние между множествами (четкими и нечеткими). Функции принадлежности всех множеств на универсальном множестве Uобразуют функциональное множество М. Другими словами, М − это множество всех функций, определенных на Uи принимающих значения на отрезке [0,1]. Определить расстояние между элементами множества М означает наложить метрику на это множество. Метрика на каком-либо множестве X − это функция ρ(х,у), сопоставляющая каждой паре элементов действительное число и обладающая следующими свойствами (аксиомы метрики):

1. 
   аксиома тождества ρ(х, у) ≥ 0,
   

причем ρ(х, у) =0 тогда и только тогда, когда х = у;

2. 
   аксиома симметрии ρ (х, у) = ρ(у, х);
   
3. 
   аксиома треугольника ρ(х, у) ≥ ρ(х, z) + ρ(z, у).
   

Значение ρ(х,у) называют расстоянием между элементами х и у ( ). Напомним, что при изучении векторной алгебры рассматривались множества точек плоскости или пространства и для определения расстояний между точками А(х₁, у₁, z₁) и В(х₂, у₁, z₂) использовалась так называемая евклидова метрика:



Строго говоря, правило вычисления расстояний между элементами множества может быть задано любой формулой, лишь бы полученный результат удовлетворял аксиомам метрики. В функциональных пространствах наиболее часто используют два способа вычисления расстояний (табл. 2).

Таблица 2. Некоторые виды метрик функциональных пространств¹

Вид метрики	Вид множества
	U – дискретное множество, n – число его элементов	U = [a,b]– непрерывное множество
Расстоя-ние Хемминга(линей-ное)
Евклидово расстоя-ние

Мера нечеткости множества, определенная как расстояние от этого множества до ближайшего к нему обычного множества



удовлетворяет аксиомам метрики независимо от того, какая их них (линейная или евклидова) при этом использована.

Рассмотрим пример.

Пример 2. Пусть даны нечеткие множества

А = 0.3/1 + 0.5/2 + 0.2/3 + 0.7/4 + 0.6/5;

В = 0.7/1 + 0.5/2 + 0.8/3 + 0.3/4 + 0.4/5;

С = 0.5/1 + 0.5/2 + 0.5/3.

Обратим внимание на то, что множества А и В удовлетворяют условию четвертой аксиомы меры нечеткости, т. е. их функции принадлежности симметричны относительно точки перехода 0.5:



Согласно второй аксиоме меры нечеткости, самым нечетким множеством должно быть множество С, так как все значения равны 0.5. Найдем меры нечеткости множеств А, В и С, использовав разные метрики. Для этого выполним последовательно следующие действия:

1) найдем обычные множества, ближайшие к А, В и С:

А₀ = 0/1 + 0/2 + 0/3 + 1/4 + 1/5;

В₀ = 1/1 + 0/2 + 1/2 + 0/4 + 0/5;

С₀ = 0/1 + 0/2 + 0/3;

2) вычислим меру нечеткости по линейной метрике:

d^L(A) = |0.3-0| + |0.5-0| + |0.2-0| + |0.7-1| + |0.6 – 1| = 1.7,

d^L(B) = |0.7-1| + |0.5-0| + |0.8-1| + |0.3-0| + | 0.4-0| = 1.7,

d^L(C) = |0.5-0| + |0.5-0| + |0.5-0| = 1.5;

3) вычислим меру нечеткости по метрике Евклида:







Очевидно, что независимо от выбора метрики d(А)=d(В),т. е. принятая мера удовлетворяет четвертой аксиоме меры нечеткости. Но мера нечеткости множества С оказалась при обеих метриках ниже, чем множеств А и В, что на первый взгляд противоречит второй аксиоме. Однако противоречие это только кажущееся, так как носитель множества С не равен носителю множеств А и В: U_с={1, 2, 3}, U_A = U_B= {1, 2, 3, 4, 5}. Выйти из этого положения можно двумя способами: во-первых, можно дополнить носитель множества С элементами 4 и 5, на которых функция должна иметь «вполне четкие» значения ‑ 0. Это объяснит, почему множества А и В являются более нечеткими, чем С; во-вторых, модифицировать выбранную меру нечеткости так, чтобы с ее помощью можно было сравнивать нечеткость множеств на различных носителях.

Примечание. A₀ − обычное множество, ближайшее к нечеткому множеству А, − характеристическая функция множества А₀, вычисляемая по формуле (1). Чтобы с помощью можно было сравнивать нечеткие множества, имеющие различные носители, надо нормировать , потребовав, чтобы для любого множества мера нечеткости не превышала какой-то определенный порог, например 1. Нормированное расстояние между нечетким множеством А и ближайшим к нему обычным множеством называют индексом нечеткости и обозначают I_A (табл. 3).

Таблица 3. Основные формулы вычисления индексов нечеткости множеств

Вид метрики	Вид множества
	U – дискретное множество, n – число элементов носителя	U = [a,b]– непрерывное множество
Индекс нечеткос-ти по Хеммингу(линей-ный)
Индекс нечеткос-ти по Евклиду

Применим формулы, приведенные в табл. 3, для вычисления индексов нечеткости множеств А, В и С, рассмотренных выше. Учитывая формулы из табл. 2 и выполненные ранее вычисления расстояний между этими множествами, получим:

, ,

, .

Как и следовало ожидать, самое нечеткое множество − множество С − имеет самые большие индексы нечеткости. Таким образом, чтобы ответить на вопрос «Какое из двух множеств «более нечетко?», надо вычислить и сравнить индексы нечеткости этих множеств. «Более нечетким» является то множество, которое имеет больший индекс нечеткости.

Задание на лабораторную работу 1
Дано множество X={x₁, x₂, … x_n}и два его нечетких подмножества: A = {x_i, µ_A(x_i)} и B = {x_i, µ_B(x_i)}, x_iX, i=1,2,…,n.
Выполнить следующие действия.

1. 
   Определить характеристики нечетких множеств: носитель, точка перехода, α-срез, ядро, высота, ближайшее четкое множество.
   
2. 
   Вычислить индекс нечеткости по Хэммингу и Евклиду. Определить, какое из нечетких множеств А или В является более нечетким. Вычисления выполнить в MSExcel.
   
3. 
   Построить графики функций принадлежностей нечетких множеств А и В в MSExcel.
   
4. 
   Построить графики функций принадлежностей для дополнения, объединения и пересечения (логическое, алгебраическое, граничное, драстическое), возведения в степень нечетких множеств А и В в MSExcel.
   
5. 
   Сделать выводы.
   

Контрольные вопросы.

1. 
   Дайте определение понятия «нечеткое множество».
   
2. 
   Дайте определение понятия функции принадлежности.
   
3. 
   Назовите основные характеристики нечетких множеств.
   
4. 
   Дайте понятие меры нечеткости. Как определяются индексы нечеткости?
   
5. 
   Назовите основные виды операций над нечеткими множествами.
   
6. 
   Какие существуют дополнительные виды операций объединения и пересечения?
   
7. 
   Что такое нечеткие операторы? Приведите примеры Т-нормы и S-нормы.
   

Таблица 4. Варианты заданий

Вариант 1
	x1	x2	x3	x4	x5	x6	x7	x8
µA(xi)	0,2	0,8	0,5	1	0	0,9	0,3	0,4
µB(xi)	0,7	0	0	0,6	0,4	1	0	0,4
Вариант 2
	x1	x2	x3	x4	x5	x6	x7	x8
µA(xi)	1	0,6	0,3	0	0	0,5	0,5	0,9
µB(xi)	0,7	0,4	0	0,5	0,8	1	1	0,6
Вариант 3
	x1	x2	x3	x4	x5	x6	x7	x8
µA(xi)	0,5	0,3	0	0,8	0,9	1	0,4	0,2
µB(xi)	0,5	1	1	0,8	0,4	0	0	0,5
Вариант 4
	x1	x2	x3	x4	x5	x6	x7	x8
µA(xi)	0	0	0,7	0,6	0,1	0,5	0,8	1
µB(xi)	0,5	0,3	0	0,6	0,7	1	0,7	0,5
Вариант 5
	x1	x2	x3	x4	x5	x6	x7	x8
µA(xi)	0,4	0,7	0,2	0	0,3	0,7	1	0,7
µB(xi)	0,5	0,1	0	0,5	0,7	0,9	1	1
Вариант 6
	x1	x2	x3	x4	x5	x6	x7	x8
µA(xi)	1	1	0,6	0	0,7	0,4	0,1	0
µB(xi)	0,6	0,9	0,5	0,3	0	0,5	1	0,7
Вариант 7
	x1	x2	x3	x4	x5	x6	x7	x8
µA(xi)	0,5	0,8	1	0,4	0	0	0,2	0,6
µB(xi)	0,5	0,2	0,1	0	0	0,6	0,8	0,6
Вариант 8
	x1	x2	x3	x4	x5	x6	x7	x8
µA(xi)	0,6	0,4	0,8	0,5	0,9	0,3	0	0,2
µB(xi)	0,8	0,6	0,9	1	1	0,3	0	0
Вариант 9
	x1	x2	x3	x4	x5	x6	x7	x8
µA(xi)	1	0,5	0,6	0,9	0	0,5	0,4	0,2
µB(xi)	0	0,7	0,8	0,9	0,5	1	1	0
Вариант 10
	x1	x2	x3	x4	x5	x6	x7	x8
µA(xi)	0,4	0,5	0,2	0	0,5	0,7	0,9	1
µB(xi)	0,4	0,2	0,6	0,9	1	0,7	0,3	0,1

1 В табл. 2 знаки суммы и интеграла означают именно сложение и интегрирование, но не объединение множеств.