Предмет методы оптимизации, лабораторные работы. Лабораторные работы, Методы оптимизации. Лабораторная работа одномерная оптимизация Л. И. Лыткина подпись, дата инициалы, фамилия
 Скачать 243.66 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «Сибирский государственный университет науки и технологий имени академика М. Ф. Решетнева» Институт информатики и телекоммуникаций (институт) Кафедра информатики и вычислительной техники (кафедра) ЛАБОРАТОРНАЯ РАБОТА Одномерная оптимизация Руководитель: ____________ Л.И. Лыткина подпись, дата инициалы, фамилия Обучающийся: БИСЗ19-01, 191214007 ____________ С.А. Горбунова номер группы, зачетной книжки подпись, дата инициалы, фамилия Красноярск 2022 Лабораторная работа 1: Метод дихотомии. Задание: Минимизировать функцию  на отрезке  с заданной точностью  = 0,5, принять  =0,2. Использовать три знака после запятой.Для расчетов нам понадобится следующая теория о методе:     Рисунок 1. Теория метода дихотомии Решение: Вычислим середину интервала c1=(0+8)/2=4,0 и точки 1 с1 = 4,0-0,2=3,8 ; 1 с1 = 4+0,2= 4,2. Дальнейшие расчеты представлены в таблице на рисунке 2.  Рисунок 2. Таблица расчетов. Так как на 8-ой итерации |bk-ak|<  , то вычисляем точку минимума функцииxmin=(ak+bk)/2=1,358; f(xmin)=24,315 Ответ: f(xmin)=24,315 Лабораторная работа 2: Метод золотого сечения. Задание: Минимизировать функцию на отрезке с заданной точностью = 0,5. Использовать три знака после запятой.Найдем минимум функции: f(x) = 4.4•x2+22/x Используем для этого Метод золотого сечения. Решение. Положим a1 = a, b1 = b. Вычислим λ1 = a1 + (1- 0.618)(b1 - a1)=3.056, μ1 = a1 + 0.618(b1 - a1) = 4.944. Вычислим f(λ1) = 48.2912, f(μ1) = 111.9996 Итерация №1. Поскольку f(λ1) < f(μ1), то b2 = 4.944, a2 = a1, μ2 = 3.056, f(μ2)=111.9996 λ2 = a2 + (1-0.618)(b2 - a2) = 0 + (1-0.618)(4.944 - 0) = 3.056, f(3.056) = 48.2912 Итерация №2. Поскольку f(λ2) < f(μ2), то b3 = 3.056, a3 = a2, μ3 = 1.8886, f(μ3)=48.2912 λ3 = a3 + (1-0.618)(b3 - a3) = 0 + (1-0.618)(3.056 - 0) = 1.8886, f(1.8886) = 27.3429 Итерация №3. Поскольку f(λ3) < f(μ3), то b4 = 1.8886, a4 = a3, μ4 = 1.1674, f(μ4)=27.3429 λ4 = a4 + (1-0.618)(b4 - a4) = 0 + (1-0.618)(1.8886 - 0) = 1.1674, f(1.1674) = 24.8418 Итерация №4. Поскольку f(λ4) > f(μ4), то a5 = 0.7214, b5 = b4, λ5 = 1.1674, f(λ5)=32.7844 μ5 = a5 + 0.618(b5 - a5) = 0.7214 + 0.618(1.8886 - 0.7214) = 1.4428, f(1.4428) = 24.8418 Остальные расчеты сведем в таблицу.
|24.6707-24.3288|≤0.5 Находим x как середину интервала [a,b]: x=(1.6131+1.1674)/2=1.390247744 Ответ: x = 1.390247744; F(x) = 24.3288 Лабораторная работа 3: Метод Фибоначчи. Задание: Минимизировать функцию  на отрезке 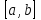 . Известно, что можно выполнить n=6 вычислений функции, =0,01. Значение не использовать.Найдем минимум функции: f(x) = 4.4•x2+22/x Используем для этого Метод Фибоначчи. Важнейшая особенность этого метода состоит в том, что он позволяет для заранее заданного числа вычислений функции построить оптимальную процедуру поиска минимума унимодальной функции. Предположим, что заданный начальный интервал неопределенности [a1,b1], [ai,bi] является интервалом неопределенности, полученным на i-той итерации. Рассмотрим две точки λi и μi из интервала [ai,bi], заданные с помощью соотношений:   где n - заданное число вычислений функции; Fk - последовательность чисел Фибоначчи, заданная с помощью рекуррентной формулы: Fk+1 = Fk + Fk-1, k = 1,2, … , где F0 = F1 = 1 Новый интервал неопределенности (ai+1,bi+1) равен (λi,bi), если f(λi) > f(μi), и равен (ai, μi), если f(λi) < f(μi). Тогда в первом случае, новый интервал неопределенности имеет длину:  Отсюда следует, что в любом случае на i-той итерации интервал неопределенности сжимается в Fn-i/Fn-i+1 раз. На (i+1)-ой итерации либо λi+1 = μi, либо μi+1 = λi. Поэтому на каждом шаге вычисляется только одно новое значение функции. На (n-1)-ой итерации λn-1 = μn-1,и значение функции не вычисляется. Если ε есть точность вычисления значения функции, n – максимально возможное число вычислений функции, то конечный интервал неопределенности будет равен:  Решение. Последовательность чисел Фибоначчи имеет вид: 1,1,2,3,5,8,13,21, Итерация 1. Вычислим точки   f(λ1) = 48.8068; f(μ1) = 111.1102 Так как f(λ1) < f(μ1), то сокращаем интервал неопределенности и принимаем на 2-й итерации: a2 = a1 = 0; b2 = μ1 = 4.9231 Итерация 2. Вычислим точки   f(λ2) = 26.9131; f(μ2) = 48.8068 Так как f(λ2) < f(μ2), то сокращаем интервал неопределенности и принимаем на 3-й итерации: a3 = a2 = 0; b3 = μ2 = 3.0769 Итерация 3. Вычислим точки   f(λ3) = 24.5401; f(μ3) = 26.9131 Так как f(λ3) < f(μ3), то сокращаем интервал неопределенности и принимаем на 4-й итерации: a4 = a3 = 0; b4 = μ3 = 1.8462 Итерация 4. Вычислим точки   f(λ4) = 37.4163; f(μ4) = 24.5401 Так как f(λ4) > f(μ4), то сокращаем интервал неопределенности и принимаем на 5-й итерации: a5 = λ4 = 0.61538461538462; b5 = b4 = 1.8462 Все вычисления сведены в таблицу. Вычисления продолжаются, пока не найдены 6 новых точек.
Вычисляем точку минимума функции  f(xmin) = 24.5401 Ответ: x = 1.2308; F(x) = 24.5401 Количество итераций, N = 6 |