Лабораторная работа4 Средства поиска решения в ms excel Цель работы
 Скачать 167 Kb. Скачать 167 Kb.
|
|
Лабораторная работа№4: Средства поиска решения в MS Excel Цель работы: освоение специального инструментария MS Excel для решения оптимизационных задач. Порядок работы: Ознакомиться с механизмом поиска решения в Excel. Выполнить задание для самостоятельной работы. Ответить на контрольные вопросы. Ежедневно специалисты в области экономики и менеджмента сталкиваются с задачами оптимизации. Наиболее легкими и показательными являются задачи линейной оптимизации. Типы задач оптимизации: Задачи о перевозках: например, минимизация расходов по доставке товаров с нескольких фабрик в несколько магазинов с учетом спроса; Задачи распределения рабочих мест: например, минимизация расходов на содержание штата с соблюдением требований, определенных законодательством; Управление ассортиментом товаров: извлечение максимальной прибыли с помощью варьирования ассортиментным набором товаров (при соблюдении требований клиентов). Аналогичная задача возникает при продаже товаров с разной структурой затрат, рентабельностью и показателями спроса. Замена или смешивание материалов: например. Манипуляция материалами с целью снижения себестоимости, поддержания необходимого уровня качества и соблюдения требований потребителей. Задачи линейной алгебры: решение линейных уравнений. Для решения такого вида задач существует инструмент «Поиск решения». Процедуру поиска решения можно использовать для определения значения влияющей ячейки, которое соответствует экстремуму зависимой ячейки — например, расходы на рекламу, обеспечивающие максимальную прибыль. Влияющая и целевая ячейки должны быть связаны формулой, иначе при изменении значения одной не будет изменяться другая. Задачи, решаемые с помощью оптимизатора, имеют три характерных признака: Имеется единственная целевая ячейка. В нее пользователь должен ввести формулу, указав позднее в программном диалоге какой экстремум необходим (максимум или минимум). После завершения построения модели и инициализации расчета программа автоматически должна добиться для этой ячейки экстремального результата. В формуле целевой ячейки должны быть сделаны ссылки на одну или более изменяемых ячеек, от значений которых зависит результат. Они могут быть названы также неизвестными или переменными для решения. Поиск решения устанавливает значения изменяемых ячеек так, чтобы найти для формулы целевой ячейки оптимальное решение. Ограничивающих ячеек может быть не менее одной на каждую изменяемую ячейку. Может существовать и некоторое количество дополнительных ячеек ограничений, например, ограничение по объему ресурса и ограничения по спросу (минимальный спрос, максимальный спрос). Пример 1 . Для производства столов и шкафов мебельная фабрика использует необходимые ресурсы. Нормы затрат ресурсов на одно изделие данного вида, прибыль от реализации одного изделия и общее количество имеющихся ресурсов каждого вида приведены в следующей таблице:
Определить, сколько столов и шкафов фабрике следует изготовлять, чтобы прибыль от их реализации была максимальной. Подготовка исходных данных для решения задачи 1.Формализация задачиДля решения этой задачи необходимо построить математическую модель. Процесс построения модели можно начать с ответа на следующие три вопроса: Для определения каких величин строится модель? В чем состоит цель, для достижения которой из множества всех допустимых значений переменных выбираются оптимальные? Каким ограничениям должны удовлетворять неизвестные? В нашем случае мебельной фабрике необходимо спланировать объем производства столов и шкафов так, чтобы максимизировать прибыль. Поэтому переменными являются: x1 – количество столов, х2 – количество шкафов. Суммарная прибыль от производства столов и шкафов равна z = 6*x1 + 8*x2. Целью фабрики является определение среди всех допустимых значений х1 и х2 таких, которые максимизируют суммарную прибыль, т.е. целевую функцию z. Перейдем к ограничениям, которые налагаются на х1 и х2. Объем производства шкафов и столов не может быть отрицательным, следовательно: Нормы затрат древесины на столы и шкафы не может превосходить максимально возможный запас данного исходного продукта, следовательно: Кроме того, ограничение на трудоемкость не превышает количества затрачиваемых ресурсов Таким образом, математическая модель данной задачи имеет следующий вид: Максимизировать при следующих ограничениях: Заметим, что данная модель является линейной, т.к. целевая функция и ограничения линейно зависят от переменных. 2.Поиск решенияРешим данную задачу с помощью команды Поиск решения (Tools, Solver). Средство поиска решений является одной из надстроек Excel. Если в меню Сервис(Tools) отсутствует команда Поиск решения (Solver), то для ее установки необходимо выполнить команду Сервис -> Надстройки -> Поиск решения (Tools ->Add-ins -> Solver). Отведем ячейки А3 и В3 под значения переменных х1 и х2 (рис. 1). В 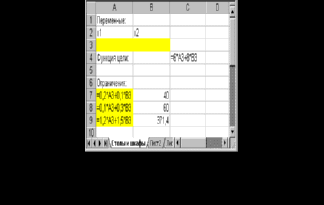 ячейку С4 введем функцию цели: =6*А3+8*В3, в ячейки А7:А9 введем левые части ограничений: ячейку С4 введем функцию цели: =6*А3+8*В3, в ячейки А7:А9 введем левые части ограничений:=0,2*А1+0,1*В3 =0,1*А3+0,3*В3 =1,2*А3+1,5*В3, а в ячейки В7:В9 – правые части ограничений. 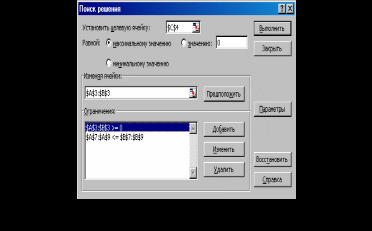 Теперь выберем команду Сервис, Поиск решения (Tools, Solver) и заполним открывшееся диалоговое окно Поиск решения (Solver), как показано на рис. 2. Не забудьте в диалоговом окне Параметры поиска решения (Solver Options) установить флажок Линейная модель (Assume Linear Model). После нажатия кнопки Выполнить (Solve) открывается окно Результаты поиска решения (Solver Results), которое сообщает, что решение найдено:  Рис. 3. Диалоговое окно Результаты поиска решения Результаты расчета задачи представлены на рис. 4, из которого видно, что оптимальным является производство 102 столов и 166 шкафов. Этот объем производства принесет фабрике 1940 руб. прибыли. 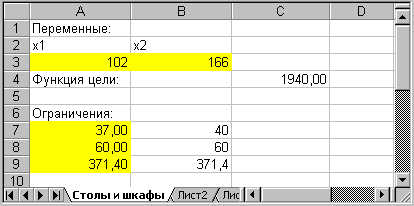 Рис. 4. Результаты расчета с помощью средства поиска решений для задачи максимизации выпуска столов и шкафов Задание для самостоятельной работыВариант1 Для производства двух видов изделий А и В используется токарное, фрезерное и шлифовальное оборудование. Нормы затрат времени для каждого из типов оборудования на одно изделие данного вида приведены в таблице. В ней же указан общий фонд рабочего времени каждого из типов оборудования, а также прибыль от реализации одного изделия.
Найти план выпуска изделий вида А и В, обеспечивающий максимальную прибыль от их реализации. Задание для самостоятельной работыВариант2 На звероферме могут выращиваться черно-бурые лисицы и песцы. Для обеспечения нормальных условий их выращивания используется три вида кормов. Количество корма каждого вида, которое должны ежедневно получать лисицы и песцы, приведено в таблице. В ней же указаны общее количество корма каждого вида, которое может быть использовано зверофермой, и прибыль от реализации одной шкурки лисицы и песца. Найти оптимальное соотношение количества кормов и численности поголовья лис и песцов.
Задание для самостоятельной работыВариант3 Для изготовления различных изделий А, В и С предприятие использует три различных видов сырья. Нормы расхода сырья на производство одного изделия каждого вида, цена одного изделия А, В и С, а также общее количество сырья каждого вида, которое может быть использовано предприятием, приведены в таблице:
Изделия А, В и С могут производится в любых соотношениях (сбыт обеспечен), но производство ограничено выделенным предприятию сырьем каждого вида. Составить план производства изделий, при котором общая стоимость всей произведенной предприятием продукции является максимальной. Задание для самостоятельной работыВариант4 На швейной фабрике для изготовления четырех видов изделий может быть использована ткань трех артикулов. Нормы расхода тканей всех артикулов на пошив одного изделия приведены в таблице. В ней же указаны имеющиеся в распоряжении фабрики общее количество тканей каждого артикула и цена одного изделия данного вида. Определить, сколько изделий каждого вида должна произвести фабрика, чтобы стоимость изготовленной продукции была максимальной.
Задание для самостоятельной работыВариант 5 Фабрика "GRM pie" выпускает два вида каш для завтрака — "Crunchy" и "Chewy". Используемые для производства обоих продуктов ингредиенты в основном одинаковы и, как правило, не являются дефицитными. Основным ограничением, накладываемым на объем выпуска, является наличие фонда рабочего времени в каждом из трех цехов фабрики. Управляющему производством Джою Дисону необходимо разработать план производства на месяц. В приведенной ниже таблице указаны общий фонд рабочего времени и число человеко-часов, требуемое для производства 1 т продукта.
Доход от производства 1 т "Crunchy" составляет 150 ф. ст., а от производства "Chewy" — 75 ф. ст. На настоящий момент нет никаких ограничений на возможные объемы продаж. Имеется возможность продать всю произведенную продукцию. Требуется: сформулировать модель линейного программирования, максимизирующую общий доход фабрики за месяц и реализовать решение этой модели. Задание для самостоятельной работыВариант6 Оливер А. Петерс скоро выйдет на пенсию, и ему предстоит решить, как поступить с единовременным пособием, которое в соответствии с пенсионной программой будет предоставлено ему фирмой. М-р Петерс и его супруга намерены предпринять длительный визит в Австралию к своей дочери сроком на два года, поэтому любые сделанные в настоящий момент инвестиции будут свободны для использования на данный период. Очевидно, цель м-ра Петерса состоит в максимизации общего дохода от вложений, полученного за двухлетний период. Мистера Петерса проконсультировали, что наилучшим вариантом вложения инвестиций был бы инвестиционный фонд, и в настоящее время он рассматривает возможность помещения инвестиций в один из таких фондов, состоящий из инвестиций трех типов — А, В и С. Сумма единовременного пособия составит 25000 ф. ст., однако, мистер Петере считает, что нет необходимости вкладывать в данный инвестиционный фонд все деньги; часть из них он намерен перевести на свой счет жилищно-строительного кооператива, который гарантирует ему 9% годовых. По мнению бухгалтера фирмы, мистеру Петерсу следует попытаться распределить свои инвестиции таким образом, чтобы обеспечить как получение дохода, так и рост капитала. Поэтому ему посоветовали не менее 40% от общей суммы вложить в вариант А и перевести на свой счет. Для обеспечения значительного роста капитала не менее 25% общей суммы денежных средств, вложенных в инвестиционный фонд, необходимо поместить в проект В, однако, вложения в В не должны превышать 35% общего объема вложений в инвестиционный фонд ввиду высокой вероятности риска, соответствующей проекту В. Кроме того, для сохранности капитала в проекты А и С следует вложить не менее 50% средств, помещаемых в инвестиционный фонд. В настоящее время проект А позволяет получать 10 % годовых и обеспечивает 1% роста капитала; проект В предполагает рост капитала в 15%; проект С дает 4% годовых и 5%-ный рост капитала. Требуется: учитывая цель м-ра Петерса, сформулировать модель линейного программирования, показывающую, как следует распределить сумму единовременного пособия между различными проектами инвестиций. Задание для самостоятельной работыВариант7 Китайская компания с ограниченной ответственностью по производству гусеничных механизмов выпускает пять сходных друг с другом товаров — А, В, С, D и Е. В нижеследующей таблице представлены расходы ресурсов, необходимых для выпуска единицы каждого товара, а также недельные запасы каждого ресурса и цены продажи единицы каждого продукта.
Известны также издержки, связанные с использованием каждого вида ресурсов: сырье — 2,10 ф. ст. за 1 кг; сборка —. 3,00 ф. ст. за 1 ч; обжиг — 1,30 ф. ст. за 1 ч; упаковка — 8,00 ф. ст. за 1 ч. Требуется: Сформулировать задачу линейного программирования таким образом, чтобы в качестве переменных как целевой функции, так и ограничений выступали ресурсы. Кратко сформулировать предпосылки применения модели. Для максимизации элементов, составляющих прибыль за неделю, следует использовать компьютерный пакет прикладных программ. Задание для самостоятельной работыВариант8 Нефтяная компания "РТ" для улучшения эксплуатационных качеств и снижения точки замораживания дизельного топлива, которое она производит, добавляет в него определенные химикаты. В каждом бензобаке объемом 1000 л должно содержаться не менее 40 мг химической добавки X, не менее 14 мг химической добавки Y и не менее 18 мг химической добавки Z. Необходимые химические добавки в форме готовых смесей поставляют "РТ" две химические компании А и В. В нижеследующей таблице приведено содержание химических добавок в каждом продукте, поставляемом указанными компаниями.
Стоимость продукта А — 1,50 ф. ст. за 1 л, а продукта В — 3,00 ф. ст. за 1 л. Требуется: найти ассортиментный набор продуктов А и В, минимизирующий общую стоимость добавленных в топливо химикатов. Задание для самостоятельной работыВариант9 Администрация компании "Nemesis Company", осуществляя рационализаторскую программу корпорации, приняла решение о слиянии двух своих заводов в Аббатсфилде и Берчвуде. Предусматривается закрытие завода в Аббатсфилде и за счет этого — расширение производственных мощностей предприятия в Берчвуде. На настоящий момент распределение рабочих высокой и низкой квалификации, занятых на обоих заводах, является следующим:
В то же время после слияния завод в Берчвуде должен насчитывать 240 рабочих высокой и 320 рабочих низкой квалификации. После проведения всесторонних переговоров с привлечением руководителей профсоюзов были выработаны следующие финансовые соглашения: 1. Все рабочие, которые попали под сокращение штатов, получат выходные пособия следующих размеров: Квалифицированные рабочие - 2000 ф. ст.; Неквалифицированные рабочие - 1500 ф. ст. 2. Рабочие завода в Аббатсфилде, которые должны будут переехать, получат пособие по переезду в размере 2000 ф. ст. 3. Во избежание каких-либо преимуществ для рабочих Берчвудского завода доля бывших рабочих завода в Аббатсфилде на новом предприятии должна совпадать с долей бывших рабочих Берчвудского завода. Требуется: Построить модель линейного программирования, в которой определяется, как осуществить выбор работников нового предприятия из числа рабочих двух бывших заводов таким образом, чтобы минимизировать общие издержки, связанные с увольнением и переменой места жительства части рабочих. В процессе формализации следует использовать следующие переменные: S1 — число квалифицированных рабочих, переведенных на новую работу с завода в Аббатсфилде; S2 — число квалифицированных рабочих, переведенных на новую работу с завода в Берчвуде; Ui — число неквалифицированных рабочих, переведенных на новую работу с завода в Аббатсфилде; U2 — число неквалифицированных рабочих, переведенных на новую работу с завода в Берчвуде. Задание для самостоятельной работыВариант10 Компания "Bermuda Paint" — частная промышленная фирма, специализирующаяся на производстве технических лаков. Представленная ниже таблица содержит информацию о ценах продажи и соответствующих издержках производства единицы полировочного и матового лаков.
Для производства 1 галлона матового лака необходимо затратить 6 мин трудозатрат, а для производства одного галлона полировочного лака — 12 мин. Резерв фонда рабочего времени составляет 400 чел.-ч. в день. Размер ежедневного запаса необходимой химической смеси равен 100 унциям, тогда как ее расход на один галлон матового и полировочного лаков составляет .0,05 и 0,02 унции соответственно. Технологические возможности завода позволяют выпускать не более 3000 галлонов лака в день. В соответствии с соглашением с основным оптовым покупателем компания должна поставлять ему 5000 галлонов матового лака и 2500 Галлонов полировочного лака за каждую рабочую неделю (состоящую из 5 дней). Кроме того, существует профсоюзное соглашение, в котором оговаривается минимальный объем производства в день, равный 2000 галлонов. Администрации данной компании необходимо определить ежедневные объемы производства каждого вида лаков, которые позволяют получать максимальный общий доход. Требуется: Построить и решить линейную модель для производственной проблемы, с которой столкнулась компания. Для исходной задачи (не учитывающей сверхурочные работы) определить промежуток изменений показателя единичного дохода за 1 галлон полировочного лака, в котором исходное оптимальное решение остается прежним. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
