Лекция 7 (1). Лекции Понятие динамического равновесия и его значение для теоретического анализа экономического роста
 Скачать 129.61 Kb. Скачать 129.61 Kb.
|
|
ТЕМА: ЭКОНОМИЧЕСКИЙ РОСТ И ДИНАМИЧЕСКОЕ РАЗВИТИЕ В ЭКОНОМИКЕ Вопросы лекции Понятие динамического равновесия и его значение для теоретического анализа экономического роста. Неокейнсианские модели равновесного экономического роста: модели Е. Домара и Р. Харрода. Модель равновесного экономического роста Р. Солоу. Задачи потребительского и производственного выбора в модели Рамсея. Эндогенный экономический рост и модель перекрывающихся поколений. Модель Ромера. 6. Дилемма государственной политики регулирования экономического роста в динамически эффективной экономике. Понятие динамического равновесия и его значение для теоретического анализа экономического роста. Равновесие экономической системы — это состояние, при котором согласованность основных пропорций в экономике обеспечивает непрерывность процесса воспроизводства в неизменных или возрастающих масштабах. Экономической наукой выделяется пять основных пропорций в экономике, согласование которых обеспечивает достижение сбалансированности: факторная пропорция (производственные, трудовые, финансовые ресурсы), связывающая объем, структуру и производительность ресурсов с объемом и структурой производства материальных благ и услуг; пропорция накопления, определяющая норму накопления, т.е. ту долю в национальном доходе страны, которая должна пойти на расширение производства для получения определенного его объема; пропорция распределения, определяющая соотношение в распределении доходов от производственной деятельности между всеми владельцами факторов производства; пропорция обмена (реализации), определяющая соотношение между потребительным спросом и предложением по объему, структуре и стоимости; товарно-денежная пропорция, выражающая соотношение между товарной и денежной массами. В директивно-плановой системе хозяйствования ведущей была факторная пропорциональность. К ней приспосабливались все остальные. В рыночной экономике ведущей является пропорция обмена. Это объясняется определяющим влиянием спроса на развитие рыночного хозяйства. Достижение равновесия между спросом и предложением служит одним из основных показателей эффективности функционирования экономики страны в условиях рынка. Экономическая наука различает статическое и динамическое равновесие. При статическом равновесии факторная пропорция остается неизменной, поэтому равновесие в экономике определяется соотношением всех остальных пропорций. При статическом подходе оптимальное равновесие достигается при полном использовании производственных возможностей. Экономическая система, способная достичь такого равновесия, признается статически эффективной. При динамическом равновесии экономическая система развивается в условиях изменяющихся производственных ресурсов. Динамическое равновесие — это состояние экономики, при котором динамика производственных возможностей и динамика пропорций экономической системы достигают соотношения, обеспечивающего постоянный темп экономического роста. Экономика, способная поддерживать устойчивый экономический рост, признается экономической наукой динамически эффективной. Можно выделить три типа динамического равновесия: при растущей производительности ресурсов; при их неизменной производительности; при снижающейся производительности ресурсов. Оптимальным динамическим равновесием признается равновесие при растущей производительности производственных ресурсов. Лишь в этом случае в длительной перспективе достигается максимальный объем производства. На первых этапах экономического анализа рыночной системы развивалась теория статического равновесия (классическая политэкономия А.Смита, Д.Рикардо и др.). Д.Кейнс и его последователи разрабатывали концепцию государственного регулирования экономики с целью повышения ее статической эффективности. Экономисты неоклассического направления, продолжая разработку теории статического равновесия, создали теорию общего равновесия, основой которой стала модель Л.Вальраса, предпринявшего попытку математического выражения пропорций статического равновесия. Во второй половине XX в. под воздействием НТР экономические системы западных стран развиваются в условиях необходимости поддержания динамического равновесия при растущей производительности производственных ресурсов. В связи с этим оптимальное статическое равновесие рассматривается экономической наукой лишь как способствующее анализу проблем экономической динамики. В условиях растущей производительности производственных ресурсов экономическая система лишена устойчивости, и поддержание динамического равновесия практически не решается ни рынком, ни государственным регулированием. Кейнсианская теория (центральное место в которой занимает эффективный спрос) стремится определить такие условия, при которых изменения величины совокупного спроса во времени соответствовали бы тренду потенциального ВВП. В этом случае в экономике будет наблюдаться динамически устойчивое равновесие в долгосрочном периоде. Величина выпуска в долгосрочном периоде, с одной стороны, определяется количеством имеющихся ресурсов (в двухфакторной модели – количеством труда и капитала), а экономический рост, происходит за счет количественного расширения ресурсного потенциала экономики, является экстенсивным. В неокейнсианских моделях экономический рост исследуется с помощью инструментов и методов анализа кейнсианской школы, примененных к динамическим процессам. Напомним, что под динамическим равновесием понимается равенство темпов прироста совокупного спроса и совокупного предложения. Поэтому модели, исследующие достижение и характер такого равенства, называются динамическими. В динамических моделях, в отличие от статических, критерием краткосрочности или долгосрочности периода является изменение технологии производства. Краткосрочный динамический период характеризуется неизменностью технологии, которая может сохраняться в предыдущем, текущем и будущем периодах при варьирующих темпах реального ВВП. Соответственно, в долгосрочном динамическом плане меняется сам технологический уровень производства. 2. Неокейнсианские модели равновесного экономического роста: модели Е. Домара и Р. Харрода. В современной экономической теории под теорией экономического роста имеется в виду формальная теория роста, возникшая как результат распространения кейнсианства на долгосрочный (по Маршаллу) период. Начало этой теории положили модели английского экономиста Роя Харрода и американца Евсея Домара. С другой стороны, на экономический рост влияет научно-технический прогресс, а экономический рост, происходит за счет качественного улучшения ресурсного потенциала экономики, является интенсивным. Существует несколько вариантов записи модели Харрода, принадлежащих и ему самому, и последующим экономистам. Но во всех случаях модель состоит из трех частей. 1. Фундаментальное уравнение роста. Прежде всего из дефиниций основных экономических агрегатов и тождественных преобразований выводится фундаментальное уравнение Харрода 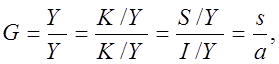 (1) (1)где G— темп прироста дохода или выпуска продукции, Y — доход или выпуск продукции. К— капитал, S— сбережения, I — инвестиции, по определению равные приросту капитала К, по условию равные сбережениям; s - доля сбережений в доходе; а - коэффициент приростной капиталоемкости (количество капитала, необходимое для увеличения выпуска на единицу). В этой форме фундаментальное уравнение представляет собой достаточно тривиальный вывод: темп роста прямо пропорционален доле сбережений и обратно пропорционален капиталоемкости. Однако ему можно придать и более содержательную интерпретацию с точки зрения исследуемой проблемы стабильности экономического роста. Гарантированный рост. Инвестиции в каждый период времени t зависят от ожидаемого для данного периода прироста выпуска: It=asY*t, (2) где It, - инвестиции в период t, Y*t - ожидаемый доход, a - коэффициент приростной капиталоемкости (количество капитала, необходимое для увеличения выпуска на единицу). Данное равенство фактически представляет собой механизм акселератора. В то же время сбережения для того же периода по определению равны: St=sY*t, (3) где Yt — доход или выпуск продукции в период t, St — сумма сбережений в этот же период, s — доля сбережений в доходе По условию St = It, т.е. sYt = a s Y*t (4) Теперь нас интересует ситуация, которая является необходимым условием сбалансированного роста. Это ситуация, когда ожидания предпринимателей выполняются и у них, следовательно, нет никакого стимула расширять или сокращать свои производственные мощности. (Предполагается, что при исполнении желаний мощности загружены полностью.) В этом случае ожидаемый прирост дохода должен быть равен фактическому: s Y*t = s Yt, т.е. предприниматели не сталкиваются ни с какими приятными или неприятными сюрпризами. 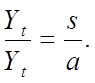 (5) (5)Тогда из уравнения (4) следует, что (5) Левая часть уравнения (5) — это тоже темп прироста дохода (или продукта), но не любой, а такой, при котором планы предпринимателей в точности реализуются. Харрод назвал такой рост гарантированным (warranted, или С), хотя логичнее, вероятно, было бы назвать его «равновесным». Величина а в правой части уравнения (5) тоже представляет собой не любой коэффициент приростной капиталоемкости, а только тот, который требуется для гарантированного роста. Ее поэтому можно записать как аr (индекс r обозначает требуемый (англ. required) уровень данного показателя). «Это новый (предельный) капитал, требуемый для сохранения такого выпуска продукции, который должен удовлетворить потребительский спрос, возникающий из предельного добавочного дохода потребителей». В каждый данный момент Харрод рассматривает величину аr как фиксированную. Это означает, что замещение труда капиталом или, наоборот, в процессе производства он считает невозможным. Данную предпосылку, которая, как мы увидим ниже, играет в его модели решающую роль, Харрод выводит не из постоянства технологий, как можно было бы предположить, а из предполагаемой жесткости цен труда и капитала — ставки заработной платы и нормы прибыли. Гибкость первой ограничена закрепленной в обществе минимальной ставкой зарплаты, а гибкость второй — минимально приемлемым уровнем процента. Таким образом, стабильный гарантированный рост равен: 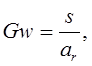 (6) (6)и для каждого момента его величина определена однозначно. Фактический рост вовсе не обязательно должен быть равен гарантированному, хотя, конечно, всякий предприниматель стремится к тому, чтобы его планы были максимально точными. Расхождение же этих величин в модели Харрода имеет тенденцию не сглаживаться, а, напротив, нарастать, что ведет к неустойчивости системы. Так, если G > Gw, т.е. рост оказался больше ожидаемого, то капиталоемкость а будет меньше требуемой аr. Это приведет в действие эффект акселератора — возрастут заказы на инвестиционные товары. В свою очередь инвестиционный мультипликатор приведет к дальнейшему росту производства. Если же фактический рост окажется меньше гарантированного (ожидания производителей окажутся недовыполненными), то мощности окажутся недогруженными, что запустит механизм акселератора-мультипликатора в сторону понижения. Возрастающее отклонение фактического роста от гарантированного можно было бы предотвратить, если бы норма сбережения s изменилась во столько же раз, что и фактический темп роста G, но в противоположном направлении. Однако, как справедливо отмечает Харрод, нельзя представить себе, что доля сбережений в доходе должна увеличиться в 4 раза вследствие того, что темп роста дохода изменился с 1 до 4%. Таким образом, ситуация сбалансированного роста, когда фактический рост равен гарантированному, оказывается, говоря словами Харрода, «равновесием на лезвии ножа». Действием этих центробежных сил, заставляющих систему отклоняться все дальше от равновесного роста, Харрод объяснял феномен экономического цикла. Сам Харрод пишет, что Gw есть величина, определяемая время от времени опытным путем и посредством проб и ошибок, совершаемых великим множеством людей. Было бы большой удачей, если бы в результате их коллективных оценок им удавалось точно достигать величины Gw. Следует оговориться, что модель Харрода учитывает только эндогенные инвестиции, порождаемые акселерационным механизмом, и абстрагируется от автономных инвестиций, вызванных к жизни новыми изобретениями, долгосрочными ожиданиями и пр. Естественный рост. Если гарантированный рост гарантировал полную загрузку производственных мощностей, то далее Харрод вводит в свой анализ предпосылку полной занятости другого фактора производства — трудовых ресурсов. Темп экономического роста при полной занятости труда Харрод назвал естественным — Gn (индекс п соответствует английскому слову natural), хотя, может быть, правильнее было бы назвать его «максимальным». Он определяется темпом роста предложения труда и темпом роста его производительности. При предпосылке экспоненциального роста предложения и производительности труда естественный темп роста равен сумме темпов роста этих величин Gn = п + g, (7) где п — темп роста предложения труда, g — темп роста производительности труда Gn - максимально возможный уровень среднего значения G за долгосрочный период. Для того чтобы были полностью загружены и труд и капитал, должно соблюдаться равенство Gw = Gn. Однако гарантированный и естественный темпы роста определяются независимо друг от друга совершенно разными факторами, и совпасть могут только случайно. «Лезвие ножа», на котором находится равновесие в модели Харрода, оказывается «обоюдоострым» — необходимо дополнительно рассмотреть случаи неравенства Gw и Gn. Для начала, предположим, что Gw < Gn. Выше было сказано, что если G > Gw, возникает самоподдерживающийся бум. Если же при этом к тому же Gw < Gn, т.е. Gw < G < Gn, то этому буму не видно никаких границ в долгосрочном периоде. Структурная безработица присутствует, так как уровень Gn не достигнут, но сокращается. Однако это состояние нельзя назвать беспроблемным, поскольку ситуация, когда производственные мощности хронически перегружены, чревата инфляцией. Конечно, намного хуже, если Gw > Gn. Тогда G просто не может быть больше Gw (G < Gn< Gw), так как величина Gn — его физический предел. Это означает одновременное существование безработицы (G< Gn) и недогрузки мощностей (Gn < Gw), т.е. преимущественно депрессивное состояние хозяйства в течение долгого времени. Таким образом, если расхождение фактического и гарантированного роста создает циклические колебания, то расхождение гарантированного и естественного роста ведет к хронической безработице. Модель Харрода иллюстрирует циклическую и долгосрочную нестабильность капиталистической экономики. В своих статьях 1946— 1947 гг. американский экономист Евсей До-мар, не знавший о работе Харрода 1939 г., самостоятельно пришел к уравнению равновесного роста, аналогичного уравнению гарантированного роста Харрода. Основная идея Домара заключалась в том, что инвестиции играют в экономике двойственную роль: с одной стороны, они создают производственные мощности, а с другой — создают спрос через эффект мультипликатора. Домар показал: для того, чтобы прирост спроса соответствовал приросту мощностей, инвестиции (а значит — при условии равновесного роста и весь национальный доход) должны расти темпом, равным os, где о — показатель капиталоотдачи, as— норма сбережений. Поэтому в теории экономического роста принято говорить о модели Харрода—Домара. В период времени tYt= LtPt, где L — предложение труда, а Р— производительность труда. Если величина L растет неизменным темпом п процентов, а Р- неизменным темпом процентов, то Lt= Lyent, a Pt= Pegt. Подставив два последних выражения в первое уравнение, прологарифмировав и продифференцировав, получим приведенный в тексте результат. 3. Модель равновесного экономического роста Р. Солоу. После второй мировой войны теория роста стала развиваться в ином по сравнению с довоенной депрессией контексте. 1950-е годы стали периодом устойчивого роста. В США бум был связан с Корейской войной, в Западной Европе и в Японии — с американской помощью по плану Маршалла. Так или иначе, стало ясно, что модель Харрода—Домара сильно преувеличивала неустойчивость западной экономики и недооценивала силы, ведущие к ее росту. С середины 1950-х годов начался новый этап развития теории роста, который продолжался примерно до середины 1970-х, когда на авансцену вышла теория цикла. Ключевую роль на этом этапе сыграла модель роста Р. Солоу. Солоу пришел к выводу, что основной причиной неустойчивости экономики в модели Харрода—Домара является фиксированная величина капиталоемкости (а), отражающая жесткое соотношение между факторами производства — трудом и капиталом (K/L). Неудивительно, что в этом случае один из этих факторов часто остается «недогруженным». В соответствии же с принципами неоклассической теории пропорции между капиталом и трудом должны быть переменными (именно в этом заключается неоклассический характер теории роста Солоу). Они определяются минимизирующими издержки производителями в зависимости от цен на эти факторы производства. Поэтому вместо фиксированного K/L Солоу включил в свою модель линейно-однородную производственную функцию: Y= F(K, L). (8) Разделив все члены на L и обозначив доход на одного работника (Y/L) через у, а капиталоинтенсивность K/L через k, получим: y=LF(k,l)=Lf(k) (9) Как и в модели Харрода—Домара, предполагается, что население растет неизменным темпом я, а инвестиции составляют постоянную долю дохода, определяемую нормой сбережения у. I=sY. Темп прироста k тогда можно записать как Это так называемое «фундаментальное уравнение» Солоу словами выражается так: прирост капиталовооруженности одного работника — это то, что осталось от удельных инвестиций (сбережений), после того как удалось обеспечить капитальными благами всех дополнительных работников. Если sf(k) == nk, то капиталовооруженность остается прежней (dk = 0), т.е. экономика растет без каких-либо структурных изменений в соотношении между факторами. Это и есть сбалансированный рост. В модели Солоу в противоположность модели Харрода—Домара траектория сбалансированного роста является устойчивой. Солоу показывает это с помощью следующего графика (рис. 1). 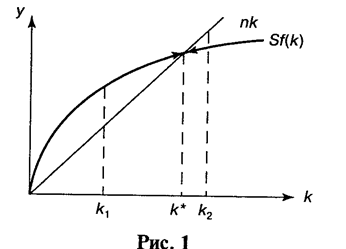 Рис. 1. Инвестиции, выбытие и устойчивый уровень капиталовооруженности Прямая nk на этом графике показывает, сколько каждый работник должен сберегать и инвестировать из своего дохода, чтобы обеспечить будущих работников (в том числе своих собственных детей) капитальными благами. Кривая sf(k) демонстрирует, каковы его фактические сбережения в зависимости от достигнутого уровня капиталовооруженности. С ростом капиталовооруженности А; темп роста инвестиций/сбережений, естественно, падает. Вертикальное расстояние между кривой и прямой обозначает в соответствии с фундаментальным уравнением Солоу дифференциальное изменение показателя капиталовооруженности dk. В точке k* оно равно нулю и наблюдается сбалансированный рост. Во всех точках левее k* (например, k^) капиталовооруженность будет расти, а во всех точках правее k* (например, k.) падать, так что экономика постоянно сдвигается в сторону k* и траектория сбалансированного роста является устойчивой. В модели Солоу норма сбережений s имеет значение только до выхода экономики на траекторию устойчивого развития: чем больше величина s, тем выше график skn соответственно уровень k*. Но как только рост стал сбалансированным, его дальнейший темп зависит только от роста населения и технологического прогресса. «Золотое правило». Из модели Солоу следовало, что чем больше норма сбережений, тем выше капиталовооруженность работника в состоянии сбалансированного роста и, следовательно, тем выше темп сбалансированного роста. Но сам по себе рост не является самоцелью. Поэтому следующим шагом, логически вытекающим из модели, было определение условий оптимального для общества экономического роста. Этот шаг одновременно и независимо друг от друга сделали несколько экономистов (Т. Суон, Дж. Мид, М. Алле, Дж. Робинсон, К. фон Вайцзеккер и др.) в самом начале 1960-х годов. Но первым опубликовал ответ на данный вопрос американский экономист Эдмунд Фелпс. Ему же принадлежит и термин «золотое правило накопления капитала», вошедший с тех пор в широкое употребление. Фелпс задался вопросом, какой величины капитал захочет иметь общество, находящееся на траектории сбалансированного роста. Если он будет достаточно большим, это гарантирует высокий уровень производства, но все большая его часть пойдет не на потребление, а на накопление — общество не сможет насладиться плодами роста. Если же объем капитала будет слишком малым, то потреблять можно будет почти все, что произведено. Где-то посредине между этими двумя крайностями, очевидно, находится оптимальная для общества точка, в которой объем потребления общества является максимальным. Это можно следующим образом показать на графике (рис. 2). 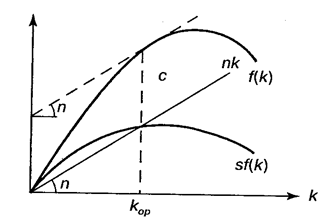 Рис. 2 Рис. 2. Золотое правило накопления в условиях технологического прогресса К графику на рис. 1 мы добавим кривую выпуска или дохода на душу населения у =f(k). Тогда максимизироваться будет вертикальное расстояние между кривой дохода на душу населения и инвестиций на душу населения: f(k) — sf(k) =f(k) — nk (в случае сбалансированного роста). Это расстояние является максимальным в точке, где угол наклона касательной к кривой/(А;) равен углу наклона прямой nk, т.е. п. Это задает оптимальный уровень капиталоинтенсивности. Остается выбрать такую норму потребления/накопления, чтобы кривая sf(k) пересекала луч nk в точке, соответствующей k. Если мы далее (вместе с перечисленными выше авторами, но за исключением Фелпса) предположим, что в нашей экономике существует совершенная конкуренция на рынках факторов производства и, следовательно, действует теория предельной производительности, то угол наклона (предельная производительность капитала) должен быть равен ставке процента г. В этом случае «золотое правило» можно сформулировать так: ставка процента должна быть равна темпу роста населения, а значит (при сбалансированном росте), и всей экономики: r = п (11) Следовательно, в экономике, испытывающей бурный рост, ставки процента должны при прочих равных условиях быть высокими. Применимость «золотого правила» на практике оказалась весьма ограниченной ввиду достаточно сильных исходных предпосылок, но оно позволило сформулировать выводы, относящиеся к реальному экономическому росту. Модель Солоу и «золотое правило» оказались достаточно простыми и чрезвычайно удобными в употреблении аналитическими орудиями. С их помощью оказалось возможно исследовать влияние на экономический рост различных модификаций производственной функции, технического прогресса, изменения нормы сбережений и налогообложения и т.д. Усилиями самого Солоу, Д. Мида и других экономистов модель Солоу была дезагрегирована: отдельно учитывалось производство потребительских и инвестиционных благ. Были созданы также модели, учитывающие «возраст» капитальных благ, поскольку разные их поколения обладают разной производительностью (vintage models). Работы Джеймса Тобина ввели в теорию роста денежную массу (точнее, государственные обязательства, которыми люди владеют наряду с капиталом). 4. Задачи потребительского и производственного выбора в модели Рамсея. Модель Рамсея является естественным обобщением модели Солоу-Свена, хотя была опубликована почти на 30 лет раньше. В отличие от модели Солоу, в модели Рамсея норма сбережения определяется эндогенно рациональными домохозяйствами и фирмами, взаимодействующими на конкурентных рынках. Точнее говоря, в модели рассматриваются бесконечно живущие домохозяйства, выбирающие потребление и сбережение с целью максимизации благосостояния своего “клана” при наличии межвременного бюджетного ограничения, и фирмы, максимизирующие свою прибыль. Домохозяйства в модели обеспечивают фирм рабочей силой в обмен на з/п, получают процентные платежи по своим активам, приобретают товары для потребления и сберегают путем накопления дополнительных активов. Каждое домохозяйство состоит по крайней мере из одного взрослого и его детей. Взрослые учитывают в своих действиях интересы наследников, как живущих ныне так и тех, кому еще предстоит родиться. Это предположение отражается в модели в виде функции полезности, определенной на бесконечном временном интервале. Хотя жизнь каждого члена семьи конечна, сама семья существует бесконечно долго. Вследствие рождаемости и смертности, мы предполагаем темп роста населения постоянным и экзогенно заданным: L (t) = ent. Если C (t) — совокупное потребление в момент t, то c (t) : = C (t) /L (t) — подушевое потребление. Каждое домохозяйство стремится максимизировать свою совокупную полезность U, 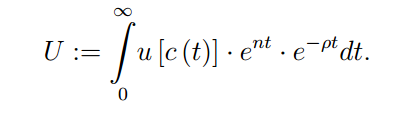 т. е. взвешенную сумму будущих “потоков полезности”, причем u’ (·) > 0 и u’’ (·) < 0. Вогнутость выражает стремление домохозяйств к сглаживанию потребления, т. е. они предпочитают относительно однородное потребление такому, где c (t) высоко в одни периоды и низко в другие. Предполагаются также выполненными условия : u’ (0) = ∞ и u’ (∞) = 0. Множитель e−ρt отражает норму межвременных предпочтений, причем ρ >0, что говорит о том, что будущая полезность ценится меньше текущей (собственная полезность ценится выше, чем полезность потомков). Предполагается, что ρ > n, т.е. U ограничена, если c (t) постоянно. Домохозяйства владеют активами в форме требований на капитал или займов. Отрицательные займы означают долги. Экономика закрытая, внешней торговли нет. Домохозяйства могут занимать друг у друга, но в целом в равновесии чистые займы будут равны нулю. Поскольку обе формы активов равносильны как способы хранения ценностей, они имеют одинаковую реальную ставку процента, r (t). Обозначим через a (t) чистые подушевые активы домохозяйства, измеренные в единицах потребления, через w (t) — ставку заработной платы. Предполагается, что каждый взрослый неэластично предлагает 1 единицу труда в каждый момент времени, так что заработанный доход на душу равен w (t). Нежелательной безработицы в модели нет. Совокупный доход на душу равен w (t) + r (t) · a (t), последнее слагаемое может быть и отрицательно. Бюджетное ограничение домохозяйства есть: a˙ = w + ra − c − na (2) (активы на душу падают с ростом населения, отсюда слагаемое na). Рынок займов в модели накладывает ограничение на сумму заимствования, так что текущая стоимость активов должна быть асимптотически неотрицательной: (3) 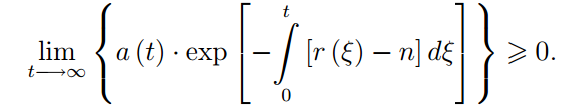 Условие означает, что в долгосрочном периоде подушевой долг (при a (t) < 0) не может расти с темпом r (t) − n, т. е. долг не может расти с темпом r (t). Задача домохозяйства заключается в максимизации полезности (1) при ограничениях (2), (3) и начальном условии на активы a (0). Ограничение c (t)>= 0 благодаря условиям связывающим не является. Фирмы производят товары, выплачивают з/п и рентные платежи на капитал. Каждая фирма обладает технологией Y = F (K, L, t) , где K — капитал, выраженный в единицах товара, L — труд, выраженный в человеко-часах в год, t отражает технологический прогресс. F (·) — неоклассиxеская функция по K и L. Далее предполагается, что F (K, L, t) = F (K, Lˆ), где Lˆ := L · A (t) — уровень эффективных трудозатрат, A (t) — уровень технологии, растущий с постоянным темпом x >= 0. Обозначая yˆ := Y/Lˆ, kˆ := K/Lˆ и f (kˆ) := F (kˆ, 1), получаем выражения для предельных продуктов факторов: 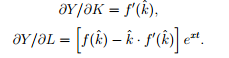 Из условий формулы следует, что f ‘ (0) = ∞ и f ‘ (∞) = 0. Предполагается, что капиталом владеют домохозяйства, а капитал и потребляемый товар полностью взаимозаменяемы. Прибыль фирмы запишется в виде:  Условие максимума прибыли для конкурентной фирмы есть f ‘ (kˆ) = r + δ. В оптимуме прибыль должна быть равна нулю, тогда ∂Y/∂L = w. Таким образом, модель не определяет индивидуальное предложение труда, зато определяет отношение факторов к затратам, а также совокупный выпуск. Таким образом, на основании рассмотрения модели Касса - Купманса-Рамсея можно сделать следующие выводы. Если предложение факторов эластично, перед домохозяйствами дополнительно возникает задача выбора оптимального временного распределения между рабочим временем и досугом. Если предложение факторов эластично, перед домохозяйствами дополнительно возникает задача выбора оптимального временного распределения между рабочим временем и досугом. Если предложение факторов эластично, перед домохозяйствами дополнительно возникает задача выбора оптимального временного распределения между рабочим временем и досугом. 5. Эндогенный экономический рост и модель перекрывающихся поколений. Модель Ромера Разочарование в традиционных неоклассических моделях усилилось в конце 1980 — начале 1990-х годов с углублением долгового кризиса и межстрановых различий в темпах роста. Традиционная теория не могла дать удовлетворительного объяснения этим явлениям. Ведь согласно ей дефицит капитала в «третьем мире» должен вести к повышенной рентабельности инвестиций. И именно на рост инвестиций была нацелена политика формирования свободного рынка, которые Всемирный банк и МВФ навязывали странам с большой внешней задолженностью. Рост инвестиций, как ожидалось, должен был вызвать рост производительности труда и уровня жизни. Однако, несмотря на предписанную либерализацию внешней торговли и внутренних рынков, многие развивающиеся страны не вышли из стагнации и не смогли привлечь новые иностранные инвестиции; им не удалось даже остановить утечку своих капиталов за рубеж. Объяснить эти явления попыталась концепция эндогенного роста (новая теория роста). Новая теория направлена на анализ эндогенного роста — постоянного увеличения ВВП, предопределенного той экономической системой, которая реально управляет общественным производством в стране. Основное отличие моделей эндогенного роста заключается в зависимости темпов прироста основных показателей национального продукта на душу населения от поведенческих и институциональных параметров. Два основных направления моделей эндогенного роста: модели, объясняющие источники роста с помощью внешних эффектов обучения на практике и человеческого капитала и мотивируя отсутствие убывающей предельной производительности. (Р. Лукас, 1988 и др.); модели, сосредоточенные на объяснении происхождения технического прогресса и детальной разработке структуры возникновения и реализации инноваций. (П. Ромер, 1990 и др.) Базовые модели эндогенного роста: А. Группа моделей, в которых представлено производство инноваций, как продукта, производимого особым сектором экономики, т.е. непосредственно процессом НИОКР (R&D). Б. Деятельность, направленная на самого человека увеличивает человеческий капитал. В. Модели обучения на практике. Г. Модели международной торговли и распространения технологий. Д. Модели технического прогресса и населения. Е. Модели неравенства и экономического роста. Ж. Модели политики и экономического роста. Модели эндогенного роста внешне похожи на неоклассические, но значительно отличаются от них исходными посылками и выводами. Прежде всего модели эндогенного роста отвергают неоклассическую посылку об убывающей предельной производительности капитала, допускают возможность эффекта масштаба производства в рамках всей экономики и просто акцентируют внимание на влиянии внешних эффектов на рентабельность капиталовложений. Хотя техническому прогрессу отводится определенная роль в этих моделях, он уже не является единственной возможной "причиной экономического роста в долгосрочном плане. Главными целями новой теории роста являются объяснение межстрановых различий в темпах роста и факторов, от которых эти темпы зависят. Важный вывод, который следует из этих положений, состоит в том, что временное или длительное торможение роста в стране ведет к ее хроническому, все более сильному отставанию от более богатых стран по уровню доходов на душу населения. Но, пожалуй, самый интересный аспект моделей эндогенного роста — объяснение противоестественного перелива капиталов из бедных стран в богатые, который усугубляет разрыв в доходах между «первым» и «третьим» мирами. Потенциально высокая рентабельность инвестиций в «третьем мире» часто сводится на нет низким уровнем комплементарных инвестиций в человеческий капитал (систему образования), инфраструктуру и НИОКР. Бедные страны извлекают из этих видов инвестиций мало выгод по сравнению с экономически развитыми странами. Отсюда следует вывод о том, что государство призвано улучшить распределение ресурсов, предоставляя за свой счет общественные товары и услуги (создавая инфраструктуру) и одновременно стимулируя частные инвестиции. Поэтому модели эндогенного роста в отличие от неоклассических выступают за активное вмешательство государстваа в процесс развития. Оставаясь во многом в русле неоклассической теории, теория эндогенного роста представляет собой шаг в сторону от догмата свободного рынка и минимальной роли государства в экономике. Модель пересекающихся (перекрывающихся) поколений (модель Даймонда, модель Самуэльсона — Даймонда, англ. overlapping generations model) — модель экзогенного экономического роста в условиях совершенной конкуренции. Внесла вклад в понимание того, каким образом решения индивидов формируют норму сбережений в экономике. В модели отражено изменение потребительского поведения индивида по мере взросления. Вместе с тем, в модели отрицаются альтруистические связи между поколениями, и она не даёт удовлетворительного объяснения межстрановым различиям в уровне дохода на душу населения. Разработана Питером Даймондом с использованием идей Пола Самуэльсона в 1965 году. В первых моделях экономического роста (модель Солоу, модель Харрода — Домара) использовались экзогенно задаваемые параметры «норма сбережений» и «темп научно-технического прогресса», от которых, в конечном итоге, и зависели темпы роста. Исследователи же хотели получить обоснование темпов экономического роста внутренними (эндогенными) факторами, поскольку модели с заданной нормой сбережений имели ряд недостатков. Они не объясняли устойчивые различия в уровнях и темпах роста между развивающимися и развитыми странами. В модели Рамсея — Касса — Купманса был преодолён недостаток экзогенности нормы сбережений. Однако она сохранила другой недостаток ранних моделей — в ней рассматривается бесконечно живущий индивид (или домохозяйство) в качестве вечного потребителя. Но по мере взросления характер потребительского поведения меняется. Если в молодом возрасте индивид работает и делает сбережения, то в старости он эти сбережения тратит. В декабре 1965 года Питер Даймонд, будущий лауреат Нобелевской премии по экономике, опубликовал работу «Национальный долг в неоклассической модели роста» в журнале The American Economic Review (англ.) русск., в которой он развил идеи Самуэльсона с учётом выводов модели Солоу и модели Рамсея — Касса — Купманса и представил модель пересекающихся поколений, также известную как модель Даймонда, модель Самуэльсона — Даймонда. В данной модели рассматривается закрытая экономика. Фирмы максимизируют свою прибыль, а потребители — полезность своих трат. Фирмы функционируют в условиях совершенной конкуренции. Производится только один продукт, используемый как для потребления , так и для производственных нужд (учитывается как инвестиции). Темпы технологического прогресса, роста населения и норма выбытия оборудования (капитала) — постоянны и задаются экзогенно. Индивидуумы живут два периода: в первом они работают, потребляют и сберегают, во втором — только потребляют, тратя накопленные в первом периоде сбережения (выходят на пенсию). Альтруистические связи между поколениями отсутствуют: молодые не помогают старикам и не получают наследство. Время изменяется дискретно. Один период в модели соответствует смене поколений, то есть в реальном выражении эквивалентен примерно 25—30 годам. Закрытость экономики означает, что произведённый продукт тратится только на сбережение и потребление, экспорт/импорт отсутствуют, инвестиции равны сбережениям. Производственная функция Y(K,L,E) удовлетворяет неоклассическим предпосылкам: технологический прогресс увеличивает производительность труда (нейтрален по Харроду); в производственной функции используются труд L и капитал K, она обладает постоянной отдачей от масштаба: Y(aK,aLE)=aY(K,LE); предельная производительность факторов положительная и убывающая; производственная функция удовлетворяет условиям Инады, а именно, если запас одного из факторов бесконечно мал, то его производительность бесконечно велика, если же запас одного из факторов бесконечно велик, то его производительность бесконечно мала; для производства необходим каждый фактор: Y(K,0)=Y(0,LE)=0; Y(K,0)=Y(0,LE)=0. Население L{t} растёт с постоянным темпом n: L{t}=(1+n)L. В каждом периоде t живёт L{t} молодых и L{t-1} пожилых индивидов. Молодой индивид предлагает одну единицу труда (предложение труда неэластично) и получает натуральную заработную плату (неким количеством единственного товара, деньги отсутствуют). Каждый индивид выбирает и разделяет полученное между потреблением в молодости или сбережением и потреблением в старости, максимизируя межвременную полезность своих трат. Модель Р. Лукаса. Делает упор на возможность постоянного экономического роста на основе постоянного персонифицированного человеческого капитала; Включает два сектора: сектор образования и сектор конечной продукции. Человеческий капитал – это оценка воплощенной в индивидууме способности приносить доход, сумма способностей, знаний, квалификации и навыков отдельного работника. Свойства человеческого капитала: зависит как от врожденных способностей и талантов, так и от полученного образования и тренинга. как и физический капитал способен накапливаться и амортизироваться Инвестиции в человеческий капитал – «деятельность, которая влияет на будущий денежный и психический доход посредством увеличения ресурсов человека». Формы инвестиций в человеческий капитал: обучение, образование; повышение квалификации; забота о здоровье: миграция поиск информации о ценах и доходах. Сектор образования представляет собой элемент экономической системы, производящей человеческий капитал в соответствии с: определенной производительностью долей времени обучения от общего объема времени каждого индивида средним уровнем имеющегося на данный момент человеческого капитала Общий объем человеческого капитала (H): H = h × L, где h – средний уровень человеческого капитала или индивидуальный уровень человеческого капитала репрезентативного агента; L – население; L = const.. Cектор конечной продукции представляет собой стандартную производственную функцию с обычными свойствами производственных функций: Y = bKα [(1 – u)H]1 – αhε где: b – параметр производительности сектора конечной продукции α – доля физического капитала в выпуске 1 – u – доля работы каждого индивидуума и соответственно общества в секторе конечной продукции h – внешний эффект от среднего уровня образования на производство конечной продукции ε – коэффициент эластичности конечного производства по среднему уровню человеческого капитала Накопление физического капитала рассчитывается по стандартным условиям тождества национальных счетов: ∆ K = Y – C Продуктом сектора образования является прирост индивидуального уровня человеческого капитала: ∆h = γ × u × h, где γ – коэффициент производительности сектора образования, константа; u – доля времени обучения в общем объеме времени h – уровень образования Выводы: Выводы: в модели проводится максимизация долгосрочного уровня потребления при оптимальном накоплении физического и человеческого капитала соответственно оптимальной доле времени, отведенной потребителем каждому сектору, постоянный устойчивый рост с зависимостью от человеческих параметров возможен на основе накопления персонифицированного человеческого капитала, таким образом, накопление человеческого капитала может быть источником устойчивого экономического роста. Модель П. Ромера (общая характеристика) показывает возможность существования устойчивого роста с постоянным темпом прироста на основе внедренного технического прогресса (эндогенного роста); производство делится на производство конечного и промежуточного продукта; технический прогресс выражается в расширении видов производственных (промежуточных) продуктов (горизонтальный тип технического прогресса), каждый из которых упрощенно идентифицируется с определенной технологией; источником покрытия затрат на НИОКР (research and development) выступает монопольная прибыль производителя промежуточного продукта, для получения которой он проводит финансирование исследований. Физический капитал в модели равен сумме промежуточных товаров, каждый из которых полностью используется в одном производственном цикле и отождествлен с определенной технологией При условии симметрии относительно всех типов промежуточных продуктов физический капитал находится умножением их числа на их количество каждого из них: K = N × x Производственная функция конечного продукта при условии симметрии выражается как функция вида Кобба — Дугласа Y = AL1 - α Nxα = Kα L1 - α N 1 - α Инвестиции в соответствии с тождеством национальных счетов: ∆ K = Y – C Цена единицы выпуска конечного продукта Y-p для простоты в модели равна единице. Сектор конечной продукции выражен стандартно и работает при условии совершенной конкуренции; Промежуточный продукт — часть совокупного выпуска, приспособленная производителем промежуточного продукта для инвестиционного потребления, единственные его издержки связаны с приобретением конечного продукта по единичной цене. Монопольным правом на производство промежуточного продукта обладает его производитель; это право он получает, покупая патент на производство продукта у научно-исследовательского сектора. Патент — это монопольное право на использование определенной технологии, произведенной научно-исследовательским сектором и проданное производителю промежуточной продукции; Патент является активом, и его доходность выравнивается с процентной ставкой; Цена патента выражается как сумма потока будущей дисконтированной прибыли, которую он принесет монопольному владельцу; При совершенной конкуренции в научно-исследовательском секторе цена патента равна предельным издержкам инноватора: q = w/bN = const = η Производственная функция научно-исследовательского сектора вводится в модель в зависимости от объема труда в секторе и имеющегося объема разработок, которые используются для аналоговых новых технологий (зависимость от накопления физического капитала рассматривается как незначительная, физический капитал научно-исследовательского сектора включен в константу производительности): YN = bL R&D N, где b — параметр производительности в секторе R&D, константа; L — объем труда в секторе R&D; N — внешний эффект от имеющегося количества типов промежуточных продуктов (технологий). Устойчивый темп прироста основных переменных модели равен постоянной величине (монопольная прибыль и цена патента — постоянны): gC =gY = gK = const существует эндогенный рост с постоянным темпом, достигаемый за счет технического прогресса —производства инноваций в научно-исследовательском секторе Равновесный устойчивый рост зависит от соотношения отдачи актива модели — патента, приносящего монопольную прибыль, и субъективной дисконтной ставки. При превышении отдачи патента рост будет положительным и эндогенным, так как зависит от поведенческого параметра. отдача патента, а следовательно, и устойчивый равновесный рост, зависит от доли монопольной прибыли в общем объеме выпуска: чем выше доля монопольной прибыли, тем больше экономический рост. В модели эта взаимосвязь достигается за счет того, что монопольная прибыль полностью поступает на финансирование научно-технического прогресса; отдача патента зависит также от коэффициента производительности научно-исследовательского сектора; отдача соотносится с объемом труда в конечном секторе. Оптимальный с точки зрения благосостояния всего общества рост можно получить путем максимизации полезности социальным планером, действующим в интересах общества в целом (государством), по отношению к заданным ограничениям инвестиций в физический капитал, ограничению сектора технического прогресса и ограничению распределения труда; В результате математических преобразований величина темпа экономического роста, оптимальная с точки зрения общества, больше, чем ранее выведенное выражение для равновесного устойчивого экономического роста; ВЫВОД: государство может поддерживать научно-исследовательский сектор, повышая его отдачу и способствуя тем самым экономическому росту, приближая его к оптимальному. Существует возможность постоянного устойчивого роста на основе эндогенного научно-технического прогресса, производство которого рассматривается как результат целенаправленной человеческой деятельности, как отдельный сектор экономики — научно-исследовательский сектор, продуктом которого являются патенты на созданные инновации |
