Л-4 Матрицы. Лекция 4 Раздел Матрицы. Первоначальные сведения о матрице
 Скачать 335 Kb. Скачать 335 Kb.
|
|
Лекция 4 Раздел 3. Матрицы. 3.1. Первоначальные сведения о матрице. Определение 1. Прямоугольной,или 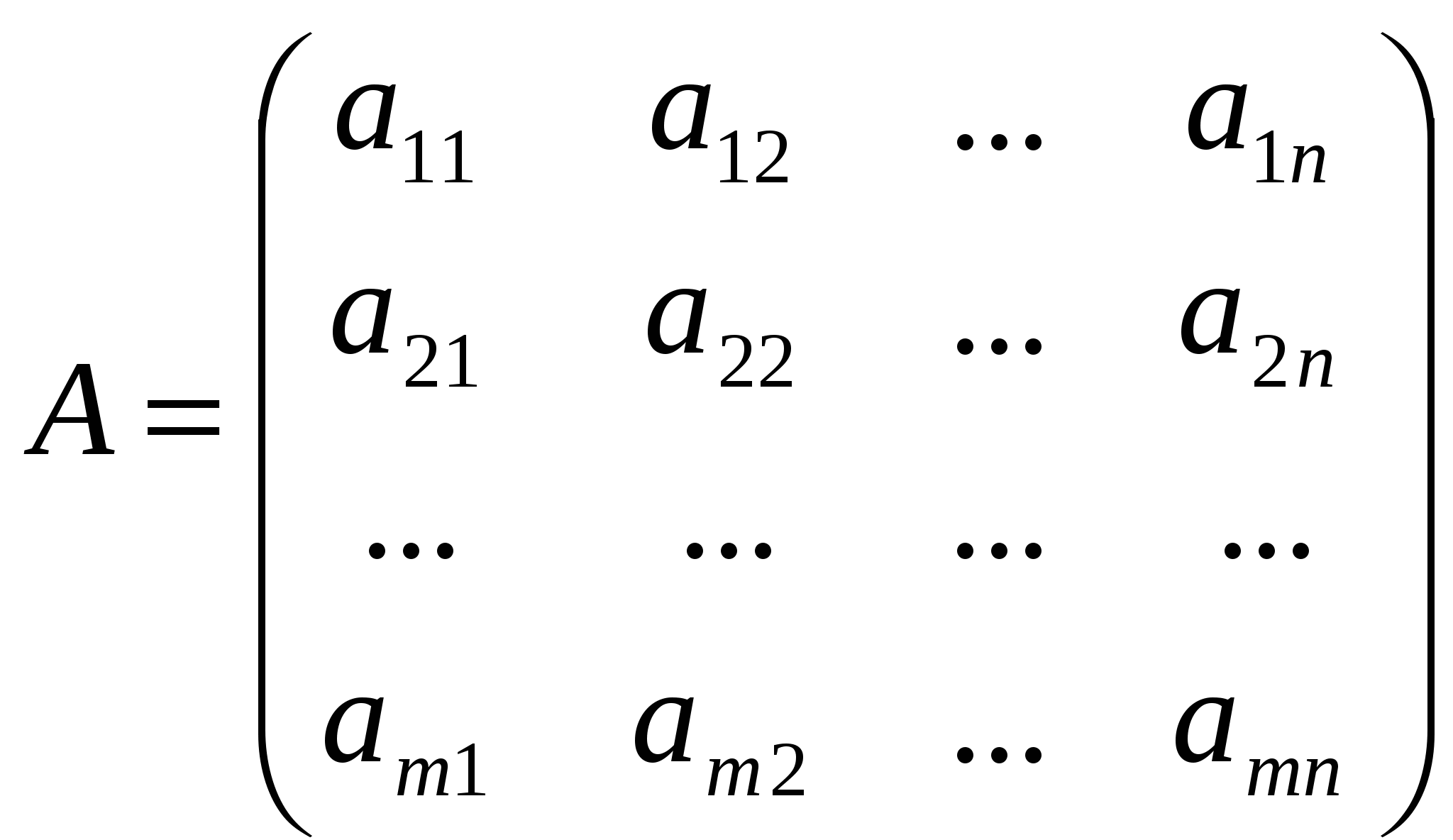 . (1) . (1)Размер матрицы А обозначается символом: Например, матрица 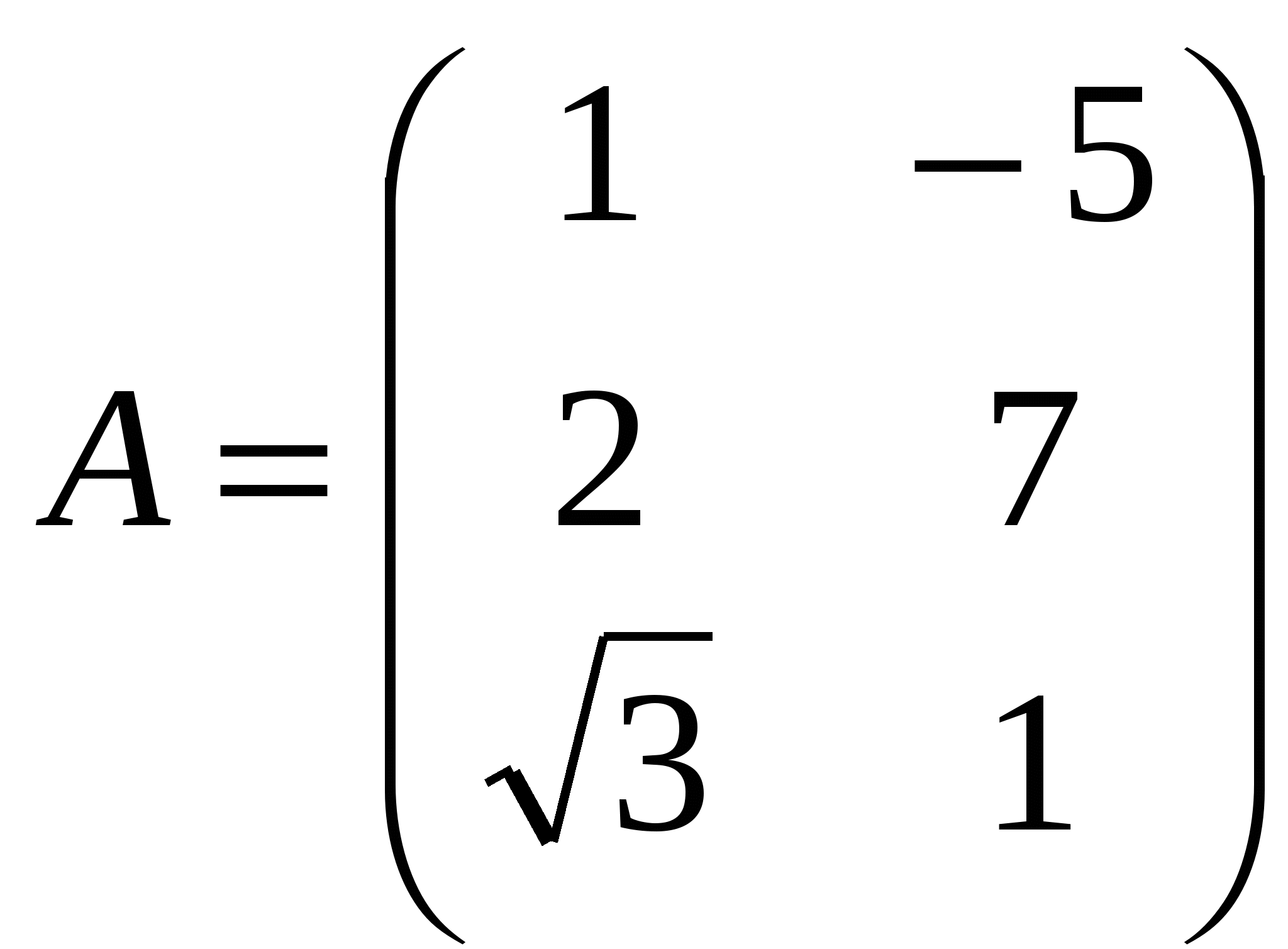 имеет размер Определение 2. Матрица называется комплексной, если хотя бы один ее элемент является комплексным числом, и действительной, если все ее элементы – действительные числа. Пример. 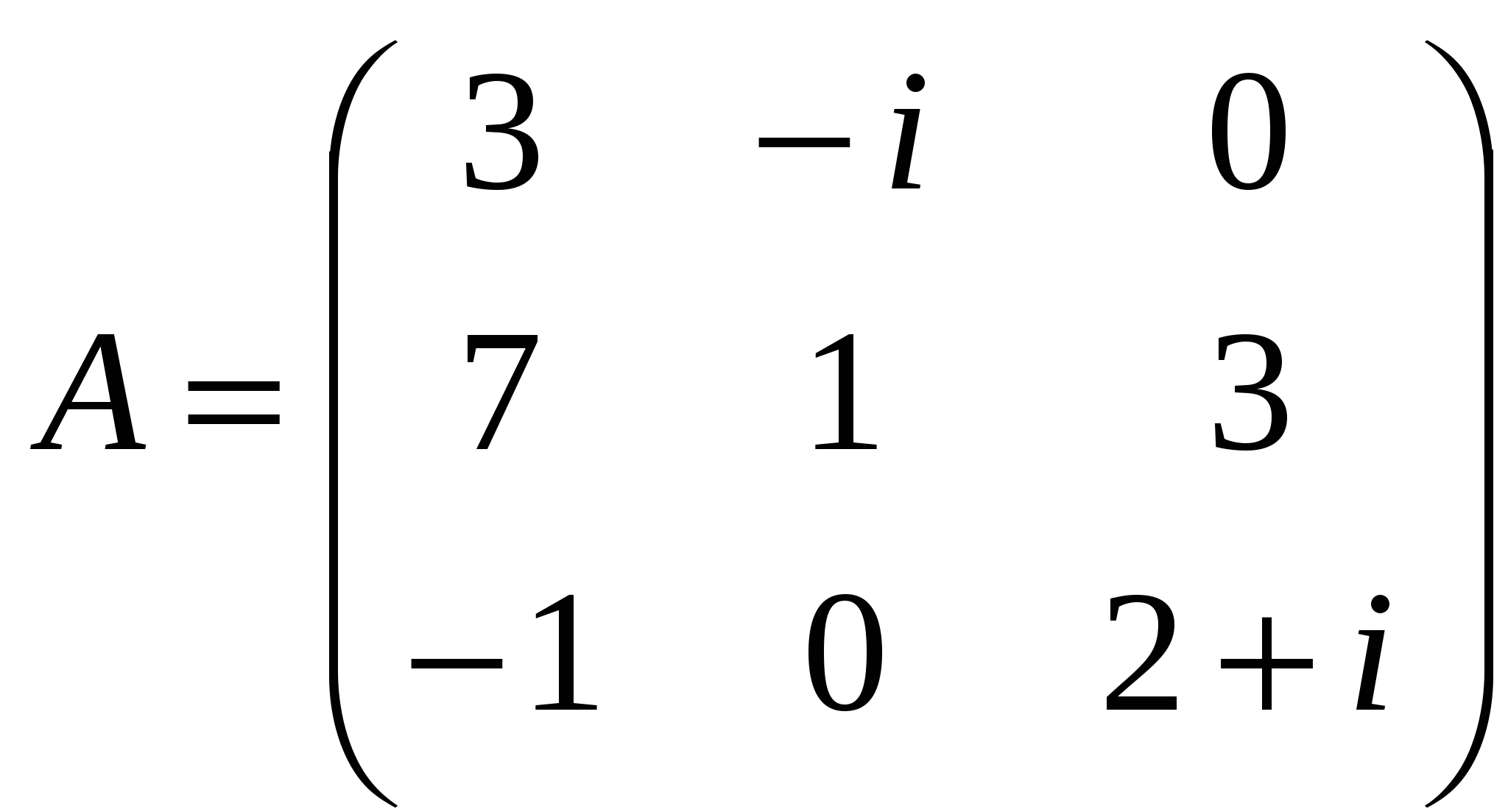 - комплексная матрица, - комплексная матрица, 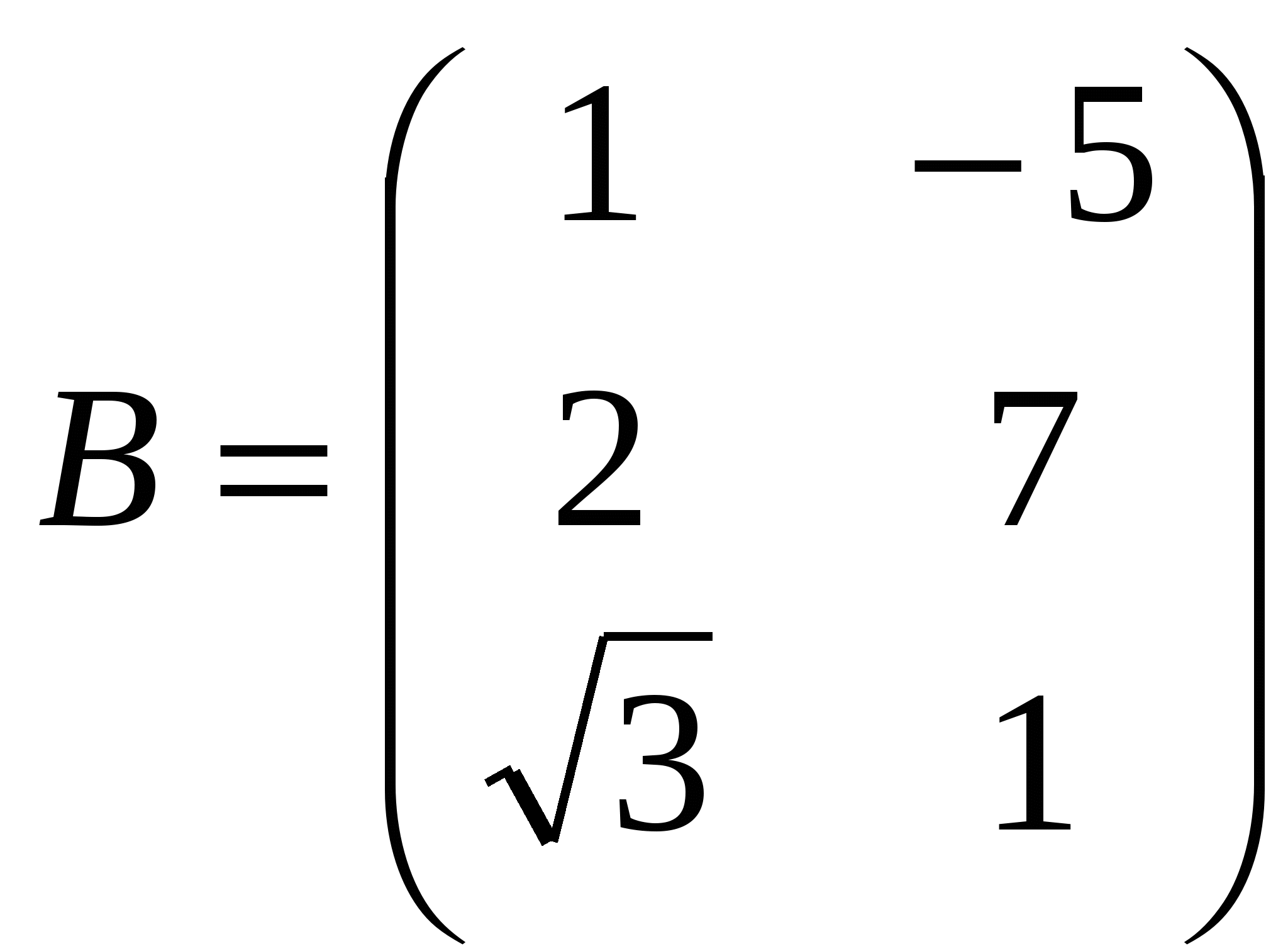 - действительная матрица. - действительная матрица.В учебной и математической литературе встречаются следующие обозначения матриц: Матрицы А и В имеют одинаковый размер, т.е. Определение 3. Матрицы А и В называются равными, если Матрица, состоящая из одной строки, называется матрицей-строкой: Матрица, имеющая лишь один столбец, называется матрицей-столбцом: 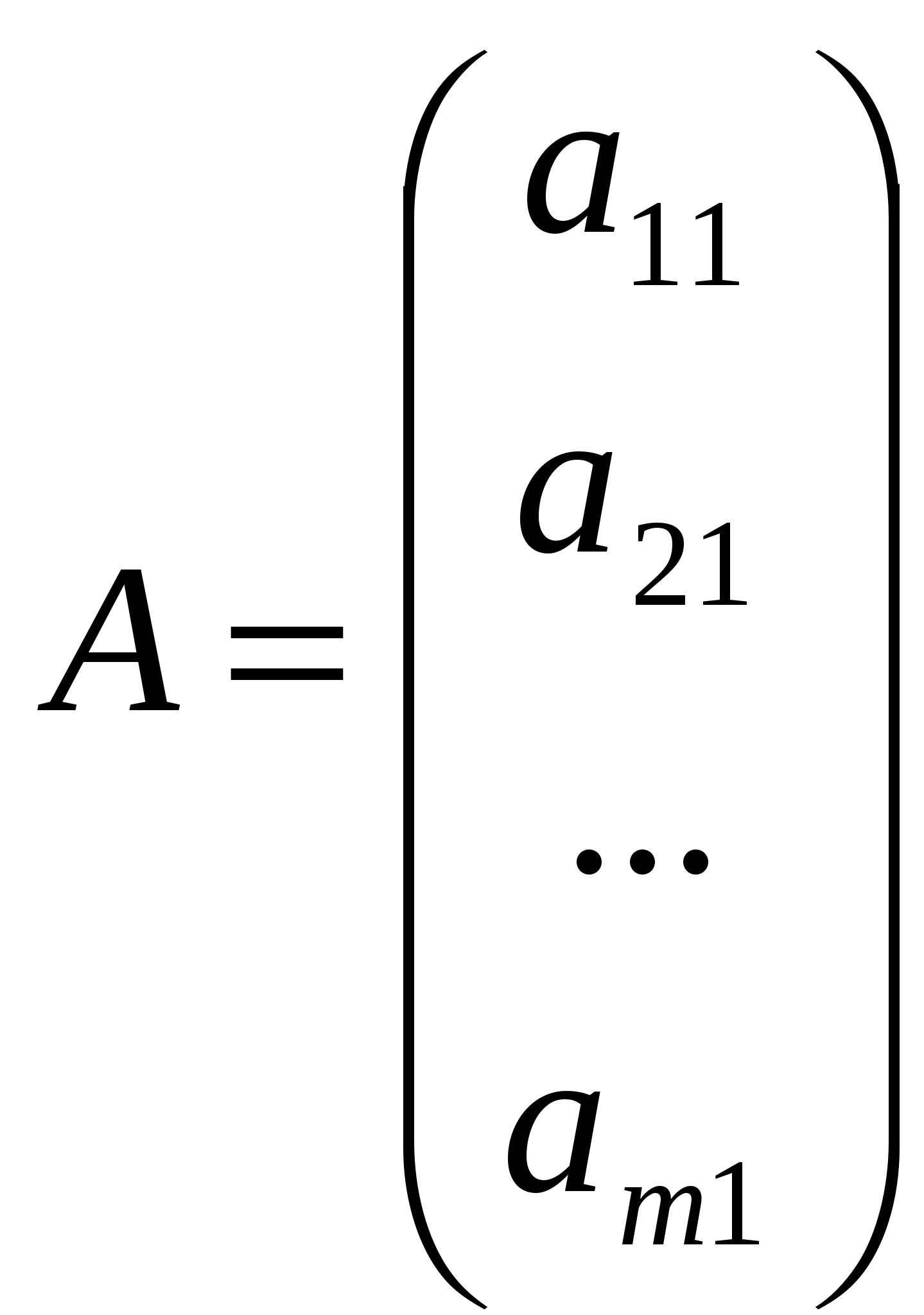 , , Матрица, состоящая из нулей, называется нулевой. Нулевые матрицы разных размеров принято обозначать одним и тем же символом О, что не приводит к недоразумениям. 3.2 Линейные действия над матрицами. Определение 1. Пусть матрицы А, В и С такие, что Пример. а) б) Определение 2. Матрица Пример. Если Свойства операции сложения матриц. Для матриц А, В, С, О таких, что 1. 2. 3. 4. Сложение матриц обладает обратной операцией – вычитанием. Определение 3. Пусть матрицы А, В и С такие, что Пример. а) б) Определение 4. Пусть матрицы А и В такие, что Пример. Свойства операции умножения матрицы на число. Для матриц А и В таких, что 1. 2. 3. 4. 3.3 Умножение матриц. Определение 1. Матрица А называется согласованнойс матрицей В, если число столбцов матрицы А равно числу строк матрицы В, т.е. Из согласованности матрицы А с матрицей В, не следует согласованность матрицы В с матрицей А. Пример. 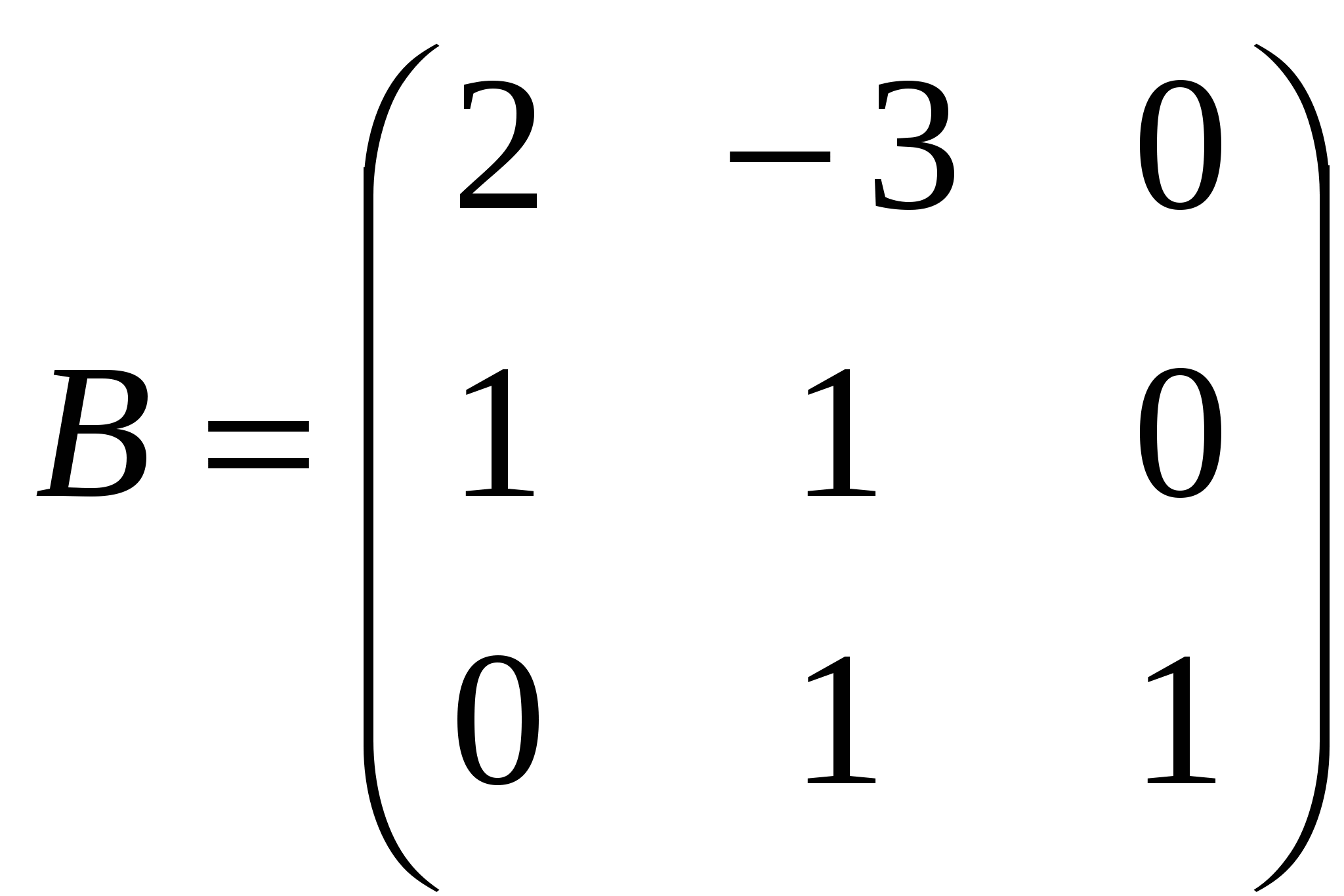 . . Матрица А согласована с матрицей В (А имеет 3 столбца, В – 3 строки), но матрица В не согласована с матрицей А (В имеет 3 столбца, А – 3 строки). Определение 2. Пусть матрица А согласована с матрицей В, т.е. Пример. 1) 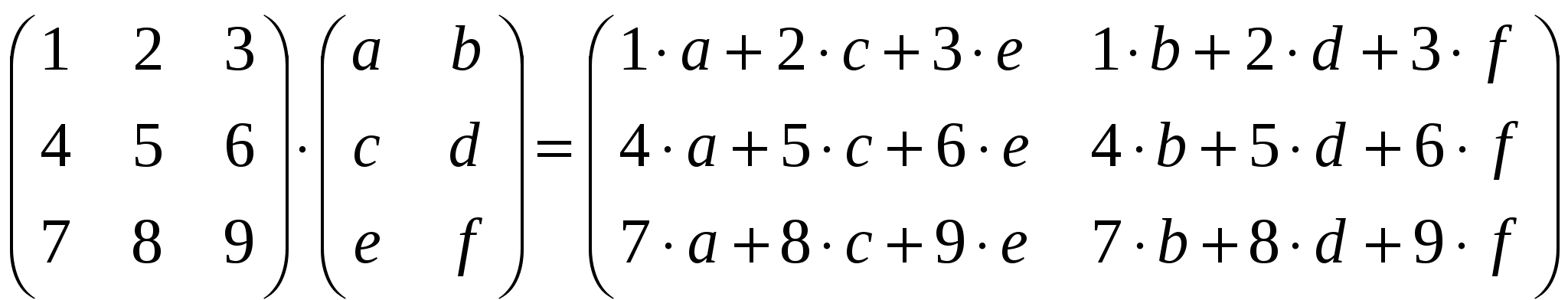 , , Оба произведения Пример. Для матриц 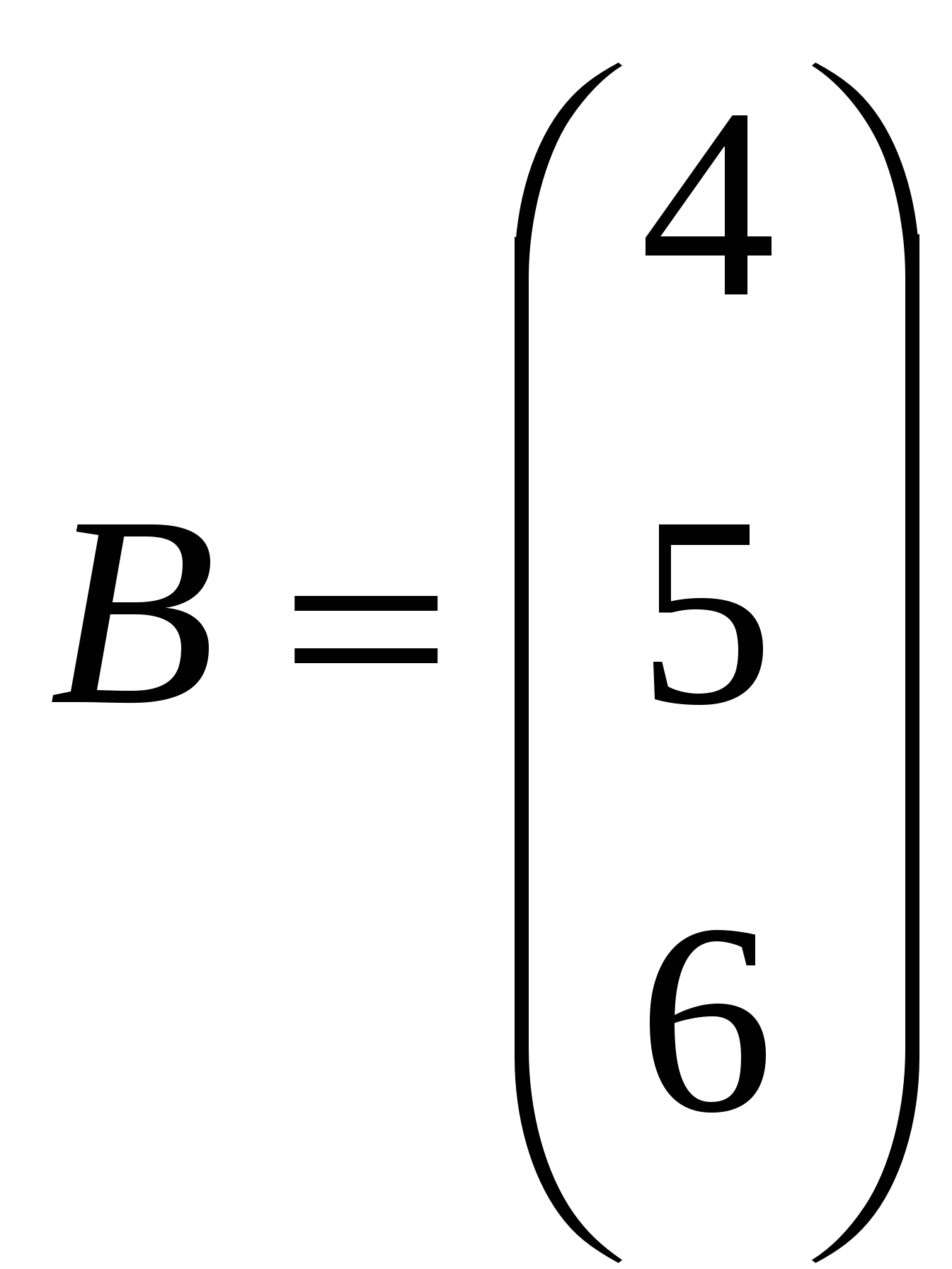 определены произведения определены произведения 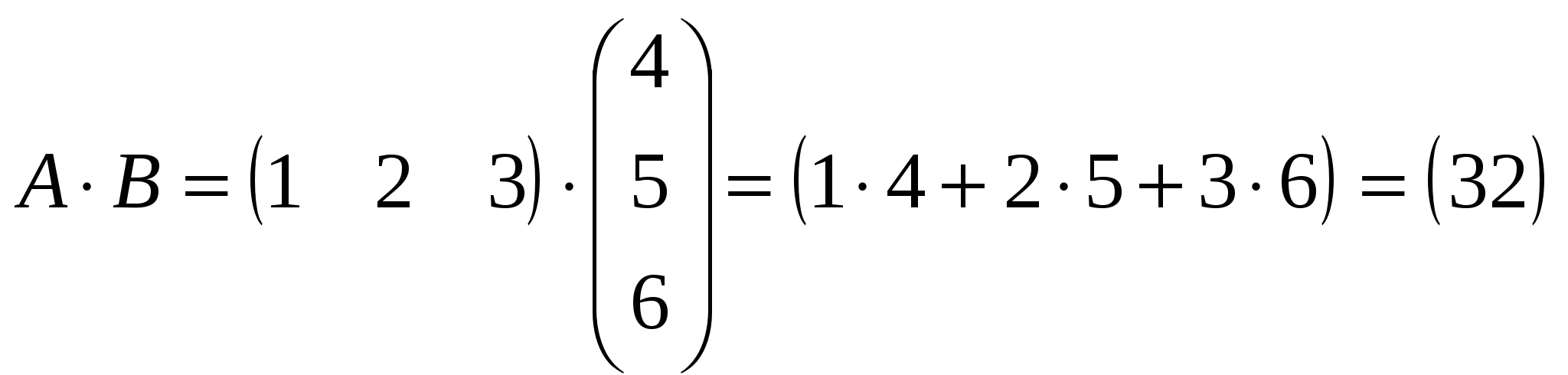 , , Вычислим 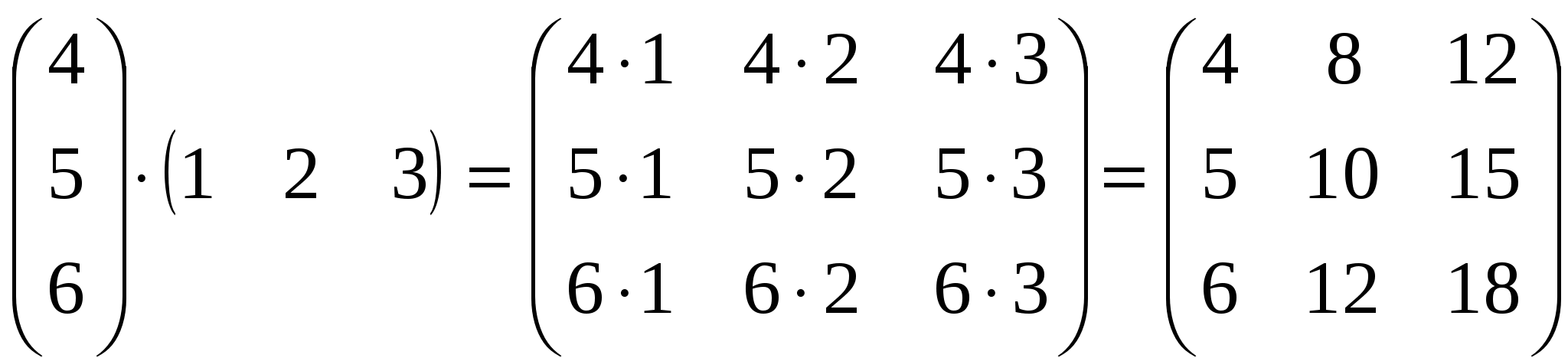 , , Из приведенных примеров видно, что если даже оба произведения Свойства операции умножения матриц. 1. 2. 3. Эти свойства доказываются непосредственной проверкой. Докажем, например, свойство 3. Пусть 3.4 Операции над матрицами: транспонирование, комплексное сопряжение, сопряжение по Эрмиту. Определение 1. Транспонированием матрицы А называется операция замены каждой ее строки столбцом с тем же номером. Полученную в результате этой операции матрицу называют транспонированной к матрице А и обозначают через Если А – матрица размера Пример. Запишем транспонированную матрицу: 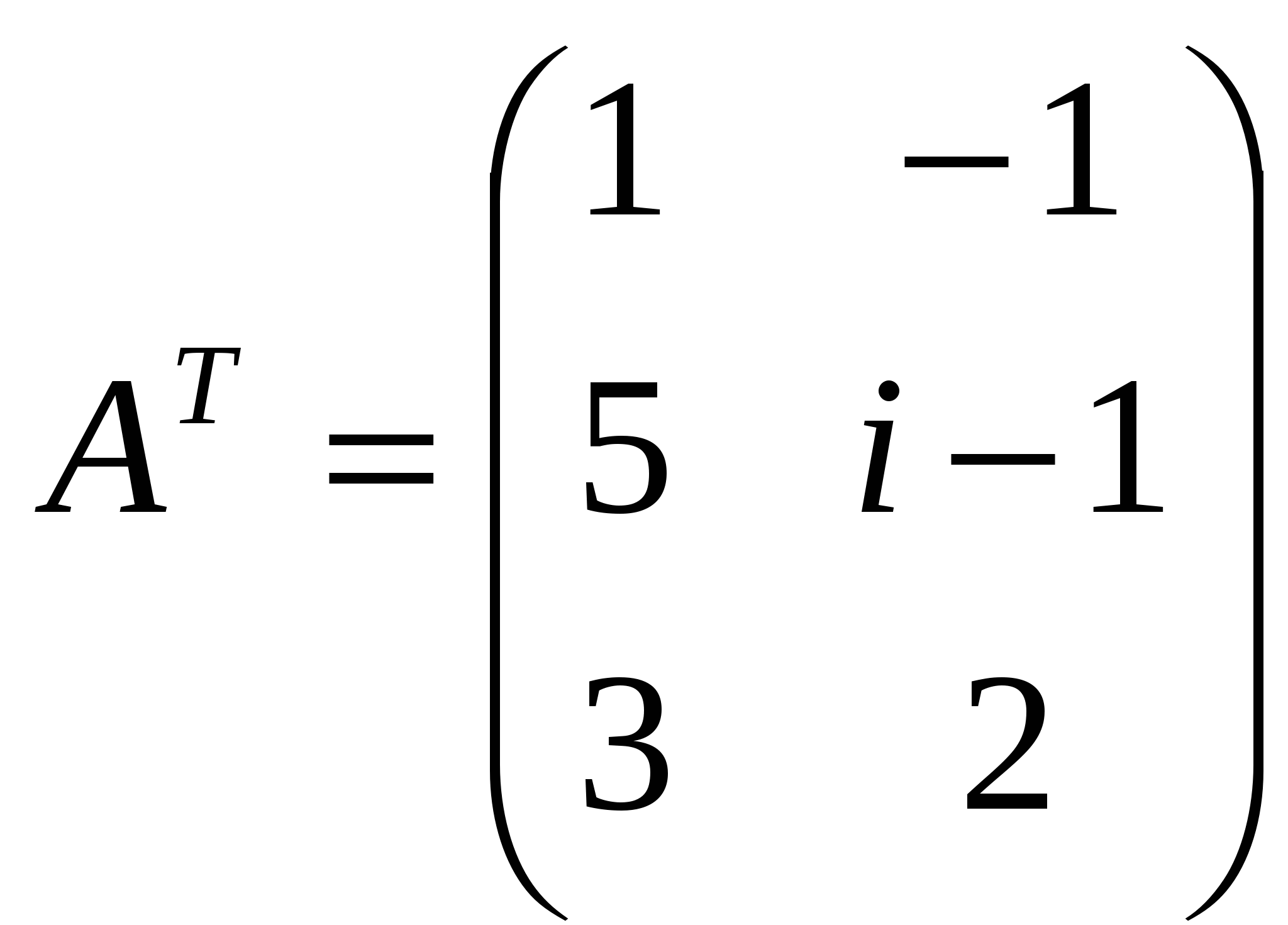 , , Определение 2. Комплексным сопряжением матрицы А называется операция замены каждого элемента матрицы А на комплексно сопряженный ему элемент. Матрица, полученная в результате этой операции, называется комплексно сопряженной с матрицей А и обозначается Пример. Пусть Представим все элементы матрицы А в алгебраической форме тогда комплексно сопряженная матрица имеет вид Определение 3. Сопряженим по Эрмитуматрицы А называется операция сочетающая транспонирование и комплексное сопряжение. Матрица, полученная в результате этой операции, называется эрмитово-сопряженной с матрицей А и обозначается Пример. Пусть тогда 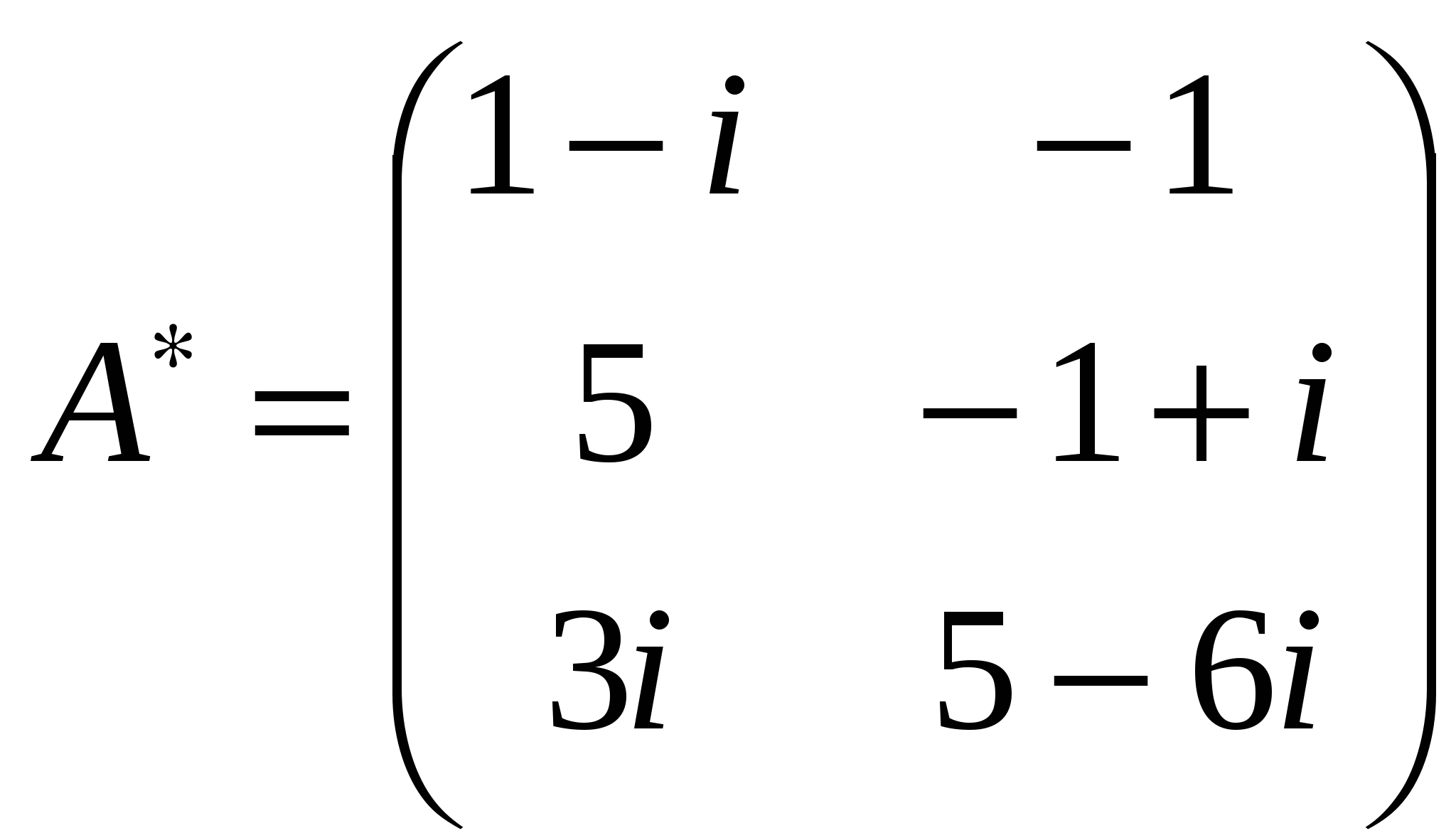 . .Для всех трех операций, непосредственной проверкой, можно доказать следующие свойства: I. II. 1) 2) 3) III. IV. 7) 8) 9) 3.5 Квадратные матрицы. Определение 1. Квадратной матрицей называется матрица А, у которой число строк равно числу столбцов, т.е. В квадратной матрице совокупность элементов на линии, соединяющей верхний левый угол с правым нижним, называют главной диагональю. У элементов главной диагонали номер строки совпадает с номером столбца. Например, у матрицы размера Определение 2. Квадратные матрицы, у которых отличны от нуля лишь элементы главной диагонали, т.е. 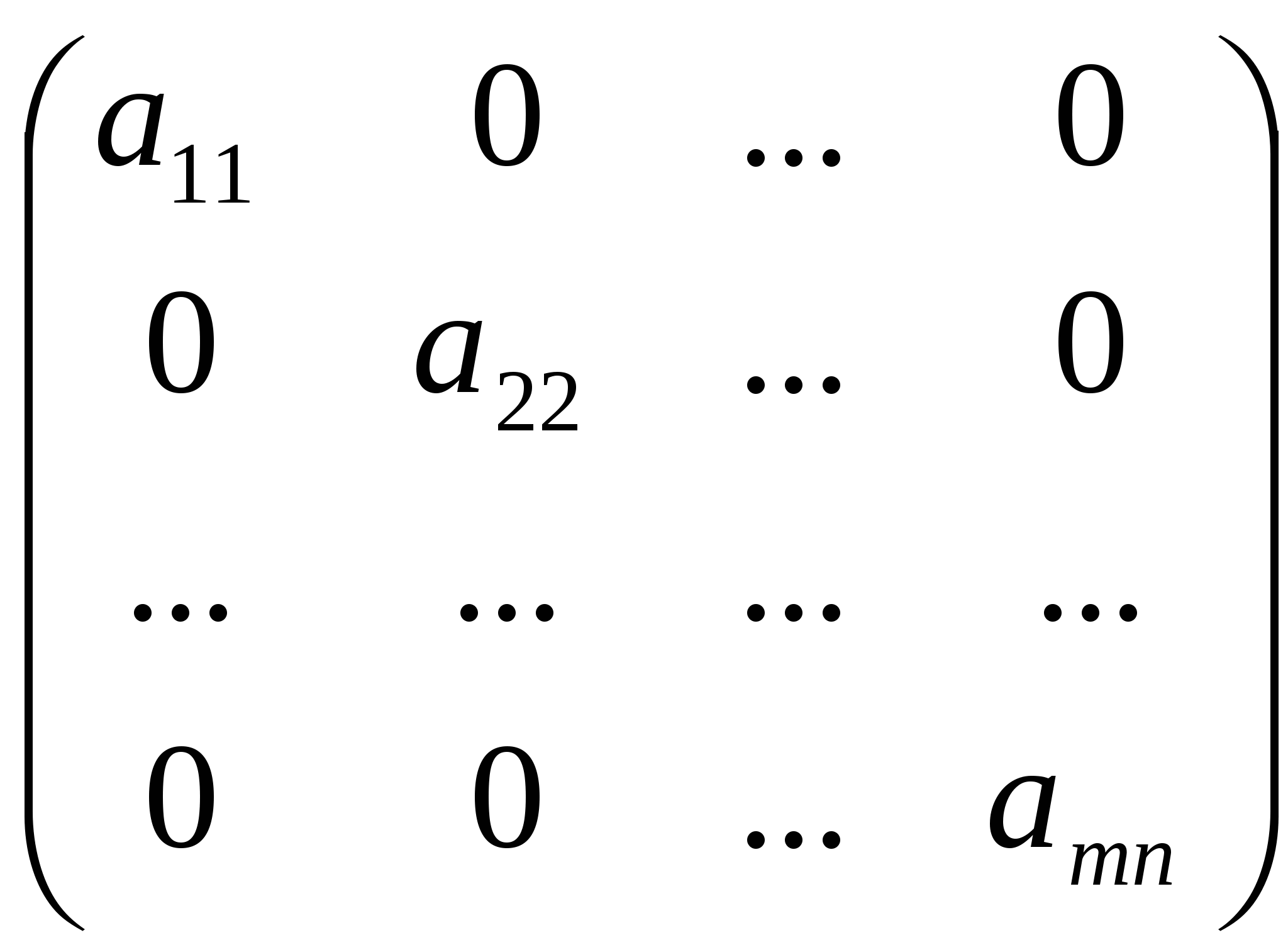 называют диагональными. Диагональная матрица, у которой все элементы главной диагонали одинаковые, называется скалярной. Частным случаем скалярных матриц является единичная матрица 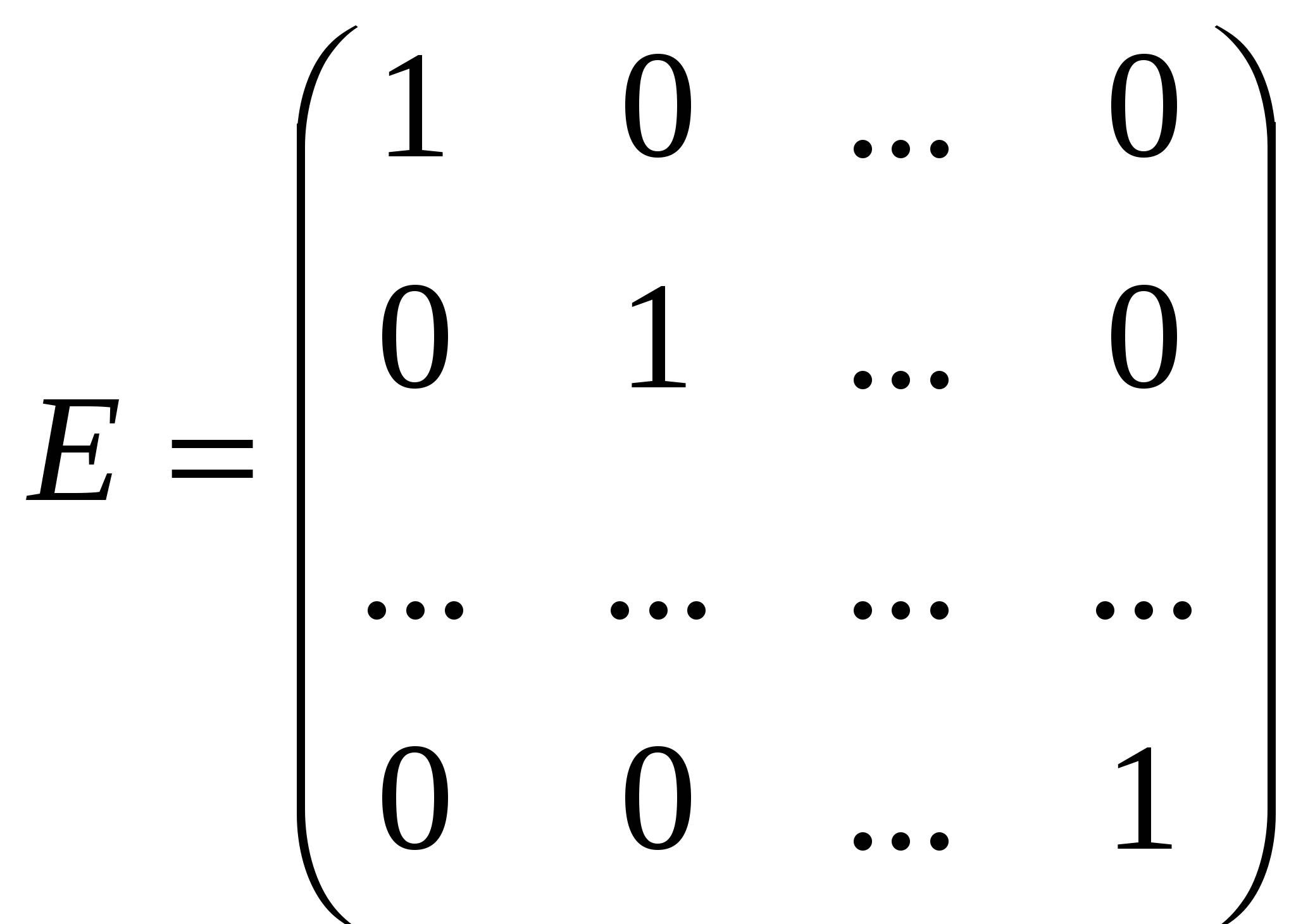 . .Легко видеть, что Определение 3. Квадратную матрицу называют треугольной, если все ее элементы, стоящие выше (или ниже) главной диагонали, равны нулю. При этом матрицу вида 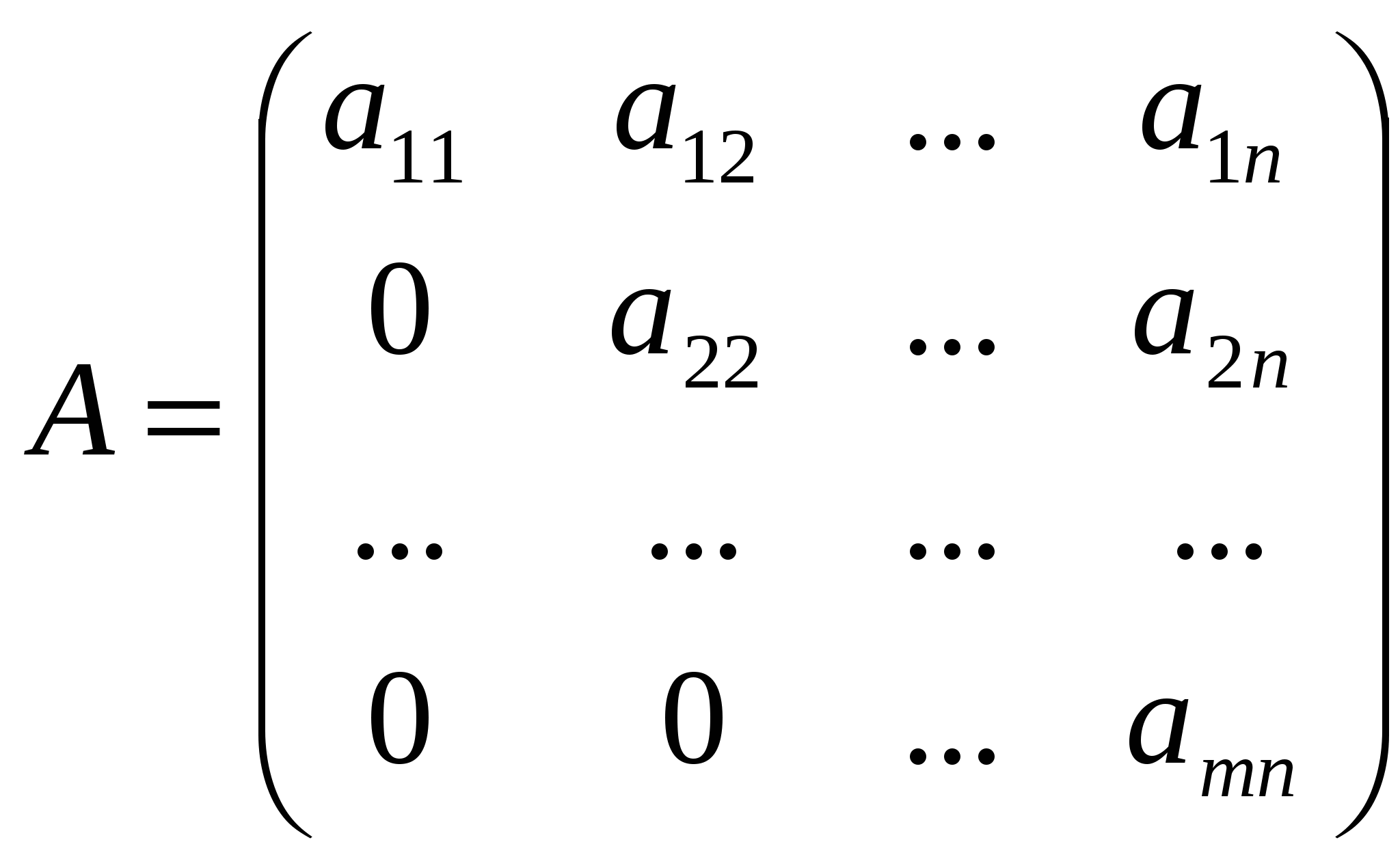 называют верхней треугольной матрицей, а матрицу вида 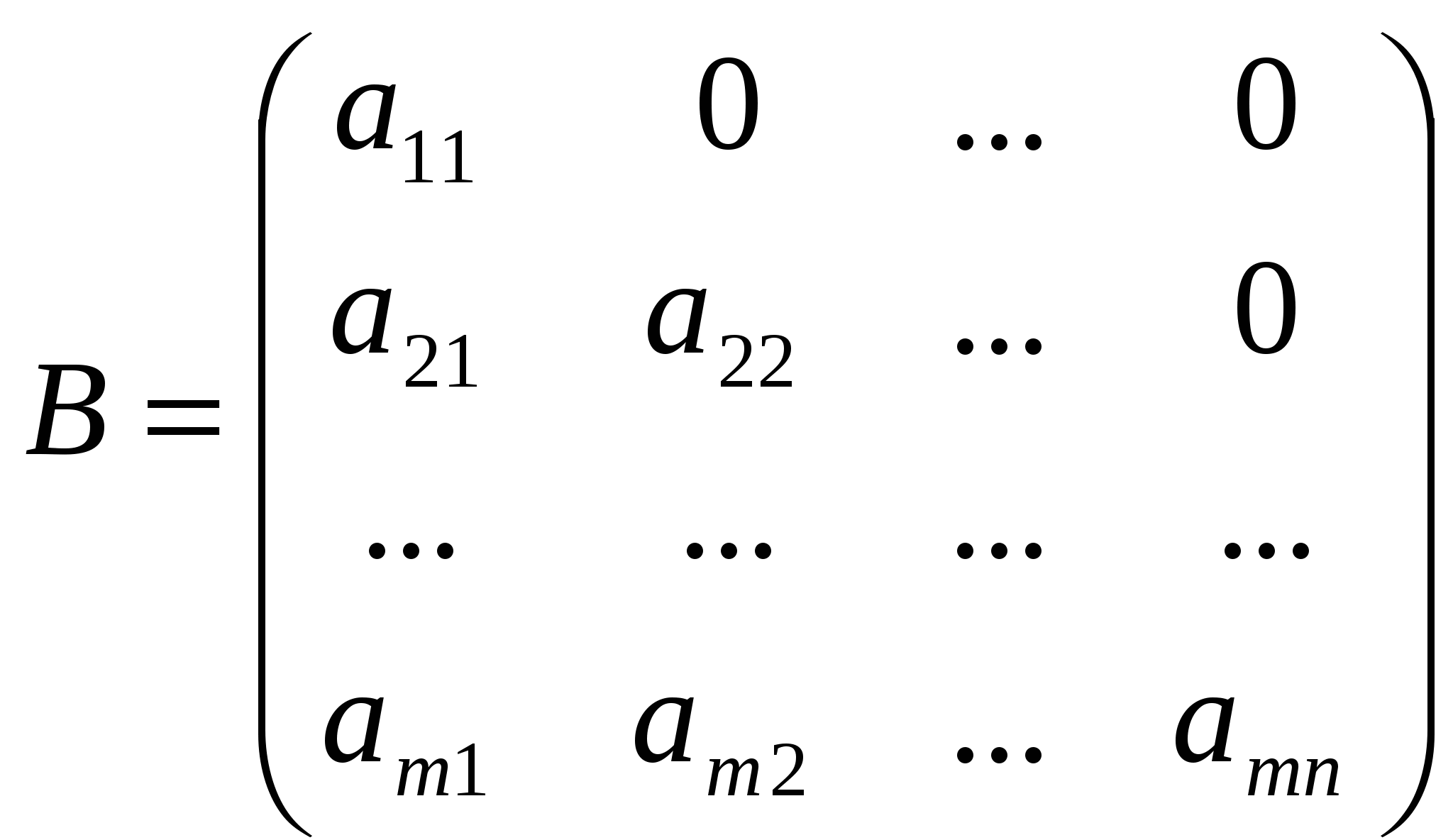 -нижней треугольной матрицей. Определение 4. Квадратную матрицу А называют симметрической, если она не меняется при транспонировании, т.е. Например, рассмотрим матрицу 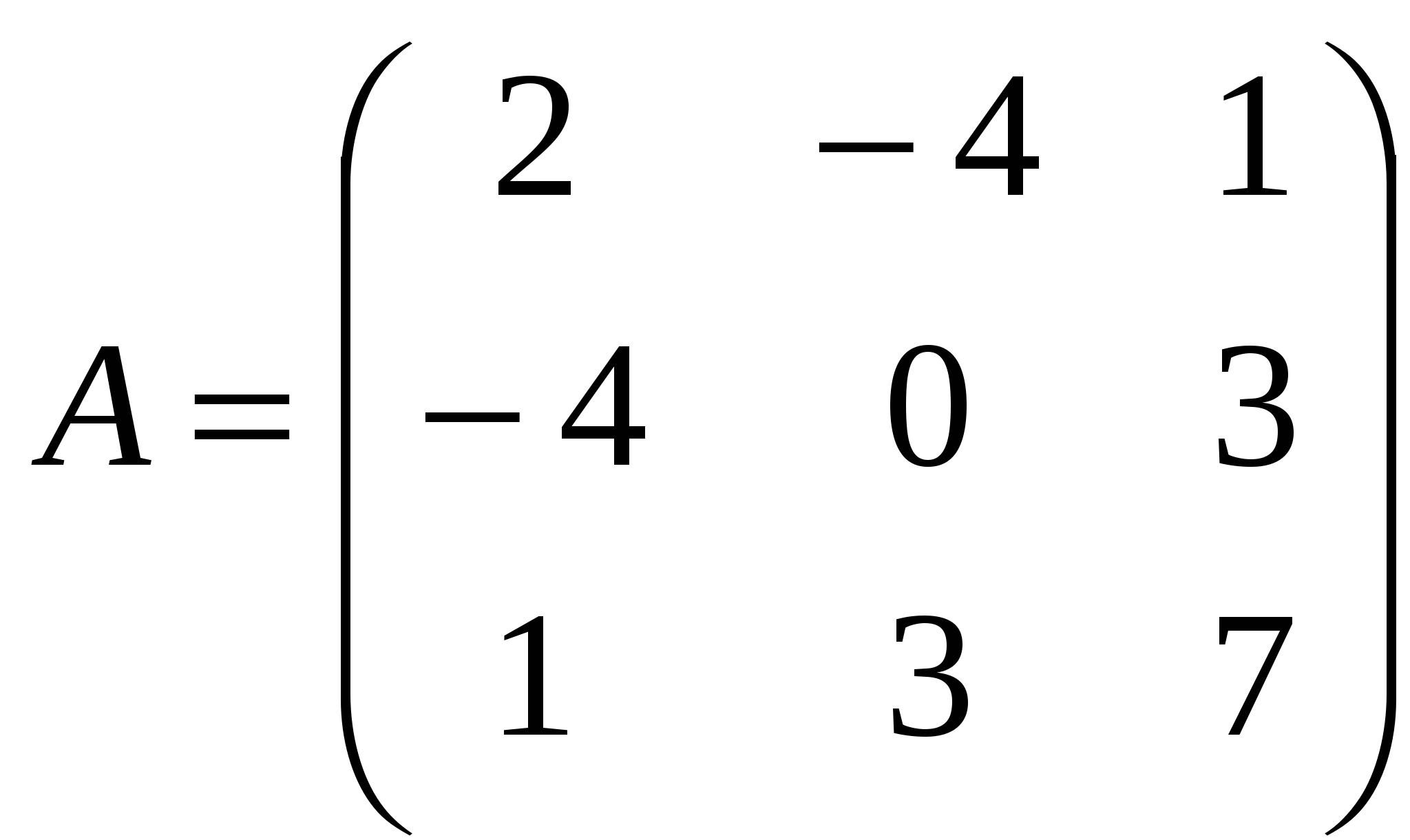 . Так как транспонированная матрица имеет вид: . Так как транспонированная матрица имеет вид: 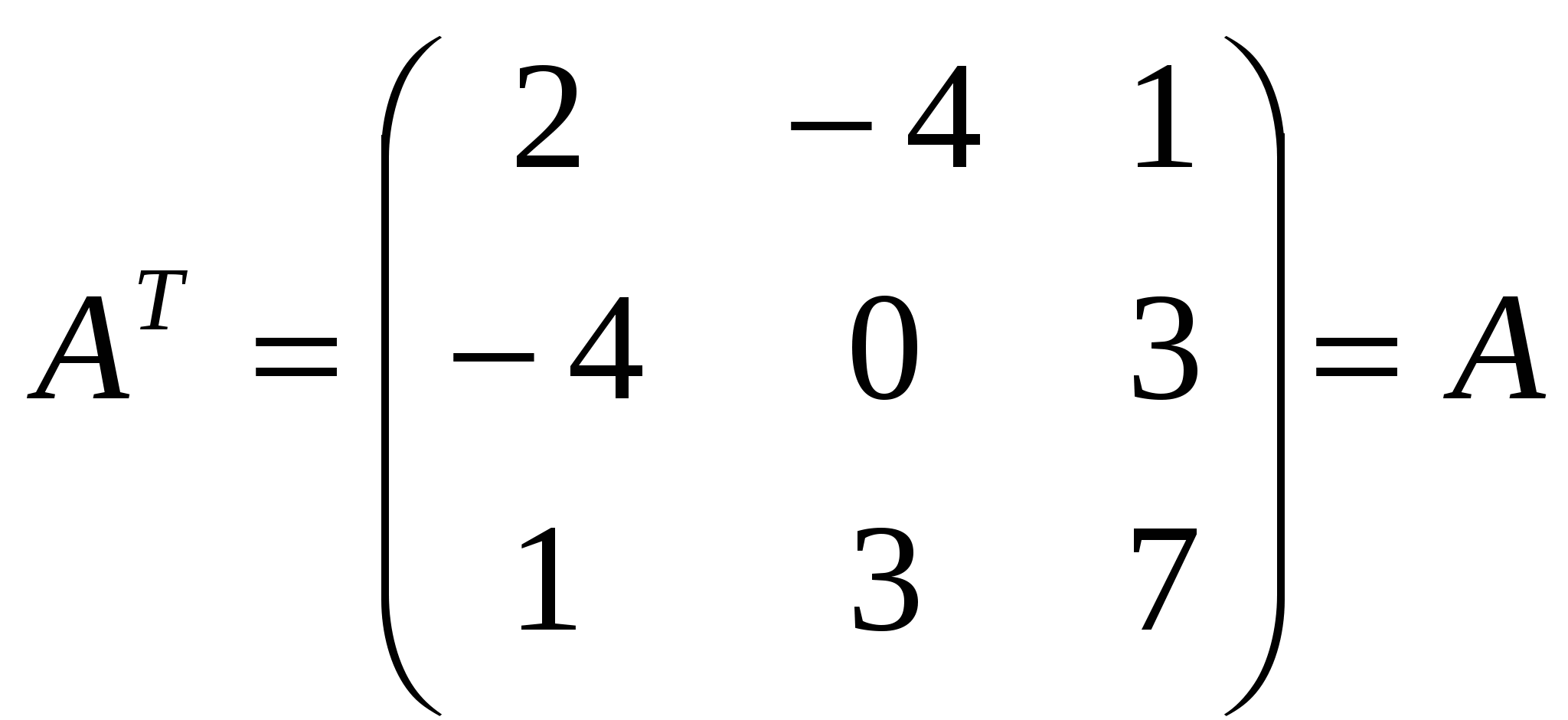 , то матрица А симметрическая. , то матрица А симметрическая.Определение 5. Квадратная матрица А называется кососимметрической, если при транспонировании она меняет свой знак, т.е. Например, для матрицы 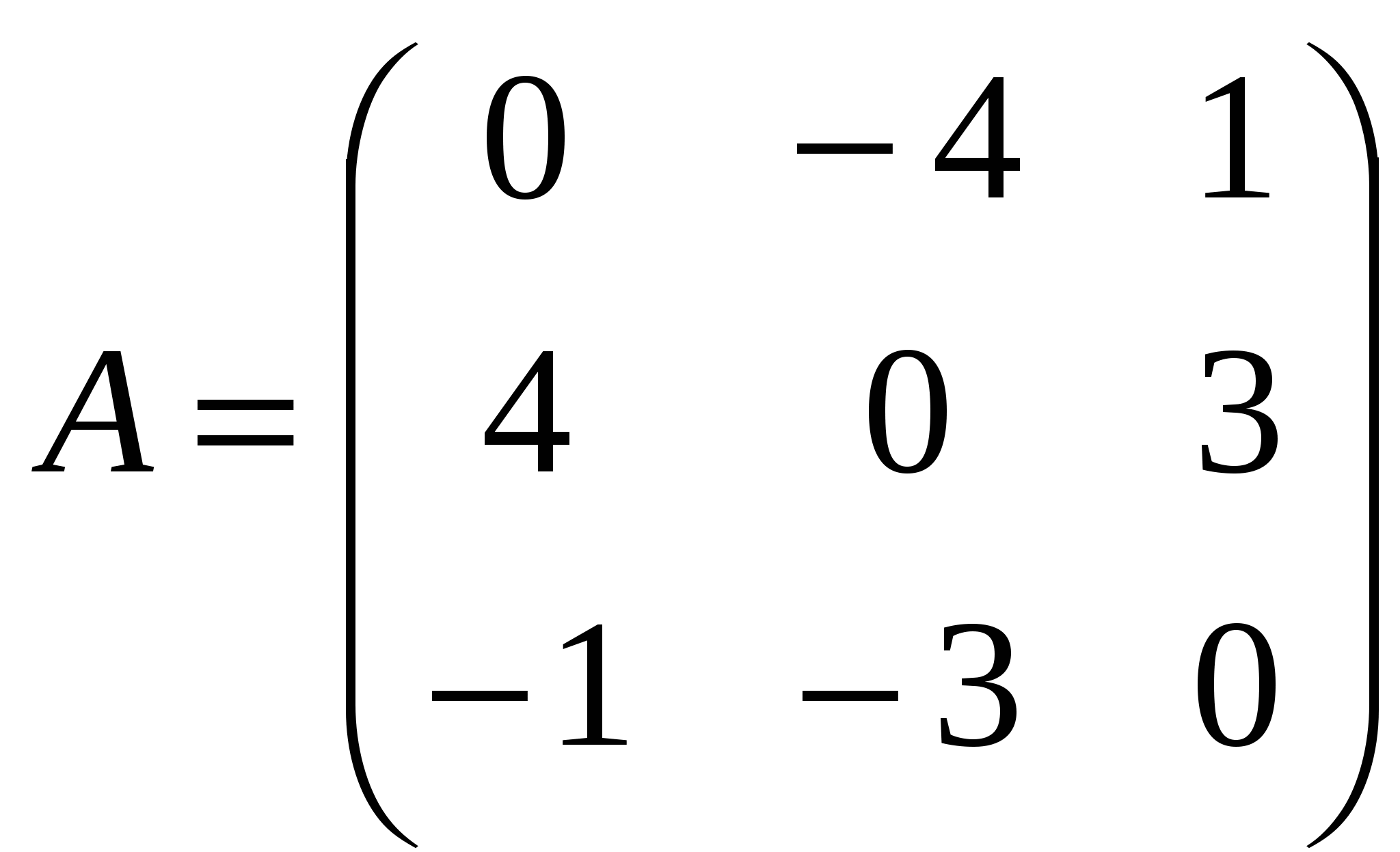 , транспонированная матрица имеет вид: , транспонированная матрица имеет вид: 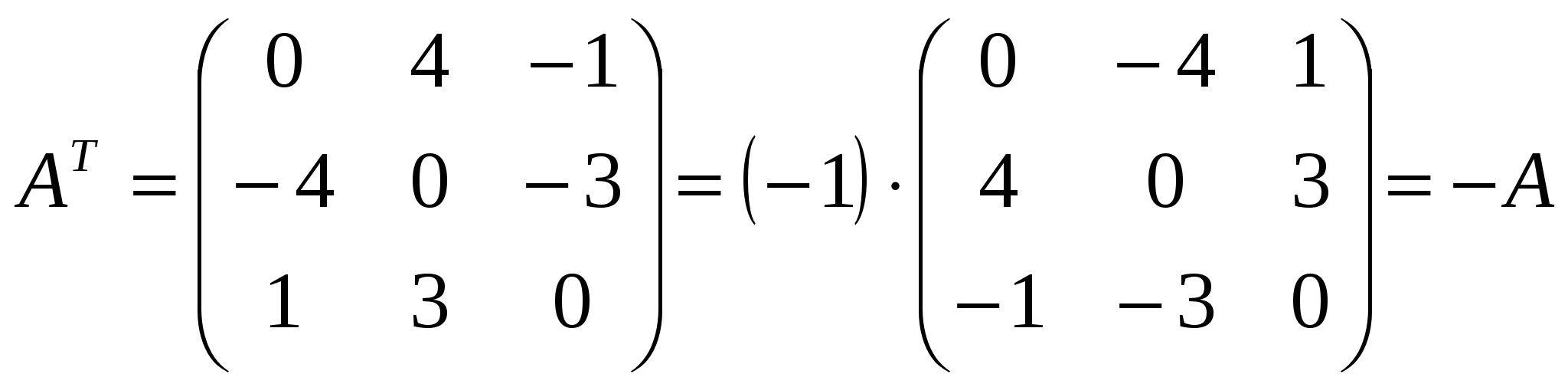 , поэтому матрица А кососимметрическая. , поэтому матрица А кососимметрическая.Определение 5. Квадратная матрица называется эрмитовой, если она равна эрмитово-сопряженной, т.е. Определение 6. Квадратная матрица называется ортогональной, если ее произведение на транспонированную матрицу равно единичной матрице, т.е. Определение 7. Квадратная матрица называется унитарной, если ее произведение на эрмитово-сопряженную матрицу равно единичной матрице, т.е. При помощи матриц изучаются свойства различных устройств в электротехнике и технике сверхвысоких частот (СВЧ). В частности, в технике сверхвысоких частот (СВЧ) применяют матрицу рассеяния S, связывающую амплитуды волн, бегущих к устройству 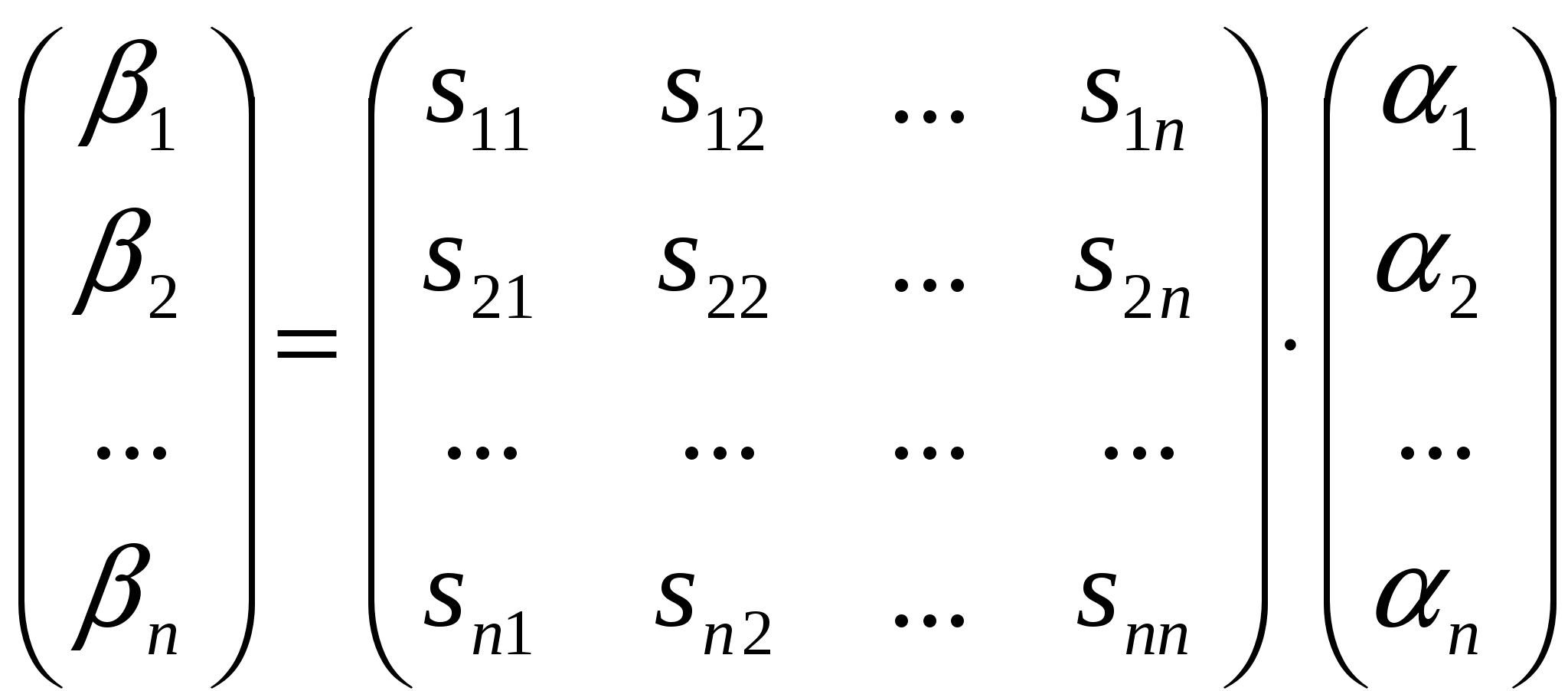 , ,где п – число каналов, по которым волны бегут к устройству или от него. В теории устройств СВЧ доказывается, что необходимым и достаточным условием отсутствия потерь в устройстве служит унитарность матрицы рассеяния. Пример. Проверить, обладает ли потерями устройство, описываемое матрицей рассеяния 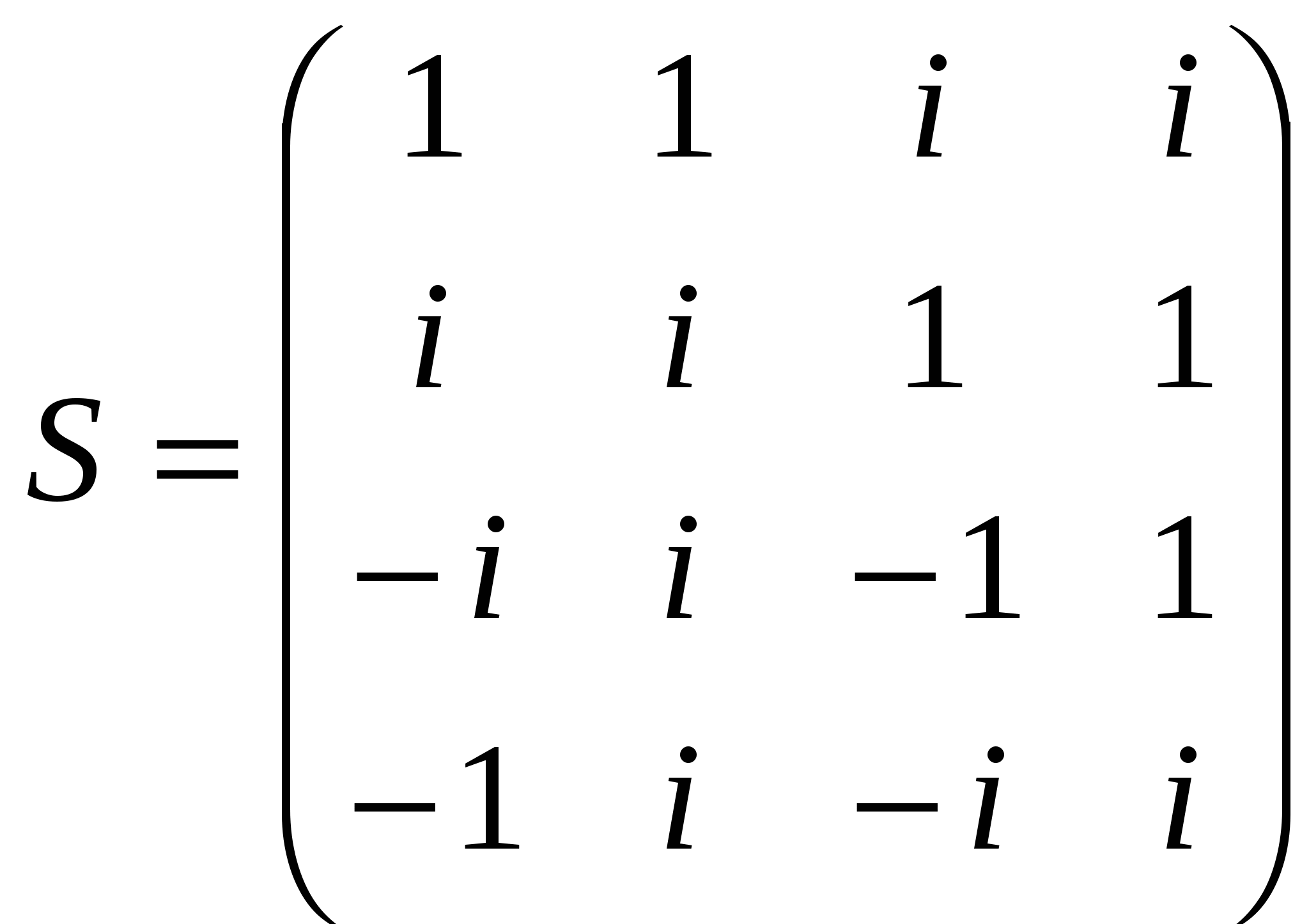 . .Решение. Проверим, будет ли матрица S унитарной. 1. Ищем эрмитово-сопряженную матрицу. 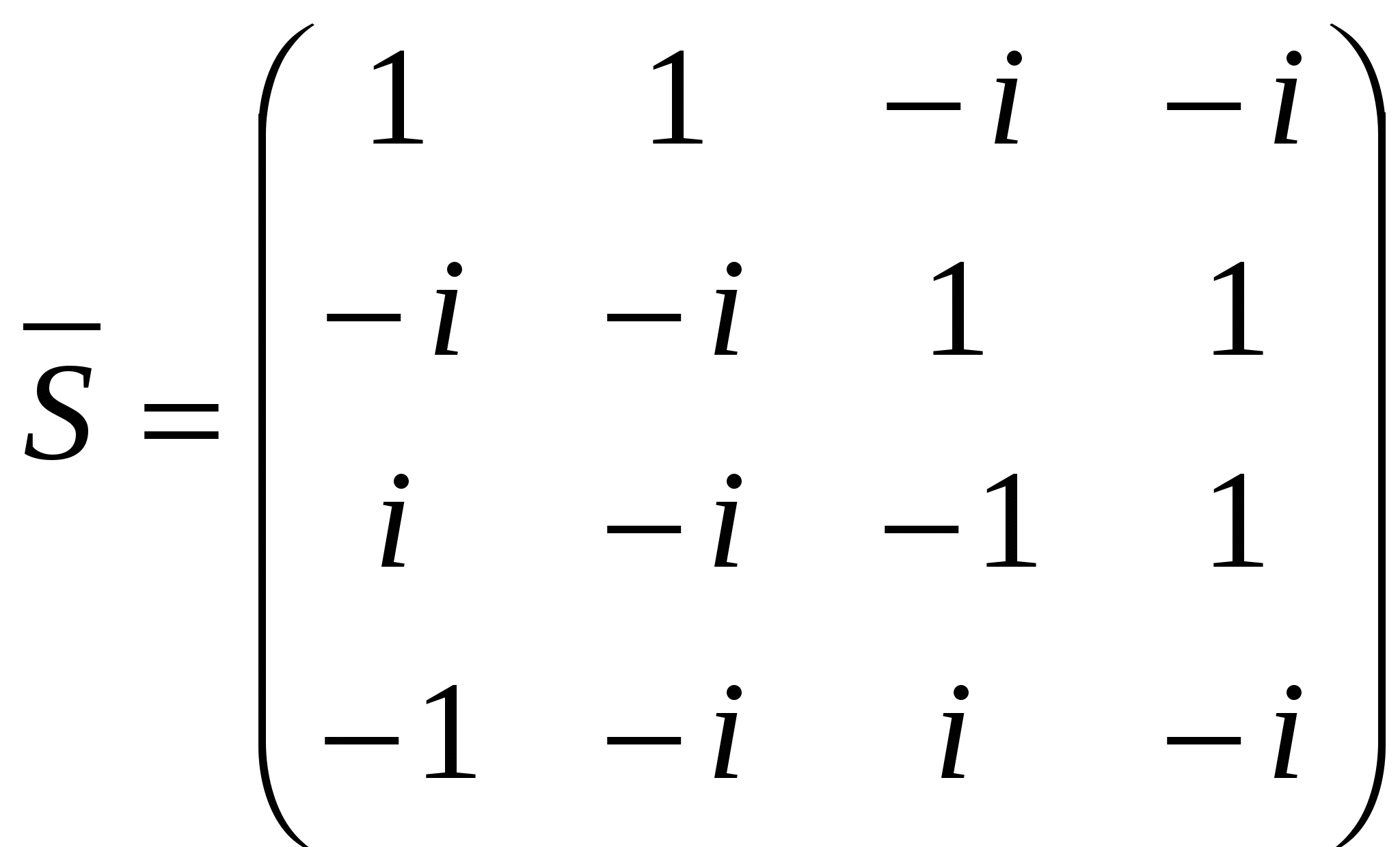 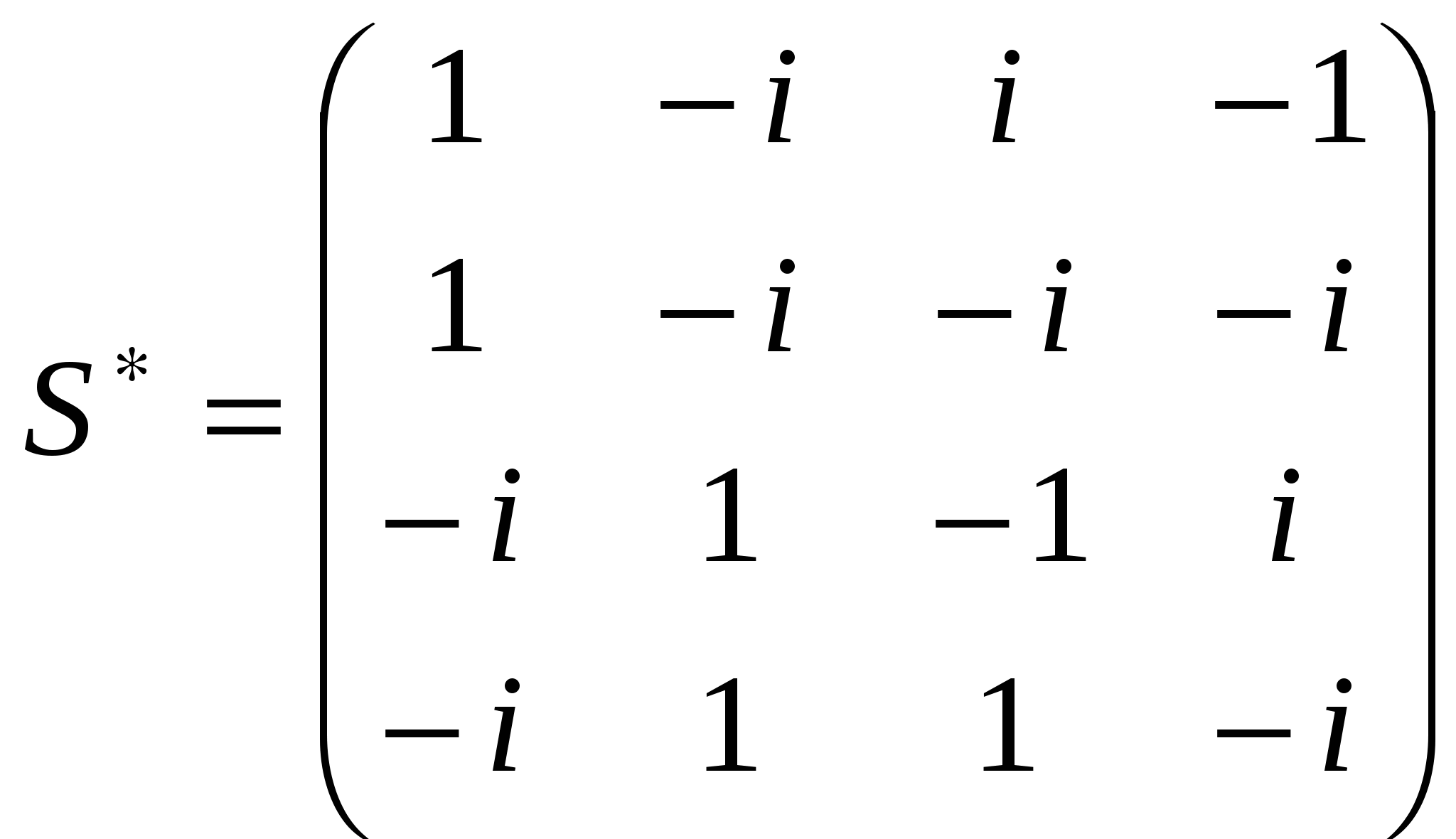 2. Проверяем равенство 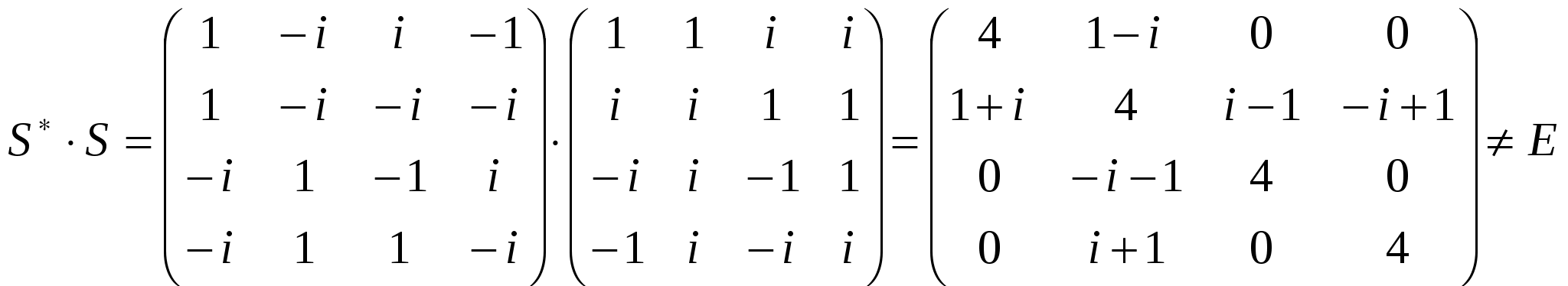 |
