Вероятность 5. Лекция 5 Последовательность независимых испытаний
 Скачать 256 Kb. Скачать 256 Kb.
|
ЛЕКЦИЯ 5Последовательность независимых испытаний. Формула Бернулли. Локальная и интегральная теоремы Муавра-Лапласа. Теорема Пуассона. 3.6. Формула БернуллиВ научной и практической деятельности постоянно приходится проводить многократно повторяющиеся опыты в сходных условиях. При этом, как правило, результаты предшествующих опытов никак не сказываются на результатах последующих опытов. Очень важен простейший тип таких опытов, когда в каждом из испытаний некоторое событие А может появляться с одной и той же вероятностью p и эта вероятность остается одной и той же, независимо от результатов предшествующих или последующих испытаний. Этот тип испытаний называется схемой повторных независимых испытаний, или схемой Бернулли. Исследование таких последовательностей заслуживает особого внимания в силу их исключительного значения в теории вероятностей и ее приложений. Изучение многих проблем в производстве, экономике, социологии и других отраслях науки и техники требует организации длительных наблюдений и экспериментов, т.е. организации схемы повторных испытаний. Например, особое значение схема Бернулли имеет в теории контроля. Так, перед тем как ввести в массовое производство новый тип прибора проводят многочисленные его испытания на безотказность, долговечность, простоту наладки и т.п. как раз по схеме Бернулли. Поставим задачу в общем виде. Пусть в результате испытания возможны два исхода: либо появление события А (успех), либо не появление события (неуспех). Проведем n испытаний Бернулли, т.е. что все n испытаний независимы и вероятность появления события А в каждом отдельном взятом испытании постоянна и от испытания к испытанию не изменяется (т.е. испытания проводятся в одинаковых условиях). Обозначим вероятность P(A) появлений события А в отдельном испытании буквой p, т.е. P(A)=p, а вероятность противоположного события P() – буквой q, т.е. P() = 1–P(A) = 1–p = q. Найдем вероятность Pn(m) того, что событие A появится ровно m раз в n испытаниях Бернулли. Отметим, что здесь не требуется появления события А ровно m раз в строго определенной последовательности. Вероятность элементарного исхода, в котором событие А наступит ровно m раз, равна pmqn–m. Однако число таких элементарных исходов совпадает с числом способов, которыми можно выбрать m мест из имеющихся n, не учитывая порядка, т.е. равно числу сочетаний Полученное равенство называют формулой Бернулли. Пример 3.13. Вероятность изготовления на станке-автомате нестандартной детали равна 0,02. Какова вероятность того, что среди наудачу взятых шести деталей окажется более четырех стандартных? Решение. Вероятность того, что наудачу взятое изделие окажется нестандартным равна q=0,02. Вероятность того, что изделие окажется стандартным равна p=1–q=0,98. Поскольку эти вероятности постоянны и не изменяются от испытания к испытанию, то для подсчета вероятности можно применить формулу Бернулли. Появление более четырех стандартных изделий означает, что среди 6 взятых деталей окажутся 5 или 6 стандартных. Следовательно = 50,9850,021 + 10,9860,020 0,9943. 3.7. Локальная теорема Муавра-ЛапласаНесмотря на элементарность формулы Бернулли, при больших n непосредственное вычисление по ней связано с большой вычислительной работой, особенно если требуется не просто вычислить вероятность Pn(m) при конкретных значениях n и m, а решить какую-либо экстремальную задачу. Поэтому широкое значение получили приближенные асимптотические формулы. Функция g(x) называется асимптотическим приближением функции f(x), если Локальная теорема Муавра-Лапласа. Если в схеме Бернулли число испытаний n велико, при этом npq » 1,то справедлива приближенная формула где Ввиду важности функции (x), которая называется плотностью стандартного нормального распределения, для нее составлены специальные таблицы. При использовании таблиц следует учитывать, что функция (x) четная, т.е. (–x)=(x). Доказательство. Одно из доказательств локальной теоремы основано на использовании формулы Стирлинга: при n. Не даваясь в математические подробности доказательства, изложим основную его суть. Будем считать, что числа m и n–m в формуле Бернулли возрастают до бесконечности вместе с n. Тогда после применения формулы Стирлинга формула Бернулли примет вид Рассмотрим теперь величину Положим Поскольку при больших n величины 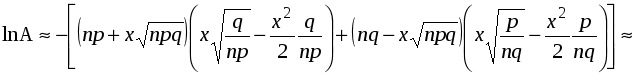 Следовательно, Наконец, учитывая, что Принимая во внимание все это, получим утверждение теоремы. Теперь приведем некоторые рекомендации (носящие, вообще говоря, условный характер) по применению теоремы Муавра-Лапласа. 1) Если n=1020, то теорема Муавра-Лапласа используется для грубых оценок. 2) Если n=20100, то приближенные формулы уже можно использовать для прикладных инженерных расчетов. 3) Если n=1001000, то практически в любых инженерных расчетах можно обойтись приближенными асимптотическими формулами. 4) Если n>1000, то даже специальные таблицы рассчитываются с помощью асимптотических формул (правда, для увеличения точности используют специальные поправки). Здесь следует еще добавить, что локальная формула Муавра-Лапласа верна с точностью до Отметим также, что из условий теоремы следует, что если n, то и m. Это означает, что n и m должны отличаться друг от друга не очень сильно, например, для Pn(0) теорема Муавра-Лапласа дает плохое приближение. Прежде чем переходить к рассмотрению примеров, скажем несколько слов о погрешностях, возникающих при использовании приближенных формул. Отметим, что полученная формула гарантирует только малую абсолютную погрешность, а относительная погрешность может быть сколь угодно большой; причем относительная погрешность увеличивается с ростом абсолютного значения |x| = Пример 3.14. Производится 10 подбрасываний монеты. Найти вероятность того, что выпадет ровно m (m=0,1,...,10) "гербов". Решение. Вычислим точные значения искомых вероятностей по формуле Бернулли: После этого воспользуемся локальной теоремой Муавра-Лапласа. Поскольку Результаты вычислений P10(m) занесем в таблицу.
Из таблицы видно, что приемлемые результаты приближенных вычислений находятся в середине таблицы. В целом можно отметить, что применение локальной теоремы в данной задаче не оправдано. Отметим, что сравнение точных и приближенных вычислений связано со сравнением биномиального и нормального распределений (см. темы: «Биномиальное распределение» и «Центральная предельная теорема») Пример 3.15. Вероятность того, что сошедшая с конвейера деталь стандартная равна 0,9. Найти вероятность того, что из 400 сошедших с конвейера деталей 356 окажутся стандартными. Решение. Согласно условию задачи: n=400, m=356, p=0,9, q=0,1. Поскольку n>100 и npq=36>10, то можно применить теорему Муавра-Лапласа. Найдем После этого находим значение функции (–0,6667)=0,31945. В результате, получаем Компьютерные вычисления при помощи формулы Бернулли дает следующий результат P400(356) = 0,05127. Видно, что применение в данной задаче локальной теоремы Муавра-Лапласа было практически оправдано. 3.8. Интегральная теорема Муавра-ЛапласаВ рассмотренном выше примере вероятность получилась довольно малой, несмотря на то, что вероятность появления стандартной детали равна 0,9. Это объясняется тем, что была вычислена вероятность только одного из 401 исходов. Поэтому в практических приложениях представляет интерес вычисления не одного, а нескольких исходов. Такую вероятность можно получить путем суммирования по всем возможным исходам m. Однако при больших n и достаточно широких пределов изменения величины m вычисления будут довольно громоздкими. В этих случаях для приближенных вычислений используется Интегральная теорема Муавра-Лапласа. Если в схеме Бернулли число испытаний n велико, то для вероятности Pn(k1mk2) того, что число успехов заключено в пределах от k1до k2, справедливо приближенная формула где Отметим, что функция Лапласа – нечетная функция, т.е. Ф(–x) = –Ф(x), для которой составлены специальные таблицы. Обратите внимание, что 0Ф(x)0,5. Доказательство теоремы проведем, опираясь на локальную теорему Муавра-Лапласа (здесь мы также опускаем отдельные технические детали доказательства). Очевидно, что вероятность Pn(k1mk2) можно представить в виде  . .Так как то сумму можно написать в виде  , ,которая мало чем отличается от подходящим образом выбранной интегральной суммы, соответствующей интегралу 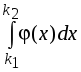 . Следовательно, . Следовательно,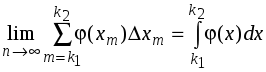 . .Таким образом, 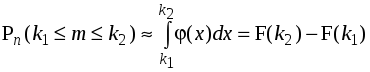 , ,где Пример 3.16. В среднем в ОТК бракуется 10% изделий. На контроль отобрано 625 изделий. Какова вероятность того, что среди них не менее 550 и не более 575 стандартных изделий? Решение. По условию задачи n=625, p=0,9, q=0,1, k1=550, k2=575. Поскольку npq=56,25»1 и n=625>100, то искомую вероятность найдем при помощи интегральной формулы Муавра-Лапласа: = 2·0,45221 = 0,90442. Более точные компьютерные вычисления, с использованием формулы Бернулли, дают следующий результат P625(550m575) = 0,90431. Видно, что использование интегральной теоремы Муавра-Лапласа было вполне оправданным. 3.9. Теорема ПуассонаПри использовании теорем Муавра-Лапласа можно заметить, что она действует тем "хуже", чем больше вероятность p отличается от 1/2, т.е. чем ближе вероятность к 1 или 0. Однако значительное число задач связано с необходимостью вычисления вероятностей Pn(m) именно при малых значениях p (или q). Теорема Пуассона. Если в схеме Бернулли число испытаний n велико, а вероятность успеха p в одном испытании мала, причем мало также произведение np, то справедлива приближенная формула где = np. Доказательство. Запишем формулу Бернулли или, с учетом обозначения = np, p = /n: Известно, что Кроме того, если n велико, то что и требовалось доказать. Отметим, что формула Пуассона справедлива также по отношению к числу неудач, но только в том случае, когда мало = nq. Теперь рассмотрим некоторые рекомендации по применению приближенной формулы Пуассона. 1) Если число испытаний n=1020, то теорема Пуассона используется для грубых оценок, когда = np или = nq изменяются в пределах от 02 (при n=10) до 03 (при n=20); в противном случае необходимо пользоваться формулами Муавра-Лапласа. 2) Если n=20100, то формулу Пуассона рекомендуется применять, когда и заключаются в следующих пределах: от 03 (при n=20) до 05 (при n=100). 3) Если n=1001000, то формула Пуассона используется, когда и изменяются в следующих пределах: от 05 (при n=100) до 010 (при n=1000). 4) Если n>1000, то необходимо чтобы и лежали в пределах 010 и более. Еще раз отметим, что приближенные формулы Пуассона и Муавра-Лапласа гарантируют только малую абсолютную погрешность, но не относительную погрешность. Пример 3.17. Счетчик Гейгера регистрирует попадание в него -частицы с вероятностью p=0,9. Найти вероятность того, что он зарегистрировал m (m=0,1,2,...,10) частиц при условии, что в него попало n=10 частиц. Решение. Воспользуемся сначала точной формулой Бернулли, в соответствии с которой После этого воспользуемся приближенной формулой Пуассона. В данном случае = np =9 – велико, а = nq = 1 мало. Это значит, что нужно воспользоваться формулой Пуассона, но по отношению к незарегистрированным частицам. В соответствии с этой формулой Результаты вычислений P10(m) занесем в таблицу.
Анализируя приведенные результаты, видно, что максимальная абсолютная погрешность невелика, чего нельзя сказать о максимальной относительной погрешности. Если в данной задаче воспользоваться локальной теоремой Муавра-Лапласа (чего не рекомендуется делать, поскольку npq=0,9 сравнимо и даже меньше единицы), то получим результаты, имеющие существенно большие погрешности. Пример 3.18. Радиоаппаратура состоит из 900 элементов. Вероятность отказа одного элемента в течение года работы равна p=0,001 и не зависит от состояния других элементов. Какова вероятность отказа не менее двух элементов за год? Решение. Поскольку =np=0,9, то можно применить теорему Пуассона. Тогда  Точное значение практически не значительно отличается от приближенного. Следовательно, в данной задаче допустимо применение формулы Пуассона. |
