|
|
Основы физики горения, лекция 5. Лекция Ламинарное распространение пламени
Лекция 5. Ламинарное распространение пламени
Распространение экзотермических реакций в газовых смесях чаще всего происходит при наличии значительных градиентов температур и концентраций. При этом течение смеси может быть как турбулентным, так и ламинарным, что определяется начальными и граничными условиями и характерными размерами и скоростями движения смеси. Распространение химических реакций в ламинарном режиме [течения] имеет наиболее простой характер и представляет собой в простейшем случае движущийся вверх по потоку горючей смеси относительно тонкий фронт ламинарного пламени. Интенсивность процесса горения в этом случае лимитируется как химико-кинетичскими факторами, так и процессами молекулярного переноса тепла и вещества.
Основные особенности горения во фронте ламинарного пламени
Ламинарное пламя – фронт волны нормального (не детонационного) горения в газовой смеси в отсутствие эффектов турбулентности.
Явление горения во фронте ламинарного пламени занимает одно из центральных мест в теории горения. Это наиболее доступное для теоретического описания явление, для изучения которого, однако, уже требуется совместное рассмотрение химических реакций и переноса в движущейся смеси. Знание основных особенностей этого явления и знакомство с моделями, привлекаемыми для его описания весьма полезно для изучения более сложных процессов, связанных с горением, таких как горение в турбулентном потоке, гетерогенное горение, детонация.
Вначале ограничимся горением полностью перемешанных гомогенных горючих смесей. Рассмотрим два классических примера ламинарного горения.
Распространение фронта реакции в неподвижной смеси. Если холодную неподвижную горючую смесь подогреть локально некоторым источником тепла (напр., эл. разрядом), то в соответствии с природой химических реакций, в окружающем микрообъеме многократно возрастут скорости химических реакций и начнется интенсивное тепловыделение. Под действием теплопроводности и диффузии активных центров [радикалов] в слоях смеси, отделяющих нагретые п. с. от с. с., будет инициироваться химические превращения и реакция, таким образом, волна химического превращения будет распространяться в ближайшие слои смеси в виде фронта ламинарного пламени. В результате вся с. с. в выделенном объеме довольно скоро превратится в п. с. (рис 5.1).

Рис. 5.1. Распространение фронта ламинарного горения в неподвижной смеси
Процесс ламинарного горения, называемый еще нормальным горением, или горением во фронте, характеризуется послойным выгоранием смеси, в отличие от объемного сгорания, когда смесь нагревается и реагирует одновременно, и от турбулентного горения, когда турбулизированная среда искривляет и разрывает фронт горения, тем самым интенсифицируя сгорание.
Ламинарное горение смеси в стационарном потоке. Классический пример стационарного ламинарного пламени – горение с. с., вытекающей в ламинарном режиме из трубки – горелка Бунзена (рис. 5.2.):

Рис. 5.2. Ламинарное пламя на срезе горелки Бунзена.
В данном случае изображенный фронт пламени, в котором начинаются, проходят и (в основном) заканчиваются реакции, достаточно тонок, и имеет форму, приближающуюся к конической. Продукты сгорания ниже по потоку обладают значительной температурой и создают свечение, зрительно увеличивая факел пламени.
Положение пламени на срезе горелки устойчивое, если скорость потока заключена в некотором диапазоне. При достаточно малой скорости потока конус укорачивается и может наблюдаться “проскок” пламени внутрь трубки. При большой скорости может иметь место срыв пламени, в некоторых случаях срыва пламени (в ламинарном режиме) не происходит вследствие перехода режима течения и горения потока в турбулентный.
Нормальная скорость горения. В обоих рассмотренных примерах толщина зоны горения весьма мала по сравнению с характерными размерами системы. Такое предположение часто бывает оправданным, поэтому в ряде случаев удобно считать фронт ламинарного горения бесконечно тонкой поверхностью, положение которой в каждый момент определяется полем скоростей потока. При этом действительный фронт пламени заменяется “тепловым скачком”, на котором терпят разрыв температура и состав смеси.
Нетрудно видеть, что проекция относительной скорости потока на нормаль к поверхности пламени должна быть примерно постоянной во всех точках. Эта величина, обозначаемая un, носит название нормальной скорости горения и является важной интегральной константой, характеризующей интенсивность горения смесей при заданных составе и параметрах состояния. Утверждение о том, что проекция скорости набегающей смеси относительно пламени на перпендикулярное пламени направлении постоянна и равна un, называется законом Михельсона.
Форма фронта пламени на срезе горелки (рис 5.2.) в соответствии этим правилом может быть приближенно найдена по известному распределению скорости потока в горелке и заданной un.
Структура фронта ламинарного пламени. В рамках допущения о тонкости фронта пламени невозможно, однако, определение его количественных характеристик, за исключением некоторых интегральных (состав и температура п. с.). Так, уже для теоретического определения величины un требуется рассматривать внутреннюю структуру фронта ламинарного пламени. Чтобы прийти к стационарной постановке, введем систему координат, связанную с фронтом пламени, приняв за x нормаль к поверхности пламени. Далее, при слабо искривленном фронте достаточно рассматривать одномерное распределение параметров в продольном направлении x (рис. 5.3).
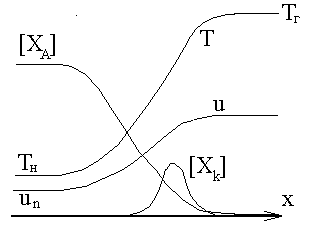
Рис. 5.3. Структура фронта ламинарного пламени.
Видно, что фронт пламени можно рассматривать как волну, во фронте которой происходит нагрев смеси теплопроводностью, протекают и заканчиваются химические реакции. Профиль температуры T(x) монотонно изменяется между крайними значениями Tн и Tг, состав смеси претерпевает сложные изменения вследствие наличия одновременно протекающих реакций и диффузии: находящиеся в избытке реагенты ([XA]) расходуются не полностью, концентрации промежуточных компонентов ([Xk]) достигают максимума в окрестности зоны интенсивных химических превращений. Вследствие многократного падения плотности, в соответствии с законом сохранения массы, увеличивается проекция относительной скорости смеси на нормаль к фронту u(x), при этом начальное значение этой скорости un равно нормальной составляющей относительной скорости потока.
Расчет нормальной скорости горения по тепловой теории
Небольшая толщина фронта ламинарного пламени в предварительно перемешанной смеси и, соответственно, высокие значения градиентов параметров, указывают на то, что процессы молекулярного переноса – диффузия и теплопроводность – в значительной мере лимитируют скорость un, а значит и интенсивность переработки с.с. в п.с. в ламинарном пламени. Оказывается, на основе упрощений основных уравнений гидродинамики реагирующих потоков могут быть построены теоретические модели, позволяющие с хорошей точностью рассчитывать структуру, оценивать толщину фронта пламени и нормальную скорость un. К числу таких моделей, принимающих во внимание как кинетические аспекты, так и явления молекулярного переноса, относится теория ламинарного пламени Я. Б. Зельдовича, Д. А. Франк-Каменецкого и Н. Н. Семенова.
Теоретические работы по исследованию ламинарного горения начались еще в 1883 г, когда Малляр и Ле-Шателье попытались вывести расчетную формулу для нормальной скорости. Только в 1938 г. Я. Б. Зельдович и Д. А. Франк-Каменецкий разработали т. н. тепловую теорию ламинарного пламени, в которой удалось связать скорость un с кинетикой горения и теплопроводностью смеси. Позднее теория получила развитие в работах Я. Б. Зельдовича и Н. Н. Семенова. Благодаря простоте и наглядности конечных расчетных формул она считается классической несмотря на то, что позднее появились более полные решения. Ниже приводится вывод формулы для расчета un, в основном повторяющий вывод основной формулы теории З., Ф.-К., С.
При рассмотрении одномерной движущейся волны реакции исходная система уравнений в общем случае имеет вид (см. 4.4, 4.11а, 4.17):
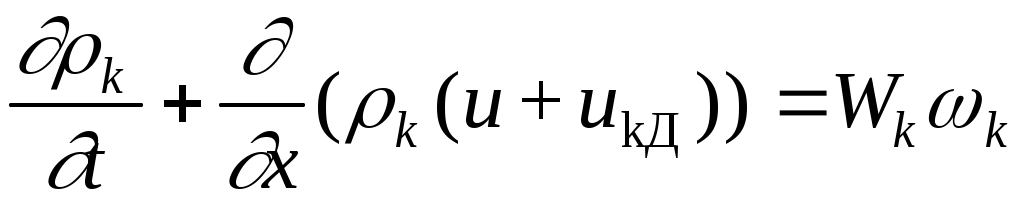 , ,
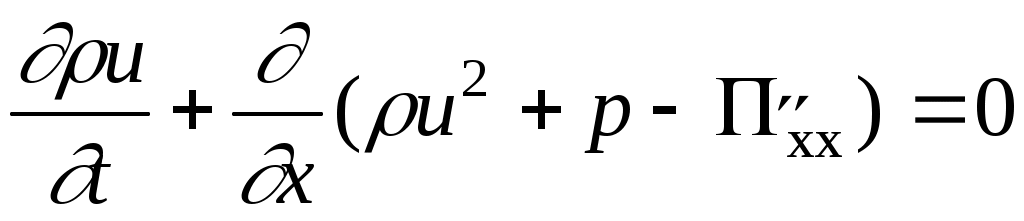 , ,
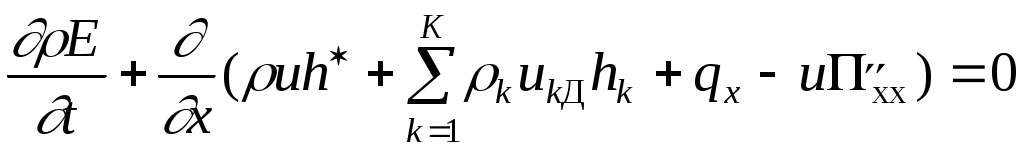 . .
Для упрощения системы уравнений сделаем следующие обоснованные допущения.
1. Перейдем к системе координат, связанной с фронтом пламени, в этом случае следует применять стационарную форму законов сохранения.
2. При реально имеющих место невысоких скоростях un изменение статического давления при переходе через фронт пламени пренебрежимо мало. Легко показать, что
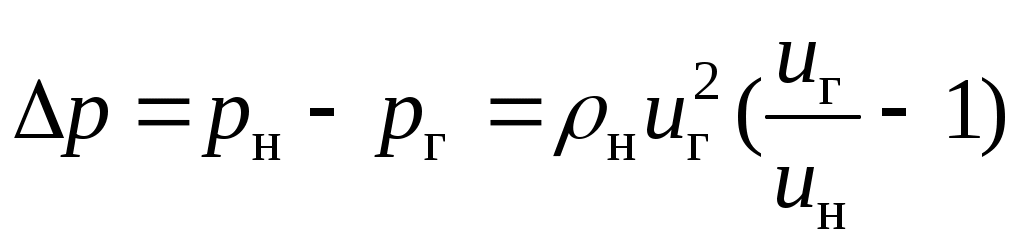 . .
Поэтому уравнение количества движения можно исключить из рассмотрения.
3. Изменение скорости (uг–un) при переходе через фронт также невелико, поэтому вместо энтальпии торможения h*в уравнении энергии можно использовать статическую энтальпию h = h – 0,5 u2, а также правомерно пренебречь членом 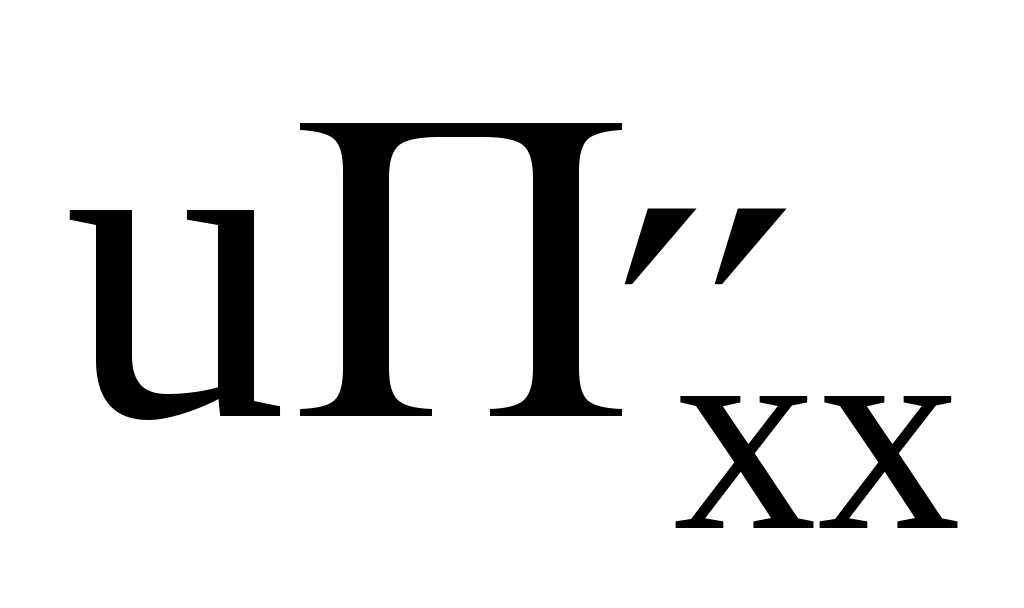 (работа вязких напряжений) в уравнении энергии. (работа вязких напряжений) в уравнении энергии.
С учетом этих допущений основная система уравнений запишется в виде:
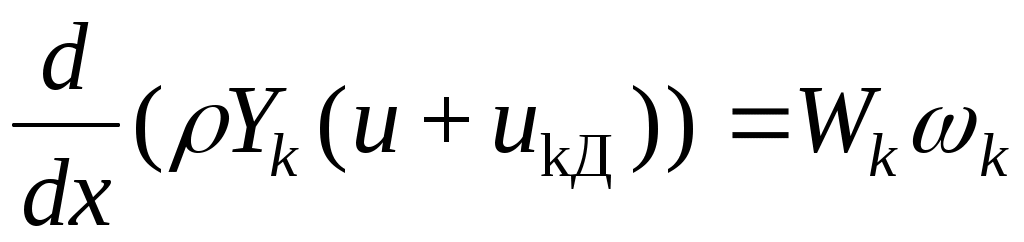 , k = 1...K, , k = 1...K,
 . .
Уравнение сохранения массы смеси получим, сложив все k = 1...K уравнений сохранения массы компонентов. Имеем:
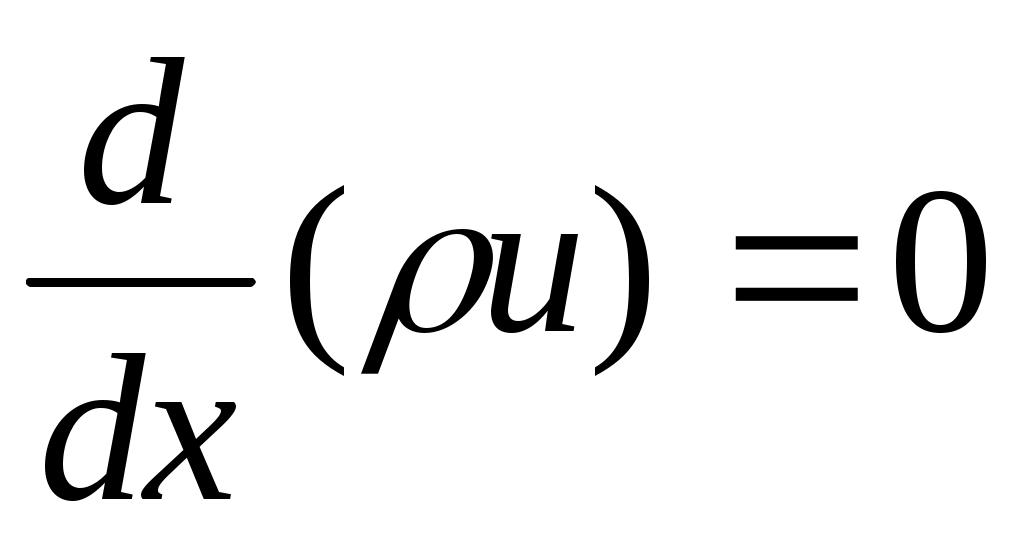 или или 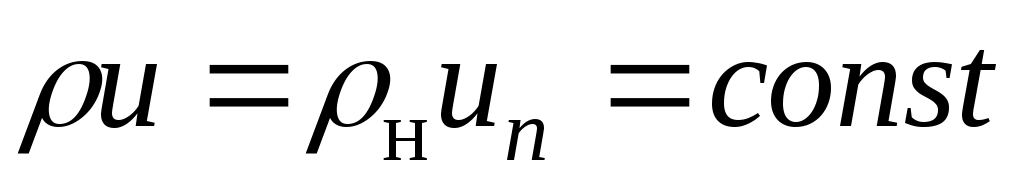 . .
Определим энтальпию каждого компонента как 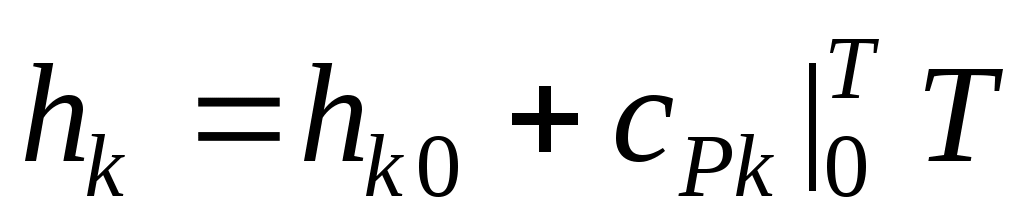 , причем, для всех компонентов, кроме одного (условно- “топливо” A), находящегося в избытке , причем, для всех компонентов, кроме одного (условно- “топливо” A), находящегося в избытке  , а для топлива А , а для топлива А  . Кроме того, пусть для всех K компонентов зависимости изобарной удельной теплоемкости от T . Кроме того, пусть для всех K компонентов зависимости изобарной удельной теплоемкости от T  будут одинаковыми. Тогда уравнение энергии можно преобразовать так: будут одинаковыми. Тогда уравнение энергии можно преобразовать так:

Из уравнения сохранения массы компонента А можно установить, что
 , после чего уравнение энергии приводится к виду: , после чего уравнение энергии приводится к виду:
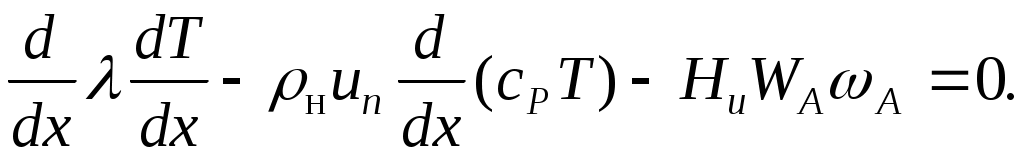 (5.1) (5.1)
В этом уравнении un – неизвестный параметр, подлежащий определению. Задав определенную зависимость суммарной скорости образования А от температуры и текущего состава, можно найти un, применяя численное интегрирование дифференциального уравнения (5.11).
Однако можно, учитывая некоторые особенности протекания химических реакций, найти решение более простым путем. А именно, выделим в структуре фронта пламени две зоны (рис. 5.6). Считаем, что в зоне I химических реакций нет и справедливо уравнение (5.11) без слагаемого  . Для зоны II считаем возможным пренебречь вторым слагаемым (5.11) по сравнению с двумя другими. Решения в обеих зонах состыкуем между собой в точке с температурой Tв (“точке воспламенения”), используя условие равенства пространственных производных температуры в этой точке . Для зоны II считаем возможным пренебречь вторым слагаемым (5.11) по сравнению с двумя другими. Решения в обеих зонах состыкуем между собой в точке с температурой Tв (“точке воспламенения”), используя условие равенства пространственных производных температуры в этой точке
 . .

Рис. 5.6. Две зоны в структуре фронта ламинарного пламени.
Таким образом, для зоны I имеем:
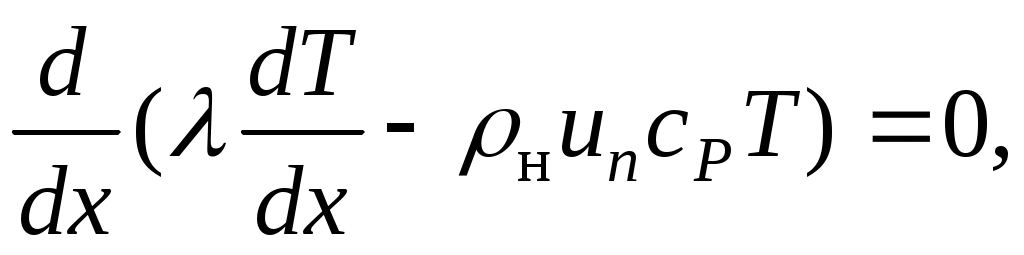
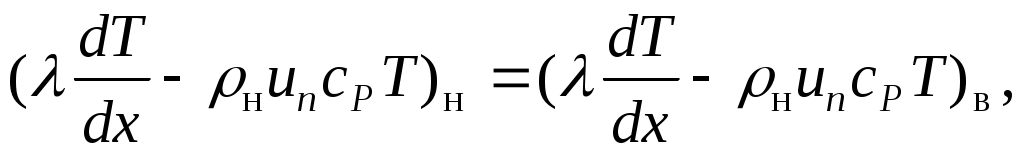 но поскольку но поскольку  , то , то
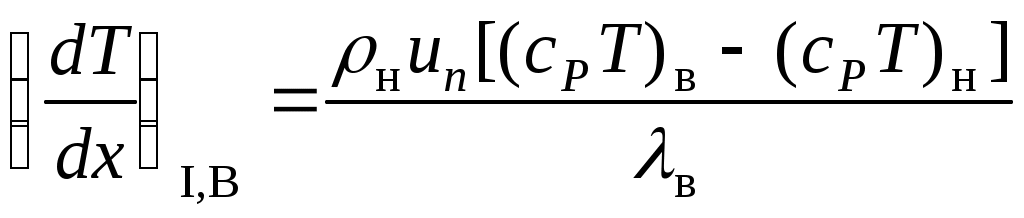 . (5.2) . (5.2)
Для зоны II, вводя обозначение  , из (5.1) без второго слагаемого имеем: , из (5.1) без второго слагаемого имеем:

Считая приближенно г = const, проинтегрируем:
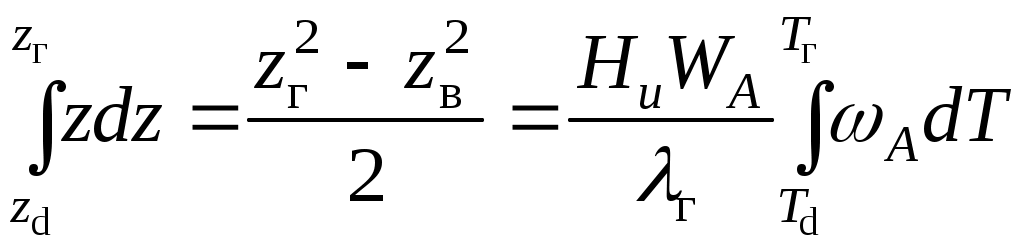 , но поскольку , но поскольку 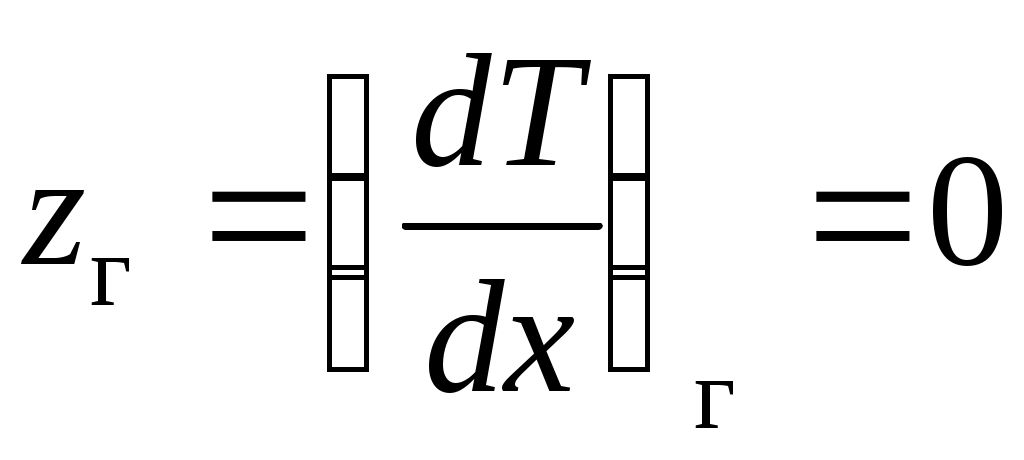 , то , то
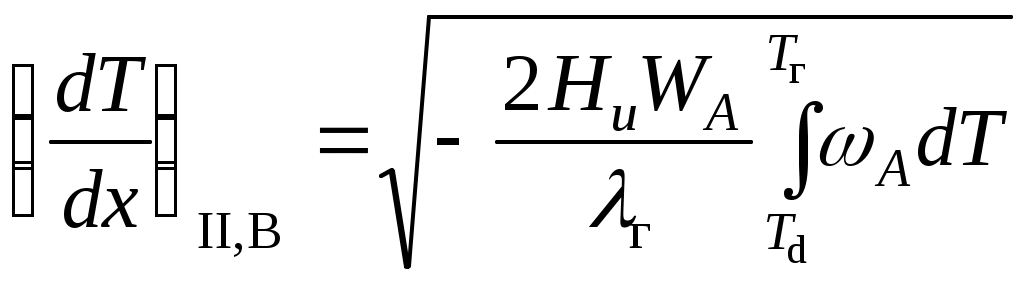 . (5.3) . (5.3)
Приравнивая (5.2) и (5.3), получаем основную формулу теории З.,Ф.-К.,С – формулу расчета un:
 . (5.4) . (5.4)
Чтобы воспользоваться формулой (5.4), следует определить правдоподобное значение Tв и задать способ вычисления интеграла в (5.4), представляющего суммарное влияние химических реакций. В теории З.,Ф.-К.,С для определения Tв применяется выражение для характеристического интервала температур:
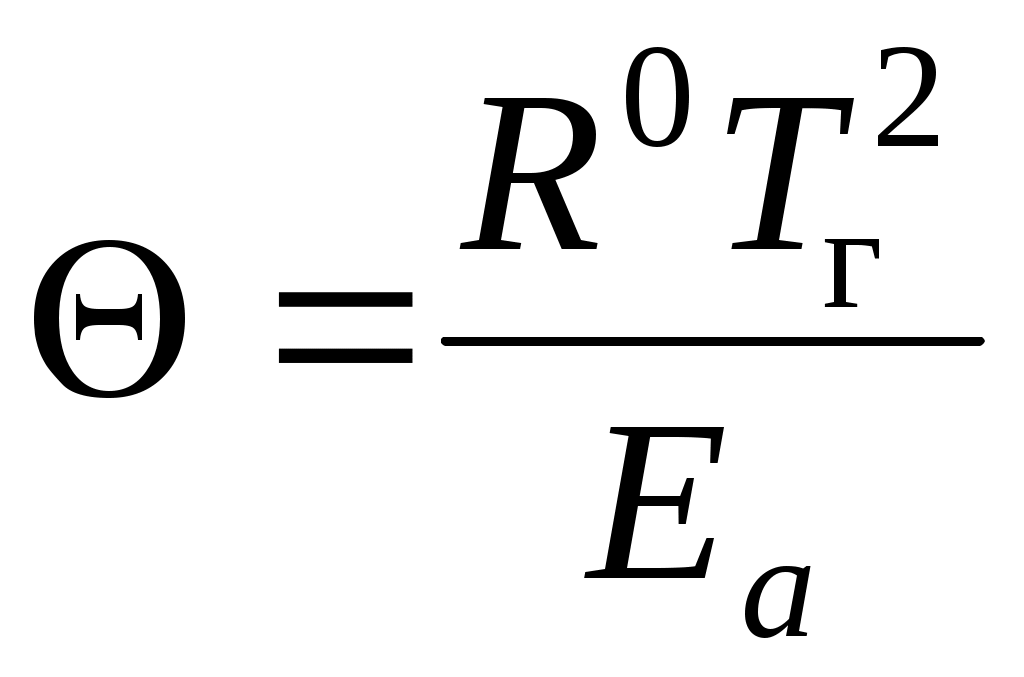 , ,
для которого, при Tв = Tг - для реакций 1-го и при Tв = Tг - 2 для реакций 2-го порядка можно пренебречь скоростями реакций при T < Tв.
Для вычисления интеграла в (5.4), в котором A– функция температуры, удобнее всего выразить профили концентраций через профили температуры (в простейших случаях данный интеграл берется аналитически). Действительно, при определенных условиях можно принять, что профили температур и массовых долей компонентов, находящихся в избытке, подобны. Докажем это.
Сравнивая уравнения сохранения массы компонента A и уравнение энергии смеси:
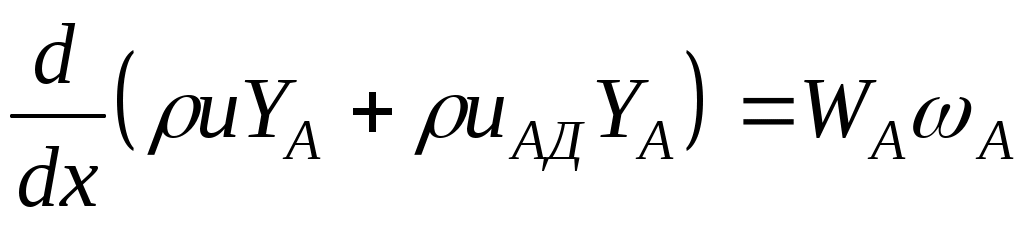 , ,
 , (получено из (5.1)) , (получено из (5.1))
можно заметить, что если обозначить 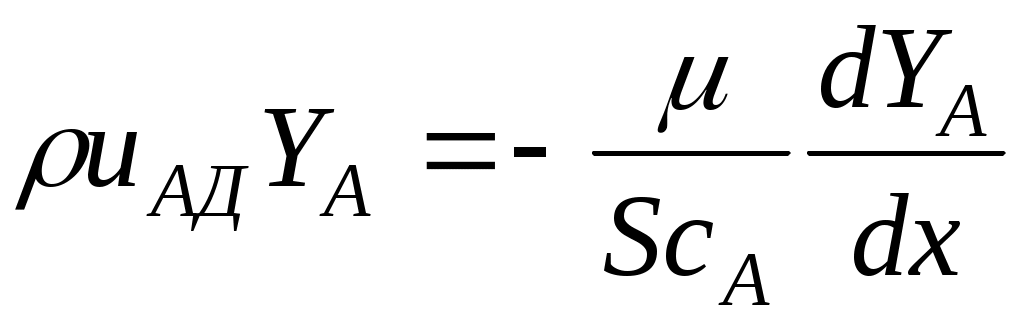 , а также принимая во внимание, что , а также принимая во внимание, что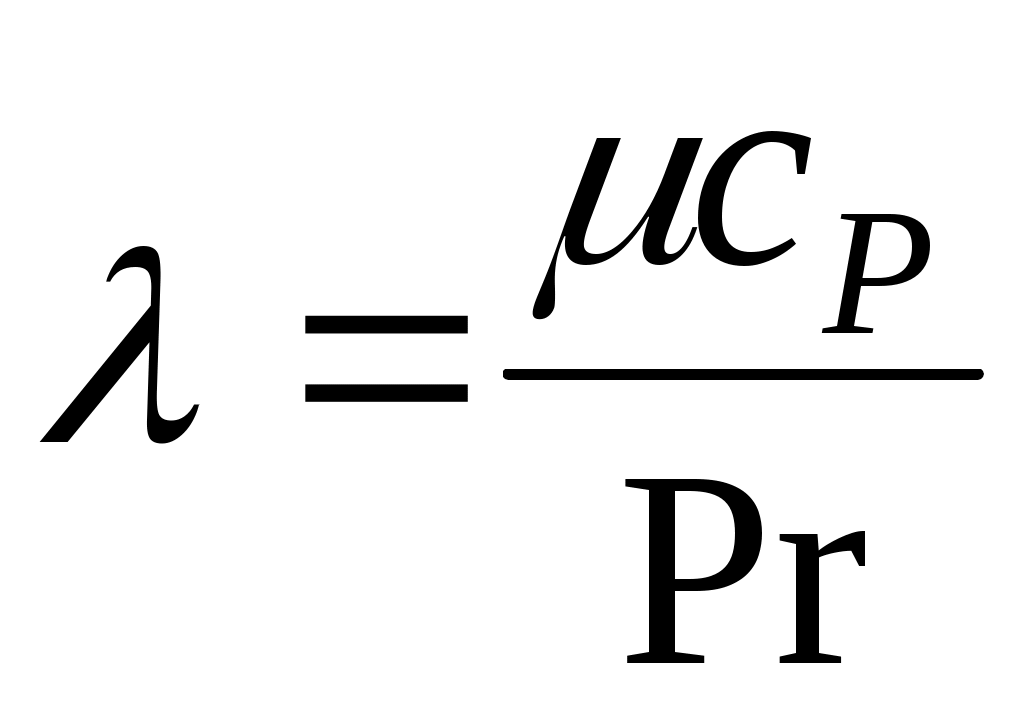 , а также использовать еще более сильное допущение о том, что теплоемкость смеси cP не зависит от температуры (cP = const), т. е. , а также использовать еще более сильное допущение о том, что теплоемкость смеси cP не зависит от температуры (cP = const), т. е. 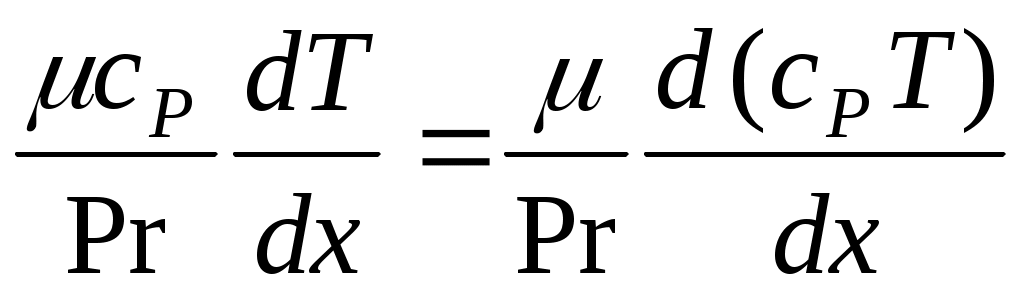 и деля уравнение энергии на – Hu (= const!), то получим: и деля уравнение энергии на – Hu (= const!), то получим:
 , ,
 , (получено из (5.1)) , (получено из (5.1))
Если теперь принять еще одно допущение, а именно, что ScA = Pr (т. е. 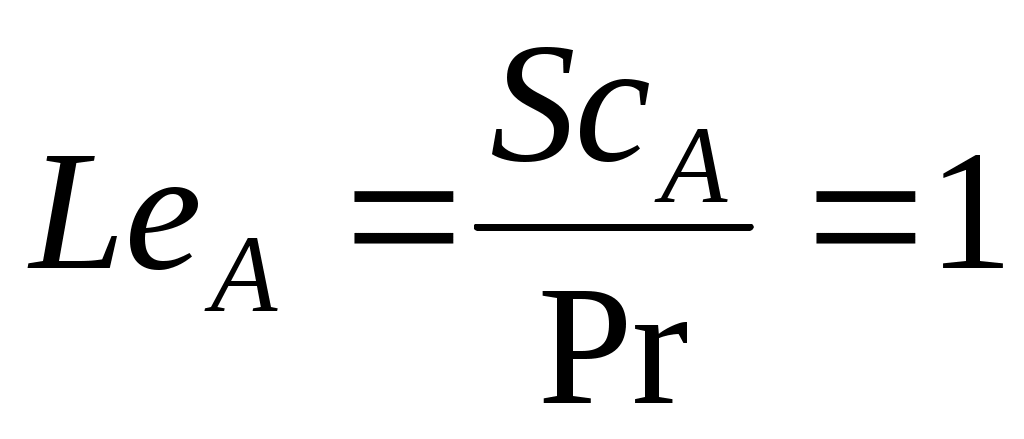 ), становится очевидным, что профили параметров YA и ), становится очевидным, что профили параметров YA и 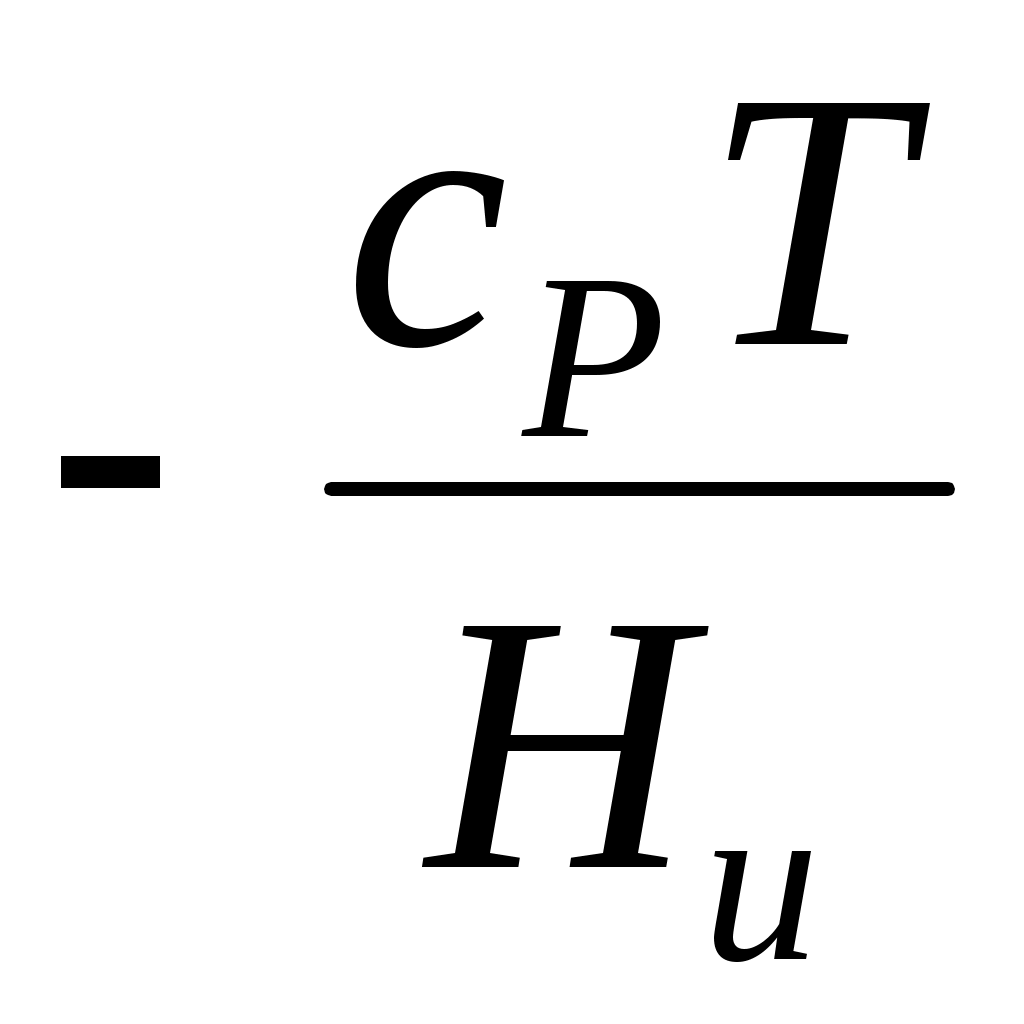 подчиняются идентичным уравнениям, следовательно, они подобны (рис. 5.7), поэтому: подчиняются идентичным уравнениям, следовательно, они подобны (рис. 5.7), поэтому:
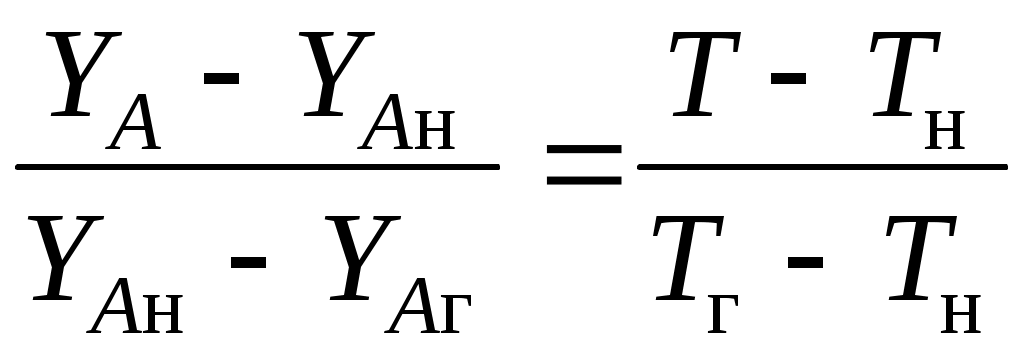 . .

Рис. 5.7. Подобие профилей YA и –T во фронте ламинарного пламени.
Действительно, приближенное подобие профилей YA и 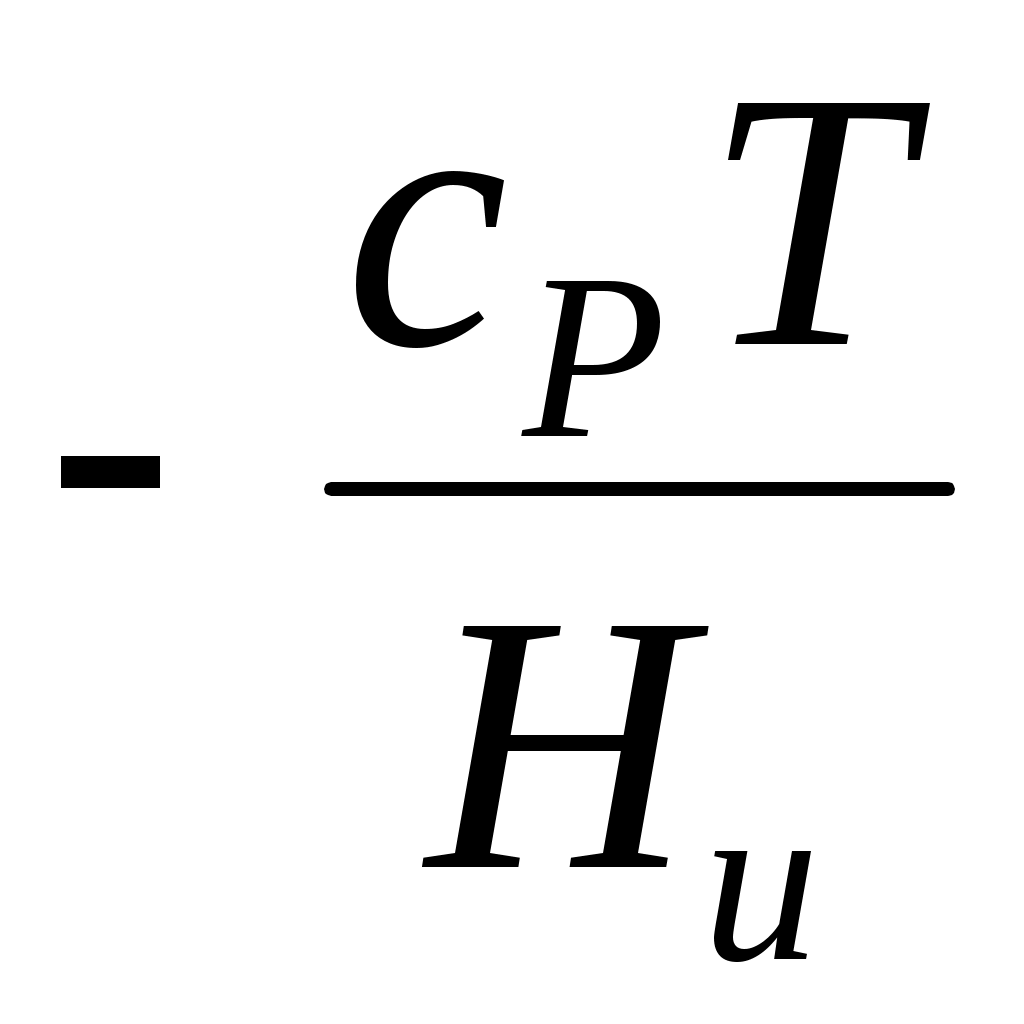 имеет место в реальных задачах. Задание концентраций по профилям температур значительно облегчает вывод подынтегрального выражения для подстановки в формулу (5.4). имеет место в реальных задачах. Задание концентраций по профилям температур значительно облегчает вывод подынтегрального выражения для подстановки в формулу (5.4).
Оценка толщины фронта ламинарного пламени, пусть довольно условная, может быть сделана по выражению:
 , (5.5) , (5.5)
полученному с помощью (5.2). Здесь толщина пламени bф определяется как длина подкасательной к профилю T, проведенной в точке TВ. Для обычных горючих смесей в обычных условиях по (5.5) получаются величины порядка нескольких десятых долей миллиметра, что удовлетворительно согласуется с экспериментами.
Эффект Махе при сгорании в замкнутом объеме. Если сгорание в замкнутом объеме происходит во фронте пламени и не сопровождается интенсивным перемешиванием п. с. и с. с., то после его окончания объем оказывается заполнен п. с. с повышенным давлением и неодинаковой местной температурой: температура первых порций п. с. оказывается на несколько сот градусов выше. Данное явление – неравномерное распределение температуры по объему п. с. при сгорании при v const носит название эффекта Махе.
Объяснение данного эффекта состоит в том, что температура порций с. с., сгорающих первыми, вначале повышается от Тн до Тг, затем, при общем повышении давление от pн до p’к, подвергаются [адиабатическому] сжатию от Тг до Т’г. Для последних порций последовательность обратная: сначала сжатие от Тн до Тк, затем сгорание – от Тк до Т’к. Так как повышение температур при сгорании в обоих случаях примерно одинаково Тг –Тн Т’г –Т’к, а работа адиабатного сжатия возрастает с увеличением начальной температуры, то порции, сгорающие первыми, запасают больше внутренней энергии, следовательно их температура Т’г оказывается выше, чем Т’к (рис. 4.4).
Ламинарное диффузионное горение. Особым образом сгорают в ламинарном потоке предварительно не перемешанные реагенты. В этом случае реагенты перемещаются в зону реакции (представляющую собой более или менее тонкий разделяющий фронт) под действием молекулярной диффузии. Зона реакции устанавливается примерно в области, отвечающей стехиометрии. На рис. 5.5. показано ламинарное диффузионное горение не смешанных первоначально газообразных топлива и окислителя в стабилизированном ламинарном диффузионном пламени.
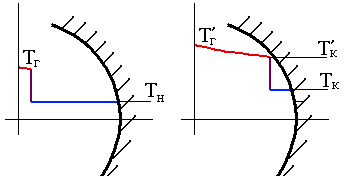
Рис. 5.4. К объяснению эффекта Махе.

Рис. 5.5. Ламинарное диффузионное пламя.
Экспериментальные данные по нормальным скоростям горения
Нормальная скорость горения un – важный и наглядный суммарный показатель горючей смеси, достаточно очевидно определяемый экспериментальным путем. Многое и механизме и природе химических превращений в ламинарном пламени можно узнать, зная величину un и ее зависимость от режимных параметров. Поэтому в многочисленных экспериментальных работах изучалось изменение un в зависимости от начальных параметров и состава смеси.
Рассмотрим возможные методики и результаты экспериментов по определению un, проливающие свет на особенности процессов горения смесей в ламинарном фронте.
Методы экспериментального измерения un. Имеющиеся простые и наглядные методы экспериментального измерения un по существу предполагают bф 0. Перечислим здесь основные методы, вместе с их особенностями и недостатками.
1. Методы, основанные на измерении видимой скорости перемещения пламени в трубках.
Эта группа методов не позволяет точно измерить скорость перемещения фронта вследствие больших методических погрешностей, вызываемых неоднородностью полей скорости при течении в трубке и наличием не учитываемых тепловых потерь; представляют лишь исторический интерес.
2. Методы, основанные на применении “бомб” постоянного давления (например, заполненных горючей смесью мыльных пузырей). В этом случае видимая скорость пламени определяется посредством измерением (путем фотографирования, часто теневыми методами) увеличивающегося радиуса пузыря или области п. c.
Недостатки подобных методов заключаются в неконтролируемой влажности смеси вследствие испарения мыльной пленки, ее неустойчивости при некоторых температурах и давлениях и проницаемости.
3. Методы, основанные на использовании “бомб” постоянного объема. Эксперименты такого рода, с одновременным фотографированием фронта пламени и измерением давления в бомбе от времени, позволяют избежать некоторых методических погрешностей. Это касается измерений, проведенных в отсутствие заметного влияния эффекта Махе.
4. Методы измерения по конусу пламени на срезе бунзеновской горелки. Существует противоречие между стремлением увеличить диаметр горелки для снижения погрешности из-за конечной ширины пламени и пределом режима ламинарного течения по числу Re. Также имеются сложности с точным измерением величины местного наклона конуса пламени к оси горелки.
Во всех случаях конечная толщина фронта пламени искажает результаты экспериментов. Стремление уменьшить относительную ширину фронта пламени в эксперименте приводит к увеличению характерного времени, что увеличивает потери тепла из зоны п. с., например, излучением. Определение скорости пламени как скорости начальных или конечных точек его структуры ведет к методическим погрешностям. В этом случае для уточнения метода, стремятся определить видимую скорость перемещения некоторой “эквивалентной” зоны в структуре пламени.
При использовании экспериментальных данных всегда следует обращать внимание на методику, по которой проводились эксперименты.
Влияние на un начальной температуры смеси Тн. Уже из основной формулы теории З.,Ф.-К.,С очевидно, что с увеличением Тн должна увеличиваться и скорость un. Действительно, величина подынтегрального выражения в формуле (5.4) при увеличении Тн и прочих равных условиях должно только увеличиваться. В экспериментах наблюдается примерно степенная зависимость un Т н 1,8 (что соответствует эффективному порядку реакций при сгорании большинства углеводородных топлив, который также близок к 1,8). На рис. 5.6. показана зависимость un (Т н), полученная экспериментально для смесей керосина и бензина с воздухом при =0,95 и p=1 атм. Для сравнения приведена та же зависимость, полученная расчетом по теории З.,Ф.-К.,С при Ea=40000 ккал/моль.
Рис. 5.6. Зависимость un (Т н) для смесей бензина с воздухом.
Конечно, при невозможности задать истинную кинетику процесса горения углеводородов, при применении формулы З.,Ф.-К.,С ограничиваются суммарной кинетикой единичной бимолекулярной реакции, причем константы в формуле для константы скорости могут быть хорошо подобраны, например, из условия лучшего соответствия экспериментальным данным типа изображенных на рис. 5.6. Примечательно то, что хотя бы интенсивность такого комплексного процесса, как ламинарное горение можно описать парой подобранных коэффициентов в модели типа З.,Ф.-К.,С!
Влияние на un давления смеси. Из теоретических построений следует, что вид зависимости un(p) напрямую зависит от молекулярности [лимитирующей] реакции в кинетической модели, описывающей окисление в данной смеси. Так, при =1 un
p-0,5, а при =2 un от давления не зависит. Вопрос о зависимости un(p) реальных углеводородов сложный, в частности, в частности, принимая вид этой зависимости показатель степени un
pm, мы столкнемся с тем, что показатель m принимает несколько отличающиеся значения в зависимости от температуры. В среднем, для обычных углеводородных топлив m = – (0,2…0,3), т. е. при повышении давления смеси нормальная скорость горения несколько снижается.
Влияние на un состава смеси. Состав горючей смеси из многих компонентов может варьироваться многими способами. Если, однако, выделить в смеси горючее, окислитель и инертный разбавитель, то будут представлять интерес изменения нормальной скорости горения un такой смеси при следующих подходах к изменению состава:
а) изменение при неизменном соотношении между горючим и разбавителем;
б) изменение относительной концентрации инертных веществ при =const;
в) замена одни инертные газы другими;
г) введение небольших добавок, заметно влияющих на скорости реакций.
Ниже будут рассмотрены экспериментальные данные, полученные для этих случаев.
а) изменение . Уже из общих соображений ясно, что при 1 реакции в соответствующей зоне будут протекать интенсивнее (главным образом вследствие увеличения температуры Тг), поэтому un()max именно при 1. В действительности максимум un() лежит обычно в пределах 0,90…0,96.
Ниже приведены графики un() для давлений p=0,1…1 ата, полученные экспериментально для пропано-воздушных смесей при комнатной температуре в диапазоне =0,5…1,5. Обращает на себя внимание несимметричность кривых un() относительно максимума и то, что un действительно снижается с повышением давления.
Рис. 5.7. Зависимости un() для смесей пропана с воздухом при разных p.
На рис. 5.8. – зависимости un() для смесей моноокиси углерода с кислородом, полученные при трех значениях давления. В данном случае кривые un (), которые можно построить по экспериментальным точкам, практически совпадают (!).
Рис. 5.8. Зависимости un() для смесей CO + O2 при p=200, 760 и 2530 мм. рт. ст.
Необходимо также помнить о существовании концентрационных пределов распространения пламени по . Сложно однозначно определить их, так как условия экспериментов несколько различаются. Можно определить абсолютные пределы по как пределы воспламеняемости смеси от стенки, нагретой до теоретической температуры пламени.
б) изменение относительной концентрации инертных веществ при =const. Для изучения суммарной кинетики, например, большое значение имеют данные экспериментов по влиянию на un относительной концентрации разбавителя (а также рода самого инертного разбавителя). На рис. 5.9. показаны результаты экспериментов по определению un для гексано-кислородно-азотных смесей.
Рис. 5.9. Зависимости un от доли топлива при различной массовой доле О2.
Расчеты, проведенные для этих случаев, показывают, что экспериментальные данные хорошо согласуются с формулами тепловой теории при Ea = 31600 кал/моль и бимолекулярном механизме, но лишь до 50% О2! Дальше рост Т г замедляется из-за диссоциации, и по расчету un возрастает быстрее, чем в эксперименте. Максимум с увеличением содержания О2 смещается в сторону бедных смесей, что также говорит об изменении механизма реакции при содержании в смеси более 50% О2.
в) замена одних инертных газов другими. Род разбавителя может оказывать заметное влияние на кинетику, особенно если является легко диссоциирующим газом.
г) введение небольших добавок, заметно влияющих на скорости реакций. Интересен вопрос о влиянии небольших количеств активных примесей на un.
Классический пример – добавление воды в смесь CO + O2. Экспериментально получено, что добавление малых доз паров воды в смесь увеличивает нормальную скорость пропорционально  и эта зависимость сохраняется до примерно и эта зависимость сохраняется до примерно 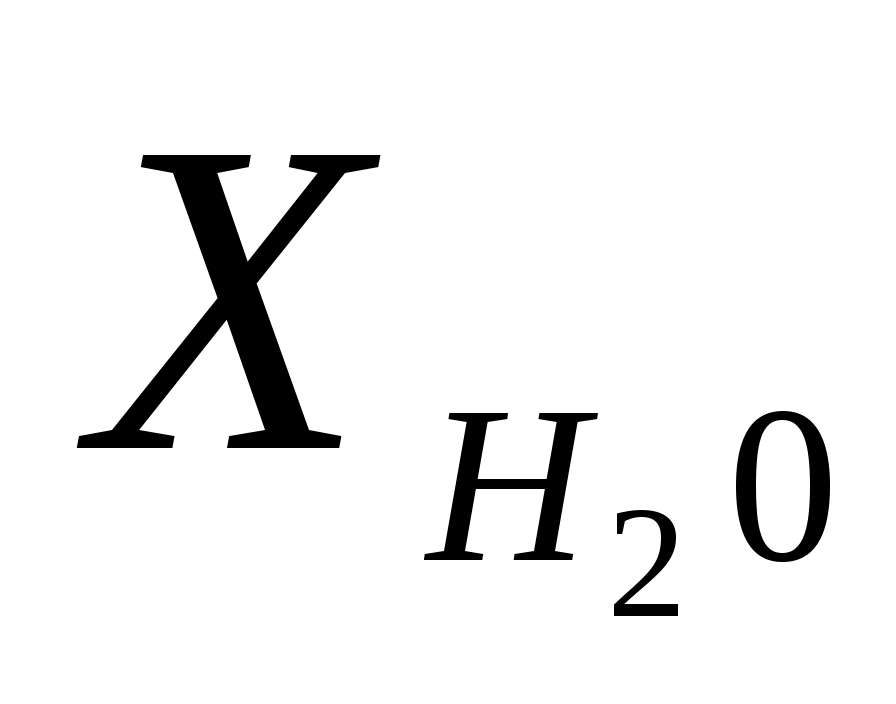 =4…5%, причем полное “насыщение” наступает при =4…5%, причем полное “насыщение” наступает при 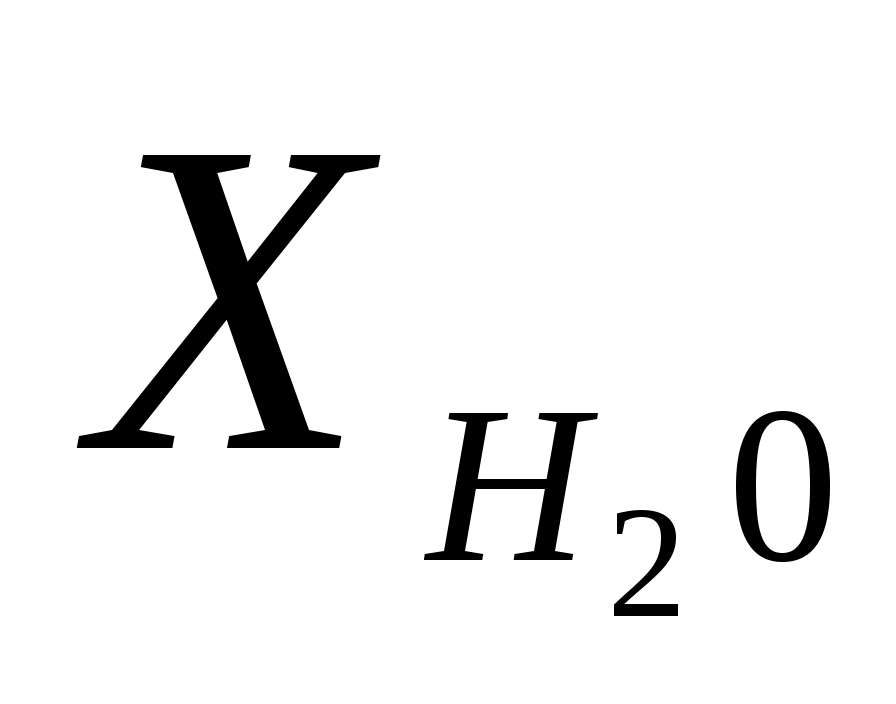 =7…9%. Причина этого – в изменении механизма цепных реакций в присутствии воды. Исследовано влияние добавок одновременно H2O и H2 на нормальную скорость горения CO в воздухе (при p=1 ата, T20oC). Получена следующая эмпирическая зависимость: =7…9%. Причина этого – в изменении механизма цепных реакций в присутствии воды. Исследовано влияние добавок одновременно H2O и H2 на нормальную скорость горения CO в воздухе (при p=1 ата, T20oC). Получена следующая эмпирическая зависимость:
 , ,
где 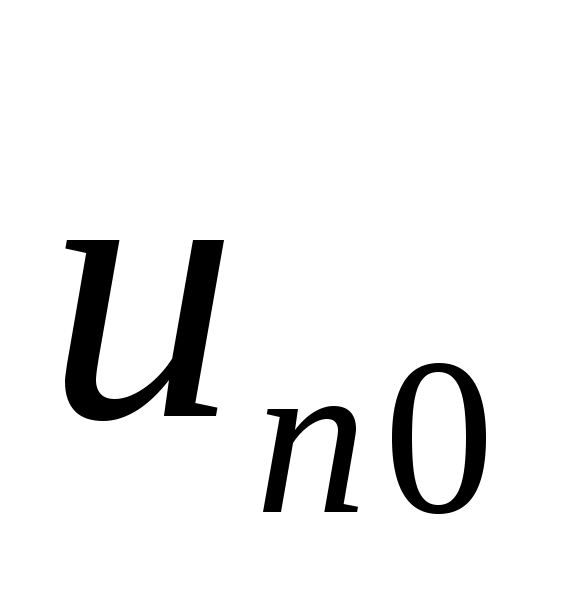 – нормальная скорость горения в отсутствие воды, – нормальная скорость горения в отсутствие воды,
 ; при ; при  =0,40…0,55 =0,40…0,55  = 14,5 см/с, = 14,5 см/с,  1400 (max), 1400 (max),
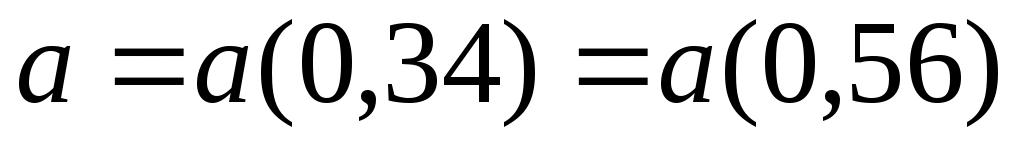  1000. 1000.
Приведенное уравнение верно для  и и 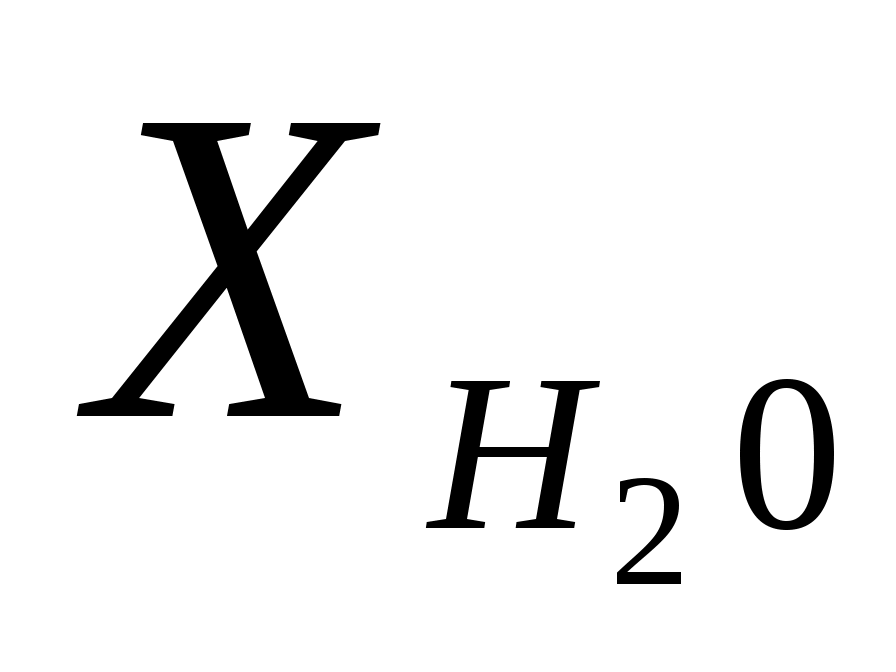 < 5…6%, при больших содержаниях влияние уменьшается. < 5…6%, при больших содержаниях влияние уменьшается.
Тот факт, что водяной пар способствует окислению CO заслуживает внимания при проектировании тепловых двигателей.
Также см. данные по влиянию H2O и NO в механизме цепных реакций (Лекция 3) и [Вильямс].
Вопросы для самоконтроля
Что такое ламинарное пламя?.
Что такое нормальная скорость горения горючей смеси?
Факторы, определяющие скорость ламинарного горения.
Закон Михельсона.
Эффект Махе.
Структура фронта ламинарного пламени.
Как получается аналитическое выражение для un в теории З., Ф.-К., С.
Как можно доказать приближенное подобие профилей YA и 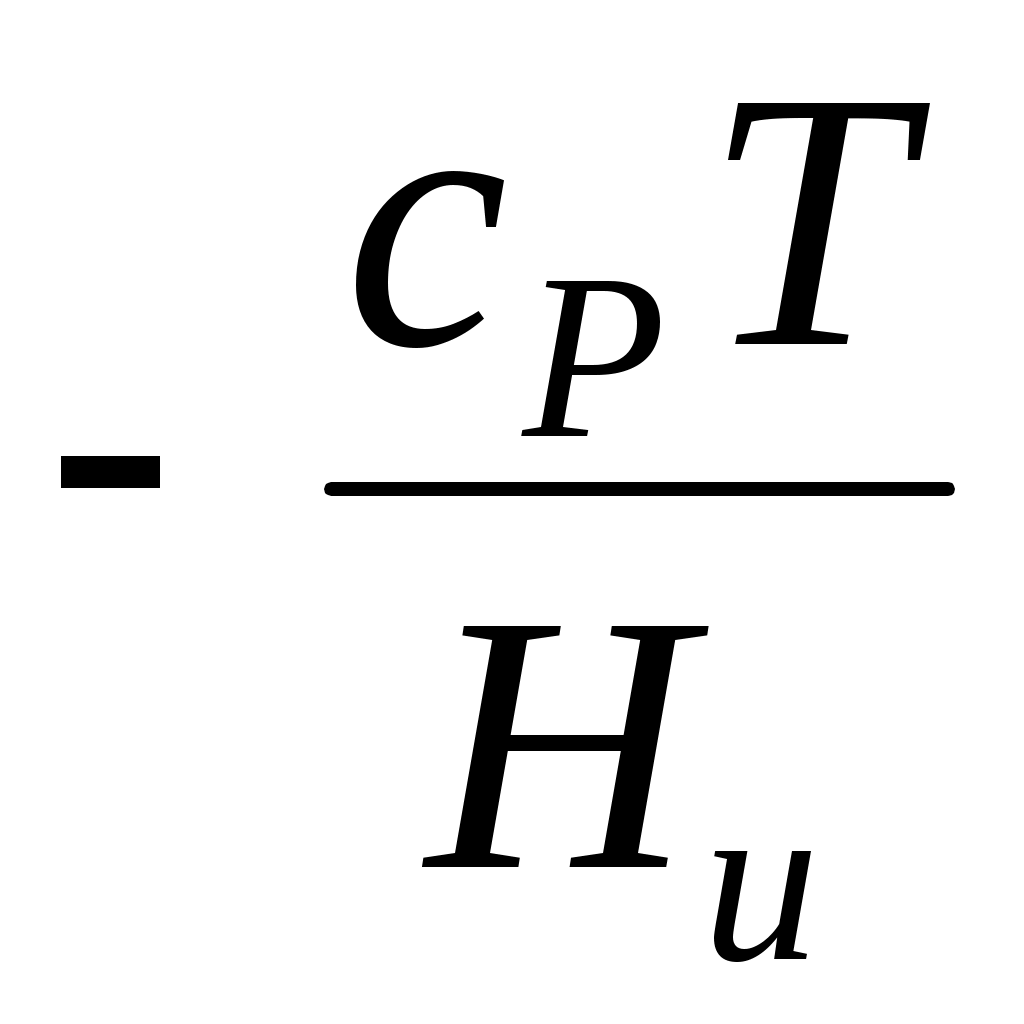 в пламени. в пламени.
9. Какие существуют методы экспериментального измерения un?
Как влияет на un начальная температура смеси?
Как влияет на un давление смеси?
Как влияет на un состав смеси: 1) при изменении; 2) при изменении относительной концентрации инертных веществ; 3) при замене одного инертного газа на другой; 4) при введении небольших добавок, влияющих на скорости реакций?
|
|
|
 Скачать 307 Kb.
Скачать 307 Kb.






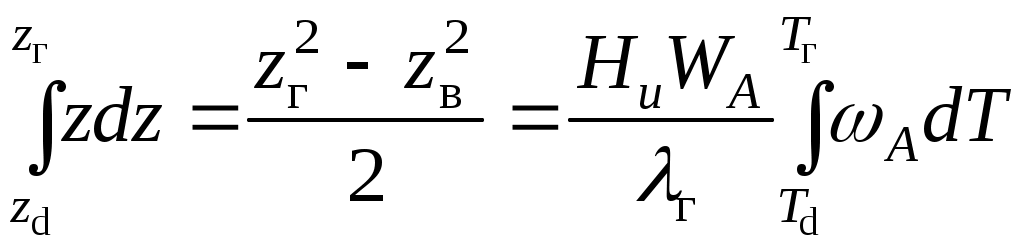 , но поскольку
, но поскольку 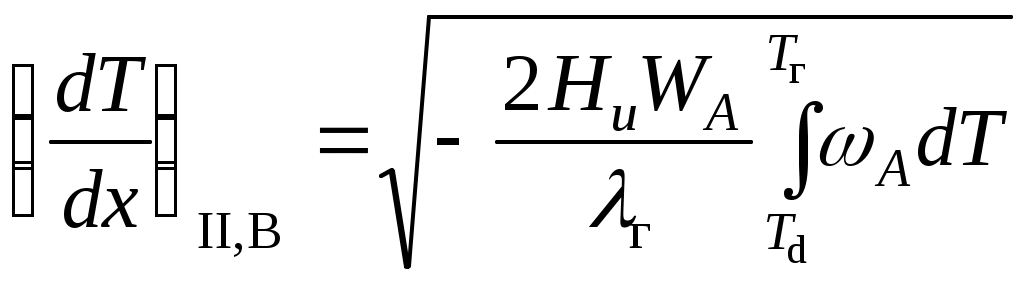 . (5.3)
. (5.3) . (5.4)
. (5.4) , (получено из (5.1))
, (получено из (5.1))
