Mathcad лабораторные работы. Отчеты_маткад_4 работы с разбивкой по пунктам. Mathcad обладает широкими возможностями численного решения уравнений и систем уравнений
 Скачать 1.35 Mb. Скачать 1.35 Mb.
|
 Ход работы: Система Mathcad обладает широкими возможностями численного решения уравнений и систем уравнений. Функция root, блоки Given…Find, Given…Minerr В ходе численного решения обычно выделяют два этапа: отделение корней – определение интервала нахождения каждого корня или определение приблизительного значения корня. В системе Mathcad наиболее наглядным будет отделение корней уравнения графическим способом; уточнение корней – нахождение численного значения корня с указанной точностью. Точность нахождения корня устанавливается с помощью системной переменной TOL (Convergence Tolerance – Допуск сходимости), которая по умолчанию равна 10-3. Чем меньше значение TOL, тем точнее, вообще говоря, находится корень уравнения. Однако оптимальным является TOL = 10-5. Переопределить значение TOL можно в окне математических свойств документа Math Options на вкладке Build-In Variables (Встроенные переменные) или присваиванием, например, TOL:=0.0001. Для решения одного уравнения с одной неизвестной предназначена встроенная функция root, которая в общем виде задается root(f(x), x, [a, b]) и возвращает значение переменной x, при котором функция f(x) обращается в ноль. Аргументы функции root: f(x) – функция левой части уравнения f(x) = 0; x – переменная, относительно которой требуется решить уравнение; a, b (необязательные) – действительные числа, такие что a < b, причем на интервале [a, b] находится только один корень. Если функция root не может найти корни уравнения, то рекомендуется уточнить начальное приближение по графику, изменить границы интервала [a, b] нахождения корня или увеличить значение системной переменной TOL. Для решения уравнений или систем нескольких уравнений и неравенств используются функции Find или Minerr. Они входят в состав вычислительного блока, который включает в себя ключевое слово Given, набор уравнений и неравенств и завершается одной из указанных вычисляющих функций в составе какого-нибудь выражения. Функция Find(x1, x2, …) возвращает значения неизвестных x1, x2, … , обращающих уравнения в верные тождества, т. е. возвращает точное решение системы уравнений или одного уравнения в частном случае. Для системы из n уравнений с n неизвестными решение возвращается в виде вектора, состоящего из n элементов. Если в результате поиска не может быть получено решение с заданной точностью, то функция Find выдает сообщение об ошибке. В этом случае можно использовать функцию Minerr(x1, x2, …), возвращающую приближенное решение системы уравнений или одного уравнения (число уравнений должно быть равно числу неизвестных). При использовании minerr необходимо производить дополнительную проверку достоверности результатов решения системы. Порядок применения блоков Given…Find, Given…Minerr для численного решения уравнений и систем уравнений: Всем неизвестным, входящим в систему, задается начальное приближение. При необходимости присваиваются требуемые значения системным переменным TOL и CTOL (Constraint Tolerance – Допуск ограничения). Печатается ключевое слово Given, которое указывает Mathcad, что далее следует система уравнений. Задаются уравнения и ограничения на поиск решения в виде неравенств (если они имеются) в любом порядке, каждое в отдельном формульном блоке, причем для записи используются операторы отношения палитры Boolean (Логические). Допускается использование двусторонних неравенств вида a ≤ x ≤ b. Применяется функция Find или Minerr в составе какого-нибудь выражения. В качестве аргументов через запятую перечисляются имена входящих в систему переменных в том порядке, в котором должны быть расположены в ответе соответствующие им корни. В случае использования функции Minerr выполняется проверка.     Метод половинного деления (метод биссектрис) В основе этого метода лежит свойство непрерывных функций, заключающееся в том, что если функция f(x) на концах отрезка [a,b] принимает значения разных знаков, т.е. f(a)∙f(b)<0, то внутри этого отрезка содержится по меньшей мере один корень уравнения f(x) = 0.  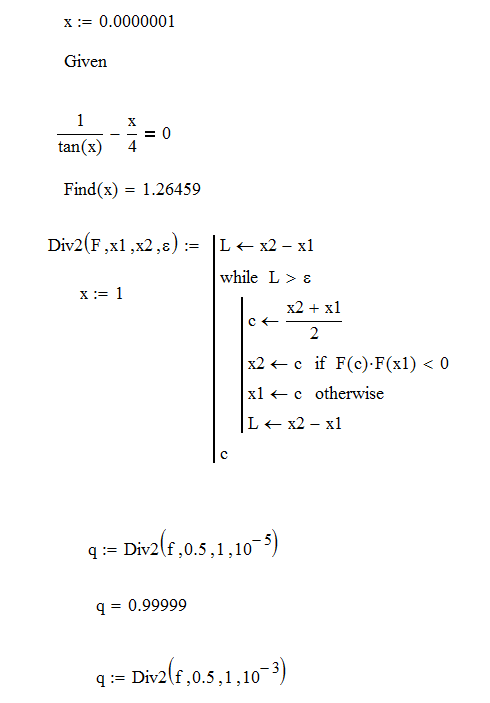 Метод Ньютона Требуется решить уравнение 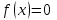 , причем , причем  и и 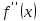 определены, непрерывны и сохраняют постоянные знаки на отрезке определены, непрерывны и сохраняют постоянные знаки на отрезке 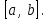 Рассмотрим геометрическую интерпретацию метода Ньютона (рис. 3.7). 1) Выбираем 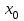 – начальное приближение корня x*. При этом надо придерживаться следующего правила: – начальное приближение корня x*. При этом надо придерживаться следующего правила: за начальное приближение корня следует принять тот конец отрезка 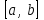 , в котором знак функции совпадает со знаком второй производной, т.е. выполняется условие: , в котором знак функции совпадает со знаком второй производной, т.е. выполняется условие: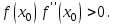 (3.23) (3.23)Это условие сходимости метода Ньютона. 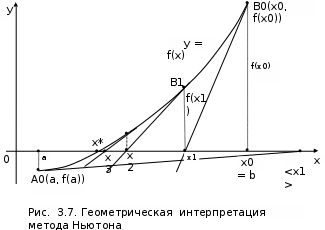 Основываясь на свойствах данной функции f(x) (см. рис. 3.4), делаем вывод: условие сходимости выполняется для точки 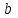 , поэтому принимаем , поэтому принимаем 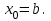 2) Вычисляем значение функции 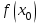 . Проводим касательную к кривой . Проводим касательную к кривой  в точке в точке 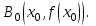 . Абсцисса точки пересечения касательной с осью Оx принимается за новое (первое) приближение корня x1. . Абсцисса точки пересечения касательной с осью Оx принимается за новое (первое) приближение корня x1. Известно, что уравнение касательной, проведенной в точке B0 с координатами (x0, f(x0)) к кривой функции f(x), имеет вид: 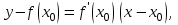 (3.24) (3.24)где x, y – текущие координаты точки, лежащей на касательной. Для точки x1 сделаем подстановку в уравнение касательной (3.24): x = x1; (3.25) 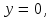 (3.26) (3.26)получаем: 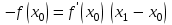 . (3.27) . (3.27)Обе части уравнения (3.27) делим на  и выражаем x1: и выражаем x1: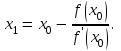 (3.28) (3.28)3) Вычисляем значение функции  в точке x1, проводим касательную к кривой в точке x1, проводим касательную к кривой  в точке в точке 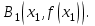 Абсцисса точки пересечения касательной с осью Оx представляет собой второе приближение корня x2: Абсцисса точки пересечения касательной с осью Оx представляет собой второе приближение корня x2: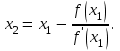 (3.29) (3.29) 4) Продолжаем последовательно проводить касательные и определять точки их пересечения с осью Оx. Тогда для текущего k-го приближения корня итерационный процесс реализуется рекуррентной формулой: 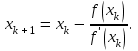 (3.30) (3.30)Процесс уточнения корня прекращается, когда выполнится условие близости двух последовательных приближений: 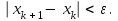 (3.31) (3.31) Алгоритм, реализующий метод Ньютона, представлен на рис. 3.8. Блок 4 реализует проверку условия сходимости метода и выбор значения начального приближения (блоки 5, 6). Блок 10 реализует подсчет количества итераций, 11 – вычисление текущего приближения корня через предыдущее приближение. Метод Ньютона обладает высокой скоростью сходимости, которая тем выше, чем больше крутизна графика функции  в пределах рассматриваемого отрезка. Если численное значение производной в пределах рассматриваемого отрезка. Если численное значение производной 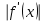 мало вблизи корня, то процесс уточнения корня может оказаться очень долгим. мало вблизи корня, то процесс уточнения корня может оказаться очень долгим.Неудачно выбранное начальное приближение может привести к расходимости метода (см. рис. 3.7): представим, что за начальное приближение x0 принят левый конец отрезка a, касательная, проведенная в точке А0, пересекает ось Оx за пределами заданного отрезка [a,b]. Таким образом, получили первое приближение к корню ‹x1›, еще дальше отстоящее от искомого значения корня x*, чем нулевое приближение 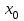 . .Реализация метода Ньютона в Mathcad Для алгебраического уравнения   Для трансцендентного уравнения п. 2-6 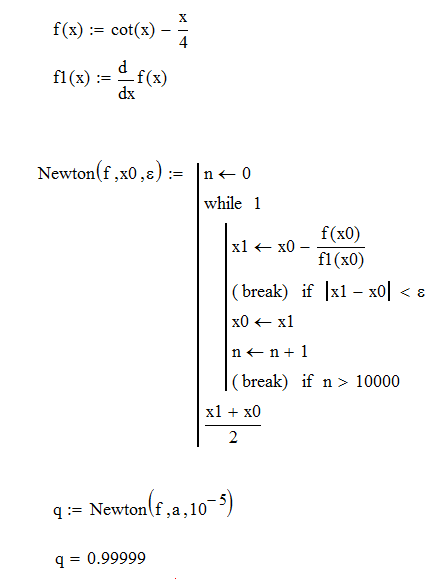 8* Метод простой итерации В методе простой итерации исходное уравнение f(x)=0 представляется в эквивалентном виде φ(x)=x (что, вообще говоря, можно сделать бесконечным числом способов), а затем шаг метода выполняется по формуле xk+1 = φ(xk), пока не будет достигнута заданная точность |xk+1-xk|<ε. Если выбрать φ(x)=x-c*f(x), то константу c целесообразнее всего искать методом релаксации, для которого c=2/(M+m), где M - максимальное из значений первой производной на концах отрезка или в находящихся на нём точках перегиба функции (точках, где f''(x)=0), а m - минимальное из таких значений. Вот соответствующий расчёт в MathCAD: Для трансцендентного уравнения    Лабораторная работа №1. Погрешность результата численного решения Цель: Получить навыки исследования погрешности численного решения. Освоить методы подсчета погрешностей заданной функции по известным погрешностям входящих в нее параметров.  Содержание работы Содержание работы1. Вычислить значение аналитического выражения (варианты заданий Таблица 1.1) и оценить абсолютную и относительную погрешности сложной функции. 2. По полученным в пункте 1. относительной или абсолютной погрешности аналитического выражения округлить сомнительные цифры числа (аналитического выражения), оставив только верные знаки. 3*. Определить какое равенство точнее (варианты заданий Таблица 1.2).  Ход работы:     Лабораторная работа №1 Приближенное вычисление определенного интеграла на основе квадратурных формул Цель работы: Освоить методы приближенного вычисления определенного интеграла с заданной точностью на основе квадратурных формул.   Ход работы: Построим график заданной функции:  Вычислим в системе MathCAD значения неопределенного и определенного интеграла для функций f x ( ) в символьном и численном виде  Вычислить приближенное значение интеграла по формуле трапеции 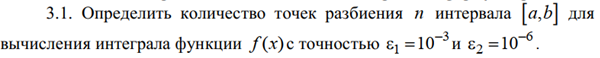 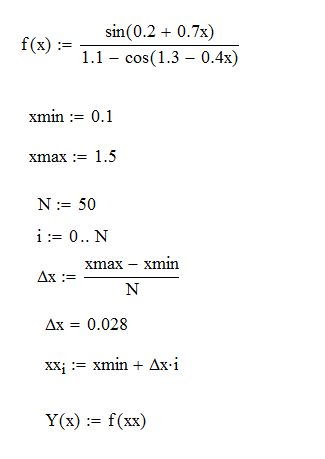 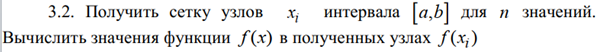   3.3 Программа вычисления интеграла методом трапеций 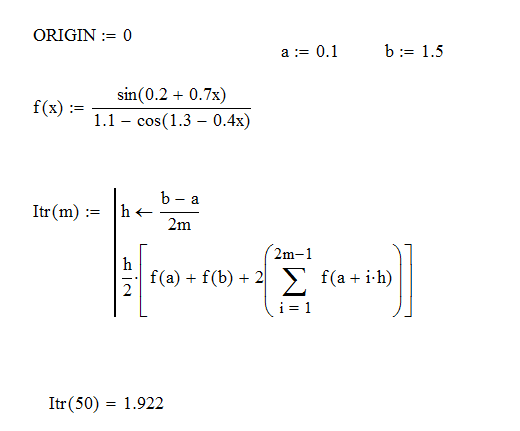   5. Вычислим интеграл по формуле Симпсона для функции y (x).  ИСПОЛЬЗОВАНИЕ МОДУЛЬНОГО ПРОГРАММИРОВАНИЯ СКМ MathCAD В ЗАДАЧАХ ОПТИМИЗАЦИИ ЦЕЛЬ РАБОТЫ: Получить навыки программирования пользовательских задач в СКМ ППП MathCAD СОДЕРЖАНИЕ РАБОТЫ Вариант 11   Ход работы: Для выбранного варианта задания (Таблица 1) построить в одних числовых осях графики функции f(x) и f'(x) для заданного диапазона изменения аргумента [a, b]. Графики должны сдержать числовые оси, линии сетки, подпись графика.  2.        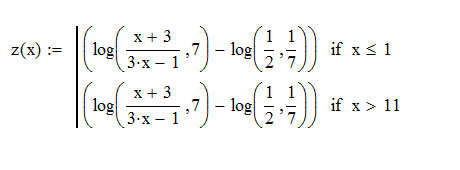   |
