Матричные игры двух лиц с нулевой суммой. Матричные игры двух лиц с нулевой суммой

• Название: Матричные игры двух лиц с нулевой суммой
• Дата: 18.12.2021
• Размер: 130 Kb.
• Имя файла: Матричные игры двух лиц с нулевой суммой.doc
• Тип: Исследование; #307699

Министерство Образования Российской Федерации

Уфимский Государственный Авиационный Технический Университет


Отчет по лабораторной работе №4

предмет «Системный анализ и исследование операций»

на тему: «Матричные игры двух лиц с нулевой суммой»

Выполнили:

студенты гр. АСОИ-335:
Проверил: Бабак С.Ф.


Уфа 2010

Цель работы: изучение упрощения платежных матриц, свод матрицы к парам двойственных задач ЛП и нахождение цены игры ,а так же оптимальных векторов с помощью графического и симплекс методов.
Задача №1
Сделать возможные упрощения платежной матрицы

	В1	В2	В3	В4	В5	В6
А1	7	9	7	5	6	12
А2	9	10	6	5	8	9
А3	8	-5	2	3	1	4

3-я строка доминирует над 2-й, опускаем третью строку:

	В1	В2	В3	В4	В5	В6
А1	7	9	7	5	6	12
А2	9	10	6	5	8	9

2-й столбец доминирует над 1-м, 3-м, 4-м и 5-м столбцами, опускаем второй столбец:

	В1	В3	В4	В5	В6
А1	7	7	5	6	12
А2	9	6	5	8	9

6-й столбец доминирует над оставшимися столбцами, опускаем 6-й столбец:

	В1	В3	В4	В5
А1	7	7	5	6
А2	9	6	5	8

1-й столбец доминирует над 5-м, опускаем 1-й столбец:

	В3	В4	В5
А1	7	5	6
А2	6	5	8

5-й столбец доминирует над 4-м столбцом, опускаем 5-й столбец:

	В3	В4
А1	7	5
А2	6	5

3-й столбец доминирует над 4-м, опускаем 3-й столбец:

	В4
А1	5
А2	5

Отсюда видно, что наилучшей стратегией игрока А являются чистые стратегии А1 и А2, обеспечивающие ему наибольший выигрыш, равный 5, а для игрока В – чистая стратегия В4, обеспечивающая минимальным проигрыш равный 5. В данном примере в результате упрощения платежной матрицы удалось найти решение игры в чистых стратегиях. Объясняется это тем, что данная платежная матрица обладает седловыми элементами a₁₄=5 и a₂₄=5, в чем легко убедиться, проанализировав платежную матрицу в исходной записи.

Задача №2
Свести к парам двойственных задач ЛП

	В1	В2	В3
А1	-4	-8	-4
А2	-6	0	0
А3	-5	-5	0

Проверим матрицу на наличие седловой точки:
α=max min a_ij =-5

β=min max a_ij =-4

α ≠ β
3-й столбец доминирует над 1-м и 2-м, опускаем 3-й столбец:

	В1	В2
А1	-4	-8
А2	-6	0
А3	-5	-5

Решаем с помощью ПЭР(пакет экономических расчетов).
y1+y2max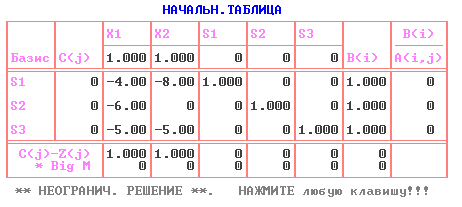


x1+x2+x3min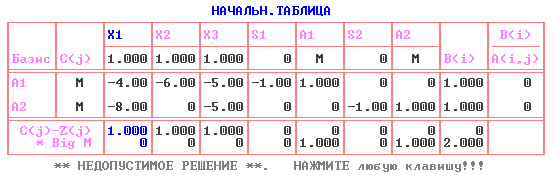



Задача №3
Произвести упрощения и решить графическим методом

	В1	В2	В3	В4	В5
А1	5	2	0	3	4
А2	1	4	6	2	5
А3	0	4	3	1	2

3-я строка доминирует 2-ю, опускаем 3-ю строку:

	В1	В2	В3	В4	В5
А1	5	2	0	3	4
А2	1	4	6	2	5

5-й столбец доминирует 2-й и 4-й столбец, опускаем 5-й столбец:

	В1	В2	В3	В4
А1	5	2	0	3
А2	1	4	6	2

1-й и 2-й столбец доминируют над 4-м, опустим эти столбцы:

	В3	В4
А1	0	3
А2	6	2

α=max min a_ij =0

β=min max a_ij =5

α ≠ β => седловой точки нет.
Сводим матричную игру к задаче ЛП:

x1+x2max

3x2≤1 (1)

6x1+2x2≤1 (2)

x1≥0; x2≥0;

Решаем геометрическим (графическим) методом:
Формулируем двойственную задачу:

x1	x2
1	1
0	3	1	y1
6	2	1	y2

y1+y2min




6y2≥1 (1)

3y1+2y2≥1 (2)

y1≥0; y2≥0;
Ищем значения по правилу согласования:

(6y2-1)x1=0;

(3y1+2y2-1)x2=0;

(3x2-1)y1=0;

(6x1+2x2-1)xy=0;


Задача №4.1
Предприятие выпускает скоропортящуюся продукцию, которую оно может сразу отправить потребителю (стратегия А), отправить на склад для хранения (стратегия Б), или подвергнуть дополнительной обработке (стратегия В) для длительного хранения.

В свою очередь потребитель может немедленно приобрести эту продукцию(стратегия 1), приобрести ее в течении небольшого отрезка времени(2) или затребовать ее после длительного периода времени (3).

Если предприятие выберет стратегию А, то дополнительные затраты на хранение и обработку продукции не потребуется.

Однако, если при этом потребитель применит стратегию 2 или тем более 3, то предприятие потерпит убытки, из-за порчи части продукции. Наоборот, если предприятие выберет стратегию В. А потребитель – стратегию 1, то возникнут неоправданные расходы на консервацию продукции. Определите оптимальное соотношение между продукцией, отправляемой потребителю на склад и на дополнительную обработку, руководствуясь «минимаксным критерием» (гарантированный средний уровень убытка).

	A	B	C
1	2	5	8
2	7	6	10
3	12	10	8

Проверяем матрицу на наличие седловой точки:

α=max min a_ij =8

β=min max a_ij =10

α ≠ β => седловой точки нет.
Решаем с помощью ПЭР (пакет экономических расчетов).

x1+x2+x3min

x1=0; x2=0,0385; x3=0,0769; φ_min=0,1153846

Получаем:

Цена игры – v=1/φ_min =8,67.

Компоненты оптимальной смешанной стратегии:

p1=0;

p2=v*x2=0,3338;

p3=v*x3=0,6667;
Мы определили оптимальное соотношение между продукцией, отправляемой потребителю на склад и на дополнительную обработку, руководствуясь «минимаксным критерием» (гарантированный средний уровень убытка).

Задача №4.2
Для отопления помещения необходимо приобрести топливо. Однако расход топлива и цены на него зависят от погоды в зимнее время (мягкая, нормальная и суровая зима; см. таблицу)

Погода	Мягкая	Нормальная	Суровая
Расход, т.	5	10	18
Цена, руб./т.	10	16	20

В настоящее время уголь может быть приобретен по минимальной цене (10 руб./т.) и излишек неиспользованного угля можно реализовать весной по цене 5 руб./т. Можно избрать одну из трех стратегий в закупке угля: А₁ ­– 5 т., А₂ – 10 т. и А₃ – 18 т.

Предполагая, что подобных помещений имеется 100, определить оптимальную стратегию в образовании запасов, руководствуясь «минимаксным критерием».

Стратегия А₁ (полагаем, что зима будет мягкой):
Затраты на покупку: 5 т. ∙ 100 ∙ 10 руб./т. = 5000 руб.
Дополнительные затраты:
Вариант 1

Топлива достаточно (зима мягкая):

доп. затраты = 0

Вариант 2

Нехватка 500 т. (зима нормальная):

доп.затраты = 5 т. ∙ 100 ∙ 16 руб./т. = 8000 руб

Вариант 3

Нехватка 1300 т. (зима суровая):

доп. затраты = 13 т. ∙ 100 ∙ 20 руб./т. = 26000 руб.

Стратегия А₂ (полагаем, что зима будет нормальной):
Затраты на покупку: 10 т. ∙ 100 ∙ 10 руб./т. = 10000 руб.
Дополнительные затраты:
Вариант 1

Избыток топлива в 500 т. (зима мягкая):

доп. затраты = -5 т. ∙ 100 ∙ 5 руб./т. = -2500 руб.

Вариант 2

Топлива достаточно (зима нормальная):

доп.затраты = 0

Вариант 3

Нехватка 800 т. (зима суровая):

доп. затраты = 8 т. ∙ 100 ∙ 20 руб./т. = 16000 руб.

Стратегия А₃(полагаем, что зима будет суровой):
Затраты на покупку: 18 т. ∙ 100 ∙ 10 руб./т. = 18000 руб.
Дополнительные затраты:
Вариант 1

Избыток топлива в 1300 т. (зима мягкая):

доп. затраты = -13 т. ∙ 100 ∙ 5 руб./т. = -6500 руб.

Вариант 2

Избыток топлива в 800 т. (зима нормальная):

доп.затраты = -8 т. ∙ 100 ∙ 5 руб./т. = -4000 руб.

Вариант 3

Топлива достаточно (зима суровая):

доп. затраты = 0
Составим матрицу расходов с учетом дополнительных затрат:

	А1	А2	А3
мягкая	5000	7500	11500
нормальная	13000	10000	14000
суровая	31000	26000	18000

α=max min a_ij =18000

β=min max a_ij =18000

α = β, т.е. оптимальной стратегией является стратегия А₃: закупка 1800 т. угля по цене 10 руб./т.


Задача №4.3
Магазин может завести в различных пропорциях товары трех типов (А, Б и В). Их реализация, а следовательно, и получаемая прибыль (a­_ik) зависят от вида товара и состояния спроса. Предполагая, что последний может характеризоваться тремя состояниями (I, II, III) и учитывая, что спрос связан с изменением моды и прогнозирование его невозможно, определить оптимальные пропорции в закупке товаров из условия средней гарантированной прибыли при следующей матрице прибылей:

	I	II	III
А	20	15	10
Б	16	12	14
В	13	18	15

α=max min a_ij =13

β=min max a_ij =15
α ≠ β => седловой точки нет.
Решаем с помощью ПЭР (пакет экономических расчетов).

x1+x2+x3max

x1=0;
x1=0,0172, x2=0; x3=0,0517; φ_min=0,06896552

Получаем:

Цена игры – v=1/φ_min =14,499.

Компоненты оптимальной смешанной стратегии:

p1=v*x1= 0,2494;

p2=0;

p3=v*x3= 0,7496;

Мы определили оптимальное соотношение между закупкой товаров типа А и В, руководствуясь «максиминным критерием» (средняя гарантированная прибыль).

Вывод: в данной лабораторной работе были рассмотрены принципы упрощения платежных матриц, свод матрицы к парам двойственных задач ЛП и нахождение цены игры, а так же оптимальных векторов с помощью графического и симплекс методов.