Механические испытания. Л2.МЕХАНИЧЕСКИЕ ИСПЫТАНИЯ. Механические испытания материалов 1 Краткие сведения о некоторых конструкционных материалах Сталь
 Скачать 0.68 Mb. Скачать 0.68 Mb.
|
|
Механические испытания материалов 1.1 Краткие сведения о некоторых конструкционных материалах Сталь – сплав железа с углеродом (до 2,14 %). По химическому составу различают углеродистые и легированные стали. Углеродистые стали вместе с железом и углеродом содержат марганец (до 1 %) и кремний (до 0,4%), а также некоторые примеси (сера и фосфор). По содержанию углерода стали делятся на низкоуглеродистые, среднеуглеродистые и высокоуглеродистые. В состав легированных сталей, помимо указанных компонентов, входят легирующие элементы (хром, никель, молибден, вольфрам и др.), которые повышают качество стали и придают ей особые свойства. Сплав железа с углеродом, содержание которого выше 2,14 % называют чугуном. Алюминиевые сплавы (силумины, дюралюмины) – сплавы на основе алюминия с добавлением меди, магния, цинка, марганца и других элементов. Обладают высокими механическими свойствами, малой плотностью, высокой электро- и теплопроводностью, хорошей коррозионной стойкостью. Бетон – искусственный каменный строительный материал, получаемый в результате формования и затвердевания рационально подобранной и уплотнённой смеси, состоящей из вяжущего вещества (цемента), крупных заполнителей (щебень, гравий), мелких заполнителей (песок), воды. Древесина – важнейший строительный материал. В строительстве широко используют сосну, ель, дуб, лиственницу; различные древесноволокнистые и древесностружечные плиты и т.п. Композитные материалы, как правило, имеют армирующие элементы в виде нитей, волокон, металлической арматуры. Например, пластик, армированный борными, стеклянными или углеродистыми волокнами; алюминий, армированный борными или стальными нитями; железобетонные изделия и т.п. Комбинируя объёмное содержание компонентов, можно получить композиционные материалы с требуемыми физико-механическими свойствами. 1.2 Испытания материалов на растяжение Основные прочностные и деформационные характеристики материалов определяют экспериментально. Испытаниям подвергают стандартные лабораторные образцы на различные воздействия: растяжение, сжатие, сдвиг, кручение, изгиб. Испытания проводятся на лабораторных установках – разрывных машинах, прессах при статическом или динамическом нагружении, на воздухе (нормальные условия) и в агрессивных средах, при комнатной, высоких и низких температурах. Наиболее простым и распространенным является испытание на растяжение статической нагрузкой, позволяющей определить большинство механических характеристик. Испытания на растяжение проводятся на образцах, которые вытачиваются из прутковых заготовок или вырезаются из листа. Основной особенностью таких образцов является наличие усиленных мест захвата и плавного перехода к сравнительно узкой ослабленной рабочей части. Для цилиндрического образца (рис. 1.1) расчëтная длина l0 принимается равной 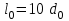 или или 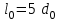 . Первые называют десятикратными или условно «длинными», а вторые – пятикратными или условно «короткими». Стандарт предусматривает несколько типов образцов, диаметр которых может изменяться в пределах от 3 до 25 мм. . Первые называют десятикратными или условно «длинными», а вторые – пятикратными или условно «короткими». Стандарт предусматривает несколько типов образцов, диаметр которых может изменяться в пределах от 3 до 25 мм. 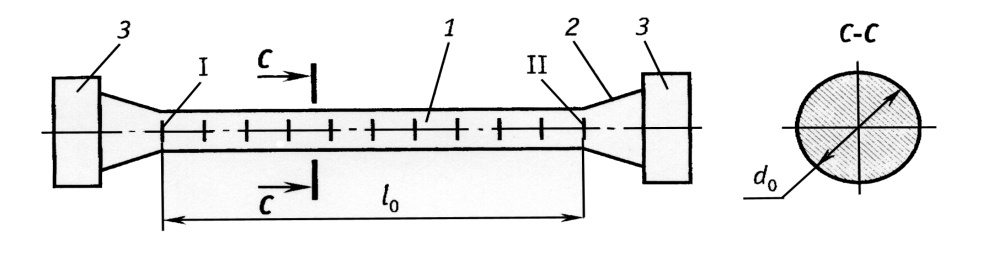 Рис. 1.1. Стандартный образец круглого сечения: 1 – рабочая часть образца (от риски I до риски II); 2 – переходные части; 3 – утолщëнные головки Для испытаний листового материала используют прямоугольные образцы (рис. 1.2), ширина которых 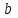 в три раза больше толщины в три раза больше толщины 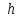 . .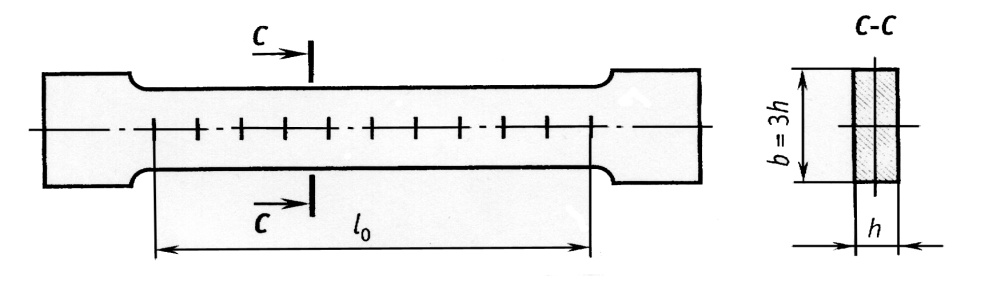 Рис. 1.2 Расчëтная длина рабочей части плоского образца определяется соотношениями: 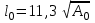 (десятикратный образец); (десятикратный образец);  (пятикратный образец), где (пятикратный образец), где  – площадь сечения рабочей части. – площадь сечения рабочей части.В процессе испытания образца на разрыв диаграммный аппарат испытательной машины вычерчивает диаграмму растяжения в осях 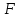 (нагрузка) – (нагрузка) –  (удлинение). (удлинение). Для определения механических характеристик материала диаграмму 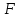 – – перестраивают в осях σ – ε (напряжения – деформации) по формулам: перестраивают в осях σ – ε (напряжения – деформации) по формулам:  , ,  . .Примерный вид диаграммы σ – ε для пластичного материала (низкоуглеродистой стали типа ВСт3) показан на рис. 1.3. 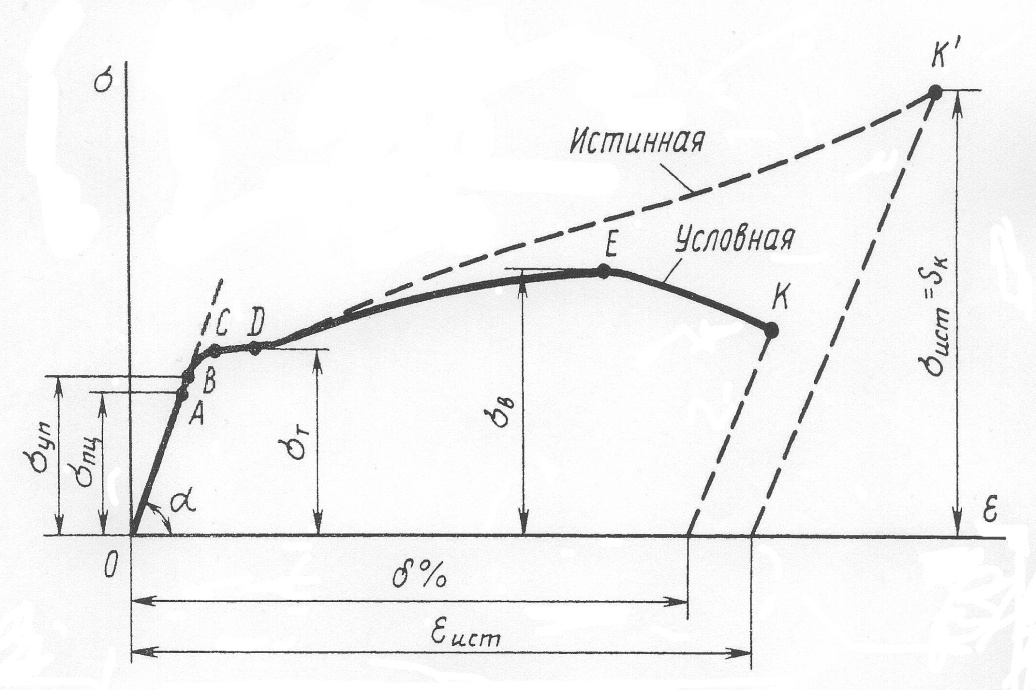 Рис. 1.3. На диаграмме растяжения выделяют характерные точки и участки. Участок ОА – зона пропорциональности. Здесь зависимость между и нагрузкой и удлинением образца является линейной, что подтверждает справедливость действия закона Гука. Наибольшее напряжение, до которого соблюдается закон Гука, называется пределом пропорциональности σпц (y). Для стали ВСт3 σпц = 195 – 200 МПа. Если в любой точке на этом участке сбросить нагрузку до нуля, то график разгрузки совпадет с графиком нагружения, т.е. при напряжениях 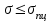 возникают только упругие деформации. возникают только упругие деформации. По углу наклона прямой ОА можно определить значение модуля упругости E (модуля Юнга) материала:  . .Следует отметить, что величина модуля упругости E практически не зависит от химического состава и термической обработки стали. При дальнейшем нагружении образца от точки А до точки В линейная зависимость нарушается, но при разгрузке образца возникшие деформации исчезают, т.е. материал остается упругим. Наибольшее напряжение, при котором в материале при разгрузке не возникают остаточные деформации, называется пределом упругости σуп (e). Предел упругости характеризует начало перехода от упругой деформации к пластической (остаточной). Для стали ВСт3 σуп= 205 – 210 МПа, т.е. σпц и σупотличаются незначительно, и обычно считают, что они совпадают. В дальнейшем не будем делать между ними различия и ограничимся рассмотрением только предела пропорциональности, как практически более важной величины. При дальнейшем нагружении криволинейная часть диаграммы переходит в почти горизонтальный участок СD – зону текучести. Здесь деформации растут практически без увеличения нагрузки: материал так бы уподобляется жидкости и "течёт". Физическим пределом текучести σТ называется наименьшее напряжение, при котором образец деформируется без заметного увеличения нагрузки. Для стали ВСт3 σТ = 220 – 250 МПа. Если необходимо отличить предел текучести на растяжение от предела текучести на сжатие, то в обозначение вводится дополнительный индекс "p" или "с" – соответствующий растяжению (σТ.Р) или сжатию (σТ.С). Диаграммы растяжения некоторых пластичных материалов и сплавов (среднеуглеродистая сталь, медь, алюминий, дюрали и др.), а также хрупких материалов (легированная сталь, ковкий чугун и др.) не имеют площадки текучести. Для них вводится понятие условного предела текучести 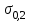 – представляющего собой напряжение, при котором относительное остаточное удлинение образца равно 0,2%. – представляющего собой напряжение, при котором относительное остаточное удлинение образца равно 0,2%. Зона BD называется зоной общей текучести. В этой зоне значительно развиваются пластические (остаточные) деформации, несколько повышается температура образца, изменяются электропроводность и магнитные свойства материала образца. При текучести стали отшлифованная блестящая поверхность образца становится матовой и не ней можно обнаружить появление линий, наклоненных к оси образца приблизительно под углом 45º, называемых линиями Людерса-Чернова (рис. 1.4). Эти линии представляют собой микроскопические неровности, возникающие вследствие необратимых сдвигов, происходящих в кристаллах под действием наибольших касательных напряжений. Описанные явления вызывают изменение структуры металла, что приводит к его упрочнению.   Рис. 1.4. Участок DЕ – зона упрочнения. Диаграмма после зоны текучести становится криволинейной. При увеличении нагрузки в зоне упрочнения в образце появляется местное сужение – образуется так называемая шейка (рис.1.5). 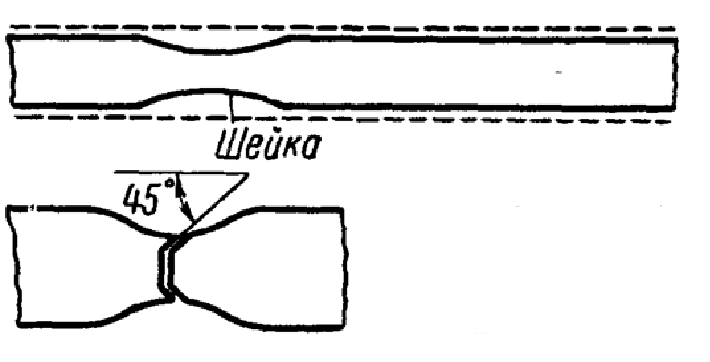 Рис.1.5 Отношение наибольшей силы Fmax, которую способен выдержать образец, к первоначальной площади поперечного сечения образца называется временным сопротивлением или условным пределом прочности в(u): 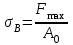 . . Строго говоря, понятия «временное сопротивление» и «предел прочности» не совсем тождественны. Первое из них относится к пластичным материалам, на образцах из которых перед разрушением образуется шейка. Второе относится к случаю, когда образец разрушается без образования шейки, что характерно для хрупких материалов. Для стали ВСт3 σВ = 370 – 470 МПа. В отечественной технической литературе можно встретить обозначения 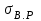 и и  , определенные при растяжении и сжатии. , определенные при растяжении и сжатии.Участок EK – зона местной текучести. Разрыв образца происходит в пределах шейки. При этом нагрузка Fпадает (точка К, рис.1.3), хотя истинное значение напряжения при разрыве в связи с резким уменьшением площади поперечного сечения возрастает (точка К′).  Рис.1.6 Образец разрушается с образованием чашечки (кратера) на одной его части и выступа на другой. На дне чашечки, разрушение имеет характер отрыва в результате действия нормальных напряжений. Края же разрушаются вследствие сдвига в направлении наибольших касательных напряжений под углом около 45º (рис. 1.6). Такое разрушение называют вязким (пластичным). Диаграмма, показанная на рис. 1.3 сплошной жирной линией называется условной, т.к. при её построении не учитывается изменение площади поперечного сечения образца в процессе испытания. Диаграмма, показанная пунктирной линией, построенная с учётом сужения образца, называется истинной (действительной) диаграммой напряжений. Напряжение, соответствующее точке K′, называют истинным сопротивление разрыву (истинным пределом прочности). Для стали ВСт3 истинное сопротивление разрыву достигает 900 – 1000 МПа. Необходимо отметить, что в реальных конструкциях напряжения не должны превосходить предел текучести материала σТ. Поэтому истинная диаграмма растяжения, как правило, не имеет практического применения. Рассмотренные выше напряжения: предел пропорциональности σпц, предел текучести σТ, предел прочности σВ называются механическими характеристиками прочности материала и относятся к первой группе механических характеристик. По результатам испытаний образца после разрыва можно определить механические характеристики пластичности материала (вторая группа механических характеристик). К ним относят: 1) Относительное остаточное удлинение при разрыве δ – отношение приращения расчетной длины образца (l1 – l0) при разрыве к начальной расчетной длине 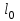 , выраженное в процентах , выраженное в процентах  . .Следует отметить, что для одного и того же материала, значение  различно, в зависимости от отношения расчëтной длины образца различно, в зависимости от отношения расчëтной длины образца 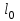 к его диаметру к его диаметру 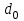 , при испытании которого она получена. Полученное при испытании «длинных» образцов , при испытании которого она получена. Полученное при испытании «длинных» образцов 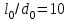 значение относительного остаточного удлинения при разрыве обозначают значение относительного остаточного удлинения при разрыве обозначают  , а в случае «коротких» , а в случае «коротких»  – – 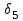 . При этом для данного материала всегда . При этом для данного материала всегда 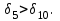 2) Относительное остаточное сужение при разрыве ψ – изменение площади сечения образца до деформации и после разрыва (А0 – А1), отнесённое к начальной площади поперечного сечения образца А0, выраженное в процентах: 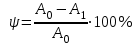 . .Чем пластичнее материал, тем больше относительное удлинение и относительное сужение при разрыве. Материалы условно подразделяют на пластичные  и хрупкие и хрупкие 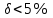 . Для рассматриваемой стали ВСт3 . Для рассматриваемой стали ВСт3 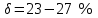 , ,  . . Необходимо также понимать, что полное удлинение, полученное образцом непосредственно перед разрушением, является результатом упругой деформации и пластической деформации. После разрыва растягивающая сила, а следовательно, и упругая деформация, обращаются в нуль. Таким образом, длина образца после разрыва l1 будет равна: l1=l0+Δlост, где Δlост – остаточное (пластическое) удлинение, l0 – первоначальная длина. Идеальная диаграмма Прандтля При выполнении практических расчётов диаграмму напряжений упрощают, применяя аппроксимирующие диаграммы. Удобно применять идеальную диаграмму Прандтля (рис.1.7).  Рис. 1.7 Считая, что предел пропорциональности, предел упругости и предел текучести имеют близкие значения, диаграмму схематизируют в виде двух прямых, полагая, что все три указанных напряжения соответствуют одной точке – σТ. Диаграмма Прандтля отражает одну из характерных особенностей поведения упруго-пластического материала – способность к большим пластическим деформациям. Наклеп На стадии упрочнения (участок DE на рис. 1.8) материал деформируется упруго-пластически. 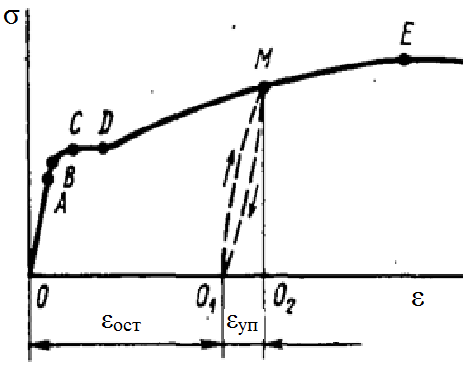 Рис. 1.8 Если из некоторой точки M, лежащей выше предела упругости, произвести разгрузку, то график пойдет по линии МО1, практически параллельной участку ОВ. Упругая деформация εуп = О1О2, как отмечалось выше, исчезает после снятия нагрузки. Отрезок ОО1 = εост представляет собой остаточную деформацию. Таким образом, за пределом упругости полная деформация, соответствующая точке M на диаграмме, состоит из двух частей – упругой и пластической: ε = εост + εуп. Если нагрузить образец вновь, то диаграмма пойдет по прямой О1М практически совпадающей с линией разгрузки МО1, и дальше пойдет по кривой ME. Участок диаграммы МО1М называется петлей гистерезиса. Изучая диаграмму повторного нагружения О1МE, можно сделать следующие выводы: исчезла площадка текучести; предел пропорциональности повысился и стал равным напряжению, до которого первоначально был растянут образец (точка M); уменьшилась деформация после разрыва на величину εуп, т.е. диаграмма оказалась укороченной, и материал стал как бы менее пластичным и более хрупким. Явление повышения упругих свойств материала полученное в результате предварительной пластической обработки материала с последующей разгрузкой называется наклёпом(нагартовкой). Таким образом, при наклёпе повышаются упругие свойства и понижается пластичность. В некоторых случаях (например, при механической обработке) явление наклепа нежелательно и его устраняют термообработкой (отжиг) или удалением наклепанного слоя. В других случаях его создают искусственно для улучшения упругости деталей или конструкций (обработка дробью или вытяжка цепей, тросов и канатов грузоподъемных машин, некоторые виды арматуры железобетонных конструкций). Диаграммы растяжения других материалов Многие материалы имеют диаграмму растяжения, существенно отличающуюся от приведенной выше диаграммы для стали ВСт3. На рис.1.9 показана диаграмма для низколегированной стали. Аналогичный вид имеют диаграммы сплавов алюминия.  Рис. 1.9. На этой диаграмме растяжения нет площадки текучести. Поэтому вместо физического предела текучести определяют условный предел текучести 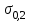 . . Участок диаграммы EK у низколегированной стали короче, чем аналогичный участок у низкоуглеродистой стали. Это указывает на то, что низколегированная сталь обладает меньшей пластичностью, поэтому шейка у нее является менее выраженной. Механические характеристики прочности низколегированной стали выше, чем у низкоуглеродистой стали. Диаграмма растяжения чугуна, представленная на рис. 1.10, является типичной для хрупких материалов.  Рис. 1.10. Отличительной особенностью таких материалов является то, что они не подчиняются закону Гука (диаграмма не имеет прямолинейного участка), в них не наблюдается текучесть. Образец разрушается при весьма малых удлинениях и без образования шейки. Остаточные деформации очень малы, обычно менее 1% от расчетной длины образца. Разрушение чугунного образца происходит в результате отрыва по площадке, перпендикулярной направлению растягивающей силы. На поверхности излома видна крупнозернистая структура. Хрупкие материалы плохо сопротивляются растяжению. 1.3 Потенциальная энергия деформации. Удельная работа разрушения Внешние силы, приложенные к упругому телу и вызывающие в нём изменение размеров и формы, совершают работу Wна соответствующих перемещениях. Одновременно с этим в упругом теле накапливается потенциальная энергия его деформирования U. При статическом нагружении упругих тел потенциальная энергия деформации равна работе внешних сил  . .Это означает, что при статическом нагружении работа внешних сил полностью преобразуется в потенциальную энергию деформации. При разгрузке тела производится работа за счет потенциальной энергии деформации, накопленной телом. Рассмотрим стержень, который растягивается в пределах упругих деформаций на величину Δl (рис. 1.11). Графически зависимость между силой и удлинением представлена на рисунке прямой линией. В процессе нагружения внешняя сила растет от нуля до конечного значения F. Соответственно и удлинение растет от нуля до конечного значения Δl. Этот процесс можно представить как последовательность бесконечно малых приращений удлинения dΔl, вызываемых силой 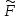 . Следовательно, работа текущей силы . Следовательно, работа текущей силы 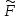 на элементарном перемещении dΔl равна на элементарном перемещении dΔl равна 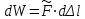 , ,а работа на перемещении Δl  или численно равна площади треугольника ОАС, показанного на рис. 2.11:  . .Эту формулу можно использовать лишь в случаях, когда продольная сила и площадь поперечного сечения постоянны.  Рис. 1.11. Если продольная сила или площадь поперечного сечения изменяются по длине стержня, то потенциальная энергия упругой деформации определяется суммированием значений потенциальной энергии, накапливаемой на элементарном участке 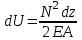 , т.е. , т.е.  . .Для оценки энергоемкости материала определяют удельную потенциальную энергию, накапливаемую в единице объема V 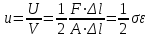 , Дж/м3. , Дж/м3.1.4 Испытания материалов на сжатие Испытания на сжатие дают меньше информации о свойствах материала, чем испытания на растяжение. Тем не менее, они совершенно необходимо для характеристики механических свойств материла. Испытание материалов на сжатие производится на образцах, имеющих вид цилиндров, высота которых не более 1,5 диаметров. Результаты испытаний носят некоторый условный характер из-за наличия сил трения в опорных поверхностях образца. Для бетона, древесины применяют образцы в виде кубиков. Диаграмма сжатия низкоуглеродистой стали Начальный участок диаграммы является прямолинейным – до точки А (рис. 1.12). Угол наклона совпадает с углом наклона аналогичного участка диаграммы растяжения. Поэтому модуль Юнга у стали при растяжении и сжатии считают одинаковым. После точки А диаграмма плавно переходит в кривую, аналогичную диаграмме растяжения. Площадка текучести здесь выражена слабо. При дальнейшем нагружении образец сплющивается и принимает бочкообразную форму. 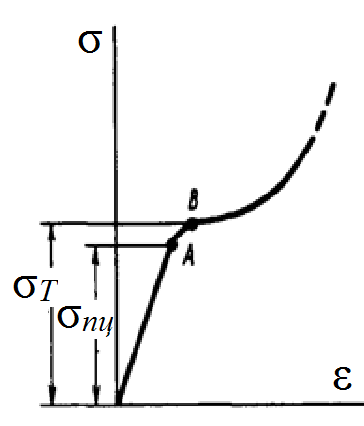    Рис. 1.12. На этом испытание обычно и заканчивается, т.к. образец разрушить не удается, как не удается и определить предел прочности. Значения предела пропорциональности и предела текучести при растяжении и сжатии практически одинаковы. Диаграмма сжатия чугуна очень похожа по форме на диаграмму растяжения (рис. 1.13): с самого начала искривляется и по достижении максимальной нагрузки обрывается. 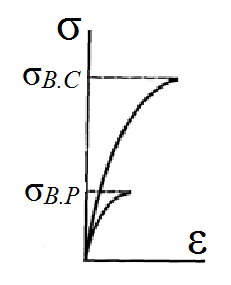 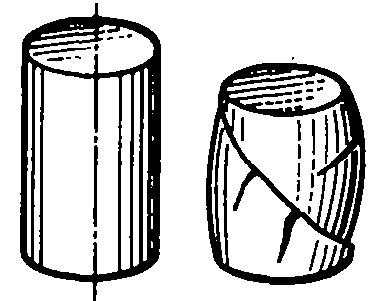 Рис.1.13. Разрушение материала происходит в основном от сдвигов по площадкам с наибольшими касательными напряжениями. Однако на сжатие чугун работает намного лучше, чем на растяжение: для серого чугуна  , , 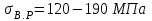 , т.е. в 4 – 5 раз меньше. Предел прочности – это единственная механическая характеристика чугуна, получаемая при испытании на сжатие. , т.е. в 4 – 5 раз меньше. Предел прочности – это единственная механическая характеристика чугуна, получаемая при испытании на сжатие.Большинство хрупких материалов (бетон, камень) разрушаются при сжатии так же, как и чугун, и имеют аналогичную диаграмму. Диаграмма сжатия древесины Представляет интерес испытание древесины – анизотропного, т.е. обладающего различной прочностью в зависимости от направления силы по отношению к направлению волокон, материала. Из диаграммы следует, что при сжатии вдоль волокон (кривая 1 на рис. 1.14) древесина значительно прочнее, чем при сжатии поперек волокон (кривая 2).  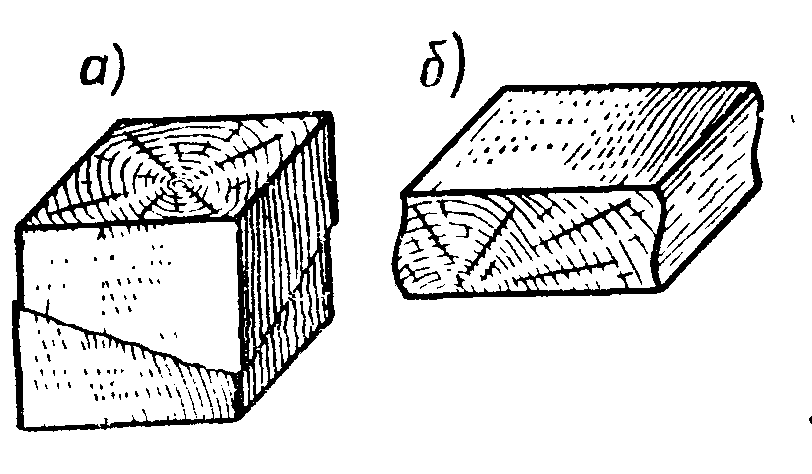 Рис. 1.14. Кривая 1 похожа на кривые сжатия хрупких материалов. Разрушение происходит вследствие сдвига одной части кубика относительно другой (рис.1.15, а). При сжатии поперек волокон древесина не разрушается, а прессуется (рис.1.15, б) Сопротивление древесины сжатию вдоль волокон в 8 – 10 раз больше, чем поперек. 1.5 Измерение твëрдости Распространенным механико-технологическим испытанием является определение твердости. Это обусловлено быстротой и простотой таких испытаний и ценностью получаемой информации: твердость характеризует состояние поверхности материала детали до и после технологической обработки (закалки, азотирования и т.п.), по ней можно судить о величине предела прочности. Под твëрдостью материала подразумевается способность сопротивляться проникновению в него другого, более твëрдого материала (индентора). Количественно это свойство материала измеряется числом твëрдости. Определяемые числа твердости для одной и той же поверхности материала, но разными способами, различны по величине, различны по размерности. F  Рис.1.15 Наиболее распространенный метод испытаний – по Бринелю заключается в том, что в образец вдавливают стальной закаленный шарик диаметра D (рис.1.15) и выдерживают некоторое время под нагрузкой F, в результате чего на поверхности остается отпечаток (лунка) диаметра d. Отношение нагрузки в кН к площади поверхности отпечатка в см2 называется числом твердости по Бринелю 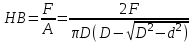 . .Пользуясь числом твердости HB, можно без разрушения образца получить приближенное значение предела прочности некоторых материалов, т.к. существует линейная связь между σВ и HB: 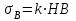 (для малоуглеродистой стали (для малоуглеродистой стали  , для высокопрочной стали , для высокопрочной стали  , для чугуна , для чугуна 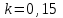 , для алюминиевых сплавов , для алюминиевых сплавов  , для титановых сплавов , для титановых сплавов 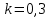 ). ). Существуют и другие методы определения твердости (по Роквеллу, по Кубасову, по Шору, по Виккерсу), которые здесь не рассматриваются. 1.6 Влияние различных факторов на механические характеристики Испытания материалов проводятся при нормальных условиях, т.е. температуре 20ºС, давлении 760 мм рт ст. Однако строительным и машиностроительным конструкциям приходиться работать в различных условиях. Например, при повышенных температурах (конструкции доменных печей, ракетных двигателей и др.) или при пониженных температурах (в условиях Крайнего Севера, вечной мерзлоты или в криогенных установках), при действии радиоактивных, особенно нейтронных, проникающих излучений (ядерные реакторы, парогенераторы и др.). Механические характеристики будут изменяться в зависимости от условий эксплуатации конструкций и сооружений, элементов машин и механизмов. Перечислим основные факторы, влияющие на механические свойства материалов: изменение температуры; термическая обработка; скорость приложения нагрузки; влияние технологических факторов (прокатка, волочение, токарная обработка, обработка роликами и т.п.); радиоактивное облучение; длительность приложения нагрузки, при котором проявляется свойство ползучести, характеризуемое нарастанием деформации во времени при действии постоянной нагрузки. Отметим еще одно явление, характеризуемое медленным уменьшением напряжений в образце при постоянной деформации и называемое релаксацией. В заключение приведем характеристики прочности и пластичности некоторых материалов, применяемых в строительстве (табл.1.1), а также значения упругих постоянных этих материалов (табл.1.2). Таблица 1.1
Таблица 1.2.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
