Да да. Методические указания Расчет волнового сопротивления
 Скачать 125.8 Kb. Скачать 125.8 Kb.
|
|
Расчет вторичных параметров симметричных цепей Методические указания Расчет волнового сопротивления При расчете Zв следует помнить. Что по своей природе волновое сопротивление не зависит от длины кабельной линии и постоянно в любой точке, однако оно существенно зависит от частоты. При постоянном токе волновое сопротивление следует определять из выражения:  , Ом, (1) , Ом, (1)где R0 – сопротивление цепи постоянному току, Ом/км; G0 – проводимость изоляции по постоянному току, См/км; Rиз – сопротивление изоляции, Ом·км. В диапазоне низких частот (f<800Гц) при соотношении параметров 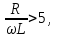 волновое сопротивление равно: волновое сопротивление равно: , Ом. (2) , Ом. (2)В тональном диапазоне частот (f=800Гц) при соотношении параметров  величину волнового сопротивления можно найти по формуле: величину волнового сопротивления можно найти по формуле: , Ом (3) , Ом (3)В области высоких частот (при f>40кГц) волновое сопротивление определяется из выражения (1.11), а на промежуточных частотах – по полной формуле:  , Ом (4) , Ом (4)При решении задач с комплексными числами следует помнить, что комплексным числом z называется выражение:  (5) (5)где a и b – действительные числа; i – так называемая мнимая единица. Величина а называется действительной или вещественной частью (a=Rez), b – мнимой частью числа z (b=Imz). Всякое комплексное число  можно изобразить на плоскости в виде точки A(a, b) с координатами a и b (рис.1). можно изобразить на плоскости в виде точки A(a, b) с координатами a и b (рис.1).Тогда:  , (6) , (6) , (7) , (7) . (8) . (8)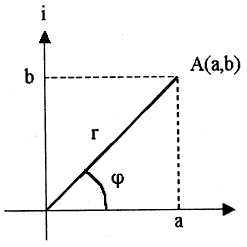 Рис. 1. Изображение комплексного числа Рис. 1. Изображение комплексного числаВыражение 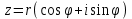 называется тригонометрической формой записи комплексного числа называется тригонометрической формой записи комплексного числа  ; r – называется модулем комплексного числа z, φ – аргументом комплексного числа Z; они обозначаются ; r – называется модулем комплексного числа z, φ – аргументом комплексного числа Z; они обозначаются 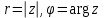 . .Через a и b эти величины выражаются как: 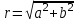 , (9) , (9) , (10) , (10)Причем аргумент комплексного числа φ записывается в виде – (φ+2πk), где k – целое число или 0. Найти значение arctg x можно путем разложения в ряды:  , (11) , (11) , (12) , (12)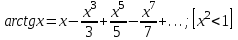 , (13) , (13)Для раскрытия квадратного корня с комплексными числами можно воспользоваться выражениями:  . (14) . (14)Для показательных функций будут справедливы следующие выражения:  ; (15) ; (15)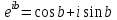 ; (16) ; (16) . (17) . (17)Расчет коэффициента распространения электромагнитной энергии Электромагнитная энергия, распространяясь вдоль линии связи, уменьшается по величине и изменяется по фазе от начала к концу линии. Коэффициент затухания α и коэффициент фазы β в общем виде определяются по формуле расчета коэффициента распространения. Коэффициент распространения γ является комплексной величиной и может быть определен суммой действительной и мнимой ее частей:  , (18) , (18)где  - круговая частота - круговая частота  ; ;R – сопротивление цепи, Ом/км;  - проводимость изоляции цепи, См/км; - проводимость изоляции цепи, См/км;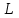 - индуктивность цепи. Гн/км; - индуктивность цепи. Гн/км;С – емкость цепи, Ф/км. При известных значениях тока или напряжения в начале и в конце линии коэффициент распространения можно представить в следующем виде: 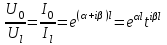 , (19) , (19)где 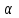 - коэффициент затухания; - коэффициент затухания; - коэффициент фазы. - коэффициент фазы.Действительная часть 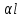 коэффициента распространения показывает уменьшение электромагнитной энергии в конце линии по сравнению с началом и называется собственным затуханием линии: коэффициента распространения показывает уменьшение электромагнитной энергии в конце линии по сравнению с началом и называется собственным затуханием линии: . (20) . (20)Мнимая часть выражения 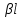 - показывает изменение фазы (угла) при распространении энергии по цепи и называется собственным сдвигом фазы линии: - показывает изменение фазы (угла) при распространении энергии по цепи и называется собственным сдвигом фазы линии: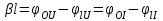 . (21) . (21)Расчет коэффициента затухания Затухание принято оценивать в дицибелах (белах) или неперах. Затухание в 1 Нп – это затухание с такой симметричной цепи, в которой ток или напряжение в начале линии больше по абсолютной величине, чем ток или напряжение в конце в 2,718 раза: 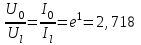 . .Затухание в 1 бел (Б) соответствует снижению мощности по абсолютной величине в 10 раз:  Б, (22) Б, (22)или:  . .Децибел является одной десятой бела:  дБ. (23) дБ. (23)или:  . .То есть, децибел соответствует снижению мощности в 1,26 раза. Для взаимного перевода непер в децибелы необходимо воспользоваться следующими значениями:  , (24) , (24)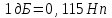 (25) (25)Для определения затухания в определенных частотных областях можно пользоваться упрощенными формулами. При постоянном токе: 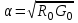 , Нп/км (26) , Нп/км (26)где  - сопротивление цепи постоянному току, Ом/км; - сопротивление цепи постоянному току, Ом/км;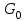 - проводимость изоляции по постоянному току, См/км. - проводимость изоляции по постоянному току, См/км.В диапазоне низких частот (f<800Гц) при соотношении параметров  : :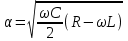 , Нп/км. (27) , Нп/км. (27)В тональном диапазоне частот (f=800Гц) при соотношении параметров 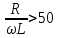 : : , Нп/км. (28) , Нп/км. (28)В областях высоких частот (при f>40кГц), когда 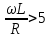 и и 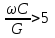 , следует пользоваться формулой (1.12). В этой формуле первый член учитывает потери в металле, а второй – потери в диэлектрике. , следует пользоваться формулой (1.12). В этой формуле первый член учитывает потери в металле, а второй – потери в диэлектрике.Для нахождения затухания на промежуточных частотах следует воспользоваться полным уравнением коэффициента затухания:  , Нп/км. (29) , Нп/км. (29)Коэффициент затухания кабельной цепи при температуре, отличной от 200С, можно найти из формулы: 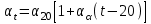 , дБ/км, (30) , дБ/км, (30)где  - коэффициент затухания при температуре 200С, дБ/км; - коэффициент затухания при температуре 200С, дБ/км; - температурный коэффициент затухания, - температурный коэффициент затухания,  , , Таблица 1 Для кабелей МКС - 4 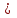 4 4
Расчет коэффициента фазы Коэффициент фазы определяет угол сдвига между током (или напряжением) на протяжении одного километра. Для определения коэффициента фазы в определенных частотных областях также можно пользоваться упрощенными формулами. При постоянном токе: 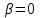 (30) (30)В диапазоне низких частот (f<800Гц) при соотношении параметров  : :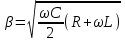 , рад/км. (32) , рад/км. (32)В тональном диапазоне частот (f=800Гц) при соотношении параметров 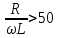 : :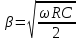 , рад/км. (33) , рад/км. (33)В областях высоких частот (при f>40кГц), когда 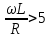 и и 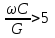 : : , рад/км. (34) , рад/км. (34)Для определения коэффициента фазы на промежуточных частотах следует решить полное уравнение: 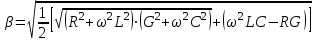 , Нп/км. (35) , Нп/км. (35)Если затухание цепи определяет дальность связи, то коэффициент фазы обуславливает скорость распространения энергии по линии. Расчет скорости распространения энергии Скорость распространения электромагнитной энергии является функцией частоты и фазовой постоянной, которая в свою очередь зависит от первичных параметров линии. В общем виде она определяется по формуле: 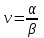 , км/с. (36) , км/с. (36)Для определения скорости в определенных частотных областях следует пользоваться упрощенными формулами. в спектре низких частот (f<800Гц):  , км/с. (37) , км/с. (37)В области высоких частот (при f>40кГц), когда скорость не зависит от частоты и определяется только параметрами кабеля:  , км/с. (38) , км/с. (38)Для расчета скорости движения электромагнитной энергии постоянного тока можно использовать формулу:  , км/с. (39) , км/с. (39)Скорость прохождения постоянного тока по линии составляет примерно 10000км/с, а токи высоких частот движутся со скоростью до 200000 км/с, приближаясь к скорости света (с=300000 км/с). Решение задач Задача 1. Определить минимальное и максимальное значения волнового сопротивления электромагнитной волне, проходящей по симметричной паре кабеля МКСГ 4 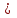 4, если кабель работает с системой передачи К-60. 4, если кабель работает с системой передачи К-60.Решение. Максимальным волновое сопротивление будет на нижних частотах передаваемого сигнала, а минимальным – на верхних частотах. Минимальной и максимальной частотой передаваемого сигнала в аппаратуре К-60 будут соответственно 12 и 252 кГц. Для решения этой задачи воспользуемся формулами для расчета волнового сопротивления в различных частотных областях. Волновое сопротивление на частоте 12 кГц будет определяться по формуле (4), а на частоте 252 кГц – по формуле (1.11). Для расчетов по этим формулам нам необходимо сначала определить первичные параметры симметричной цепи – R, G, L, C на заданных частотах. Воспользуемся ранее представленной методикой расчета первичных параметров в задачах №1-4 (практическое занятие №2). Значение сопротивления на частоте 252 кГц было найдено в задаче №1 (практическое занятие №2). Определим R на частоте 12 кГц. Параметр kr составит для f=12кГц:  . .Значения специальных функций Бесселя F(kr), G(kr), H(kr) находим из табл.4 (практическое занятие №2): F(kr)=0,0217; G(kr) =0,0583; H(kr)=0,0842. Значение потерь на вихревые токи в проводах смежных четверок и в металлической оболочке кабеля для f=12кГц: 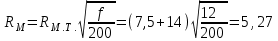 Ом/км. Ом/км.Общее значение сопротивления симметричной пары на частоте 12кГц:  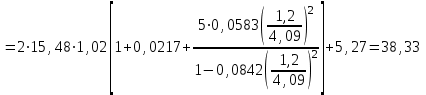 Ом/км; Ом/км;для f=252 кГц (см.задачу №1 практическое занятие №2): 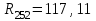 Ом/км. Ом/км.Определим индуктивность L на частотах 252 и 12 кГц (см.задачу №2 практическое занятие №2). Значение kr: для f=252 кГц:  ; ;для f=12 кГц:  . .Значение специальной функции Бесселя Q(kr): для f=252 кГц: Q(kr)=0,455; для f=12 кГц: Q(kr)=0,989. Общее значение индуктивности: для f=252 кГц:   мГн/км; мГн/км;для f=12 кГц: 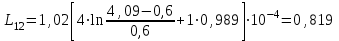 мГн/км. мГн/км.Определим емкость симметричной пары. Значение емкости не зависит от частоты, ее величина для кабеля МКСГ 4 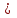 4 была найдена в задаче №3 (практическое занятие №2) С=24,12 нФ/км. 4 была найдена в задаче №3 (практическое занятие №2) С=24,12 нФ/км.Искомые значения проводимости изоляции на частотах 252 и 12 кГц в кабеле МСКГ 4 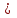 4 были найдены в задаче №4 (практическое занятие №2). Их значения составили: 4 были найдены в задаче №4 (практическое занятие №2). Их значения составили:для f=12 кГц: 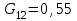 мкСм/км; мкСм/км;для f=252 кГц: 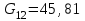 мкСм/км. мкСм/км.Определив все значения первичных параметров, найдем величины волновых сопротивлений. Волновое сопротивление на частоте 12 кГц (формула 4 практическое занятие №2) будет равно: 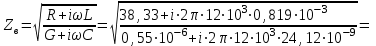  Ом. Ом.Волновое сопротивление на частоте 252 кГц:  Ом. Ом.Ответ: Максимальное волновое сопротивление  Ом (на f=12 кГц); минимальное волновое сопротивление Ом (на f=12 кГц); минимальное волновое сопротивление 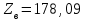 Ом (на f=252 кГц). Ом (на f=252 кГц). |

